基于ANSYS Workbench的某大型氧化铝仓有限元分析

曾 勇

(贵阳铝镁设计研究院有限公司，贵州 贵阳 550081)

0 引 言

目前世界氧化铝、电解铝工业的发展趋势主要表现为在尽可能降低生产成本的同时，最大限度地解决由生产所带来的环境保护问题。采用先进技术，扩大生产规模，节能降耗是实现上述目标的主要手段。因此，氧化铝、电解铝工业所采用的设备越来越向着大型化、自动化、高效化及节能化方的向发展。伴随着单线产能不断增大，对产品氧化铝堆存和输送的要求也越来越高，储量大、投资低、占地少、操作便捷的氧化铝堆存设施的开发设计已迫在眉睫，大型的氧化铝储仓更是其中的关键设备之一。传统的氧化铝仓是按照经验以及简单公式计算结果进行设计的，设计过于保守，这导致了氧化铝仓所采用的钢板厚度过高，大大增加业主费用；该文通过对某工程25 000 t氧化铝仓静态分析和地震反应谱分析，对氧化铝仓等大型设备有限元分析提供参考。

1 氧化铝仓有限元模型及相关参数

氧化铝仓直径为36 m，总高为35 m，氧化铝储仓的整体结构材料是Q235B，其材料属性和力学性能为：密度7.85×103 kg/m3，弹性模量为206 GPa，泊松比为0.3，屈服极限为235 MPa。

氧化铝总容积为34 081 m3，有效容积约为27 265 m3，储存物料为沙状氧化铝(干粉)，物料堆积比重约为9.5 KN/m3，物料密度取1.1 t/m3，氧化铝物料与仓壁间的摩擦系数为0.4，物料内摩擦角：35°～380°，取下限值350，考虑物料为沙土模型时，假设物料为连续介质实体，其力学性能为：弹性模量为8 MPa，泊松比为0.25。

氧化铝仓仓盖采用桁架结构，仓体钢板壁厚采用递减式设计，在满足设计要求的同时可有效减轻设备自重，提高经济性，氧化铝仓有限元模型见图1。

由于氧化铝仓模型较大，单元数量较多，为求得可靠结果，综合考模型求解速度和精度，本文中氧化铝仓采用四面体网格单元，共1 463 628个节点，1 251 960个单元格；网格划分示意图见图2。

图1 氧化铝仓有限元模型Fig.1 Finite element model of alumina bin

图2 氧化铝仓网格划分示意图

2 静态分析

静态分析主要是分析氧化铝仓正常工作时，在恒定荷载和常见可变荷载作用下氧化铝仓的形变情况和应力分布情况。

2.1 恒定荷载

恒定荷载由包括氧化铝仓自重以及附加设备重，可以通过ANSYS Workbench软件自动加载计算，重力加速度取9.8 m/m2

2.2 可变荷载

可变荷载包括贮料荷载、风荷载、雪荷载等

2.2.1 贮料荷载

根据GB50884—2013《钢筒仓技术规范》中的规定，贮料计算高度hn与矩形仓的短边bn之比小于1.5时的钢筒仓为浅仓，该文中的氧化铝仓为浅仓，仓贮料压力见图3。贮料荷载作用在氧化铝仓上的力有2种：①物料对筒壁产生的水平压力Phk；②物料对筒壁产生的竖向摩擦力Pfk。

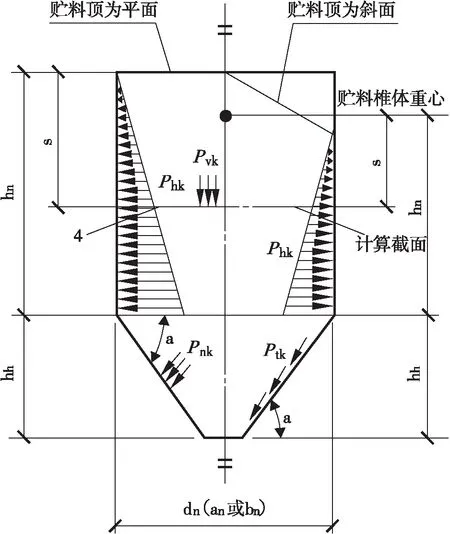
图3 浅仓贮料压力示意图

1)贮料顶面或贮料锥体重心以下距离s处，贮料作用于仓壁单位面积上的水平压力标准值Phk应按公式(1)计算。

Phk=kγs(1)

式中：

Phk——贮料作用于仓壁单位面积上的水平压力标准值(N/mm2)；

γ——贮料的重力密度(N/mm3)；

k——侧压力系数；

s——贮料顶面或贮料锥体重心至所计算截面的距离(mm)。

2)贮料顶面或贮料锥体重心以下距离s处的计算截面以上仓壁单位周长上的总竖向摩擦力标准值应按式(2)计算：

Pfk=μkγs(2)

式中：

Pfk——贮料作用于计算截面以上仓壁单位周长上的总坚向摩擦力标准值(N/mm2)；

μ——贮料与仓壁的摩擦系数。

2.2.2 风荷载

根据《建筑结构荷载规范》GB 50009—2012中的规定，垂直于氧化铝仓表面风荷载标准值应该按照(3)式计算：

wk=βzμsμzw0(3)

式中：

wk——风荷载标准值(kN/m2)；

βz——高度z处的风振系数；

μs——风荷载体型系数；

μz——风压高度变化系数；

w0——基本风压(kN/m2)。

该工程所在地基本风压为0.45 kN/m2，氧化铝仓基础高12 m，设备高35 m。

2.2.3 雪荷载

根据《建筑结构荷载规范》GB 50009—2012中的规定，屋面水平投影上的雪荷载标准值应该按照(4)式计算：

Sk=μrS0(4)

式中：

Sk——雪荷载标准值(kN/m2)；

μr——屋面积雪分布系数；

S0——基本雪压(kN/m2)。

根据工程开工报告得出，该工程所在地基本雪压S0为0.6 kN/m2，结合GB 50009—2012《建筑结构荷载规范》中表7.2.1屋面积雪分布系数和氧化铝仓仓盖角度，取μr的值为0.85。

2.3 分析结果

在贮料荷载、风荷载、雪荷载的共同作用下氧化铝仓的最大应力为180.78 Mpa，最大应力位于氧化铝仓底部边缘，小于材料的屈服极限235 Mpa，满足设计要求；见图4。

最大位移为为6.5 mm，位于氧化铝仓仓顶中间部位，满足设计要求。见图5。

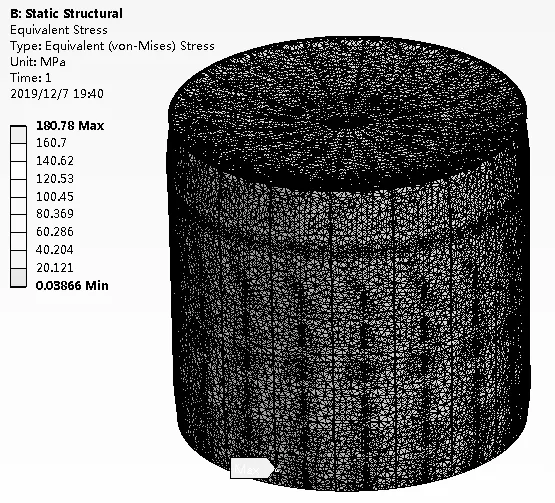
图4 贮料荷载+风荷载+雪荷载作用下的位移云图Fig.4 Displacement fringe under Storage load+wind load+snow load

图5 贮料荷载+风荷载+雪荷载作用下的应力云图

3 模态分析

为防止氧化铝仓在各种工作情况下发生共振，需要对氧化铝仓的模态和振型进行分析计算，该文结合氧化铝实际工作情况，固定氧化铝仓底部进行约束模态分析，氧化铝仓前20阶非零模态频率见图6。

模态分析中，氧化铝仓1～7阶的振型相似，8～9阶振型相似，10～17阶振型相似，18～20阶振型相似，该文具体分析氧化铝仓5阶、9阶、16阶、20阶振型，见图7-10。

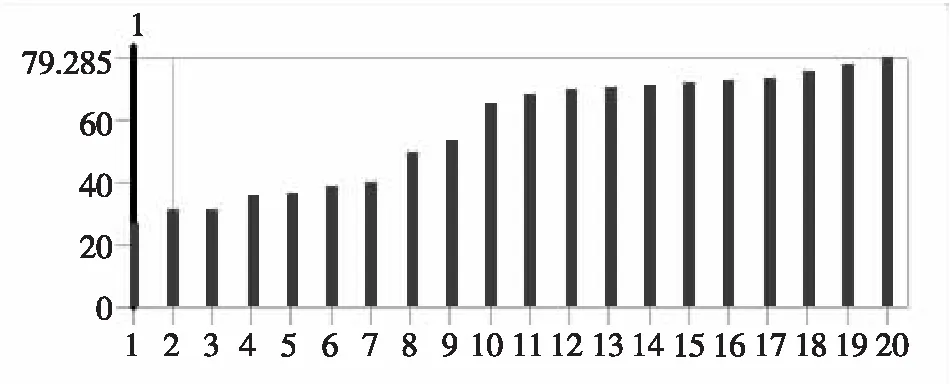
图6 氧化铝仓前20阶非零模态频率

图7 氧化铝仓5阶振型

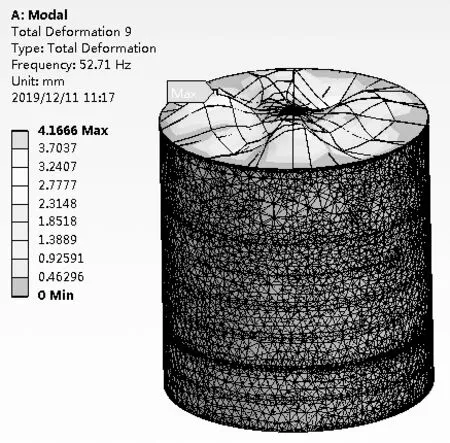
图8 氧化铝仓9阶振型

图9 氧化铝仓16阶振型

图10 氧化铝仓20阶振型

氧化铝仓5阶、9阶、16阶、20阶模态振型特点见表1。

表1 氧化铝仓模态振型特点

4 瞬态动力学分析

4.1 瞬态动力学原理

瞬态动力学分析是研究结构在任意随时间变化的载荷作用下系统的动态响应特性，其原理是将研究对象置于某个符合条件的地震波中，通过数值模拟的方式，对动力学方程进行迭代，得到研究对象在整个时间历程内各物理量的动态响应值，瞬态动力学运动方程如式(5)所示。

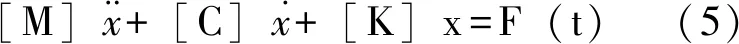
式中：

[M]、[C]、[K]——分别为质量矩阵、阻尼矩阵和刚度矩阵；

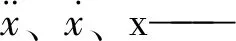
F(t)——变载荷量。

4.2 地震波的选取

结合本工程实际情况考虑。该次分析选取汶川8.0级地震波进行瞬态动力学分析，X轴方向波形图见图11，Z轴方向波形图见图12。

考虑计算等效性，计算截取地震波中加速度最大的时间段(1～3 s)进行分析，分析时间步距为0.02 s，截取地震波波形图见图13。

图11 X轴方向时间—加速度图(横波)

图12 Z轴方向时间—加速度图(纵波)

图13 X、Y轴方向波形图

4.3 计算结果

计算位移云图见图14，应力分布云图见图15。由图14可知，氧化铝仓在地震荷载作用下最大位移为78.597 mm，满足《建筑抗震设计规范》GB 50011—2010最大形变要求，最大位移位于仓盖上。

由图15可知，氧化铝仓在地震荷载作用下最大位应力为207.97 Mpa，小于材料Q235B的屈服极限235 Mpa，结果满足设计要求。

图14 变形云图

图15 应力云图

5 结 语

综上分析，氧化铝仓的设计满足抗震要求。