线性插值在多室箱梁剪力滞后分析中的运用

河北工程大学土木工程学院，河北 邯郸 056000

0 引言

对于薄壁结构来讲，尤其是当结构出现剪力滞后［1］的时候，描述剪力滞变形状态的纵向翘曲位移函数就会变的十分复杂。目前，对于剪力滞后问题，世界各国专家学者的分析方法主要有卡曼理论法、解析理论法等。其中，解析理论法由于其力学推理较为清晰且能够得到问题的闭合解，而被广泛应用于研究当中。例如运用属于解析理论法中的能量变分法进行结构剪力滞问题的分析时，许多学者事先假设出描述剪力滞后状态时的翘曲位移函数，而后基于最小总势能原理建立控制微分方程并予以求解。目前翘曲位移函数的选择有二次抛物线函数，三次或更高幂次的抛物线函数，以及余弦函数、悬链线函数等形式［2］。

综上所述，描述剪力滞变形状态的翘曲位移函数形式的选择，就目前来讲还未形成一个完整统一的理论体系，并且研究学者们对于翘曲函数的修正方法也有所不同，比如是否考虑顶板的自平衡力，是否引入修正系数以描述边界约束影响等。虽然有些研究学者函数形式的选择与有限元分析的结果或者试验结果的对比取得了较为理想的效果，但是目前仍未形成完整、系统的剪力滞后理论分析体系。

1 线性插值函数模拟多室箱梁横截面的纵向翘曲位移

用线性插值函数模拟薄壁多室横截面纵向位移的基本思想是利用横截面各个分段节点处的纵向翘曲位移为基本计算量，除横截面上分段节点外任一点的的纵向翘曲位移利用线性插值函数来描述［3］。选取线性插值函数作为薄壁多室箱梁的纵向翘曲位移函数的话，就能避免翘曲位移函数具体形式的选择对计算结果的影响，并且截面节点划分的越合理，得到的位移函数越真实，即用分段直线逼近和描述结构的实际纵向翘曲位移函数，于此同时切向位移采用了刚周边假定，摒弃薄壁杆件纵向弯曲时的平截面假定，放弃扭转时用于修订纵向翘曲位移的库尔布鲁纳-哈丁修正理论，得到的结果和实际情况会更加接近，为薄壁多室箱梁设计人员提供了一定的参考价值。

2 线性插值函数下位移构成

现就利用线性插值函数来描述任一等截面薄壁结构的薄壁中心线的纵向翘曲位移，如图1 所示：

图1 线性插值示意图

按照图1 写出其具体表达式如下：

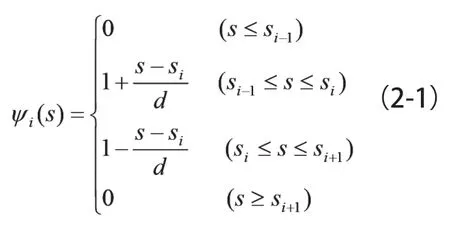
式中：si——沿截面薄壁中心线的第i 点的自然坐标；

d——薄壁结构薄壁中心线相邻自然坐标间的距离，d=si+1-si。

故多室箱梁截面薄壁中心线上任一点的纵向翘曲位移可表示为：

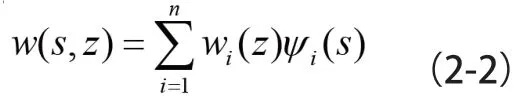
其矩阵表达式为：

或者

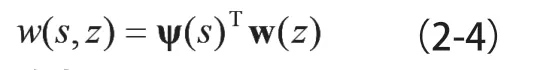
其中：

式中：

有关工作人员基于上述位移场函数可以对薄壁多室箱梁的剪力滞后问题进行分析。

3 结束语

本文基于线性插值函数模拟多室箱梁横截面的纵向位移，对多室箱梁受荷下考虑剪力滞后的位移场进行了推导分析，为薄壁多室箱梁的研究提供了一种思路。