高浓度粗骨料充填料浆抗离析特性及其数学模型
2020-06-17吴凡杨晓炳杨志强高谦
吴凡,杨晓炳,杨志强,2,高谦
(1.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京,100083;2.金川集团股份有限公司,甘肃金昌,737100)
由于充填采矿技术具备安全、经济、环保等优点,越来越多的国家将此项技术应用于矿山开采中[1-4],然而在生产过程中充填料浆离析是至今尚未完全解决的难题。充填料浆在管道输送中,料浆离析导致管道堵塞,影响矿山采充顺序[5-6]。此外,当料浆达到井下采空区后,料浆离析还会造成充填体分层进而导致强度大幅下降,影响矿山安全作业[6-8]。同时,矿山胶结充填料可看成一种低标号流态混凝土[9],研究料浆离析问题在充填采矿、混凝土等领域具有重大的工程意义与理论意义。目前,许多国内外专家学者就此开展了研究。赵国彦等[10]对块石胶结充填料浆中的颗粒离析进行了机理研究;NILI等[11]提出了评价自密实混凝土抗离析性能的新方法;吴爱祥等[12]研究了颗粒级配对粗骨料充填料浆离析的影响规律;TREGGER等[13]研究了混凝土动态离析与塌落度之间关系;史采星等[14]研究了充填料浆离析分层对充填体强度的影响规律;PANESAR等[15]研究了离析对混凝土运输及耐久性能的影响;张云国等[16]通过配合比方法控制自密实轻骨料混凝土抗离析性。然而,与混凝土不同的是,目前关于矿山充填料浆抗离析特性的理论研究较少。高浓度充填是近几十年来充填研究的主要方向[17],以甘肃某镍矿为工程背景,目前该矿棒磨砂无法满足充填骨料的需求,急需矿山周边丰富廉价的掘进废石补充。因此,研究高浓度下废石-棒磨砂混合而成的粗骨料充填料浆的抗离析特性对指导同类型矿山的充填采矿具有重要意义。基于上述分析,本文作者总结初始及临界状态下粗骨料在浆体中的受力情况,提出抗离析特性决定系数,采用泌水率测试实验和料浆流变特性实验对决定系数进行验证,构建抗离析特性数学模型,并运用图像法对模型进行验证,充填体截面骨料分布情况很好地吻合数学模型预测结果,模型可实现对料浆抗离析特性的精准预测,合理指导制备矿山充填料浆。
1 实验
1.1 实验方法
泌水率[18]反映了充填料浆的保水性能,实际上也是浆体的离析特性。将搅拌均匀的充填料浆盛入量杯,测定浆体质量,并换算出其中清水质量;静置60min后,用合理的泌水工具将清水析出,并测定其质量,一般取3次测试结果平均值,泌水率M的计算公式如下:
式中:M为浆体泌水率,%;W为泌出清水质量,g;m为原浆体质量,g;Cw为料浆质量分数,%。
流变特性实验选用美国Brookfield公司生产的R/S型软固体流变测试仪,并配备V40-20型桨式转子测定充填料浆的屈服应力。
1.2 实验材料
实验所用的粗骨料由废石和棒磨砂按不同质量比混合均匀而成,两者均来自甘肃某镍矿,前者为井下掘进废石经颚式破碎机破碎后的废石,后者为戈壁集料经棒磨机加工后的棒磨砂,骨料形状及级配曲线如图1所示。胶结料为42.5硅酸盐水泥,实验用水为室内自来水。实验原材料的力学性能参数如表1所示。
1.3 实验方案
综合各方面因素,确定采用废棒比(废石与棒磨砂的质量比)、砂灰比(骨料与水泥的质量比)和料浆质量分数作为实验影响因素,测定不同浆体的泌水率与屈服应力,实验方案如表2所示。
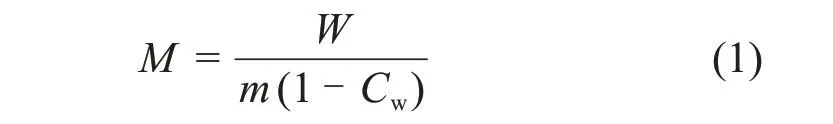
2 粗骨料受力特征分析
2.1 粗骨料初始离析力学模型

图1 骨料形状与级配曲线Fig.1 Shape and grading curves of aggregates
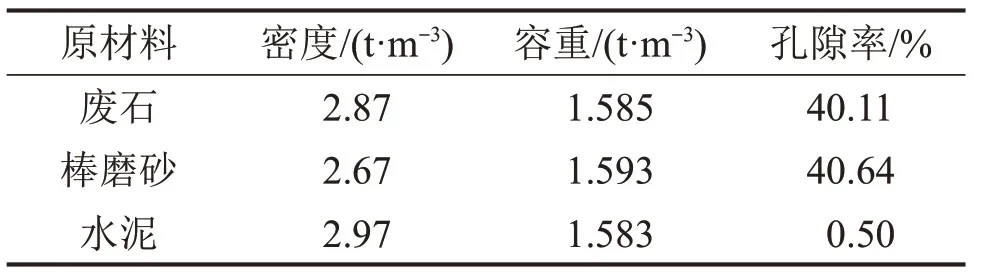
表1 实验原材料参数Table1 Parameters of experimental raw materials
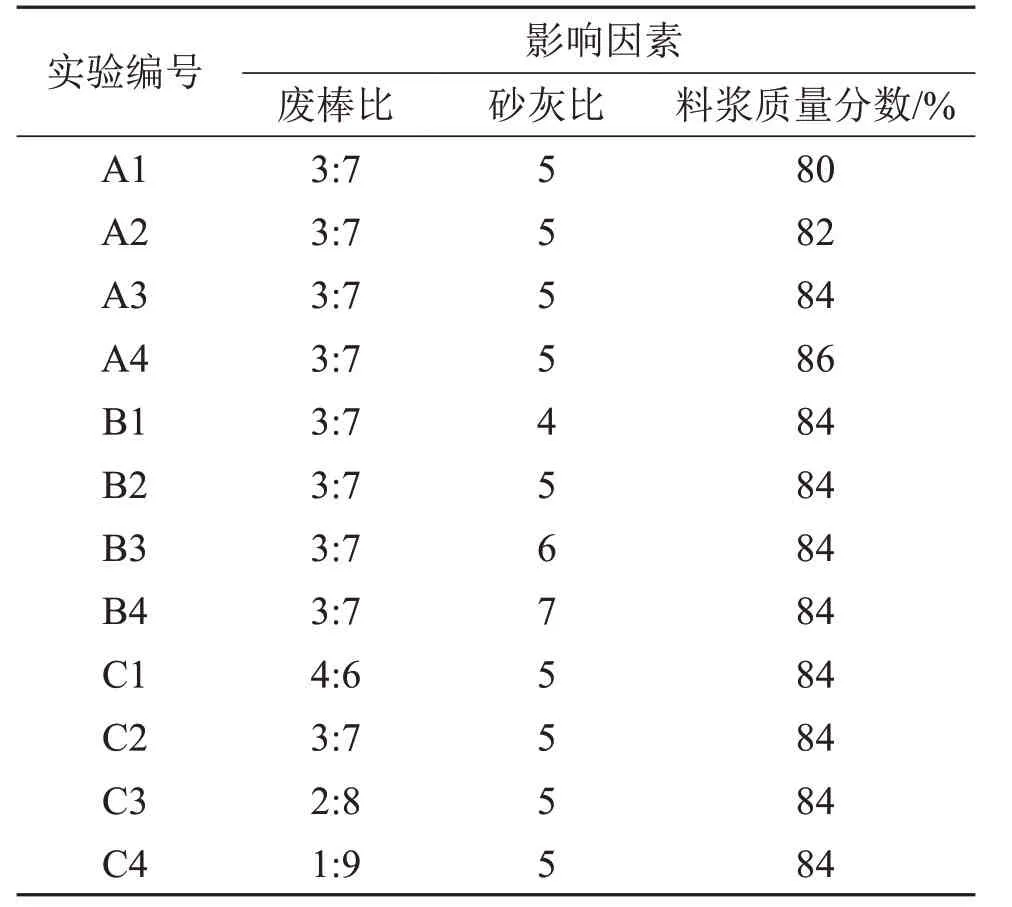
表2 实验影响因素水平Table2 Level of experimental in fluencing factors
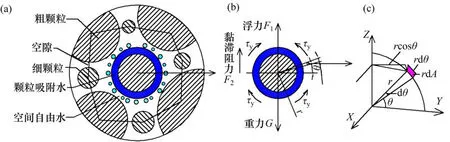
粗骨料充填料浆沉降离析可理解为由于固体颗粒受力不平衡发生固液分层与离析的现象,其实质在于浆体中未形成稳定的空间絮网结构[6,19]。浆体由固体颗粒、空间自由水和颗粒吸附水组成,假设料浆具有良好的均质性,粗骨料为标准圆形状且互不接触。通过分析粗骨料在其絮网结构中的受力状态,建立粗骨料抗离析受力模型。在新拌充填料浆中,初始条件下的粗骨料受到重力G、浮力F1和黏滞阻力F2的共同作用[20-22],其受力分析如图2所示。
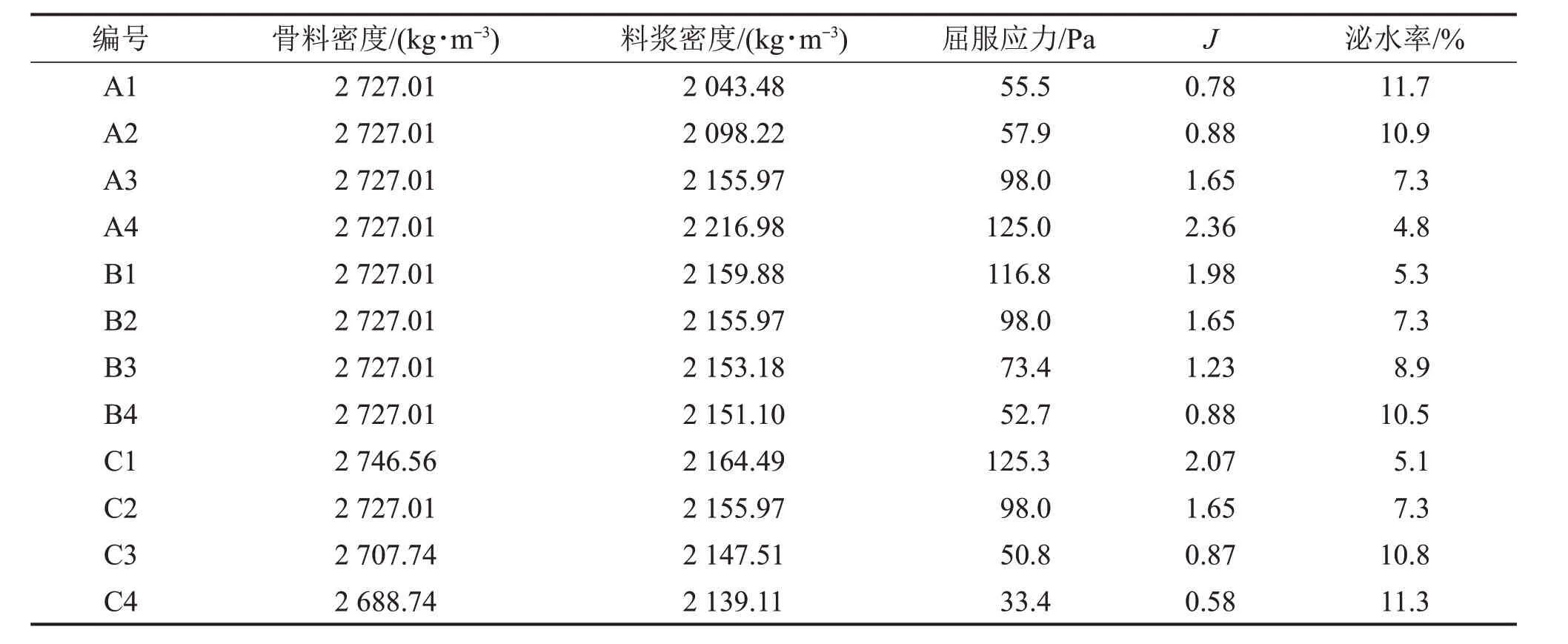
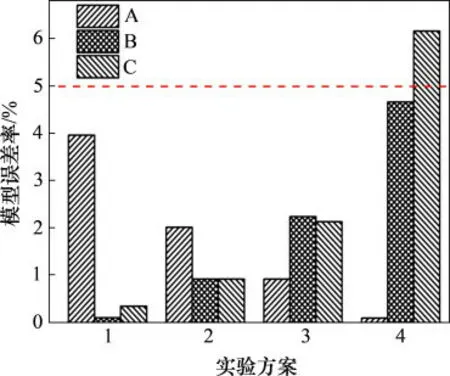
由图2可见:当F2≥G-F1时,粗骨料所受合力≥0且垂直向上,不易发生离析;反之,当F2 黏滞阻力F2来自屈服应力τy在颗粒表面的作用,可表示为 式中:Cs为颗粒形状系数,长方形颗粒取0.6~0.7,扁平形颗粒取0.4~0.6,结合图2所示粗骨料的大颗粒介于两者之间,确定本研究Cs为0.6;A为颗粒的最大截面面积,m2。假设粗骨料与水平方向成θ角处的微分面积为dA,则其对应微元体的黏滞阻力F2在垂直方向上的分力为 对式(4)进行积分可得到1/4的粗骨料的黏滞阻力,进而获得充填料浆中的粗骨料所受黏滞阻力为 粗骨料所受重力G与浮力F1计算式为 式中:ρa为粗骨料的密度,t/m3;ρs为充填料浆的密度,t/m3;g为重力加速度,m/s2;d为粗骨料颗粒直径,m。 联立式(2),(5)与(6),得到初始状态下具备良好抗离析特性的粗骨料充填料浆的理论条件为 图2 粗骨料初始受力分析Fig.2 Initial forces analysis of coarse aggregate 粗骨料充填料浆在管道输送过程中,浆体处于运动状态,内部固体颗粒的受力情况更为复杂,不同于新拌充填料浆的初始状态。与粗骨料初始受力分析相比,临界离析条件下的粗骨料除受到自身重力G、浮力F1和黏滞阻力F2外,还受到左上方和右上方粗骨料的作用力Fcosβ和Fsinβ,其受力分析如图3所示。 图3 粗骨料形临界受力分析Fig.3 Critical forces analysis of coarse aggregate 由图3可见:在临界离析条件下,粗骨料所受到的合力为 因此,在临界条件下,粗骨料充填料浆具备良好抗离析特性的力学条件为 联立式(9),(5)与(6),得到临界状态下具备良好抗离析特性的粗骨料充填料浆的理论条件为 粗骨料初始与临界离析力学模型表明,充填料浆的屈服应力越大,粗骨料与料浆的密度差越小以及粗骨料颗粒的粒径越小,料浆越不容易发生离析。由于临界条件下的粗骨料还受到两侧骨料的作用力,导致粗骨料更易发生离析,料浆不易具备基本的抗离析特性。 文献[20]表明,对于包含多种尺寸颗粒的充填料浆,较最小粒径或平均粒径而言,由最大粒径得到的离析判定值与离析率拟合度最高,能够准确预测抗离析性能,因此,选取粗骨料最大粒径对抗离析特性进行研究。为模拟工业管道输送中粗骨料离析的实际情况与提高抗离析特性表征结果的准确性,基于粗骨料临界离析力学模型,构建抗离析特性决定系数(J),表示为 由理论分析可知,当J>1时,粗骨料不易发生沉降,粗骨料充填料浆具备良好的抗离析特性,反之粗骨料充填料浆不具备抗离析特性。 文献[23]表明,充填料浆的密度可按料浆配合比计算,因此,料浆密度为 式中:G1,G2,G3和G4分别为废石、棒磨砂、水泥和水的质量,t;ρ1,ρ2,ρ3和ρ4分别为对应原材料的密度,t/m3。 粗骨料由废石和棒磨砂按比例混合而成,参照式(12),得到粗骨料密度为 由第2.1节的分析可知Cs=0.6,由图2可知粗骨料dmax=15mm,测定各实验组的屈服应力与泌水率,联立式(11),(12)与(13)计算J,实验结果如表3所示。 由表3可知:随着A1~A4组料浆质量分数的增加,J增加,泌水率减小,提高料浆的抗离析特性;随着B1~B4组砂灰比的增加或C1~C4组废棒比的减小,J减小,泌水率增加,降低料浆的抗离析特性。 为进一步分析理论表征结果与实验结果间的匹配关系,对抗离析特性决定系数与泌水率之间的关系拟合,回归方程为 复相关系数R2=0.972>0.95,回归效果佳。 图4所示为抗离析特性决定系数与泌水率的拟合结果。 由图4可见:A3,B2与C2实验组由于实验方案相同,出现坐标点重合现象;随着J增加,泌水率呈线性减小趋势;料浆是否离析存在分界点,分界点位置J为1,对应泌水率为10%;当充填料浆抗离析特性差、抗离析特性良好、抗离析特性优良时,J分别在0.4~1.0,1.0~1.8和1.8~2.5范围内波动,泌水率分别在12.70%~10.09%,10.09%~6.61%和6.61%~3.57%范围内波动。因此,提高J有利于减小料浆的泌水率,增强料浆抗离析特性,但大幅提高J不利于料浆在管道中的输送,增加充填成本。基于上述分析,可最终得到适合甘肃省某镍矿工程应用的粗骨料充填料浆具备抗离析特性的J范围为1.0~1.8,对应泌水率范围为10.09%~6.61%。值得一提的是,在实际应用中若无法获取料浆特性相关参数的情况下,可直接用泌水率来确定料浆抗离析特性。 为进一步研究抗离析特性与实验影响因素之间的关系,由式(11)可知,J取决于料浆屈服应力τy、粗骨料密度ρa和料浆密度ρs等参数,同时,这些参数又与废棒比、砂灰比和料浆质量分数等实验影响因素相关。 表3 各实验组J与泌水率计算结果Table3 Calculation results of J and bleeding rate of each experimental group 图4 J与泌水率的关系Fig.4 Relationship between J and bleeding rate 为了便于数据处理,将实验方案中的废棒比转化为废石在废石与棒磨砂混合而成的粗骨料中的占比,对表3中的屈服应力τy与各实验方案中的废棒比、砂灰比和料浆质量分数进行多元回归拟合,回归方程为 式中:Fs为废石在废石与棒磨砂混合而成的粗骨料中的占比;B为砂灰比;复相关系数R2=0.959>0.95,显著性系数F=62.972,回归效果佳。 考虑粗骨料与实验影响因素的关系,对式(13)进行化简,得到粗骨料密度为 考虑充填料浆与实验影响因素的关系,对式(12)进行化简,得到料浆密度为: 将式(15),(16)和(17)代入式(11)中,得到抗离析特性数学模型为 将各实验方案代入数学模型中,利用模型计算结果与实验结果计算模型误差率,结果如图5所示。 图5 模型误差率Fig.5 Error rate ofmodel 由图5可见:各实验组模型误差率基本不超过5%,模型平均误差率为2.05%,满足精度要求;A4实验组模型误差率最小(0.10%),C4实验组模型误差率最大(6.17%);随着A1~A4组料浆质量分数的增加,模型误差率减小;随着B1~B4组砂灰比的增加或C1~C4组废棒比的减小,模型误差率增大。 为进一步验证抗离析特性数学模型的准确性,从图像细观尺度观察粗骨料在充填料浆中的离析情况,与模型计算结果进行对比分析。由于A3,B2与C2实验组的材料配比相同,选取A3组为参照组,同时需要考虑废棒比、砂灰比和料浆质量分数对料浆离析的影响,故选取A1,B1与C1组为对比组。按照材料配比制备充填料浆,将配制好的料浆倒入长×宽×高为7.07 cm×7.07 cm×7.07 cm的立方体试模中,静置3 d后拆模,用刀具从底部中线位置沿着立方体高的方向将充填体试样平均切割成两半,使用高清数码相机观察被切割截面粗骨料的分布情况。充填体试块切割截面骨料分布如图6所示,抗离析特性数学模型计算结果如表4所示。 图6 充填体试块切割截面骨料分布Fig.6 Aggregate distribution in cutting section of filling test block 表4 模型J计算结果Table4 Calculating results of model J 由图6和表4可知:A3组模型J为1.59,骨料基本均匀分布在充填体试块切割截面上,具有良好的抗离析特性;与A3组相比,A1组料浆质量分数减小,模型J降为0.63,骨料集中于切割截面中下部,出现了明显的离析分界线,料浆抗离析特性变差;与A3组相比,B1组砂灰比减小,模型J增至1.97,砂灰比的减小使得粗骨料减少,骨料均匀分布在切割截面中,优化了料浆抗离析特性;与A3组相比,C1组废棒比增大,模型J增至2.11,废棒比的增大使得充填浆体中的废石增多,骨料在切割截面上的分布更为均匀,优化了料浆抗离析特性;随着A1,A3,B1和C1这4组的模型J依次递增,骨料分布由集中于切割截面中下部变为基本均匀分布进而转变为均匀分布,充填料浆抗离析特性由差变为良好进而转变为优良。 1)根据粗骨料在充填料浆中初始与临界离析状态下的力学模型,得到了高浓度粗骨料充填料浆抗离析特性决定系数时充填料浆具备良好的抗离析特性。 2)对抗离析特性决定系数与泌水率进行拟合分析结果表明,随着决定系数J增加,泌水率M呈线性减小趋势;判定料浆离析分界点的J为1,M为10%;充填料浆抗离析特性差、良好以及优良时,J分别在0.4~1.0,1.0~1.8和1.8~2.5范围内波动,M分别在12.70%~10.09%,10.09%~6.61%和6.61%~3.57%范围内波动。 3)从抗离析特性决定系数出发,提出用废棒比、砂灰比和料浆质量分数量化表征屈服应力、骨料密度和料浆密度,进而构建了抗离析特性数学模型。各实验组模型误差率基本小于5%,平均误差率为2.05%,满足精度要求,可实现对粗骨料充填料浆抗离析特性的准确预测。 4)从图像细观尺度分析了充填体切割截面骨料分布与抗离析特性模型预测结果的关系,改变废棒比、砂灰比或料浆质量分数等影响因素引起的切割截面骨料分布的改变,与模型预测J变化规律吻合。综上可得,抗离析特性数学模型可靠准确。

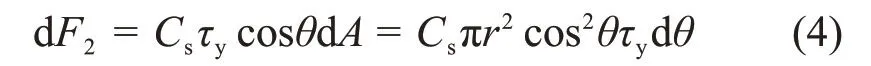
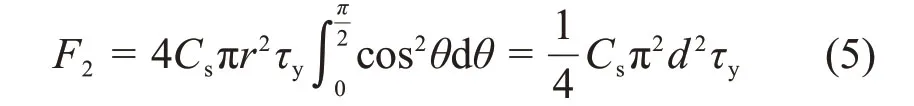
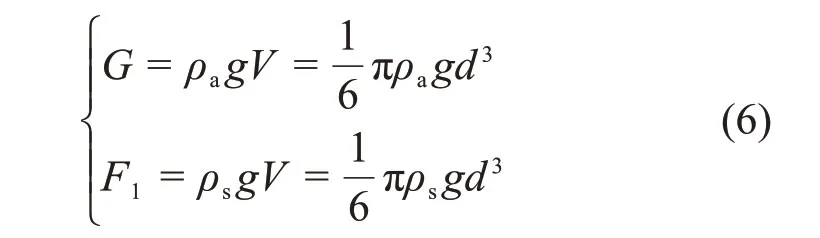

2.2 粗骨料临界离析力学模型


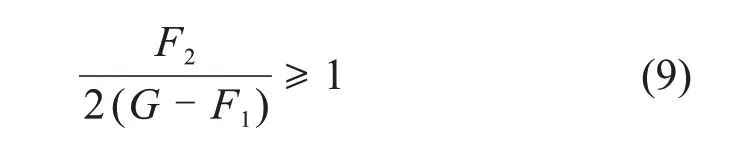
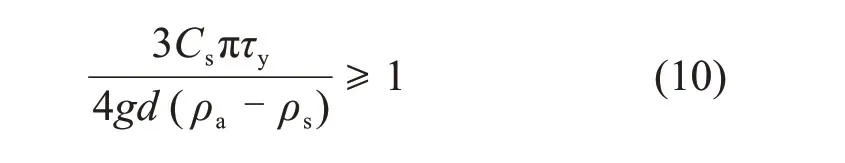
2.3 抗离析特性决定系数
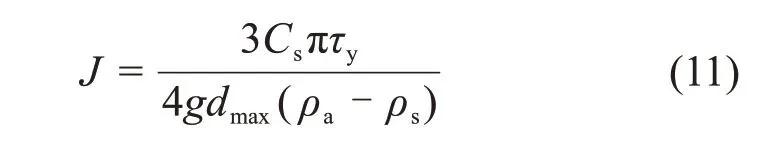
3 结果与分析
3.1 实验结果
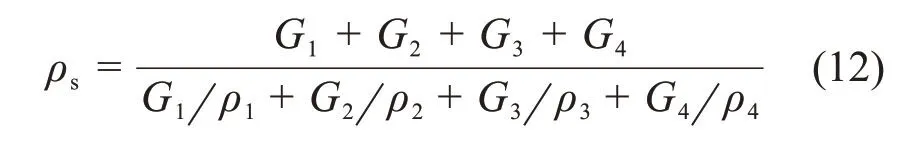
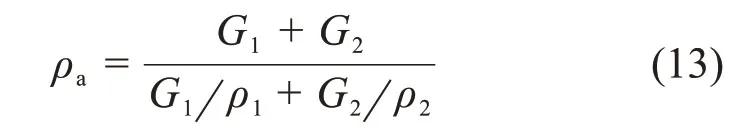
3.2 拟合分析
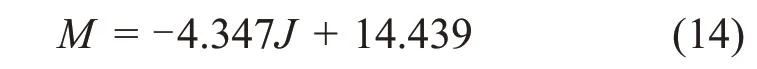
4 抗离析特性数学模型
4.1 模型建立

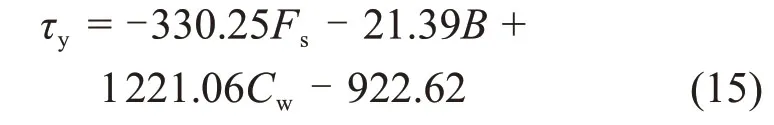
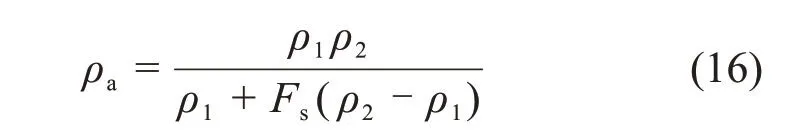
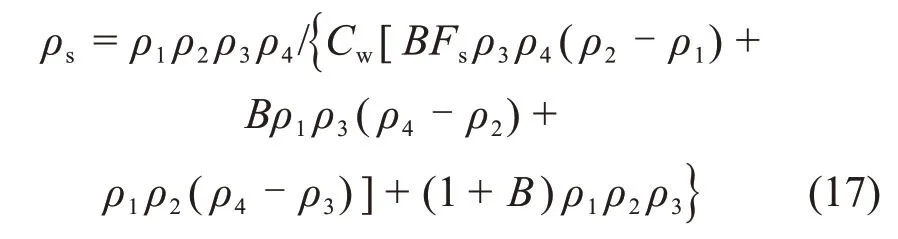
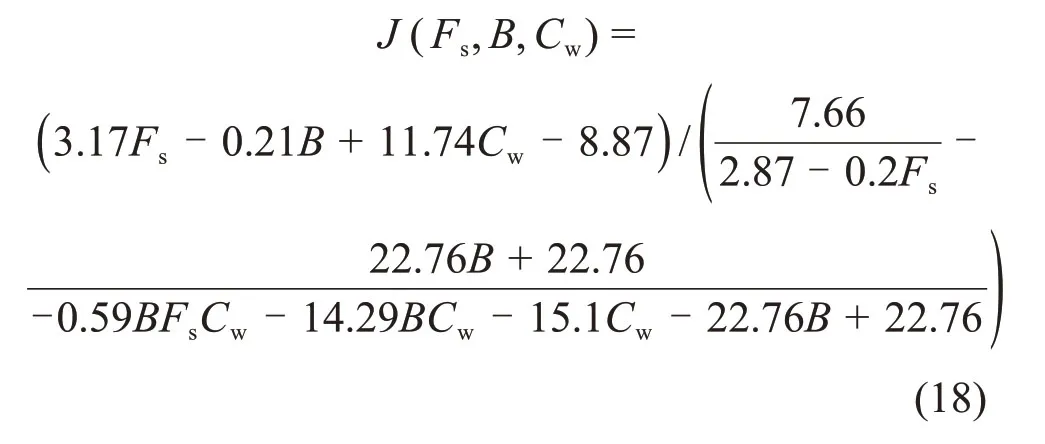
4.2 实例验证


5 结论
