一种试验与仿真联合的阻尼车轮降噪效果评价方法
2020-06-17赵延垒韩健徐圣辉朱自未覃才肖新标
赵延垒,韩健,徐圣辉,朱自未,覃才,肖新标
(1.西南交通大学牵引动力国家重点实验室,四川成都,610031;2.中车青岛四方机车车辆股份有限公司,山东青岛,266000)

图1 意大利Syope阻尼车轮[6]Fig.1 Syope wheels on ETR train[6]
1 现有评价方法及其不足
一般而言,轮轨噪声控制研究往往遵循以下原则:首先运用预测模型进行仿真,然后在实验室进行试验,最后在运营线路上进行现场测试。而在以往的研究中大都将仿真预测、实验室测试以及线路测试分开,各自有着独立的降噪效果评价体系。模型仿真预测[9-11]一般以轮轨辐射声功率级为评价指标;实验室测试一般在半消音室利用麦克风阵列对车轮进行辐射声功率采集[12],其评价指标按照标准ISO3745[13]来测定车轮的辐射声功率级;线路声学测试一般在车外采集噪声,现阶段国际标准ISO3095[14]测量位置定义为距轨道7.5m或者25.0m,评价指标为噪声等效连续声压级。
在现场测试中研究人员逐渐发现[6-7],在实验室利用落球冲击作为激励测试得到的单个阻尼车轮降噪量往往大于线路测试结果,也就是说,考虑车轮噪声占轮轨噪声绝对主导时的理想情况,相对实际线路测试得到的车外噪声而言高估了阻尼措施的降噪效果。试验测试车轮为自由悬挂状态,低频范围内激发的噪声占比较大,实际线路运行为轮轨接触状态,车轮辐射噪声以高频为主,线路运行时车轮声源或传播路径可能不再占据主导地位。根据多声源降噪原则,有效的噪声控制措施应该对2种声源同时控制,当轨道噪声为主要声源时,即使车轮噪声得到了有效降低,但对总声级的影响并不大。考虑实际线路测试情况,高速列车车外实测噪声为气动噪声、车轮噪声、钢轨噪声以及齿轮箱等其他结构产生噪声的叠加,评价体系为声压级,而半消声室的车轮测试一般为自由悬挂状态单个车轮,评价体系为声功率级,两者有所差异,不能直接比较。而TWINS模型中[15]将轮对简化为点声源,钢轨低频简化为点源,高频简化为线声源,在简化计算过程中,部分误差也进一步导致两者的评价差异。
但同时,结合实验室测试的声辐射结果可以合理评估低噪声车轮的降噪性能,具体分析阻尼车轮在车轮辐射噪声显著频段的降噪能力,尤其是在对降噪措施进行优化设计或者相关改进时,落球激励测试的噪声辐射结果是仿真分析的重要数据参考来源,也是作为线路运行安装之前安装必要的试验手段。因此,需要合理评估车轮声辐射试验和仿真值,将两者结合具体分析阻尼车轮的降噪性能以及线路适用性。
2 试验与仿真联合评价方法
考虑低噪声车轮的实际生产周期,实验室测试条件相对容易满足,而线路测试则需要各方面的相关协调并且耗费人力物力较大,并且无法满足所有线路运行状况的测试要求。若可以使用实验室测试的车轮模态数据,结合现有的轮轨噪声预测模型对不同运行工况下的轮轨噪声进行仿真预测,则可以大幅降低低噪声车轮的研发成本以及缩短研发周期。为此,本文提出一种实验室测试和数值仿真结合的研究分析方法,具体如图2所示。
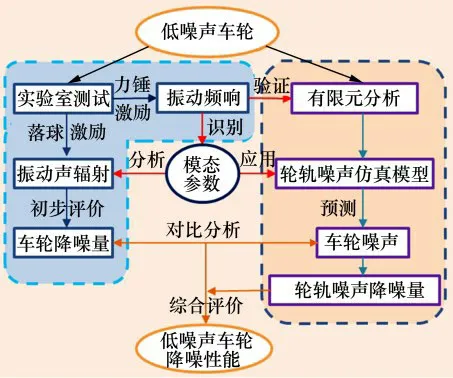
图2 试验与仿真联合方法Fig.2 Research method of testing and simulation
以低噪声技术中的约束阻尼车轮为例,利用半消声室内力锤敲击测试方法获取的车轮振动频响结果和有限元模型计算的频响仿真结果进行对比验证其有效性。通过参数识别方法获取车轮模态参数,并将模态阻尼比应用于验证过的车轮有限元模型中预测分析线路运行条件下的轮轨噪声降噪量,并结合实验室测试的车轮降噪量综合评价阻尼车轮减振降噪性能。结合阻尼车轮线路运行下实测噪声验证该联合方法的有效性。与以往的阻尼车轮研究方法相比较,联合仿真方法可以综合评析阻尼车轮的降噪效果,为高速列车轮轨噪声控制的阻尼车轮技术的改进优化提供相关指导和依据。不过该方法依然存在如下简化之处:1)阻尼车轮的减振效果以阻尼比来量化,可能无法有效仿真需要考虑其静力学作用的阻尼车轮,例如安装动力吸振器的阻尼车轮;2)车轮运行过程中由于钢轨耦合而产生的附加阻尼效应未考虑,本文假定阻尼措施所增加的阻尼远大于滚动阻尼以及车轮材料阻尼。
1934年,美国著名学者杜威在《我们如何思维》中创造性提出了“反思性教学”理念,随后便引起了学术界的广泛重视。唐纳德·舍恩在《反思性实践者》中首次进行了反思性教学实践,并引发了世界各国的教学改革热潮。上世纪80年代,美国、澳大利亚、加拿大等发达国家先后进行了大量反思性教学实践活动,各国学术界也对反思性教学理论进行了深入研究。上世纪90年代,我国正式引入了反思性教学理论,并将其作为教学改革的重要指导。沃丽思(1991)在《反思性教学理念在外语教师培训中的运用》中详细剖析了教育专业化反思模式,为外语教师专业化发展中反思性教育理念的运用提供了重要指导。
3 试验测试与分析
在实际工程应用中,车轮阻尼材料的实际参数可能由于材料加工、环境温度等外界因素使得其与初始设置参数有误差,因此,在测试条件允许的情况下,合理的方法是通过试验测试获得其实际模态阻尼比,有效减小阻尼模型设置的仿真误差,从而可以更好地进行轮轨噪声预测。同时结合实验室测试的振动频响结果验证仿真模型的有效性,实验室车轮噪声测试结果和线路运行预测结果共同分析阻尼车轮的降噪性能。
3.1 模态频响测试
为了获取高铁参考车轮(未安装阻尼措施)以及阻尼车轮(安装约束阻尼板)的模态频率以及模态阻尼比等试验参数,在半消声室内,对自由悬挂状态下安装约束阻尼板前后的高铁车轮进行力锤敲击频响测试。高铁车轮力锤敲击测试安装和测试图如图3所示。
在模态分析实验中,将车轮弹性悬挂于悬臂梁上近似模拟自由状态,其中,振动测点1和振动测点2布置在辐板位置;振动测点3布置在轮辋侧面;振动测点4布置在踏面位置。采用锤击法敲击测试,分别激励车轮名义滚动圆和轮辋位置,每个测点锤击3次,结果取平均值,通过频响函数可以获取车轮的固有频率和对应的模态阻尼比。其中,模态阻尼比的计算方法分为频域和时域法[16],本文通过实验室模态测试利用频域法(半功率带宽法)获取不同车轮模态下的车轮阻尼比。

图3 高铁车轮安装和测试图Fig.3 Test photographs of damped wheel
图4所示为阻尼车轮典型振动测点的频响函数及相干系数结果图。其中加速度参考量为1.0m/s2。
结合不同测点的频响函数获取车轮的模态参数,表1所示为6 000 Hz内参考车轮和阻尼车轮的固有频率以及模态阻尼比。
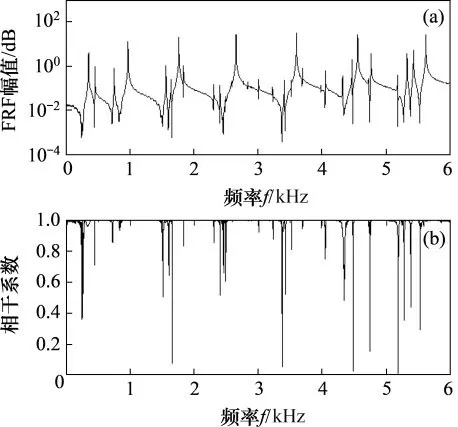
图4 车轮频响函数结果Fig.4 Test results of wheel response function
由表1可见:车轮辐板两侧敷设约束阻尼板可显著提高车轮的模态阻尼比,在增设约束阻尼板的高铁车轮中,最大的阻尼比增量可达4 842%,即其在原有模态阻尼比的基础上增加近48倍,对应的是参考车轮4 470 Hz附近的车轮模态。在800~3 500Hz轮轨噪声显著频率区段,增设约束阻尼板,其对车轮的模态阻尼比提高作用显著,由此可推测阻尼车轮具有较好的降噪效果;高频区段的模态阻尼比增量要比中低频的高,可推测阻尼车轮对高频噪声会有更好的抑制效果。此外,参考车轮和阻尼车轮的固有频率相对变化在3%以内变化,说明约束阻尼板对车轮固有频率影响很小,几乎不改变车轮的固有频率,故安装约束阻尼板的车轮模态振型可近似由参考车轮模态结果代替。
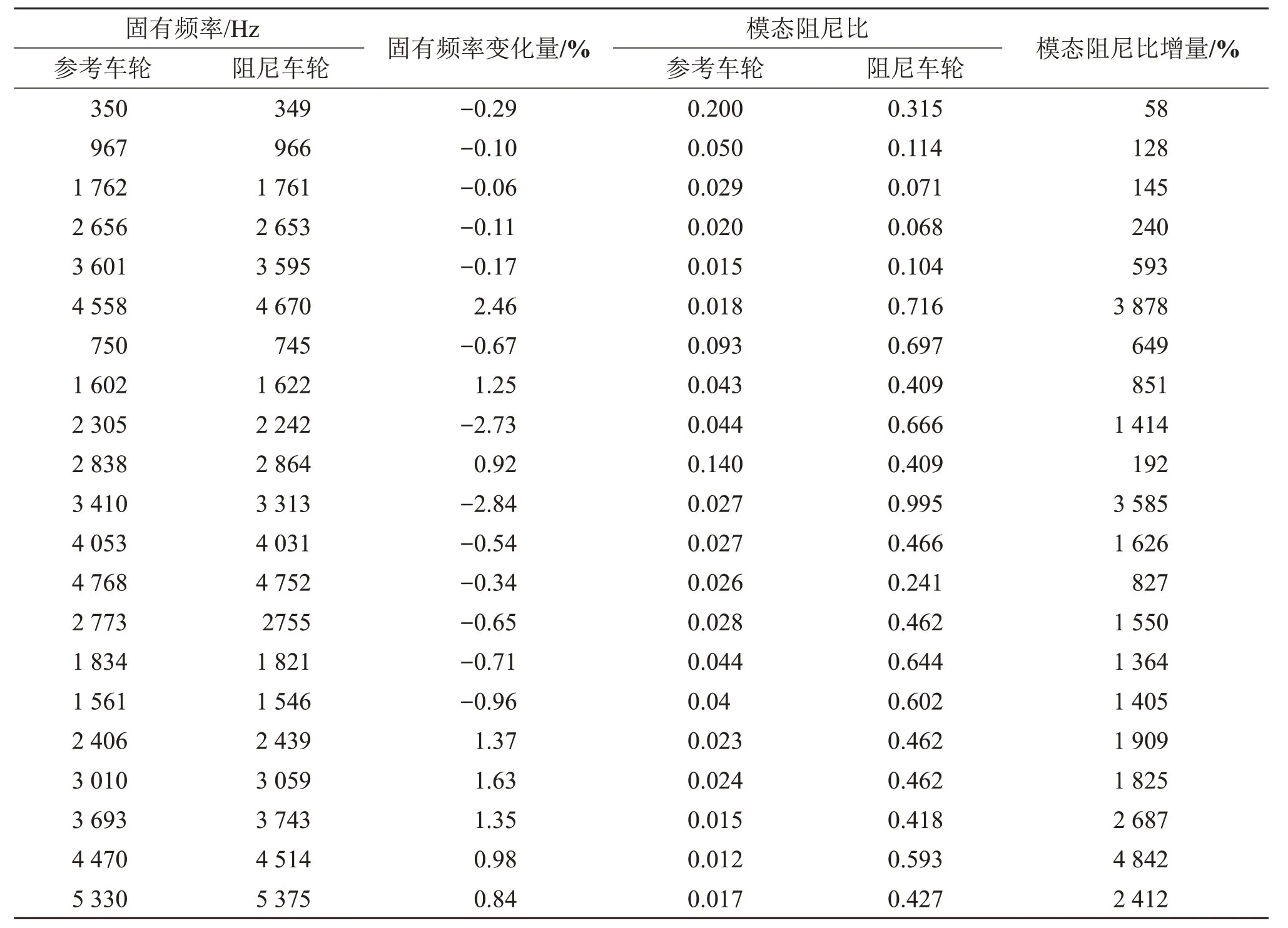
表1 参考车轮和阻尼车轮的固有频率及模态阻尼比Table1 Modal frequency and modal damping ratios of damped wheel and undamped wheel
3.2 车轮噪声测试
在半消声室内,采用落球激励分别激励自由悬挂状态下的参考车轮以及阻尼车轮,试验测试图如图5所示。试验中使用弹性绳使车轮处于自由悬挂状态,为使每次测试的激励输入尽量一致,激励方式选用特制的落球工装使得直径为2.5 cm的钢球从相同高度沿着光滑轨滑落撞击在车轮名义滚动圆和轮辋位置,落球激励位置分别设在踏面和轮缘处。

图5 阻尼车轮声辐射测试Fig.5 Sound radiation test of damped wheels
测试重复3次,结果取平均值。声功率级的基准参考量为10~12W,表2所示为参考车轮和阻尼车轮在径向和轴向落球激励条件下4 s内的总辐射声功率级以及阻尼车轮的降噪效果。
从表2可以看出:在径向激励下,阻尼车轮降噪效果为15.5 dB;在轴向激励下,阻尼车轮降噪效果为10.5 dB。总体来看,阻尼车轮均具有良好的降噪效果,在轴向激励下体现更加明显。
结合声功率频谱特性分析造成声功率总值差异的具体原因。图6所示为参考车轮和阻尼车轮在自由悬挂状态下,径向和轴向落球激励条件下的声功率级的1/3倍频程频谱特性。
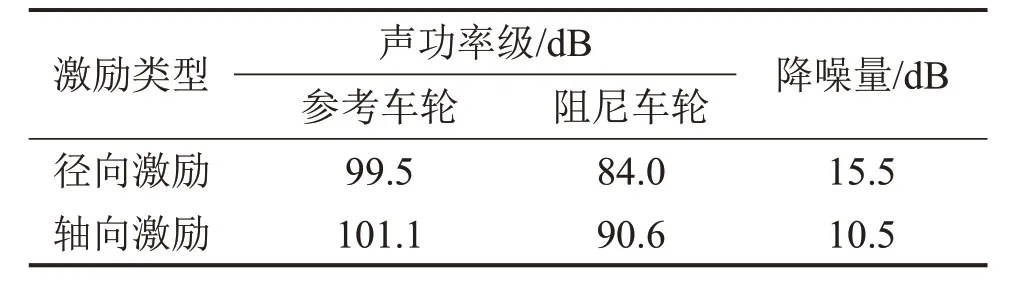
表2 阻尼车轮全频段降噪量Table2 Noise reduction of damped wheel
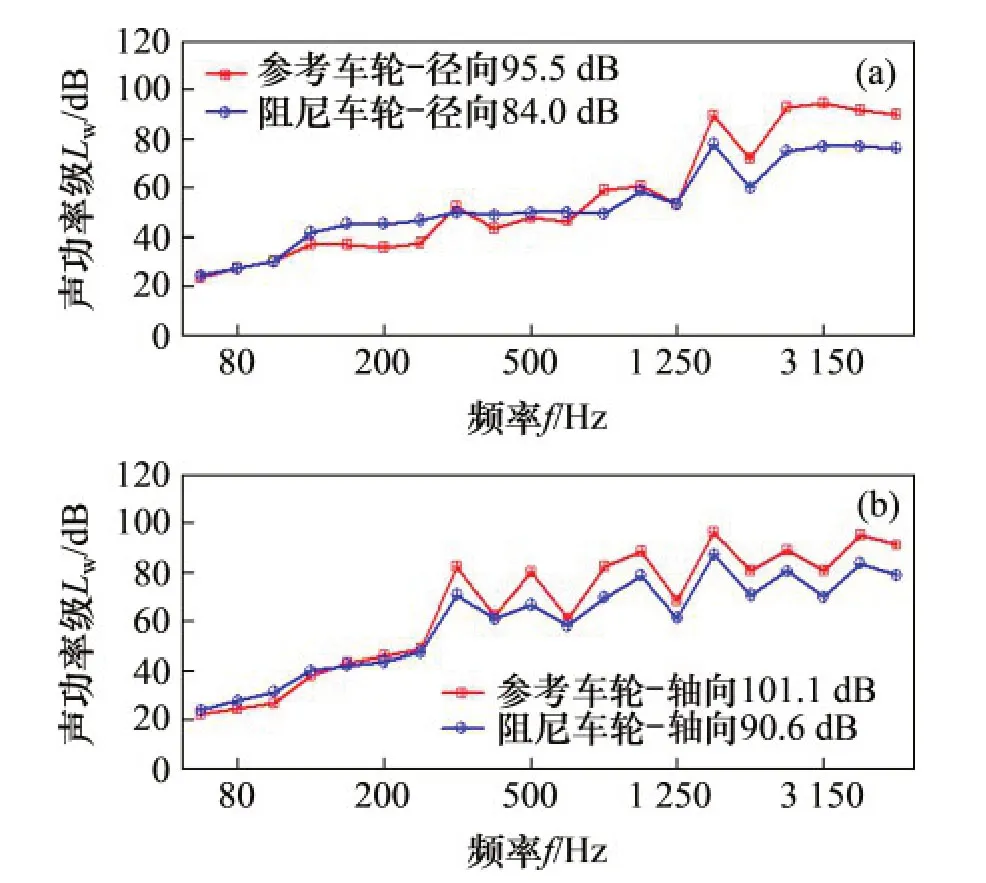
图6 车轮声辐射1/3倍频程频谱特性Fig.6 Sound radiation of 1/3 frequency characteristics
由图6可见:阻尼车轮在高频范围内的降噪效果明显;在径向激励条件下,在参考车轮辐射噪声显著的中心频率为1 600,2 000,2 500,3 150,4 000和5 000Hz时,阻尼车轮辐射声功率级分别降低了11.8,11.9,18.0,18.0,15.1和13.9 dB,总辐射声功率级降低15.5 dB;在轴向激励条件下,在参考车轮辐射噪声显著的中心频率为1 600,2 000,2 500,3 150,4 000和5 000 Hz时,阻尼车轮辐射声功率级分别降低了9.2,10.0,8.4,10.5,11.9和12.3 dB,总辐射声功率级降低10.5 dB。由上述分析可知:在自由悬挂状态下,阻尼车轮对径向激励和轴向激励条件下的辐射噪声有着很好的抑制作用,其中,在轴向激励条件下,阻尼车轮的降噪显著区域对应的频率范围更宽,中高频区域具有更好的降噪效果。
4 数值仿真与分析
参考目前应用广泛的轮轨噪声预测频域模型[17-21],基于二维有限元和边界元方法计算轮轨噪声预测模型计算车轮以及钢轨的振动声辐射特性,其中,轮轨粗糙度激励输入为高铁线路实测车轮钢轨粗糙度,钢轨为标准60轨。
4.1 车轮振动模型
车轮为轮廓面比较复杂的实体结构,因此,本文采用有限元方法进行车轮的振动仿真分析。而本文研究的参考车轮为轴对称结构,采用有限元软件的2D轴对称单元对车轮建模仿真可以同时兼顾模型计算的准确性以及计算速度的运算要求,为此,本文采用参考车轮的有限元模型,如图7所示。
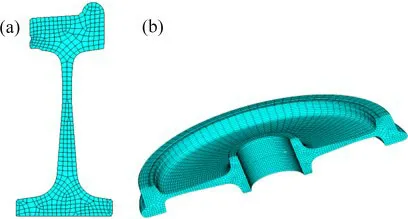
图7 参考车轮有限元模型Fig.7 Wheel FEM model
利用有限元分析软件对车轮模型进行模态分析,分别计算其在自由约束状态下的固有频率与振型。由前面测试模态结果可知,安装约束阻尼板的车轮模态振型可近似由参考车轮模态结果代替,因此,本文仅建立参考车轮的有限元模型,在计算阻尼车轮时,按照参考车轮的模态振型数据以及实测的阻尼车轮模态阻尼比计算其轮轨噪声。
基于模态叠加法计算车轮名义滚动圆处的车轮导纳,为了验证模型的有效性,结合实验室力锤敲击法测试结果对比分析。图8所示为自由状态下,车轮的名义滚动圆处径向加速度导纳的仿真值和试验值对比。
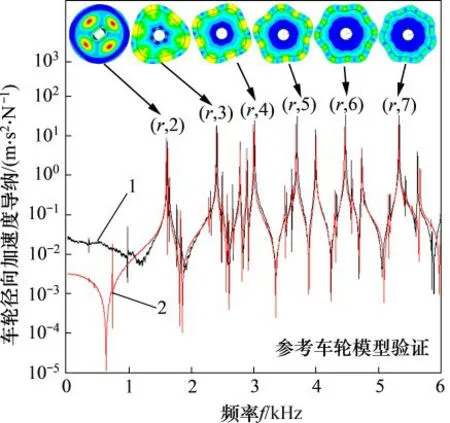
图8 车轮模型验证Fig.8 Verification of wheel model
由图8可知:车轮径向加速度导纳主要峰值频率在1 500 Hz以上,几个峰值频率分别为1 600,2 403,3 003,3 680,4 453和5 308Hz,主要对应车轮的径向模态(1,2),(r,3),(r,4),(r,5),(r,6)和(r,7)。在自由状态下,由模态叠加法计算得到的车轮振动响应与力锤锤击试验结果相比,峰值和幅值吻合较好,因此,本文所建立的车轮有限元模型可以用于轮轨噪声仿真计算。
进行阻尼车轮线路运行降噪仿真时,利用已验证的车轮有限元计算模型,结合车轮实际运行状态下的边界条件等实际情况,在车轮轮毂孔施加约束条件,约束下的模态结果用于轮轨振动噪声计算。表3所示为约束状态下车轮模态频率计算结果。其中,(r,1)和(r,2)模态频率变换较大,结合模态振型可知,约束轮毂孔有效改变了其模态振型,如图9所示。此模态的模态阻尼比也会随着边界条件的改变而改变,但从图9可以看出,该频率区段振动对整体振动影响较小,而其他模态振型、模态频率和自由状态与同节圆节径下的模态振型和模态频率近似,因此,可以近似将两状态下车轮的阻尼比等同,忽略边界条件改变所带来的阻尼比差异。
4.2 轮轨声辐射模型
轮轨噪声计算模型参考THOMPSON等[19-20]所构建的TWINS模型,大量现场测试结果验证了该计算模型的准确性,此处仅给出计算思路。
列车运行时受车轮和钢轨表面不平顺和粗糙度的相对位移激励,激发轮轨动力作用,进而引起车轮、钢轨和轨道结构振动并向周围环境辐射噪声。在工程上,结构振动的辐射声功率可以用下式表示:

表3 车轮模态仿真计算结果Table3 Model calculation results of wheel
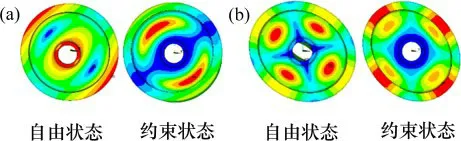
图9 自由状态和约束状态差异模态对比Fig.9 Contrast differential modes of free state and constrained state
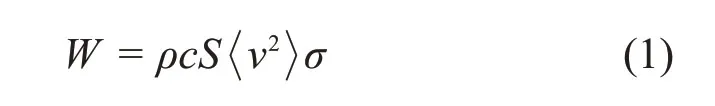
式中:ρ为空气密度;c为空气中的声速;S为结构声辐射总面积;
根据我国高铁某线路实测轮轨踏面粗糙度谱计算轮轨动态作用力,在轮轨动态力作用下采用模态叠加法结合车轮仿真模型以及实测的车轮模态阻尼比计算车轮的振动响应,使用离散支撑的Timoshenko梁模型[22]计算钢轨和轨枕振动响应。将碎石道床简化为离散的复刚度弹簧,轨枕采用集中质量简化,先求解钢轨离散点的振动响应,再结合简化模型计算轨枕振动响应,利用约束状态下的车轮仿真模型以及实测的车轮模态阻尼比计算车轮表面振动能量,叠加声辐射效率计算车轮、钢轨以及轨枕的辐射声功率,最终叠加为总的轮轨噪声。计算模型如图10所示,实测车轮钢轨粗糙度如图11所示。结合标准ISO3095[14]附录的波数域的轮轨表面粗糙度数据进行对比。其中粗糙度参考量为1.0mm,波长采用1/3倍频程方式表示。
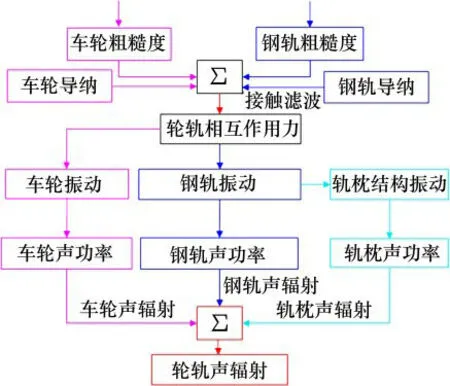
图10 轮轨声辐射模型Fig.10 Wheel/rail acoustic radiation model
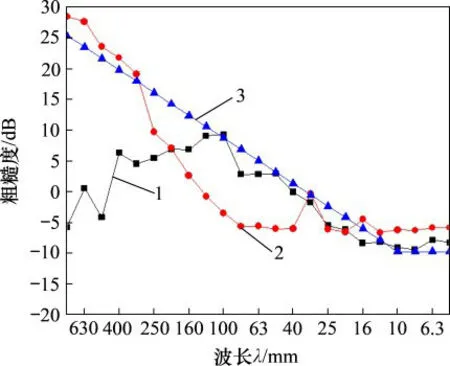
图11 轮轨粗糙度Fig.11 Wheel/rail roughness
为了了解在线路运行情况下车轮、钢轨、轨枕各部分的声贡献,设置计算运行速度工况为220 km/h。图12所示为参考车轮以及阻尼车轮在线路运行条件下的轮轨噪声声功率级。
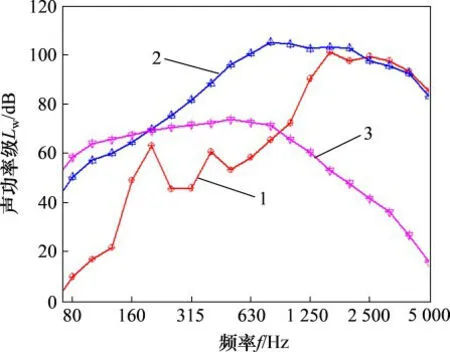
图12 参考车轮运行状态轮轨噪声特性Fig.12 Noise characteristicsof undamped wheel and rail in running state
由图12可以看出:当列车运行于实际线路时,车轮、钢轨以及轨枕对轮轨噪声的贡献量存在明显差异;在0~2 500 Hz频率范围的轮轨噪声中轨道声辐射起主导作用,在2 500~5 000Hz频率范围轮轨噪声中车轮噪声大于钢轨噪声;在0~800 Hz频率范围内,轨枕噪声大于车轮噪声、小于钢轨噪声,在800 Hz以上的频率范围内,轨枕噪声的声功率级最小。总体而言,在列车高速运行时,车轮噪声和钢轨噪声起主要作用,在进行轮轨噪声减振降噪时,需要尽可能地兼顾车轮钢轨的振动特性,统筹兼顾,合理配置相关降噪方案,从而有效降低轮轨滚动噪声。
图13所示为参考车轮和阻尼车轮的车轮噪声和轮轨噪声仿真预测结果,其中轮轨噪声为车轮噪声、钢轨噪声以及轨枕噪声预测结果的能量叠加。
由图13可知:当阻尼车轮以220 km/h速度运行时,阻尼车轮在高频频段内有明显的降噪效果。其中,参考车轮、阻尼车轮的车轮噪声声功率级分别为105.8 dB和101.7 dB,降噪量为4.1 dB;运行状态下的轮轨总噪声分别为112.8 dB和111.8 dB,降噪量为1.0 dB。结合实验室测试降噪效果和阻尼车轮降噪性能,并考虑到实验室测试和实际线路运行时激励力不同,为横向对比降噪效果,消除激励力影响,引入降噪性能比参数ε,定义为降噪量与参考车轮声功率的比值,即
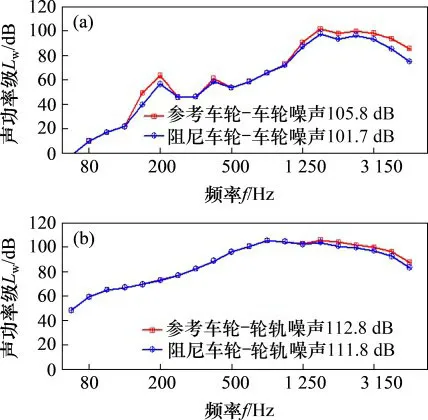
图13 车轮噪声以及轮轨噪声声功率预测结果Fig.13 Prediction results of wheel-railnoise sound power
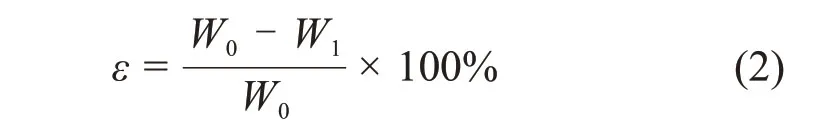
式中:W0为参考车轮声功率;W1为阻尼车轮声功率;W0-W1为车轮降噪量。
由此可以计算出实验室测试降噪性能比为97%,线路运行车轮降噪性能比为61%,线路运行轮轨噪声降噪性能比为21%。综合评价结果证明安装约束阻尼板可以有效降低轮轨辐射噪声。
5 方法验证
考虑轮轨噪声仿真计算值分别为车轮和钢轨的声功率级,现场实测为车外声压级,本文将车轮简化为移动的点声源,钢轨低频部分视为点声源,钢轨高频部分视为线声源,忽略单极点声源对声场的指向性,不考虑多普勒效应;另外,由于声传感器采集点距离钢轨为3.3m远小于钢轨模型计算长度,且意大利阻尼车轮[6]现场测试轨道为有砟轨道,考虑其测试区间粗糙度较小,未达到ISO3095[14]打磨限值,与本文实测粗糙度之间的差异可忽略。同时,考虑地面吸声系数较大,故在声压级转换时忽略地面反射声以及轨枕二次噪声。
利用轮轨噪声预测模型计算阻尼车轮声功率降噪情况,结合计算路旁噪声测点与文献[6]现场测试结果进行对比,结果如图14所示。
由图14可知:当阻尼车轮以速度220 km/h运行时,阻尼车轮具有明显的降噪效果,车外噪声点降噪量为3.0 dB。其中,参考车轮实测值和预测值吻合较好,阻尼车轮的频谱规律与实测结果相似,但由于文献中阻尼参数以及车轮阻尼层尺寸与本文所使用的不一致,预测的阻尼车轮降噪效果比实际线路测试效果略差,但总体而言,本文预测结果与文献[6]中结果相符,验证了本文提出的联合仿真方法的可行性。
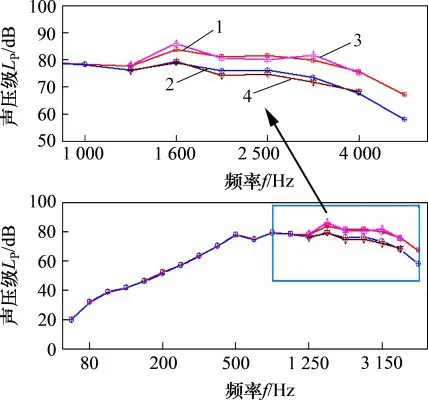
图14 路旁噪声仿真和实测声压级对比Fig.14 Comparison between simulation and measurement of sound pressure spectra
6 结论
1)以往实验室测试时一般会高估阻尼车轮的降噪性能,而实际线路运行测试耗费大量人力物力,并且无法满足所有线路运行状况的测试要求,本文提出的联合仿真评价方法可以有效降低低噪声车轮的研发成本以及缩短研发周期。
2)以约束阻尼车轮为例,结合试验测试分析以及数值仿真对阻尼车轮降噪效果进行评价分析,在实验室测试的阻尼车轮在径向激励和轴向激励下,声功率级降噪量分别为15.5 dB和10.5 dB;利用数值仿真分析其车轮声功率在速度220 km/h时声功率级降噪量为4.1 dB。实验室测试降噪性能比为97%,线路运行车轮降噪性能比为61%,线路运行轮轨降噪性能比为21%。综合评价分析证明安装阻尼车轮对轮轨辐射噪声有着很好的抑制作用。
3)基于试验和仿真联合方法预测的阻尼车轮声功率级结果,利用声源简化方法,仿真预测车外路旁噪声声压级降噪量为3.0 dB,轮轨噪声预测结果与约束阻尼车轮实际线路试验结果频谱特性相符,证明所提出的方法是合理的且能满足现场评价分析应用需求。本文所提出的评价方法和研究结果可为高速列车减振降噪技术的发展提供科学参考与依据。
