连续排水边界条件下饱和软土一维大变形固结解析解

2020-06-17江文豪詹良通杨策

中南大学学报（自然科学版） 2020年5期

江文豪，詹良通，杨策

(1.浙江大学岩土工程研究所，浙江杭州，310058；2.浙江大学软弱土与环境土工教育部重点实验室，浙江杭州，310058；3.杭州绿农环境工程有限公司，浙江杭州，310000)

自20世纪20年代土体一维固结理论建立以来[1]，国内外学者通过对其基本假定进行修正，不断发展和完善了一维固结理论。土体的一维大变形固结理论起始于20世纪中期，GIBSON等[2]以孔隙比为变量推导得到了土体一维大变形固结的控制方程，但由于控制方程的高度非线性，无法直接求得解析解。POSKITT[3]基于GIBSON大变形固结理论，孔隙比e与土体的有效应力和渗透系数kv采用线性的e-lgσ'和e-lgkv关系描述土体固结过程中压缩性和渗透性的变化，利用摄动法得到了土体一维大变形固结解析解。GIBSON等[4]假定GIBSON大变形固结理论控制方程中的固结系数与重力系数均为常数，采用有限差分法分析了不同条件下土体一维大变形固结性状。MCVAY等[5]基于GIBSON大变形固结理论，并假定中土体固结过程压缩性关系与渗透性关系均满足指数变化规律，对土体的固结性状进行了讨论。谢新宇等[6-7]基于连续介质力学的基本原理，建立了以位移为控制变量的一维大变形固结方程，并研究了渗透系数变化对土体一维大变形固结性状的影响。张继发等[8]根据混合物理论，推导了土体一维大应变固结方程，并应用李群变换的方法获得了某些特定条件下控制方程的隐式解答。XIE等[9]通过假定体积压缩系数为常数，渗透系数与孔隙比的平方成正比，得到了饱和软土一维大变形固结的解析解。吴健等[10]基于GIBSON大变形理论的控制方程，考虑土体的渗透系数和孔隙比、有效应力和孔隙比之间的非线性关系，分析了不同渗透指数与压缩指数的比值下软土的固结特性。李传勋等[11-12]考虑非DARCY渗流定律，在拉格朗日坐标系下建立了以超孔隙水压力为变量的土体一维大应变固结方程，并运用有限差分法进行求解。但以上关于一维大变形固结理论的研究对象主要集中于土体压缩特性和渗透特性，对土体排水边界随时间发展过程的研究还不够深入。传统排水边界条件主要包括完全透水边界和完全不透水边界。此外，也有学者对半透水边界条件进行了研究。早在20世纪40年代，GRAY[13]对半透水边界进行了研究。SCHIFFMAN等[14]研究了半透水边界条件下，渗透系数与体积压缩系数变化对土体固结的影响。谢康和等[15-16]将半透水边界的运用推广到层状地基，分析了层状土在半透水边界下的一维固结特性。李西斌等[17]研究了双面半透水边界饱和土体在循环荷载作用下的黏弹性固结问题，得到了半透水边界下黏弹性地基的解析解。然而，传统排水边界与时间无关，存在孔压突变为零的问题，无法反映土体排水边界随着固结过程发展的变化情况。半透水边界虽然体现了透水边界的变化过程，但其物理意义并不明确，无法定量描述界面排水能力[18]。针对上述排水边界问题存在的不足，梅国雄等[19-20]提出了考虑边界孔压随时间指数衰减的连续排水边界条件，并给出了相应的瞬时加载条件下一维固结方程的理论解答。宗梦繁等[21]对连续排水边界条件下土体非线性固结性状进行了研究；童立红等[22]对连续排水边界条件下黏弹性地基的固结性状进行了分析。但以上基于连续排水边界的固结研究中均未对土体的大变形固结性状进行研究，而实际工程中常常会遇到土体的大变形固结问题。基于此，本文作者首先基于XIE等[9]饱和软土一维大变形固结的假设，通过引入连续排水边界条件研究饱和软土的一维大变形固结问题，并得到连续排水边界下饱和软土一维大变形固结的解析解。然后，通过退化解析解和有限差分数值解对比分析，对该解析解的正确性进行了验证。最后，基于所得解析解，分析界面参数及荷载参数对土体一维大变形固结性状的影响。

1 基本问题

本文采用XIE等[9]提出的饱和软土一维大变形固结问题中的基本假定，饱和软土的渗透系数kv与孔隙比e有如下关系式：

式中：kv0和e0分别为土体的初始渗透系数和初始孔隙比。

在饱和软土固结过程中，假定土体的体积压缩系数mv1保持不变[9]，即

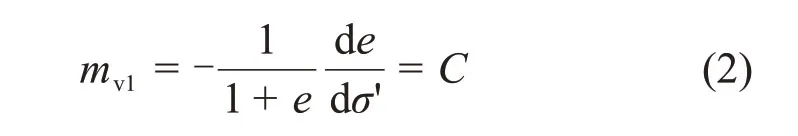
式中：σ'为土体的有效应力；C为常数。

根据上述假定，土体的固结系数Cv可表示为

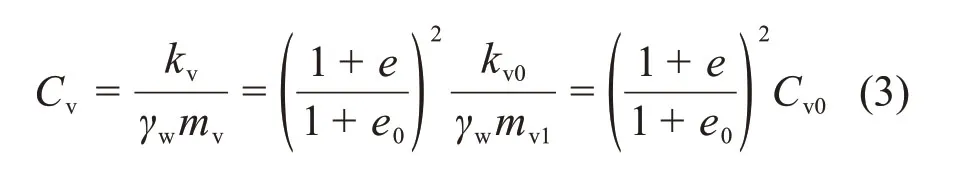
式中：Cv0为土体的初始固结系数；γw为水的重度；mv为体积压缩系数。

在大变形固结过程中，由于土体会产生较大的变形，因此通常采用拉格朗日坐标系进行度量。根据上述假定，可推导得到饱和软土固结过程中以超孔隙水压力u为变量在拉格朗日坐标下的控制方程[9]为

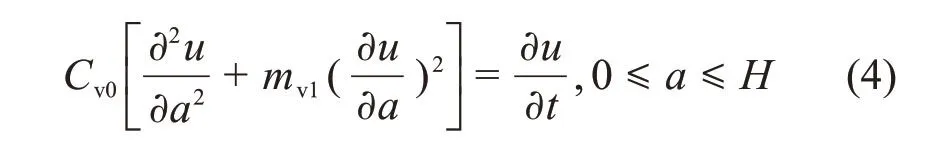
式中：a为拉格朗日坐标系下的竖向方向；t为时间；H为饱和土体的初始厚度。

根据梅国雄等[19-20]提出的连续排水条件，该一维大变形固结方程的求解条件如下。

初始条件：

式中：qu为瞬时施加的均布荷载。

边界条件：

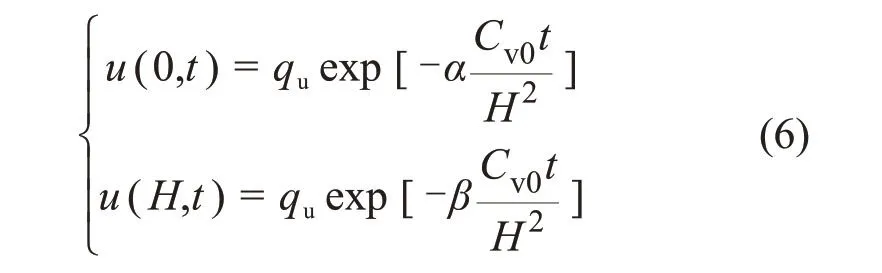
式中：α和β为反映土体顶面和底面排水性状的界面参数；该值可以通过试验模拟或者实测边界处孔压随时间的变化曲线反分析得到。

2 连续排水条件下饱和软土大变形固结的量纲一的解答

将量纲一参数代入式(4)中可得固结方程的表达式为

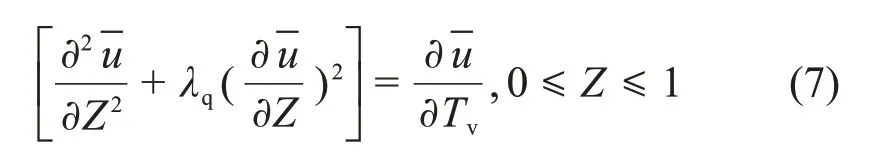
初始条件为

边界条件为

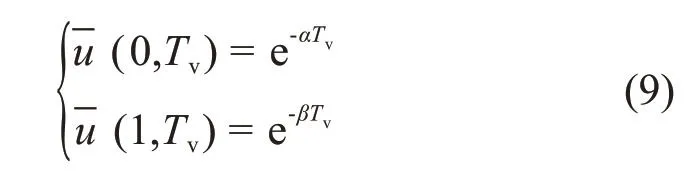
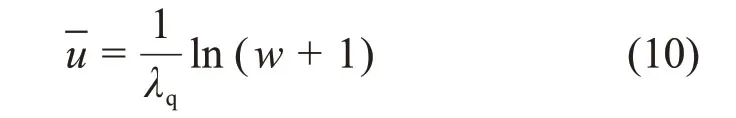
代入式(7)，则固结方程和求解条件可以改写为

初始条件为

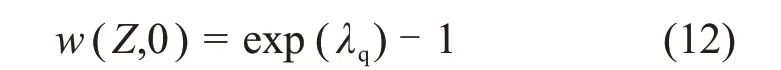
边界条件为

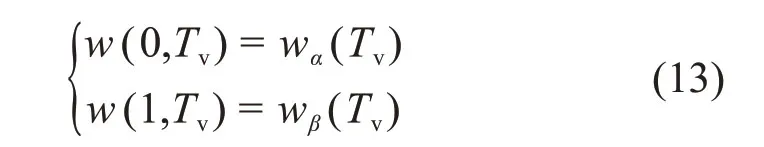
其中：wξ(Tv)=exp(λqe-ξTv)-1。

为了进一步将边界条件齐次化，令

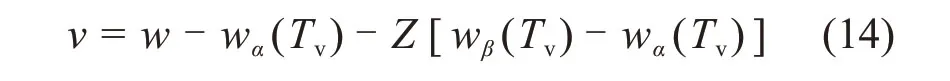
将式(14)代入式(10)可得

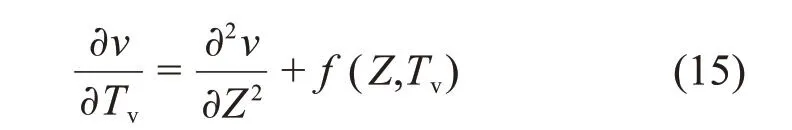
其中：

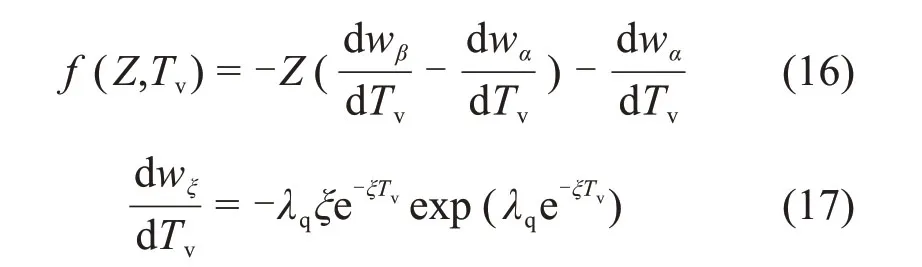
相应的初始条件变为

相应的边界条件变为

对控制方程式(15)和初始条件式(18)采用有限正弦傅里叶变换，再根据边界条件式(19)，有

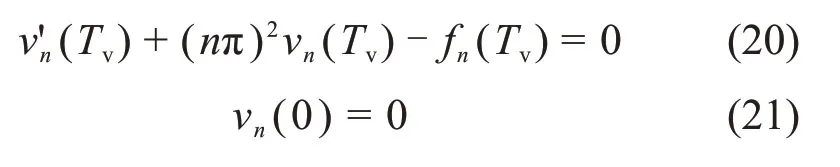
式中：

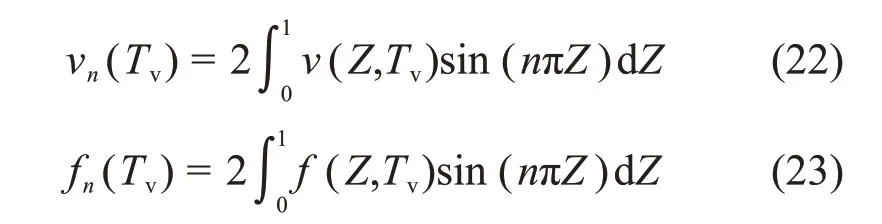
其中：n=1,2,3,…。

根据正弦傅里叶级数可求得：

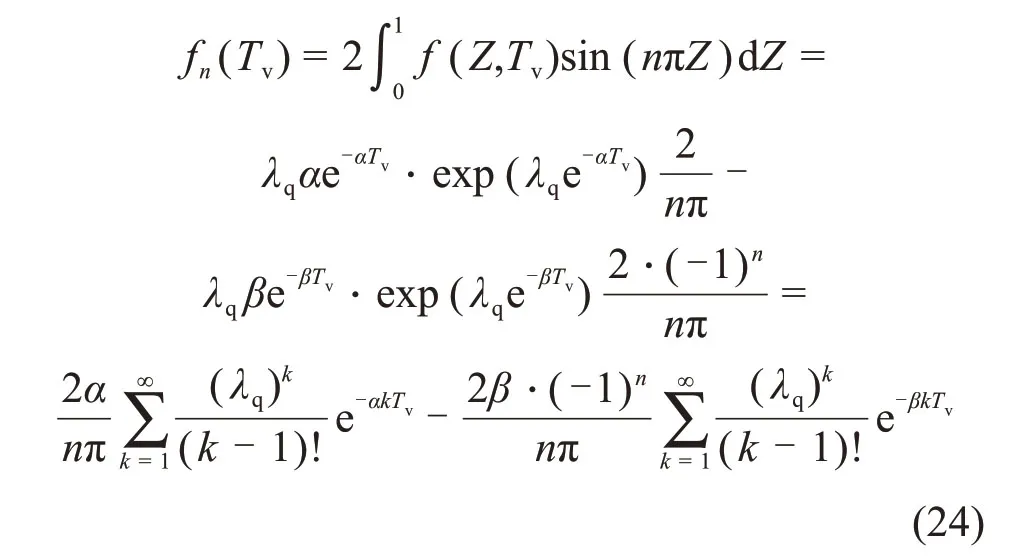
式(24)中对Tv取Laplace变换，则有

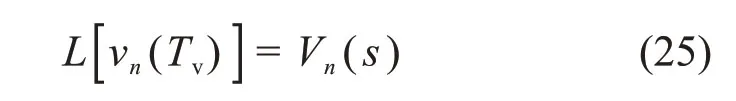
结合初始条件，可得

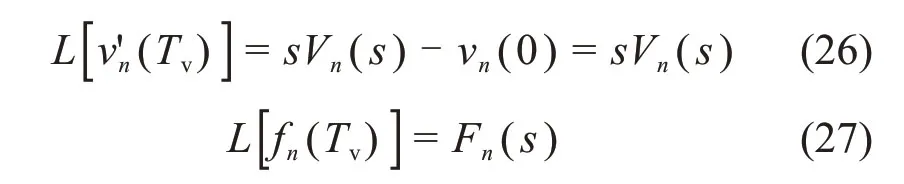
将式(25)～(27)代入式(20)，可得

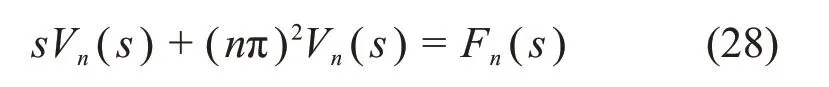
由式(28)可得

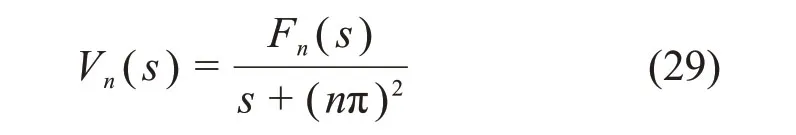
对式(29)求Laplace逆变换，可得

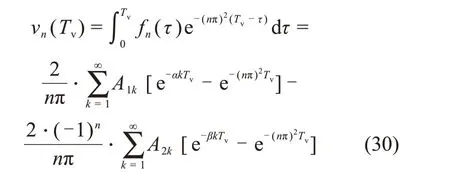
其中：

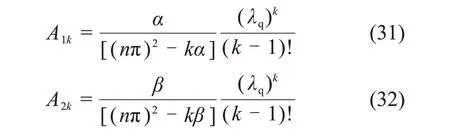
将式(30)代入式(22)，可得

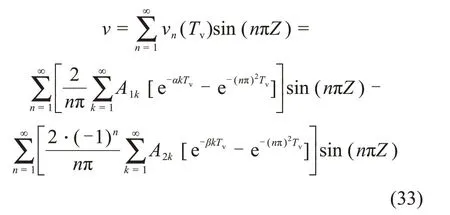
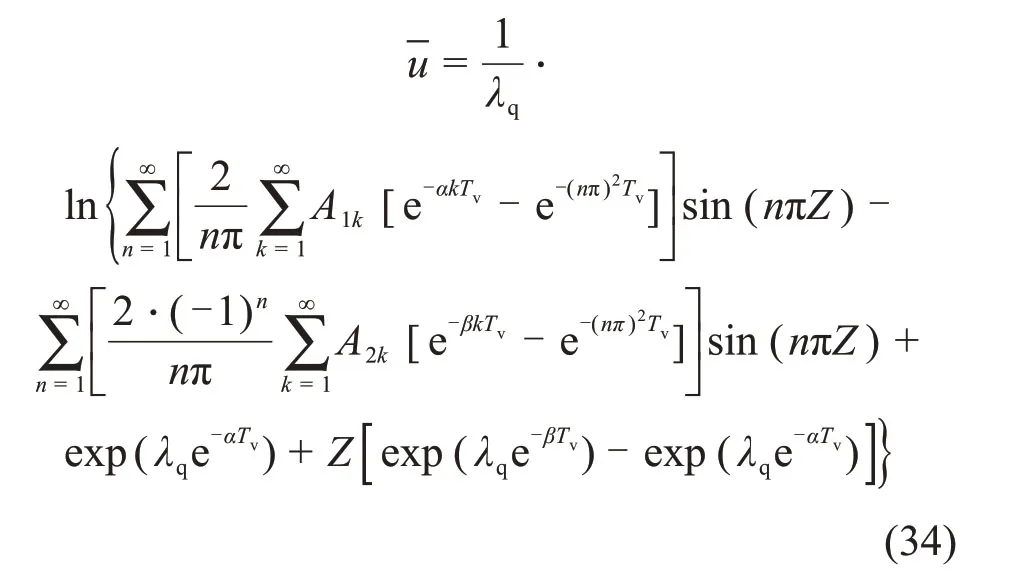
根据饱和软土一维大变形固结理论，土体沉降量的表达式为

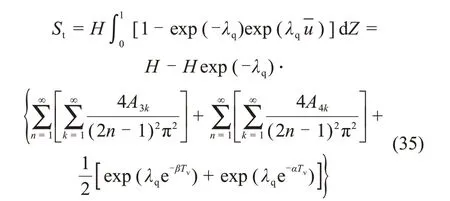
其中：

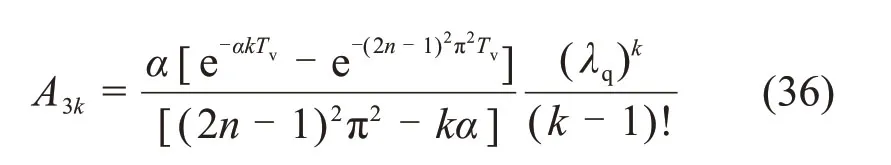
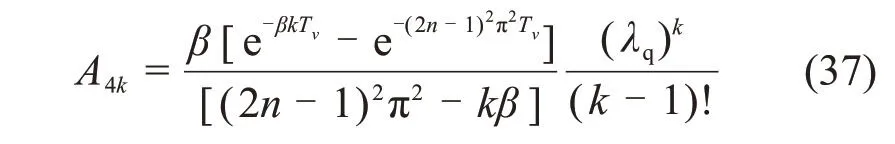
而土体的最终沉降量为

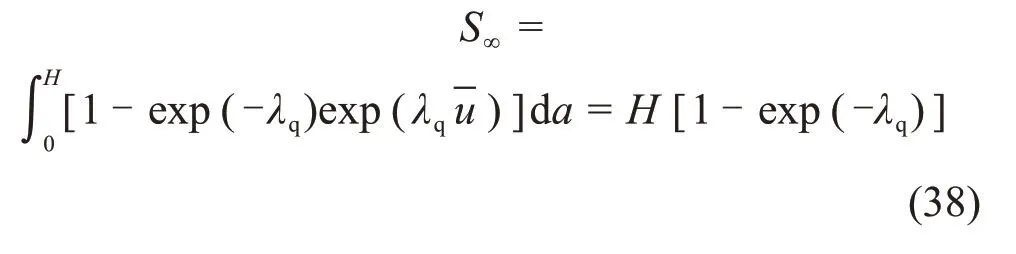
因此，按沉降定义的固结度Us可表达为

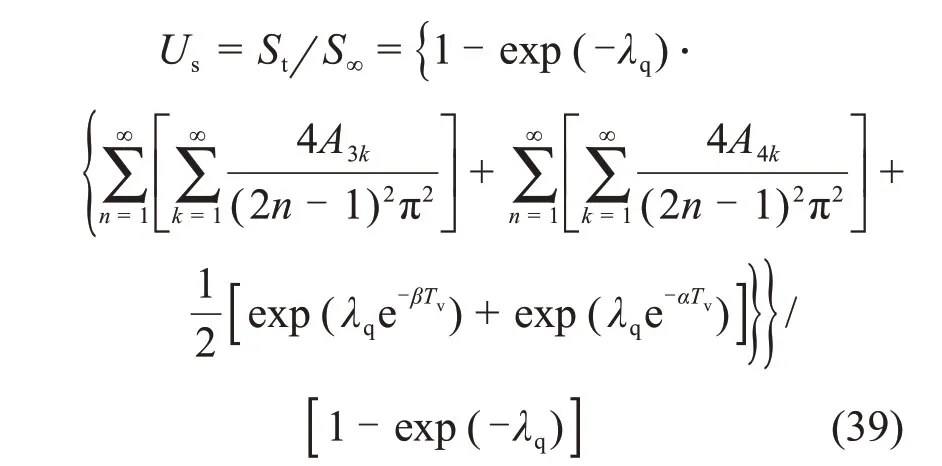
按孔压定义的固结度Up可表达为

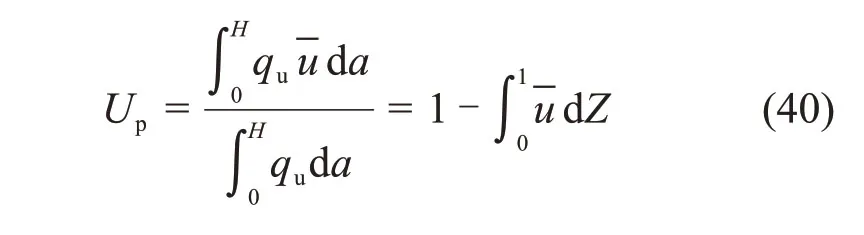
3 解的验证

XIE等[9]求解出饱和软土单面排水条件下一维大变形固结的解答。其求解得到的超孔隙水压力u和按沉降定义的固结度Us的表达式分别为：

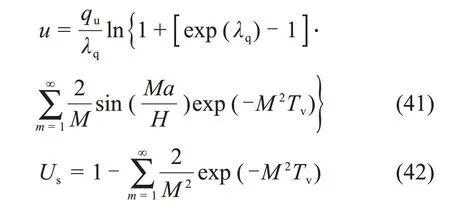
与经典的Terzaghi一维固结理论相比，式(41)中超孔隙水压力u不仅受时间因数Tv的影响，还与无量纲参数λq有关，因此，参数λq是反映土体大变形固结的参数。由定义可知λq=mv1qu，根据上述假定，土体的体积压缩系数mv1在固结过程中保持不变，因此，λq主要受外荷载qu的影响。在这里，可称参数λq为荷载参数。

实际上，只需用H2代替上面的H即可得到对应的XIE等[9]双面排水条件下的一维大变形固结解答，其表达式如下：

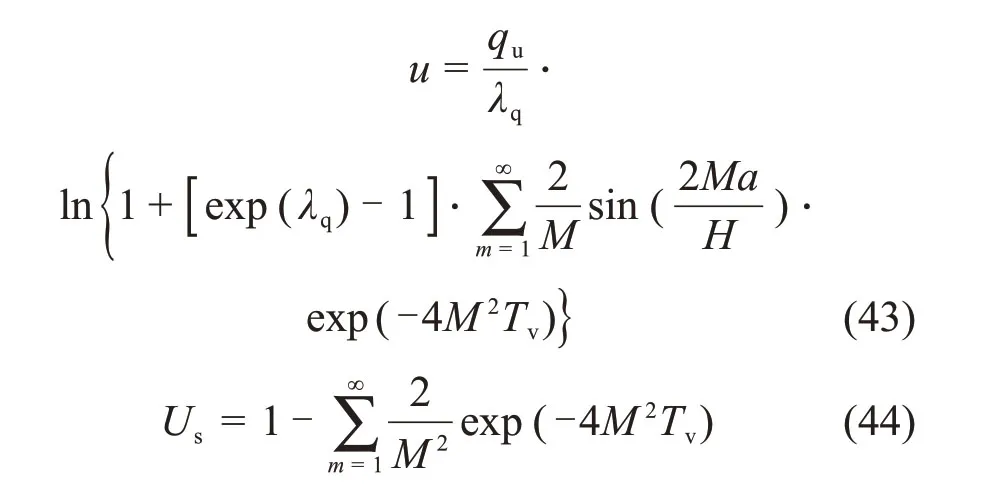
当α→∞和β→∞时，基于连续排水边界所得的解答将退化为XIE等[9]双面排水解答，此时，

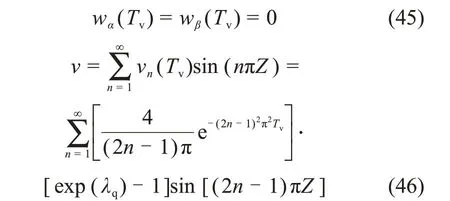
代入式(10)和式(14)可得

因此，

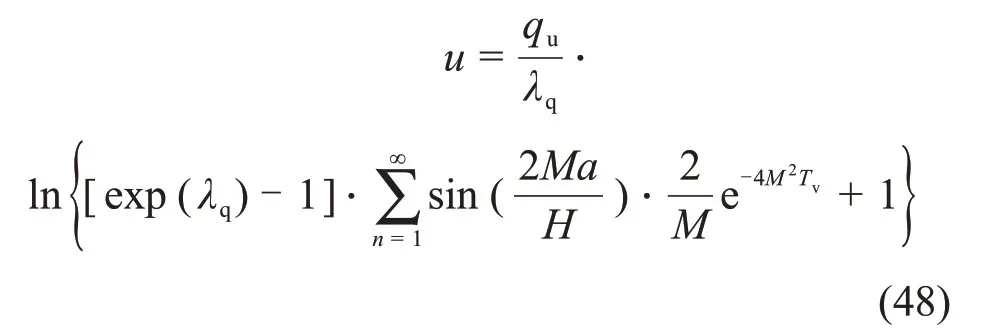
对比可知，退化后的超孔隙水压力u的表达式与XIE等[9]得到的双面排水一维大变形固结下超孔隙水压力u的表达式一致。

同样，将式(48)代入式(39)可求得按沉降定义的平均固结度Us的表达式如下：

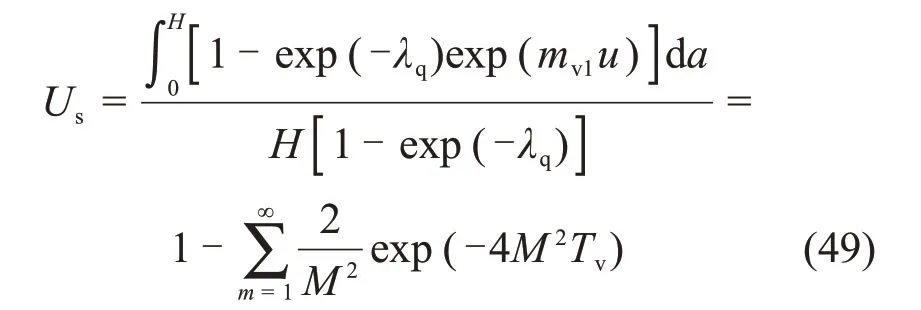
与式(44)对比可知，退化后的沉降固结度与XIE等[9]得到的双面排水条件下按沉降定义的固结度表达式一致。根据退化解析解，可以初步验证连续排水边界条件下饱和软土一维大变形固结解析解的正确性。而根据式(42)和式(44)可知，XIE等[9]得到的单面及双面排水下Us解答只与时间因数Tv有关。而式(39)中，基于连续排水边界求解的Us不仅与Tv有关，而且与荷载参数λq及界面参数α和β有关。

为一步验证上述解答的正确性，对式(7)展开有限差分，利用相应的边界条件和初始条件进行有限差分求解，并将本文解答与有限差分数值解进行对比。假定软土地基在自重及初始荷载q0=10 kPa作用下变形已稳定，取与XIE等[9]研究相同的计算参数(λq=0.4)，其参数如表1所示。为使对比结果具有一般性，取界面参数α=2，β=1。图1所示为2种方法下沉降固结度Us随时间因数Tv的变化。从图1可以看出：本文的解析解与有限差分数值解吻合较好。

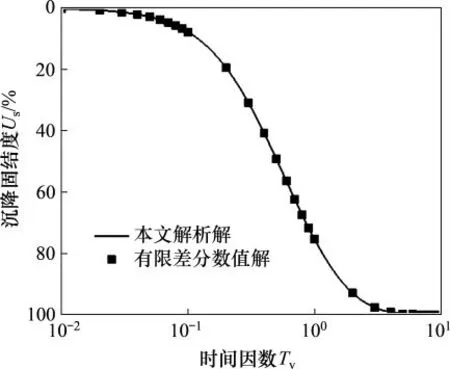
图1 本文解析解与有限差分数值解比较Fig.1 Comparison between analytical solution and finite difference fractional solutions

4 固结性状分析

4.1 α和β取值对固结性状的影响

界面参数α和β对土体的大变形固结过程有着重要影响。以表1中的地基参数为例，图2和图3所示为界面参数对土体孔压的影响曲线。从图2可以看出：界面参数α和β越大，排水边界处的透水性越好，超孔隙水压力消散越快，地基固结速率也越快；当α/β=1时，超孔隙水压力沿相对深度的分布于a/H=0.5处对称。当α/β逐渐增大时，超孔隙水压力峰值逐渐下移，且超孔隙水压力峰值逐渐减小。因此，不同界面参数可模拟土层顶面与底面排水的不同性能。从图3可以看出：当α/β大于1时，上半层土的曲线斜率要明显大于下半层土的曲线斜率，这说明土层顶面的排水速率高于土层底面的排水速率。因此，可以认为界面参数α或β越大，其对应的那半层土的排水速度也就较快。此外，随着时间因数Tv的增大，超孔隙水压力峰值逐渐向较小界面参数值对应面移动。

XIE等[9]研究指出，饱和软土一维大变形固结理论中以孔压定义的固结度Up和以沉降定义的固结度Us存在差异，因此，有必要分别讨论界面参数对孔压固结度和沉降固结度的影响。图4所示为界面参数α和β对孔压固结度Up的影响。图4中曲线4和5分别为XIE等[9]得到的单面排水及双面排水的固结度曲线。对比基于连续排水边界条件得到的孔压固结度与XIE等[9]得到的双面排水孔压固结度可以看出：α和β越大，超孔隙水压力消散越快，其结果也越来接近XIE等[9]得到的双面排水下孔压固结度的解答。从图4还可以得出：当α和β较小时，在固结初期，连续排水边界条件下的孔压固结度明显低于XIE等[9]得到的单面排水条件下的孔压固结度，但在中后期，其结果高于XIE等[9]得到的单面排水条件下的孔压固结度，这主要是由于传统排水边界条件不具连续性。当α和β较大时，尽管在初期连续排水边界条件的孔压固结度与XIE等[9]得到的双面排水下孔压固结度存在较大差异，但2种情况下完全固结所需时间几乎相同。这说明，当排水边界界面参考连续排水边界模型进行设计时，虽然固结初期排水速率较慢，但最终固结时间基本不受影响。

图5所示为界面参数α和β对沉降固结度Us的影响。当沉降固结度Us=90%时，一般可认为沉降已趋于稳定，此时的时间因数定义为Tv90。对于连续排水边界，当β固定为2，α为4，10和100时的Tv90分别为0.909，0.826和0.822，XIE等[9]得到的单面及双面排水条件下的Tv90分别为0.213和0.852。根据Tv90可以看出：当土层一面排水界面参数较小时，增大另一面界面参数对沉降稳定时的固结时间影响不大，且该沉降稳定时间与经典的单面排水下的稳定时间相近。

表1 软土地基的计算参数Table1 Calculation parameters of softsoil foundation

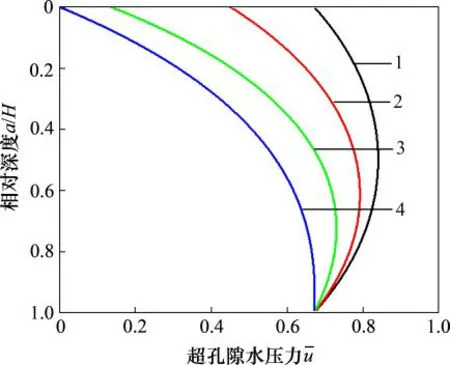
图2 界面参数对超孔隙水压力分布的影响Fig.2 Influence of interface parameterson excesspore water pressure distribution curves

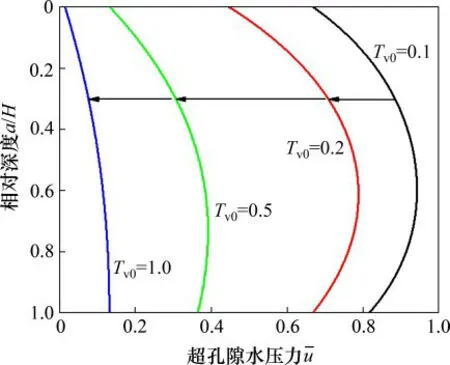
图3 超孔隙水压力随时间因数T v的变化Fig.3 Variation of excess porewater pressure with time factor T v

在实际工程中，当排水边界参考连续排水边界模型进行设计时，可以通过调整α和β设计实际所需的固结排水速率。尽管理论上界面参数的取值是0到正无穷大[19-20]，但从图4和图5可以看出，α和β不用太大，得到的固结曲线就能与XIE等[9]单面及双面排水所得固结曲线相接近。

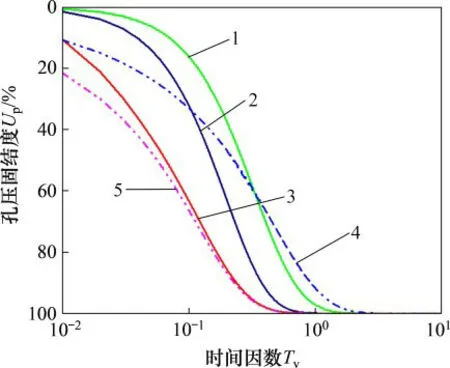
图4 界面参数对孔压固结度Up的影响Fig.4 Influence of interface parameterson Up

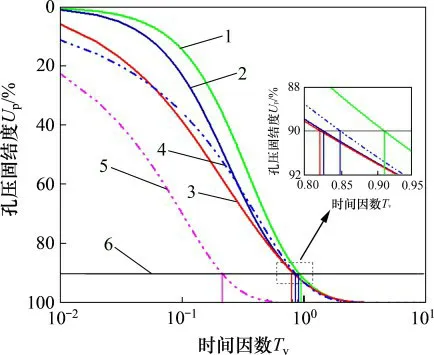
图5 界面参数对孔压固结度Us的影响Fig.5 Influence of interface parameterson Us

4.2 λq取值对固结性状的影响

根据上述分析可知，荷载参数λq主要受外荷载qu的影响。这里以表1中的地基参数为例，外荷载qu分别取25，50，100和200 kPa，以分析不同荷载参数λq对饱和软土大变形固结性状的影响。图6所示为不同λq下的孔压分布。从图6可以看出：λq越大，相同排水边界下超孔隙水压力的消散速率越慢。图6中的孔压分布规律也进一步验证了当αβ=1时，超孔隙水压力沿相对深度的分布于aH=0.5处对称。图7所示为不同λq下连续排水边界退化后的孔压固结度Up曲线。从图7可以看出：在同一时间因数下，孔压固结度随λq的增大而减小。从图6和图7可知：孔压消散速率随λq的增大而减小，这主要是由于外荷载qu越大，土体的渗透系数kv越小，进而降低了土体的孔压固结速率。此外，从图7还可以看出：当α和β取大值(如α=β=1 000)时，基于连续排水边界条件得到的固结曲线和XIE等[9]得到的双面排水条件下的固结曲线一致，即基于连续排水边界条件所得解答可以退化为XIE等[9]得到的双面排水解答，这进一步验证了解答的正确性。

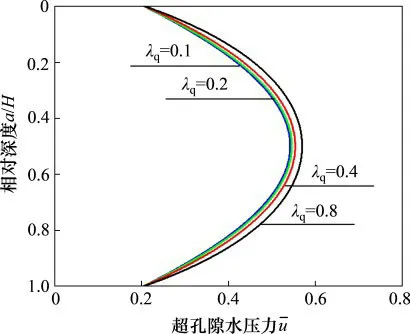
图6 λq对超孔隙水压力分布的影响Fig.6 Influence ofλq on excess pore water pressure distribution curves

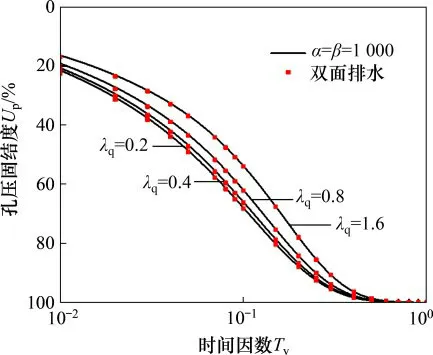
图7 连续排水边界退化后的Up曲线Fig.7 Up curves while continuous drainage boundary degenerated

图8所示为不同边界条件下荷载参数λq对孔压固结度Up的影响。从图8可以看出：在不同排水边界下，孔压固结度均随着λq的增大而减小。对比连续排水边界和XIE等[9]提出的单面或双面排水条件可知，λq对连续排水边界下孔压固结度曲线的影响明显小于XIE等[9]提出的单面及双面排水条件下的影响。在不同的λq下，连续排水边界下的孔压固结度曲线几乎重合，而XIE等[9]得到的单面及双面排水条件下的孔压固结度曲线有明显差异。此外，与图4对比可知，相对于荷载参数λq，界面参数α和β对Up曲线的影响更大。

图8 λq对孔压固结度Up的影响Fig.8 Influence ofλq on Up

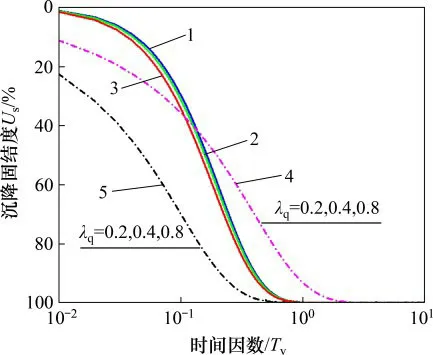
图9 λq对沉降固结度Us的影响Fig.9 Influence ofλq on Us

图9所示为不同边界条件下荷载参数λq对沉降固结度Us曲线的影响。在土体固结过程中，尽管体积压缩系数mv1不变，但由于固结过程中有效应力与孔隙比呈对数关系，土体具有越压越硬的特点，即土体的压缩系数av在固结过程中越来越小。在相同的孔压固结度下，λq越大，压缩系数av越小，沉降固结度Us则越大。从图9可以看出：当时间因数固定时，XIE等[9]得出的单面或双面排水条件下的沉降固结度Us不随λq的变化而变化。这说明尽管固结过程中kv的减小使得土体的沉降固结速率减小，但同时压缩系数av的减小使得沉降固结速率增大，两者的影响相互抵消使得沉降固结度Us不随λq的变化而变化。在连续排水边界下，当时间因数固定时，沉降固结度Us随λq的增大而增大，这与孔压固结度Up随λq的变化趋势刚好相反。这说明连续排水边界下固结过程中kv对沉降固结度Us的影响小于压缩系数av对Us的影响。