阵列式音圈电机定位控制系统的设计

王永龙，刘品宽

(上海交通大学 机械与动力工程学院,上海 200240)

0 引 言

在衡量步进扫描投影式光刻机照明系统的性能时，照明光场积分均匀性是一项关键指标，它直接影响光刻机的特征尺寸均匀性[1]。然而，由于照明系统中镜片装配误差以及镜头本身随着长时间辐照而恶化，照明均匀化单元很难直接达到均匀性要求。因此，高精度光刻机照明系统中必须包含均匀性校正器，用来调整曝光场以达到光刻需求。现阶段45 nm节点以及更高精度的光刻机主要采用手指阵列校正法，图1为手指阵列式校正器示意图，通过调整不透光手指在y方向上伸入照明光场的长度，可以形成强度在x方向上均匀和在y方向上平顶高斯分布的光场。理论上，校正手指宽度越窄、数量越多，通过校正能达到的照明积分均匀性的最小值越小，即校正精度越高[2]。

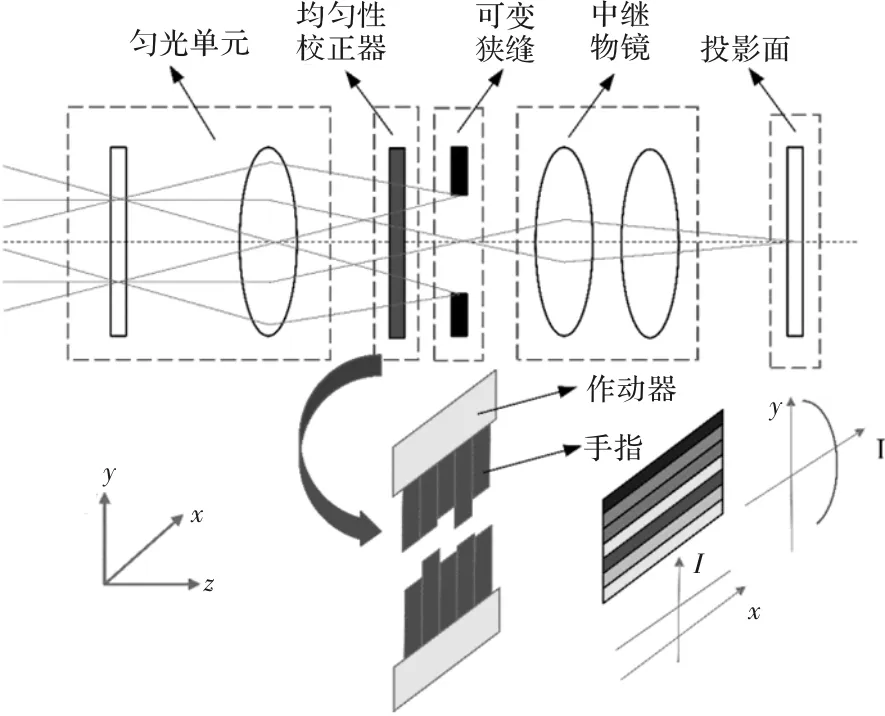
图1 手指阵列式校正器示意图

均匀性校正器通常选择阵列式音圈电机作为作动器，这是因为音圈电机具有响应速度快、频率特性好、体积小、行程输出较大、控制方便和定位精度高的特点。故结合光刻机曝光时间和光场均匀性要求，设计出两套校正器，分别布置在y向上。每套校正器有30轴音圈电机，单轴响应时间在30 ms内，行程为4 mm，定位精度为5 μm。

为了达到音圈电机的超精密运动控制目标，很多学者对运动控制策略进行了大量研究。杨风开等人提出了音圈电机定位的神经网络 PID前馈控制模型，利用BP神经网络在线自整定PID参数，提高了电机定位精度和调节速度[3]。李贤涛等人在PD控制器的基础上，引入了自适应鲁棒控制器，对快速反射镜进行位置控制和扰动抑制[4]。罗定辉等针对音圈电机在运动过程中受负载扰动等非线性因素的影响时，提出了模糊PID参数自整定位置控制策略[5]。

当控制电机轴数过多时，对音圈电机驱动控制提出了很高的要求。而现有的音圈电机控制系统架构主要针对少轴数的控制，且控制方法主要针对扰动状态下的鲁棒性控制，运算较为复杂，不适用于多轴数的超精密定位场景。本文主要针对多轴音圈电机设计出一种以ARM和FPGA作为主控单元的阵列式音圈电机控制系统，采用了CNF和DOB结合的控制策略进行仿真和实验，验证了该控制系统以及控制策略的可行性，对多轴数高精度定位系统有着重要价值。

1 控制系统结构

阵列式音圈电机控制系统是由控制器模块、驱动器模块、位置反馈模块以及阵列式音圈电机运动平台所组成。整体结构如图2所示，其主要包括：基于STM32F407的控制器，基于Spartan6的FPGA读数头信号解码板，基于OPA564的自制线性驱动器，直线光栅，开关电源等。

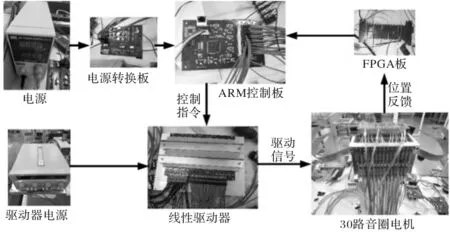
图2 控制系统硬件结构

本系统中的控制板采用主频为168 MHz的ARM处理器和4块8输出的DAC8728，它不仅实现30轴音圈电机的控制算法以及轨迹规划，还负责给线性驱动器输入电压和实时读取编码器的位置。FPGA解码板主要将光栅读数头的差分正交信号转换成位置信息，再通过灵活静态存储控制器(FSMC)与主控板进行并行通讯。自制线性驱动器的响应频率可达到30 kHz，且线性输出效果稳定，零漂小。直线光栅模块由30路MicroE公司的型号为CE300-40的光栅组成，经过FPGA四倍频细分后精度可以达到1 μm。

本设计具有以下特点：①主控板使用多输出的16位DAC，通过STM32自带的外设访问DAC的寄存器，访问速度快且输出电压精度比较高。②解码板使用FPGA进行并行解码和采集30路光栅尺的位置信息，大大缩短闭环周期。③相较于开关型驱动器，自制的线性驱动器带宽高，响应速度快，电流纹波小，输出电压精度高。

2 音圈电机定位的控制模型

2.1 阵列式音圈电机数学模型

阵列式音圈电机是由30路动线圈式音圈电机组成，其整体结构如图3所示。单个音圈电机主要由永磁铁、线圈组成。其中线圈上端与滑条连接，滑条与导轨形成移动副，保证线圈的运动方向平稳；线圈下端与手指连接，用来改变照明光场的均匀性。当通电线圈在磁场中时，会产生推力，驱动线圈在磁场中沿导轨方向直线运动，且随着电流方向和数值变化，线圈做往复直线运动。

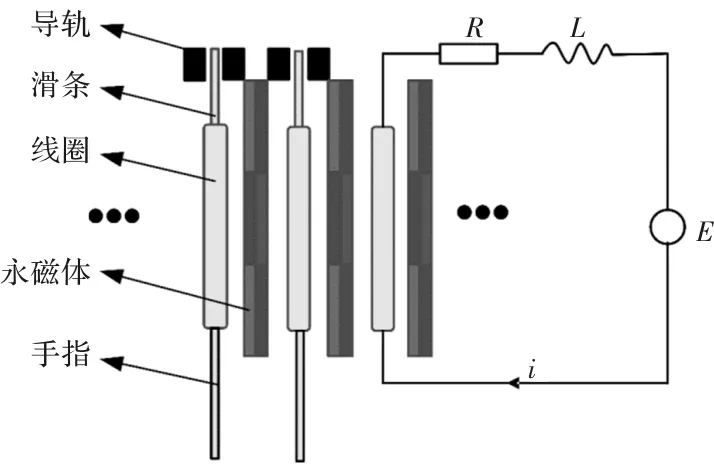
图3 阵列式音圈电机结构示意图

由于该结构中存在导轨与滑条之间的摩擦，且在超精密定位中，须考虑空气阻尼、电涡流阻尼以及弹性刚度对系统的影响，所以音圈电机的数学模型建立采用质量-阻尼-弹簧型模型。根据电压平衡方程和力平衡方程建立音圈电机数学模型：

(1)

式中，E，i，x，F为电源电压、电路中电流、位移和电磁力，L和R为音圈电机中等效电阻和电感，m，c，k，Km，Ke分别为系统质量、阻尼系数、弹性系数、电机力常数和反电动势常数，其中Km=Ke=Bl。从式(1)中消除中间变量F和I，可得到输入电压和输出位移的音圈电机微分方程:

(2)

将式(2)进行拉普拉斯变换，可得到线圈位移和电压之间的传递函数为

(3)

2.2 阵列式音圈电机控制指令规划

为了减小音圈电机在运动过程中引起的冲击，输入指令需要进行轨迹规划[6]。考虑到控制精度和响应时间，本文运动轨迹规划采用5阶S型曲线。结合实际需求，规划的性能指标优化函数为最小时间和冲击的线性组合，且设定音圈电机运动轨迹为在0 mm处和4 mm处进行往复直线运动，具体运动状态如下表所示。

表1 电机运动状态表

规划后得到位置曲线、速度曲线、加速度曲线分别如图4、图5、图6所示，可以看出在整个运动过程中的速度和加速度在任何时间点都没有存在突变的情况，且运行速度快，冲击相对比较小。

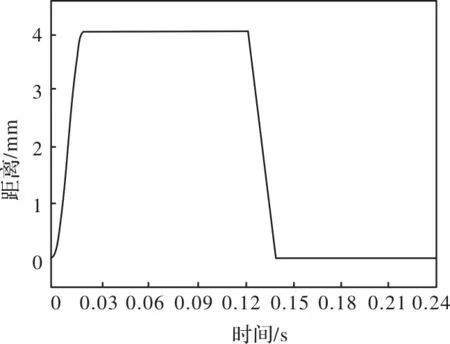
图4 规划后的位置曲线

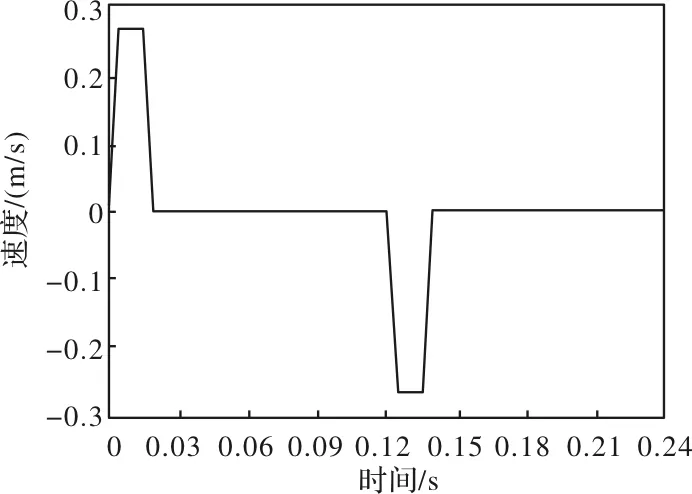
图5 规划后的速度曲线

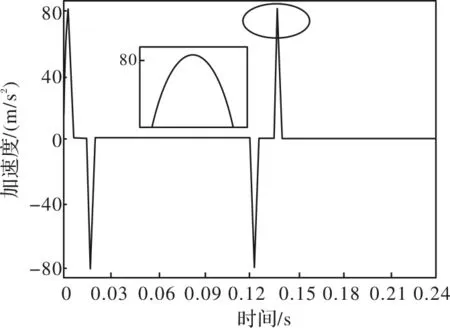
图6 规划后的加速度曲线

3 控制器设计

传统复合非线性反馈控制主要包括线性反馈控制和非线性反馈控制，线性反馈控制部分主要调整系统的平衡点和产生较小的阻尼，提高响应时间，随着系统输出接近平衡点时，非线性反馈控制部分则增大闭环系统的阻尼比，减小超调量[7-8]。但是，传统CNF控制没有考虑到扰动因素的影响，当系统中存在扰动时，CNF的控制策略通常无法达到精确的控制效果。为消除扰动的影响，通常可以考虑两种方法：①对扰动进行估计和补偿。②引入积分控制。积分控制是常用的方法，但参数调试时容易造成积分饱。所以本系统采用DOB结合CNF的控制策略，以达到快速响应、低超调和鲁棒性强的控制目标。

3.1 CNF控制器设计

典型的音圈电机伺服系统是一个控制输入饱和的单输入单输出系统，如式(4)所示。

(4)

首先，设计线性反馈控制器，主要目标是调整原有系统的阻尼和平衡点。

uL=Fx+Gr

(5)

式中,r为要达到的系统输出，F和G为要设计的定常矩阵。将式(5)代入式(4)可得，

(6)

此时可以选取合适的F矩阵，保证A+BF为Hurwitz稳定矩阵，即可达到系统渐近稳定的目标。下面设计矩阵G，确保系统输出跟随系统的参考输入，即满足式子

(7)

构建变量Δx=x-xd，其中C1xd=r，代入式(6)可得：

(8)

令(A+BF)xd+BGr=0可得，

G=-[C1(A+BF)-1B]-1

(9)

xd=-(A+BF)-1BGr

(10)

其次，设计非线性反馈控制器uN，一般非线性反馈率为

uN=ρ(r,y)BTP(x-xd)=ρ(r,y)BTPΔx

(11)

其中,ρ(r,y)非正且符合Lipschitz条件，这里可取

(12)

在输出向指令趋近的过程中，可看出ρ(r,y)从0向-β变化，即在初始时刻，非线性部分输出很小，在输出接近设定值时，非线性反馈输出比较大，从而改变闭环系统阻尼比来抑制超调量的产生。

下面来证明复合非线性反馈控制器的稳定性。综合式(5)和式(11)，可得最终控制器为

u=uL+uN=Fx+Gr+ρ(r,y)BTPΔx

(13)

由式(5)、式(9)、式(10)可得

uL=FΔx+(1-F(A+BF)-1B)Gr=FΔx+Hr

(14)

其中,H= (1 -F((A+BF)-1B)G，且容易验证，

Axd+BHr=0

(15)

则由式(4)、式(13)、式(14)、式(15)可得，原系统可转换为

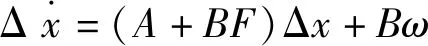
(16)

其中,

ω=sat(uL+uN)-(Hr+FΔx)

(17)

由于A+BF为Hurwitz稳定矩阵，则对任意给定的正定实对称矩阵W，必存在正定的实对称矩阵P，满足

(A+BF)TP+P(A+BF)=-W

(18)

定义李雅普诺夫函数V(Δx)=ΔxTPΔx，则

(19)

根据饱和限幅函数的取值，ω的取值不同，三种情况分析分别如下：

(1)当|uL+uN|≤umax时，由式(11)、式(14)和式(17)可知ω=uN=ρBTPΔx，此时

(2)当uL+uN>umax时，则有0<ω=umax-uL0可得BTPΔx<0此时

(3)当uL+uN<-umax时，则有uN<ω=-umax-uL<0，同(2)得BTPΔx>0

综上可知，复合线性反馈控制器是稳定的，且可以收敛到指定位置。

3.2 干扰观测器设计

干扰观测器的基本思想是将外力干扰及模型参数变化造成的实际对象与名义模型输出的差异等效为控制端的输入，即观测器的干扰输出，然后在控制中引入等量的补偿，实现对干扰完全抑制[9]。由于系统的精确数学模型无法得到，并且测量的高频噪声无法消除，所以需要在扰动观测器输出加入一个低频滤波器。本系统的干扰观测器的结构如图7所示。

图7 DOB系统结构图

根据梅森公式可得传递函数表达式

(20)

(21)

(22)

(23)

其中,M=0, 1, …,N-1。N-M为滤波器的相对阶数，为滤波器的时间常数。理论上，Q(s)的带宽越宽，阶数越高，干扰观测器的响应速度就越快，干扰的抑制效果就越好。但随着阶数的增加，大的相位滞后会产生欠阻尼状态，使系统不稳定。所以，该滤波器的设计要综合考虑观测器的鲁棒稳定性和干扰抑制能力。

4 仿真与实验结果分析

4.1 算法仿真

为了验证上述控制算法的可行性，首先在Simulink中搭建控制框图进行仿真。音圈电机的具体参数为：线圈电感L为2.63 mH，电阻R为26.5 ，动子质量为0.1 kg， 电机力常数Km为10.2 N/A，电机阻尼系数c为5.49 Ns/m，定位运动方向刚度k记为0。由于电机电感比较小，为了便于设计控制器，可将其忽略。最后得到音圈电机模型为

写成状态空间表达式可得

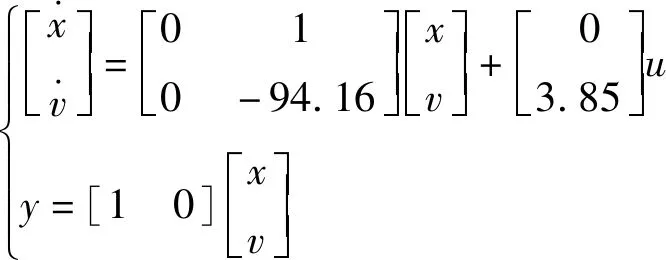
式中,x为音圈电机动子位置，v为电机速度。

首先设计线性反馈控制器，根据极点配置和式(9)可得

其中,k1=-ω2/b，k2=-2ξω/b，b=3.85。ξ和ω为可调节常数，决定闭环系统的极点初始位置。

然后设计非线性控制器，取对称正定矩阵

则由式(18)可算出

本设计中取ξ=0.35，ω=200，μ=0.1。

最后设计DOB，取N=3，M=1，=0.001，由式(23)可得滤波器为

输入位置指令为5阶S型曲线，无外界扰动和测量噪声的CNF控制算法仿真结果如图8所示，有外界扰动和测量噪声的CNF控制算法仿真结果如图9所示，有外界扰动和测量噪声的CNF与DOB相结合的控制算法仿真结果图如10所示，控制算法的性能参数如表2所示。

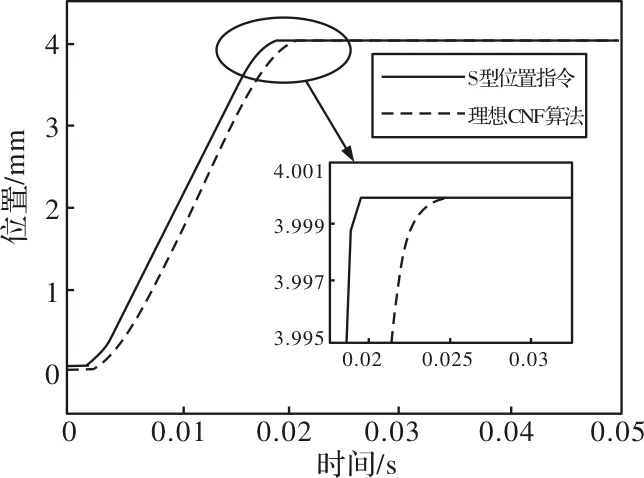
图8 理想CNF算法仿真曲线图

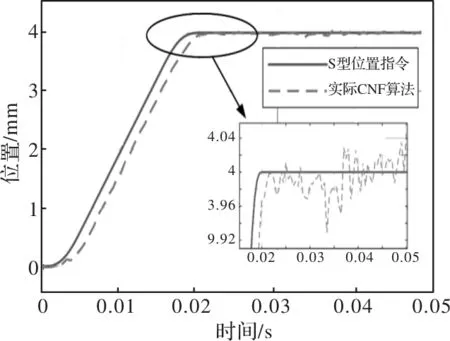
图9 实际带有扰动的CNF算法仿真

图10 带有干扰观测器的CNF算法仿真图

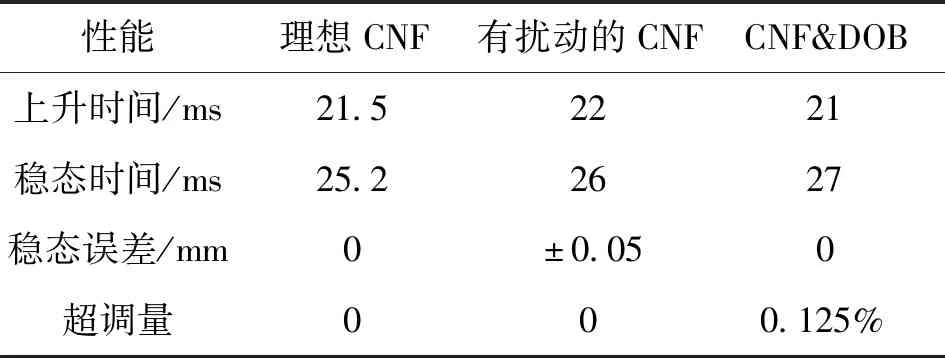
表2 控制算法仿真实验对比

从仿真结果看出，理想情况下的CNF控制算法响应速度快，没有超调和稳态误差；当在输入端加入低频扰动和测量端加入高频噪声时，可以看出CNF算法不能满足定位要求，稳态误差达到了50μm；最后使用DOB和CNF结合的控制策略，可以看出仿真结果比较理想，表明该算法能够抑制外界扰动且定位精度高，响应速度快、超调量小。

4.2 系统实验

在本实验装置中，控制器设计和指令轨迹规划在ARM中进行，输出为数字量。然后输出的数字量经过DA转换为模拟量，输入到线性驱动器进行放大。最后电机接收到驱动器的电压进行定位运动，位置信息通过FPGA反馈给控制器中，形成伺服闭环。

在系统实验中，该控制系统能同时驱动30轴独立运动，图11为其中一轴的系统实验跟踪曲线，从图中可以看出该系统定位精度高、响应速度快且低超调。这表明该控制系统设计合理，且控制算法设计满足光刻机均匀性校正器的运动指标要求。

图11 系统实验轨迹跟踪图

5 结 论

本文首先介绍了光刻机均匀性校正器的作用原理，提出了基于阵列式音圈电机的控制系统设计，并详细介绍了控制系统的硬件架构。然后结合系统数学模型设计CNF与DOB相结合的控制算法，并对输入轨迹进行合理的规划。最终仿真和实验表明：该控制算法和硬件系统能够有效地抑制了外界的扰动，在电机控制的鲁棒性、快速响应性、低超调以及定位精度等方面有着优越的性能。