低共模干扰的永磁同步电机驱动系统模型预测控制

申 科，郎 朗，刘卫国，赵 丹

(西北工业大学 自动化学院，西安 710129)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Generator, PMSM)具有体积小、重量轻、效率高、性能稳定等优点，是新一代航空、航天、航海用电机的重要发展方向，广泛应用于要求高控制精度和高可靠性的场合[1]。随着飞机电作动系统中电气集成的发展和大规模电子设备的使用，系统的电磁干扰(Electromagnetic Interference, EMI)问题变得更加复杂。三相电压源逆变器(Voltage Source Inverter, VSI)被广泛用于永磁同步电机驱动系统，随着半导体器件的不断应用，电机驱动系统产生的共模(Common Mode, CM)干扰对系统的可靠性产生严重的威胁，如绝缘失效、轴电压等问题。

目前，降低共模干扰的方法大致可分为两类：降低干扰源的发射强度和切断传导路径。阻断EMI传播路径通常采用EMI滤波器结构，包括无源滤波器[2]，有源滤波器[3]，以及混合滤波结构[4]。此外，通过改进调制策略以降低共模电压(Common Mode Voltage, CMV)发射强度的方法为系统优化设计提供了新思路。文献[5]比较了SVPWM (Space Vector PWM)、DPWM (Discontinuous PWM)及AZSPWM (Active Zero State PWM)在两级三相VSI系统的CMV性能。

模型预测控制(Model Predictive Control, MPC)由于其实现简单、控制灵活、可同时控制多目标等突出优点而广泛应用于大量功率变换器和电气驱动领域[6]。这些优点使得MPC用于CMV抑制成为了可能。目前，MPC在电机驱动系统的研究主要集中在电机控制方面[7]。为了补偿系统因延时造成的控制误差等，文献[8]介绍了带有延时补偿的MPC，文献[9]采用了多步预测的方式实施延时补偿。采用MPC控制技术降低逆变器共模电压的研究在电机驱动系统中也得到了发展。在传统的MPC基础上，文献[10]和文献[11]避免了零矢量的使用以消除共模干扰，并考虑了死区时间的影响；为了进一步减小负载电流纹波，文献[12]在不使用零电压矢量的基础上，研究了每个采样周期选用两个非零矢量的CMV抑制策略。

本文对永磁同步电机驱动系统中的共模干扰问题进行研究，提出了具有共模电压抑制能力的新型改进MPC方法，在系统延时和开关频率两方面做了相应的优化措施。最后通过仿真验证了该方法的有效性。

1 基于传统MPC的PMSM驱动系统

1.1 PMSM驱动系统数学模型

PMSM电驱动系统由直流电压源、三相逆变器及PMSM组成，其中，三相逆变器采用传统的两电平结构，如图1所示。

三相逆变器的工作状态可由上桥臂的开关管的工作状态Sk(Sa,Sb,Sc)表示，Si=1表示开通状态，Si=0表示关断状态。

因此三相逆变器可产生8种不同的工作状态，对应8个电压矢量，分别为V0(000),V1(100),V2(110),V3(010),V4(011),V5(001),V6(101),V7(111)，其中包括6个非零电压矢量及2个零电压矢量，如图2所示。

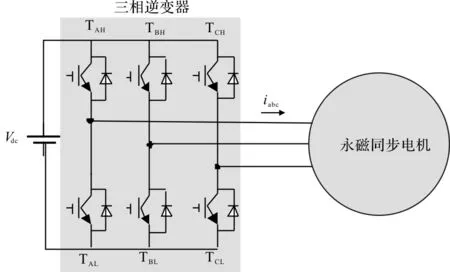
图1 PMSM系统示意图

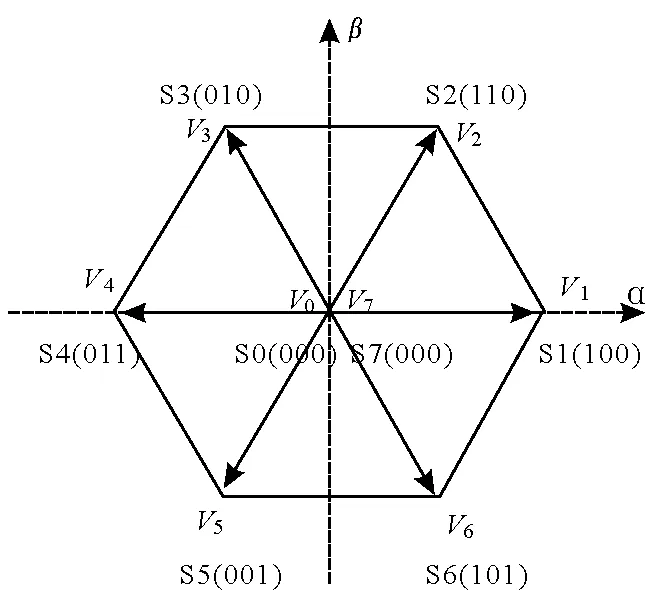
图2 三相逆变器电压矢量示意图

传统的MPC方法尝试建立模型并预测下一时刻的变量，根据一个或多个被控目标构建代价函数，以代价函数最优来决定下一时刻作用的最佳电压矢量。在PMSM驱动系统中，MPC方法一般使用8个电压矢量。PMSM驱动系统在d-q坐标系下的电压方程可表示为

(1)

式中，Vd、Vq为定子电压，id、iq为定子电流，Ld、Lq分别为d、q轴电感，Rs为定子电阻，ωr为转子转速，ψf为永磁通量。则在tk-1，定子电流is可表示为

(2)

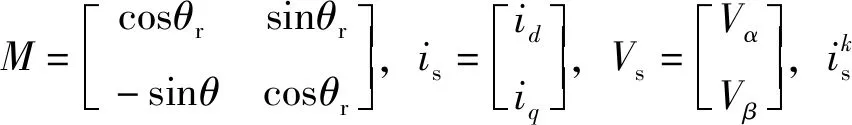
1.2 带延时补偿的MPC

本文采用模型预测电流控制(Model Predictive Current Control, MPCC)，则可构建以定子电流为控制目标的如下代价函数：

(3)

图3 传统MPC框图

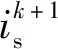
(4)

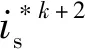
(5)

则包含延时补偿的MPC代价函数为

(6)

2 考虑共模干扰抑制的MPC方法

2.1 PMSM驱动系统中共模电压的定义

共模电压定义为负载中性点和地之间的电压，可表示为

(7)

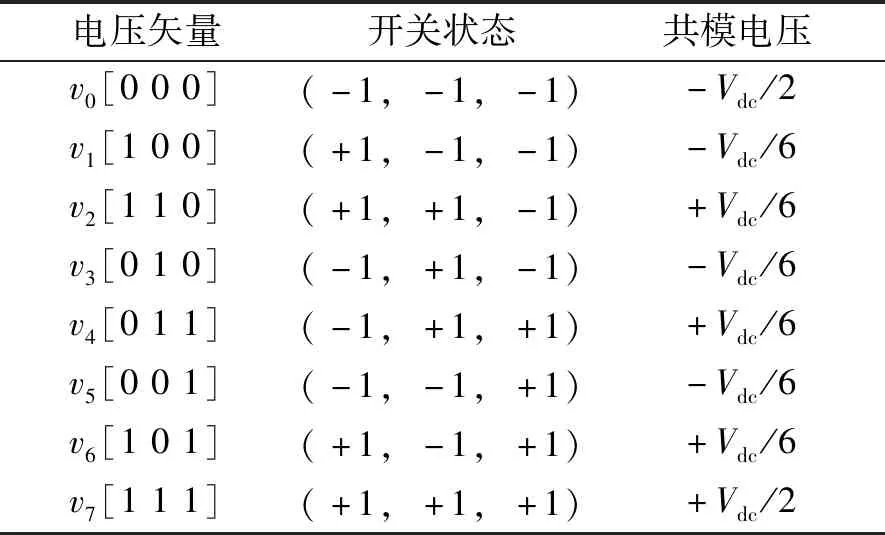
表1 不同电压矢量对应的共模电压

其中，uio=(Si-1/2)udc是第i相电压，udc是直流电压，Si是第i相开关状态。表1是八个电压矢量对应的共模电压，从表中可以看出，对于零电压矢量V0和V7，共模电压峰值均为直流电压的一半，而对于六个非零电压，共模电压峰值只有直流电压的六分之一。因此，避免零电压矢量的使用可以有效降低共模电压峰值。

2.2 考虑开关频率的MPC算法优化

在每个采样时刻，传统MPC方法需要对每个电压矢量均进行代价函数计算与比较，这大大的增加系统的运算负担，降低了系统的运行效率。此外，传统MPC允许任意开关状态之间的切换，这将导致系统的开关频率提高，系统效率的降低，在极端情况下可能出现三相桥臂同时换向的情况。针对上述问题，本文进行了电压矢量的优化选择：相比于传统MPC允许任意开关矢量之间的切换，本方法只允许不相对的电压矢量间的切换，即相邻的两个电压矢量和原矢量间的切换，如图4所示。例如，若在tk时电压矢量对应的开关状态为“010”，则tk+1时刻的电压矢量需从开关状态为“010”，“110”，“100”，“001”和“011”五个电压矢量中进行选择，而不能选择和“010”相对的“101”电压矢量。

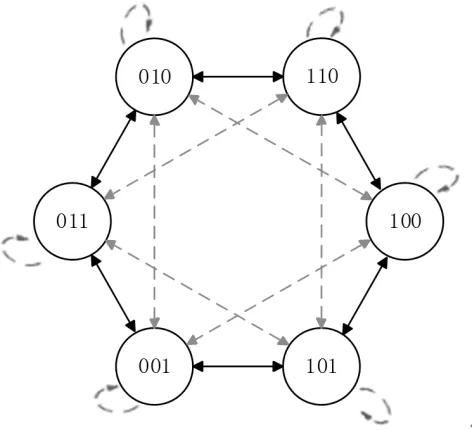
图4 优化的矢量选择方法

开关频率可以由下式表示：

(8)

其中,Sa(k+1)，Sb(k+1)和Sc(k+1)是tk+1时刻三相桥臂对应的开关状态。为了优化系统的开关状态选择，将开关频率作为被控目标加入到代价函数中：

(9)

式中，λ为控制开关频率的权重系数。

2.3 考虑共模电压抑制的MPC方法

图5为所提出的共模干扰抑制MPC方法的控制策略流程图，其实现步骤如下：

(1)在tk时刻实施由前一时刻选择的开关矢量Sk；

(2)从电机系统获得定子电压Vd、Vq，定子电流id、iq，电机转速ωr，转子位置θr；

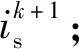
(5)根据式(9)计算代价函数g，并选择使其最小的电压矢量；

(6)输出对应的开关状态Sk+1，并储存此次循环中选择的电压矢量所预测得到的定子电流，用在下一循环的延时补偿中。

图5 控制方法流程图

3 仿真结果与分析

为了验证本文所提出方法的有效性，在Matlab/Simulink中搭建PMSM驱动系统仿真系统，仿真参数如表2所示。

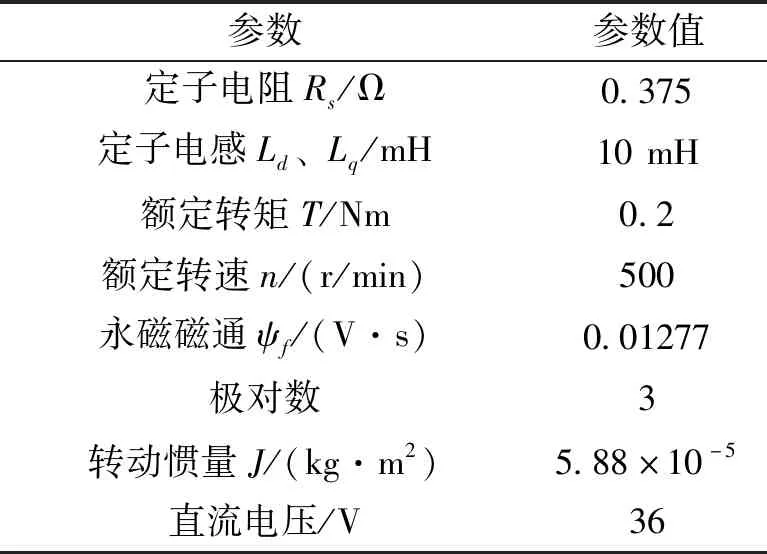
表2 仿真参数表

对传统的MPC控制，带延时补偿的MPC控制，以及本文所提出的带延时补偿及共模电压抑制的改进型MPC控制三种方法进行了仿真比较。

图6与图7分别为传统MPC控制以及带延时补偿的MPC控制的电流仿真波形，可以看出，延时补偿可以减小定子电流纹波。

图6 传统MPC电流波形图

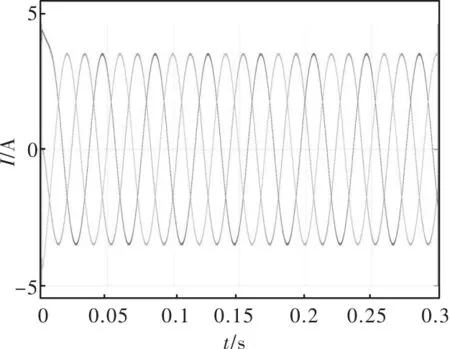
图7 有延时补偿MPC电流波形图

图8和图9分别为带延时补偿的MPC和改进型MPC两种方法的共模电压在时域仿真波形。可以看出，本文所提出的方法将共模电压峰值降低至原先的三分之一(从18V到6V)。图10为带延时补偿的MPC和改进型MPC两种方法的频域仿真效果对比。可以看出，本文所提的改进型MPC方法的共模电压抑制效果在频域内十分明显。在传导干扰测试频段100k～30M内，共模干扰平均值可降低8 dBm。

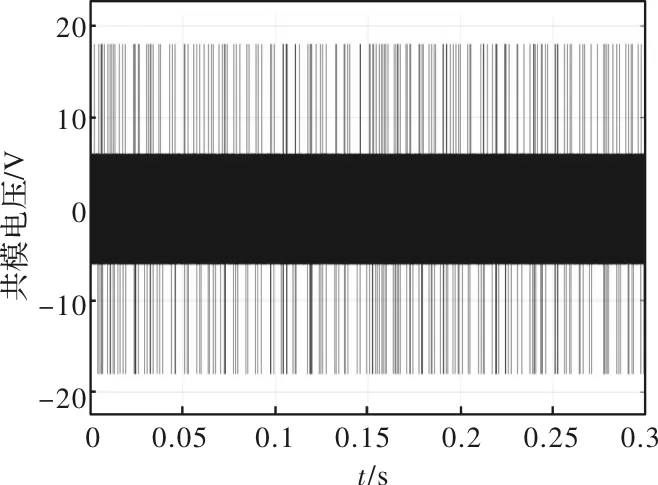
图8 传统MPC共模电压波形图

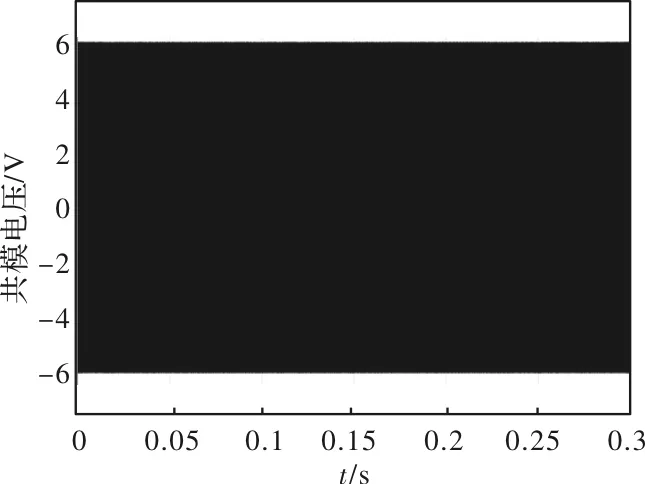
图9 改进型MPC共模电压波形图

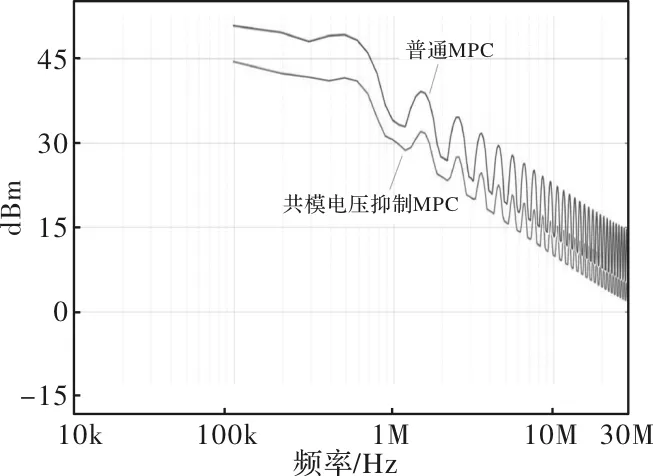
图10 传统MPC与改进型MPC共模电压对比图(频域)

4 结 论

基于传统的永磁电机驱动MPC控制系统，本文提出一种综合考虑系统延时、开关损耗、共模电压抑制的改进型MPC控制技术。仿真结果表明采用延时补偿方法可以有效的提高定子电流质量；同时，传统的MPC控制，带延时补偿的传统MPC控制及本文所提出的带延时补偿及共模干扰抑制的改进型MPC控制技术的时域、频域仿真对比结果表明：所提的新型改进MPC方法可以有效地降低CMV的时域及频域发射强度。