机器人关节无框电机转矩脉动抑制
2020-06-17黄玉平郭喜彬佟文明陶云飞原誉桐
陈 靓,黄玉平,郭喜彬,佟文明 ,陶云飞,原誉桐
(1.北京精密机电控制设备研究所,北京 100076;2.沈阳工业大学,沈阳 110870)
0 引 言
近年来,无框电机在医疗机器人、无人机推进和制导系统等领域中的应用越来越广泛,这与其体积小、功率高、低惯量与结构紧凑等特性密不可分[1-2]。然而,在某些对速度波动较为敏感的场合,电机较大的转矩脉动会导致无法挽回的损失。故电机是否具有超低的转矩脉动以及高精度的齿槽定位,是一个需要研究的问题。
目前无框电机的代表性产品有美国科尔摩根的TBM无框力矩电机、Parker公司的K系列无框伺服电机、Aerotech公司S-series高性能无框力矩电机以及Alliedmotion公司的无框力矩电机等[2]。
在文献[3-6]中,提出了通过对永磁体进行Halbach充磁的方式,使气隙磁场具有理想的正弦分布,以大大降低电机的齿槽转矩与转矩脉动。但由于该充磁方式较为复杂,安装工艺较为繁琐,故在无框电机中应用较为受限。
为了最大化降低无框电机的转矩脉动,本文分析总结了电机不同结构对转矩脉动的影响,并通过优化极槽配合、转子磁极结构等手段降低其转矩脉动,改善运行平稳性。基于这些分析,将有限元仿真结果与一台118W、4300r/min机器人关节无框永磁同步电动机试验结果进行了比较,验证了该优化方案的有效性。
1 转矩脉动成因及削弱方式
永磁同步电机在运行过程中,由于谐波磁动势和齿槽效应的影响,会产生较强的转矩脉动。永磁电机的电磁转矩为
Tem=Tavg+Tcog+Tv
(1)
式中,Tem为电磁转矩;Tavg为平均电磁转矩;Tcog为齿槽转矩;Tv为谐波转矩。其中齿槽转矩计算公式为
(2)
式中,α为转子位置角;L为铁心轴向长度;R1与R2分别为定子外半径与定子轭部半径;B为永磁体沿圆周方向的剩磁密度;Gn为傅里叶分解系数。
由式(1)可知,通过降低电机齿槽转矩与谐波转矩,即可降低电机的转矩脉动。目前国内关于无框电机转矩脉动抑制技术研究并不多,本文分析总结了无框电机不同结构对转矩脉动的影响,并通过优化极槽配合、转子磁极结构等手段降低其转矩脉动,改善运行平稳性。
2 电机结构及主要参数
图1为一台12极39槽机器人关节无框电机示意图,其主要参数如表1所示。本文在该模型的基础上,通过有限元仿真,研究电机不同结构对转矩脉动的影响。

图1 电机仿真模型
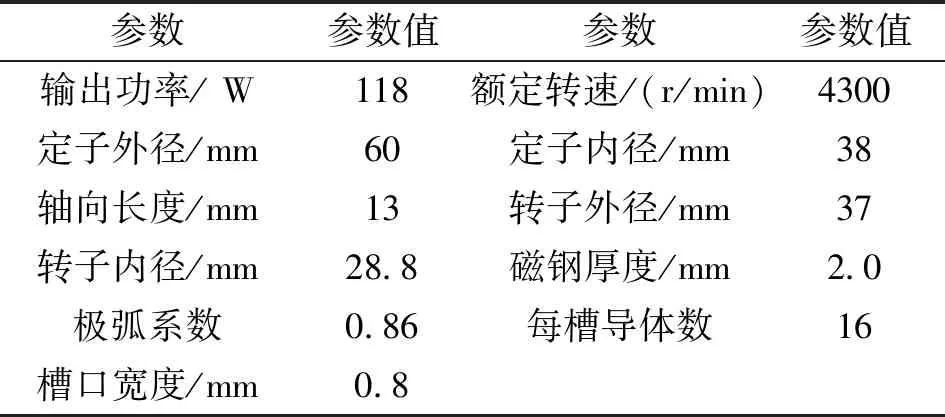
表1 机器人关节无框电机主要参数
3 电机不同结构对转矩脉动影响
在负载转矩仿真计算过程中,电机的电流均按照正弦电流波形进行计算,且除表面插入式转子磁极结构外,均采用Id=0进行仿真,且仿真电流值为4.65A[7]。
3.1 不同极槽配合分析
由于无框电机的产品标杆科尔摩根电机大多采取用12极39槽配合,故首先分析此极槽配合下的无框电机性能。该极槽配合具有不同的绕组分相方式,分别如图2(a)、图2(b)所示。

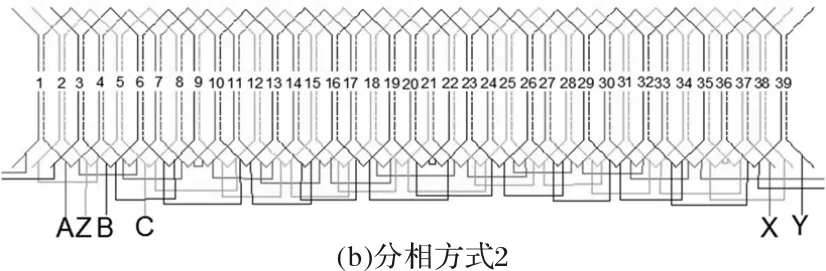
图2 12极39槽两种不同的绕组分相方式
从表2所示的空载反电动势计算结果来看,电机采用分相方式2时的空载反电动势有效值更大,且转矩脉动更小,故优先选用该种分相方式。
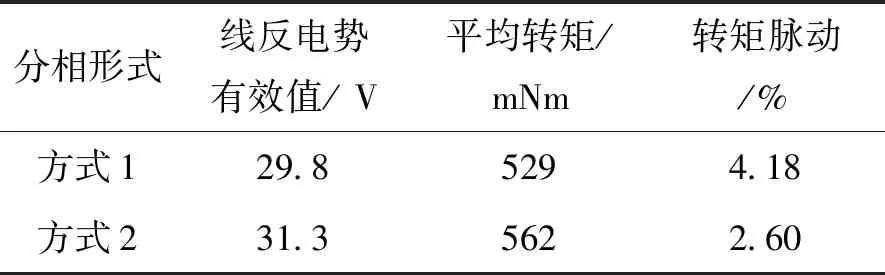
表2 12极39槽电机不同绕组分相方式的转矩脉动
由于极槽配合对无框电机的性能影响很大,因此,在分析12极39槽的基础上,进一步分析10极12槽、14极15槽和14极39槽电机的性能,电机模型如图3所示。不同极槽配合下电机的空载反电动势波形如图4所示,可以看出,14极39槽时,电机的反电动势波形畸变率较低。

图3 不同极槽配合电机模型
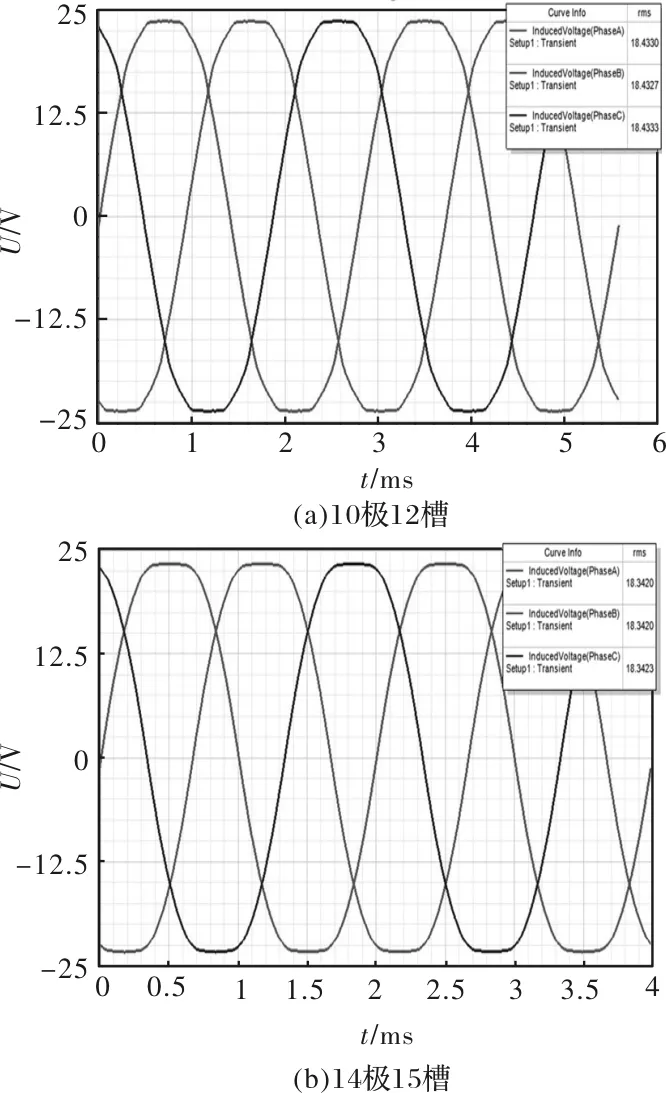

图4 不同极槽配合空载反电动势波形
从表3所示的计算结果可以看出,14极39槽电机在保证平均转矩的同时,转矩脉动很小,具有一定的性能优势。但是电机在14极39槽下的平均转矩不及10极12槽与12极39槽电机大,综合考虑电机的平均转矩与转矩脉动,最终选择的极槽配合为12极39槽。
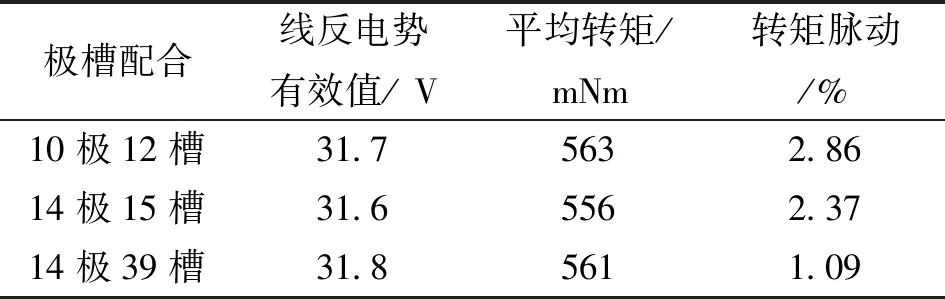
表3 不同极槽配合电机电磁性能对比
3.2 定子斜槽
表4为不同定子斜槽距离对转矩脉动的影响。可以看出定子斜槽可有效削弱齿槽效应对转矩脉动的影响,但同时也会导致电机的基波反电动势和平均转矩产生较大幅度下降。因此,采用斜槽工艺时,需要采取其他措施提高反电动势和平均电磁转矩。
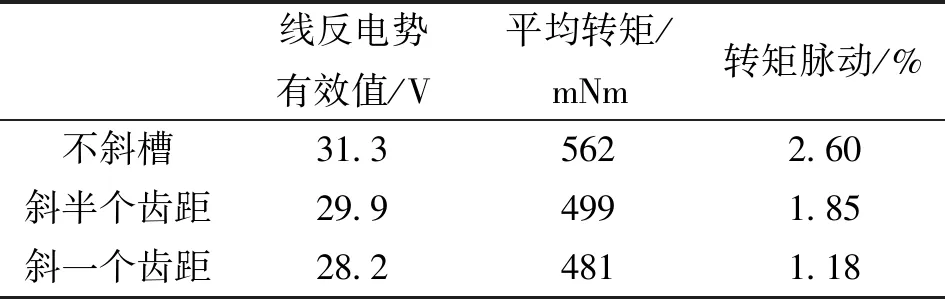
表4 斜槽对空载反电动势和转矩脉动的影响
3.3 定子开辅助槽
在定子齿顶位置开0.5mm的小半圆作为辅助槽以削弱转矩脉动。电机结构如图5所示。
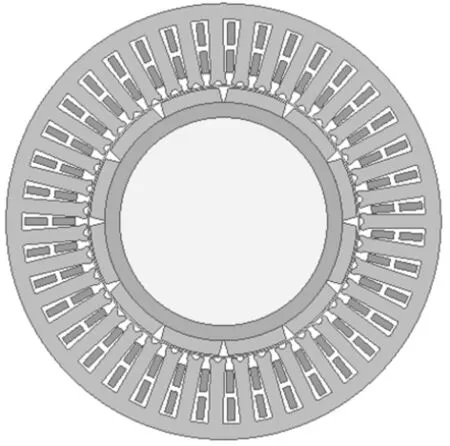
图5 定子开辅助槽结构示意图
从表5所示的计算结果可知,开设辅助槽可以降低转矩脉动0.25个百分点,但同时会使电机的平均转矩下降约2%。

表5 辅助槽对空载反电动势和转矩脉动的影响
3.4 不同转子磁极结构
3.4.1 表面插入式结构对比分析
表面插入式转子磁极结构一方面可以实现永磁体在圆周方向的精确定位,另一方面还可以增大交轴电感,实现一定的凸极效应,可以通过最大转矩电流比控制提高单位电流下的转矩输出,电机结构模型如图6所示。
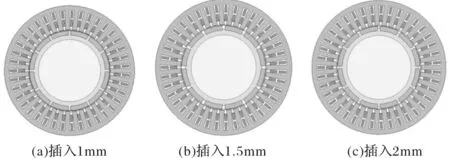
图6 表面插入式转子结构模型
由表6的计算结果可以看出,对于该电机而言,凸极效应对平均转矩影响很小,反而由于极间软磁材料的存在导致漏磁增大导致空载反电动势和平均转矩的下降。

表6 不同表面插入深度对转矩脉动的影响
3.4.2 不等气隙磁极优化
通过优化电机的永磁体磁极形状,利用不均匀气隙实现电机空载气隙磁场波形的正弦分布,从而抑制转矩脉动,不等气隙下电机模型如图7所示。

图7 不等气隙电机模型
从表7所示的计算结果可以看出,采用不等气隙可使电机的转矩脉动降低接近一半,但同时也伴随着电机空载反电动势和平均转矩的降低。由此可见,不等气隙结构可以实现转矩脉动的有效抑制,但要采取其他措施提高电机的平均转矩。
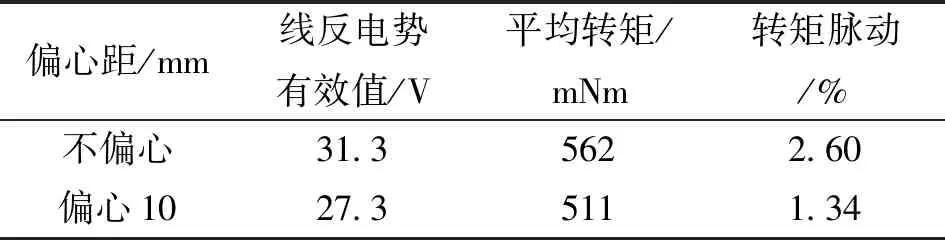
表7 磁极偏心10mm的转矩脉动
3.4.3 磁极偏移
将电机中一半永磁体在原有位置的基础上旋转0.419°得到的偏移之后的电机模型,如图8所示。
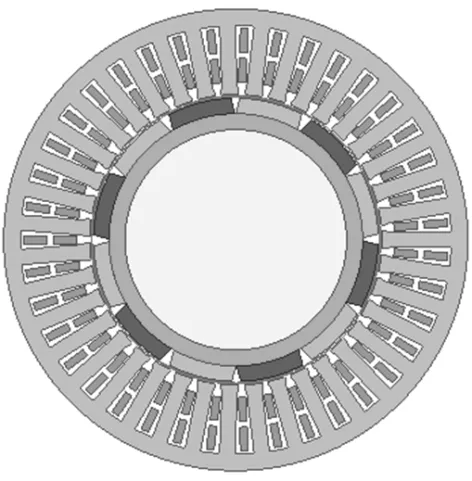
图8 一半磁极偏移示意图
由表8所示计算结果可知,磁极偏移对电机的转矩脉动具有较大不良影响。

表8 磁极偏移对电机性能的影响
3.5 敏感性分析
3.5.1 剩磁密度偏差对电磁性能的影响
在实际电机中采用的永磁材料剩磁密度为1.2T,为研究剩磁密度偏差对电机电磁性能的影响,分别计算了永磁材料剩磁密度为1.18T、1.2T和1.22T时电机的转矩脉动,计算结果如表9所示。从计算结果可以看出,剩磁密度偏差对电机的转矩脉动影响不大。

表9 不同剩磁密度下电机转矩脉动
3.5.2 单块永磁体位置偏差对电磁性能影响
为研究单块永磁体偏差对电机电磁性能的影响,建立图9所示的电机模型。
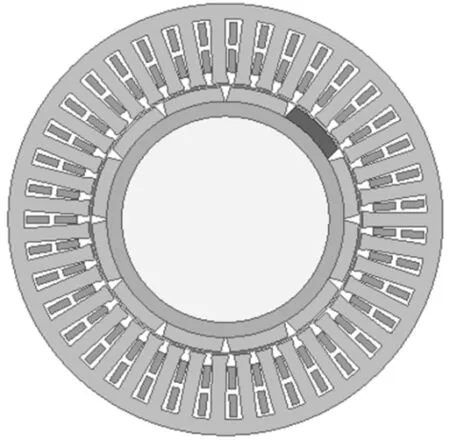
图9 单块永磁体位置偏差示意图
从表10的计算结果可以看出,单块永磁体位置偏差对电机的平均转矩影响不大,但对于转矩脉动却有较大影响。
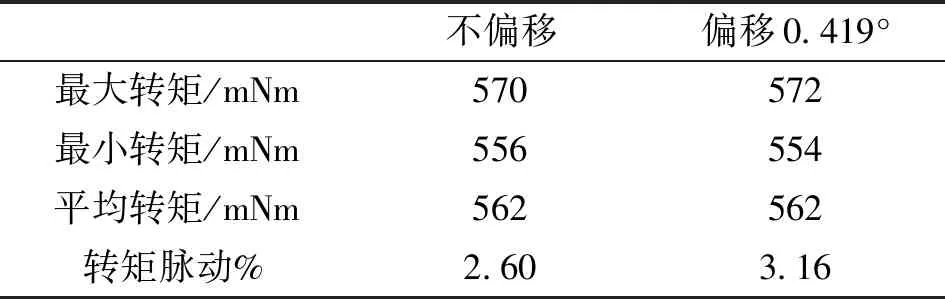
表10 单块永磁体偏移时的转矩脉动
3.5.3 永磁体与转子装配间隙对性能影响
在考虑转子轮毂和永磁体间0.1mm装配间隙的情况下,电机转矩脉动计算结果图表11所示,可以看出电机的平均转矩下降约2.7%,而转矩脉动变化不大。
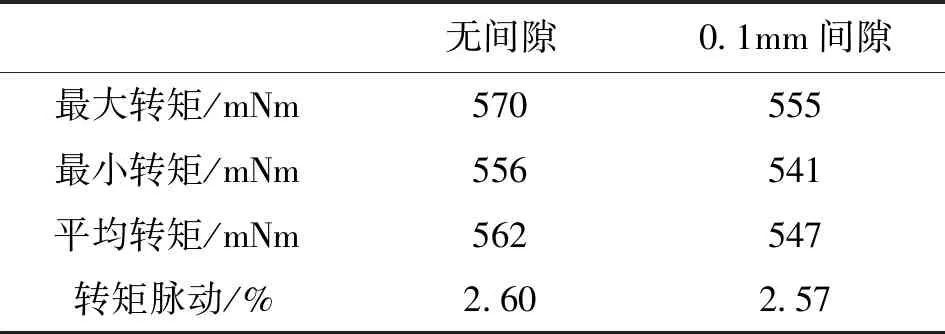
表11 考虑装配间隙时的转矩脉动
4 样机试验验证
为验证以上仿真分析的准确性,将有限元仿真结果与一台118W、4300r/min机器人关节无框永磁同步电动机试验结果进行了比较,样机实物如图10所示。样机的参数如表1所示。该电机在额定转速、额定转矩下的仿真结果如图11所示。

图10 无框电机产品实物图
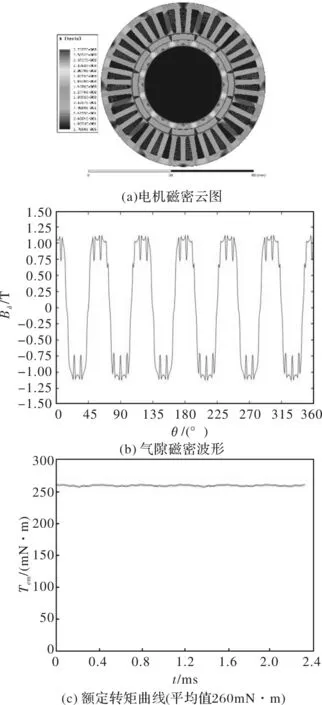
图11 电磁仿真结果
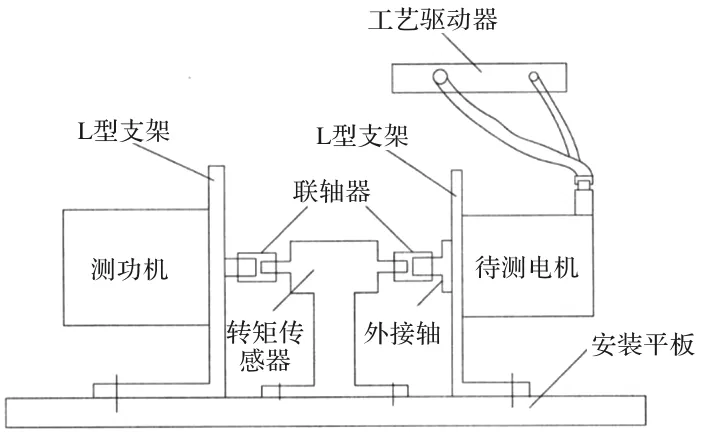
图12 无框电机试验原理图
通过图12所示的试验原理对样机进行了测试,电机在对拖情况下的线反电势实测波形如图13所示。可以看出该线反电动势波形结果与图12(b)所示的仿真结果吻合良好。

图13 无框电机反电势实测图
表12为该电机的详细试验数据与有限元结果对比,可以看出,试验数据与仿真结果吻合良好,验证了仿真结果的准确性,进而验证了转矩脉动抑制方法的有效性。

表12 机器人关节无框电机数据对比
5 结 论
本文针对机器人用关节无框电机的应用特点,分析总结了电机不同结构对转矩脉动的影响,通过优化极槽配合、转子磁极结构等手段降低其齿槽转矩及转矩脉动,改善运行平稳性。并基于这些分析,将有限元仿真结果与一台无框永磁同步电动机样机试验结果进行了比较,验证了转矩脉动抑制方案的有效性。
