基于数值模拟的高压磨料射流喷嘴流场分析及结构优化
2020-06-17郭子豪傅连东
郭子豪,傅连东
(1. 武汉科技大学机械自动化学院,湖北 武汉,430081;2. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)
近年来,高压磨料射流切割技术发展迅猛,相比于最初的纯水射流技术,磨料颗粒具有高硬度与高密度的特点,这使得该技术具有更高的切割效率。执行端喷嘴作为水-磨料高速两相流形成的发生元件,其对切割系统的正常工作和磨料颗粒的加速起着关键性作用。目前,国外针对高压力、高流量液压系统的研发已开展多年,所生产的高压磨料射流切割装备占据全球绝大部分市场份额[1],而国内关于高压/超高压工况下喷嘴内部多相流特性的研究尚处于初期阶段,市场现有的国产磨料射流喷嘴在结构上仍不能够满足高集束性要求,同时喷嘴内壁磨损严重,影响了其服役寿命。已有研究者从喷嘴结构优化(如收缩段角度、混合室长度等)的角度,探索了各结构参数对喷嘴内部射流流场特性的影响,并取得了一定的进展[2-4],但有关磨料入口位置对高压喷嘴内固-液两相流特性影响的研究还报道较少。
基于此,本文利用FLUENT软件对高压磨料射流喷嘴内部的流场进行仿真模拟,重点研究了磨料入口位置对喷嘴内部流场速度分布及喷嘴出口处磨料颗粒束集情况的影响,并提出了减轻喷嘴内部壁面磨损的措施,研究结果可为超高压磨料射流喷嘴的设计与应用提供参考。
1 计算模型的建立
1.1 物理模型
本研究采用市面常见的正交式双向高压磨料射流喷嘴进行模拟,内部结构如图1所示。
高压喷嘴几何模型的建立参照文献[5],由于喷嘴内部细节较为复杂,故适当地进行简化处理(如不考虑对实验结果影响较小的界面间转角处圆角等因素)。图2所示为高压喷嘴中心截面图,图中,L表示磨料入口与收缩区间距(即磨料入口位置),高压水入口内径D1为0.33 mm,磨料入口内径D2为3 mm,混合室内径D3为4 mm,喷嘴出口处内径D4为0.6 mm,喷嘴收缩角θ为27°,混合室长度L1为17 mm,磨料喷嘴长度L2为30 mm,磨料入口过渡区L3为0.5 mm。

1—磨料入口;2—磨料喷嘴;3—高压水入口;4—混合室
Fig.1 Schematic diagram of internal structure of high-pressure spray nozzle
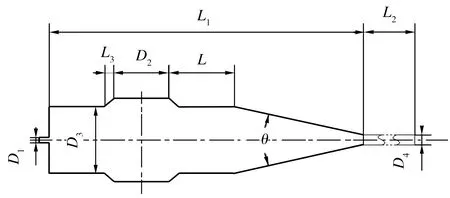
图2 喷嘴中心截面图
根据文献[5]中对磨料颗粒运动轨迹的分析可知,磨料颗粒的运动流线与中心轴线在同一平面内,即磨料颗粒在水流的带动下沿截面向喷嘴尾部运动,然后汇入水流核心,极少会向截面外运动,因此,利用二维截面模型即可得到较为可信的结果。另外,由于喷嘴结构具有对称性,为便于计算,特取模型截面轴对称结构的一半作为计算区域,并用ICEM-CFD软件进行网格划分。图3为以磨料入口位置L=2.5 mm时为例模型的网格划分图,此时网格数目约为90 000,最小网格尺寸约为0.003 mm2。

图3 喷嘴网格划分图
1.2 数学模型
在喷嘴内部,高压水流、磨料颗粒及原先留存的空气会形成多相流。高速水流与空气、低速磨料颗粒之间有速度差,从而形成旋涡,使磨料得以汇入水流核心进而加速。
首先,将喷嘴内水流看作不能压缩的理想液体,可以用Bernoulli方程描述[6]:
(1)
式中:P为流体中某点压强;ρ为流体密度;v为流体该点的速度;h为该点所在高度;C为常数。
出口处水流速度voutlet为:
(2)
式中:C1为出流系数。
流体流动分为层流与湍流两种,可通过雷诺数Re进行判断,Re计算式为:
Re=ρvd/μ
(3)
式中:μ为流体动力黏性系数;d为流体直径。
当Re值高于2300时,流场为湍流状态;Re值低于2300,流场则为层流状态。本研究的高压射流喷嘴中,由于水流速度足够高,计算得知流场为湍流状态,湍流强度I表示为:
I=0.16(ReDH)-1/8
(4)
式中:ReDH为在水力直径DH下的雷诺数。
采用RNGκ-ε双方程模型描述湍流的运动状态[4]:
Gκ+Gb-ρε-YM+Sκ
(5)
(6)
耗散率ε表示为
(7)
式中:κ表示湍流动能;Gκ和Gb分别为由平均速度梯度和由浮力所引起的湍流动能;YM为湍流耗散率,对于不可压缩液体,YM=0;C1ε、C2ε、C3ε为经验常数;σκ和σε分别为湍动能和耗散率对应的Prandtl数,为常数;Sκ和Sε分别为用户定义的源项。
1.3 仿真分析
本研究采用FLUENT软件进行仿真,流场模拟采用RNGκ-ε湍流方程,水相与空气相间采用VOF模型,磨料颗粒使用离散相DPM进行拟合,材料属性参数如表1所示。
边界条件设置:将左侧的高压水流入口设为速度入口,初始速度设定为900 m/s,入口压力约为400 MPa,初始压力为标准大气压(101 325 Pa)。上端磨料颗粒入口为速度入口,设定速度值为0.4 m/s,初始压力为标准大气压。右端磨料喷嘴为压力出口,初始压力为标准大气压。

表1 材料属性参数
求解器设置:压力方程采用PRESTO,其余采用一阶迎风格式,适当调节松弛因子大小,便于模型收敛[7]。同时,为保证仿真结果的精确性,设置各方程残差的收敛数值均为10-6。
2 模拟结果与分析
2.1 混合水相流场
本研究中高压喷嘴内部结构未发生较大变化,仅改变磨料入口位置L对混合水相速度和湍流强度变化趋势的影响不大[8-9],故仅以L=2.5 mm时为例,模型中稳态混合水相流场分布云图如图4所示。

(a)流场速度分布

(b)湍流强度分布

(c)图4(a)中局部放大处的迹线图
Fig.4 Velocity and turbulence intensity distribution diagrams of mixed-water phase
根据喷嘴模型,以中心轴高压水流入口处对应点为原点建立笛卡尔直角坐标系,如图5所示,沿Y轴方向等间距(0.2 mm)取点,范围为0.2~1.8 mm,计算混合水相的速度和湍流强度分布,分别如图6和图7所示。
图6(a)为不同Y偏距下混合水相沿X轴的速度分布情况,可以看出,速度曲线的整体位置随Y值增加呈先降低后升高的趋势,这是由于Y值较小时,此区域即为混合室内高压射流的核心区域,混合水相速度较高,随着Y值的增加,同X坐标值位置处的速度有所降低;然而,高压水流在混合室内中心轴两侧对称的磨料入口处会形成两个旋向相反的旋涡(见图4(c)),这样即可将磨料颗粒卷入高压水流的核心区域,有利于混合相速度的提高。当Y为1.2 mm时,取样区域穿过旋涡中心区域,此时速度曲线位置最低;随着Y值进一步增加,混合水相速度曲线位置逐渐升高。另外,上述4条曲线(Y值范围1.2~1.8 mm)中间段的速度均有所降低,也是由于取样位置经过旋涡时所引起的,在X轴坐标值3~8 mm处,不同偏距混合水相的速度陆续达到最大值。
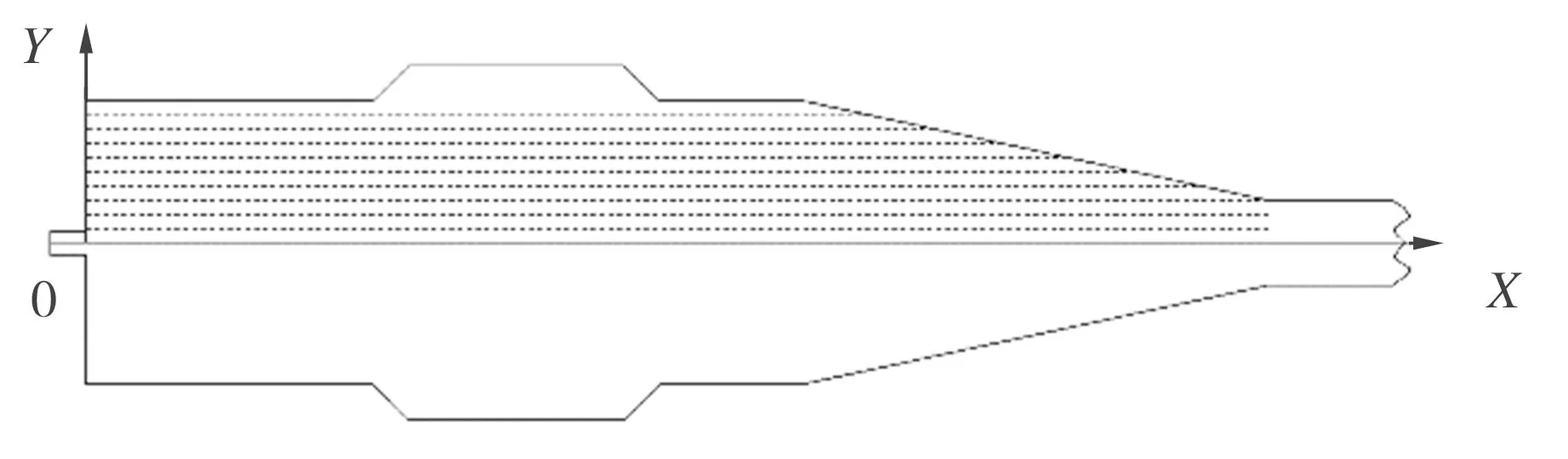
图5 取点位置示意图

(a)不同Y轴偏距
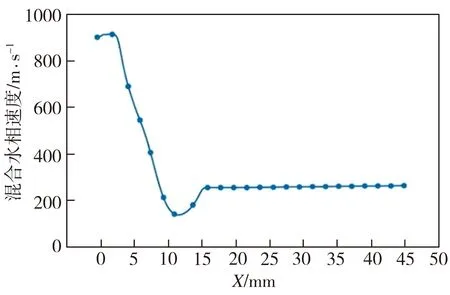
(b) 中心轴线处
由图6(b)所示中心轴线处混合水相的速度分布可见,在中心轴线处,高压射流以900 m/s的速度由水流管进入大直径的混合室内,射流速度迅速降低,并开始与磨料颗粒混合;进入收缩区后,水流开始汇聚,射流速度有所回升,流入长喷嘴后速度逐渐趋于稳定,最终以约262 m/s的速度喷出。
从图7所示混合水相的湍流强度分布情况可以看出,随着偏距Y的增加,湍流曲线位置逐渐下移,亦即相同X坐标值下,混合水相的湍流强度随Y的增加而逐渐降低,并且最大湍流强度随着偏距Y的增加而向X轴正向移动,主要分布在4.2~7.9 mm区间。另外,在中心轴线处,混合水相的湍流强度在混合室内迅速达到最大值118(X坐标值约为5 mm),与磨料充分混合后湍流强度值逐渐降低。

(a)不同Y轴偏距

(b) 中心轴线处
Fig.7 Turbulence intensity distribution of mixed-water phase in nozzle
2.2 磨料颗粒运动分析
2.2.1 磨料在喷嘴处的收束性和速度
以图2所示模型为基础,改变磨料入口位置L进行仿真,L取值范围为0.5~4.5 mm,每隔0.5 mm取一个值进行模拟,当磨料入口位置在混合室最右端时,L即为最小值0.5 mm。由于模型为沿X轴的对称结构,故只对喷嘴出口处界面上半部的磨料颗粒数密度进行统计,不同磨料入口位置L下出口处磨料颗粒数密度的分布情况如图8所示。由图8可见,当L取0.5 mm时,喷嘴出口处磨料颗粒的体积分数分布较为分散,各位置处磨料颗粒数密度相对较低;随着L值的增加,磨料颗粒分布开始变得集中,且逐渐向中心轴线附近聚集,当L为2.5 mm时,磨料颗粒分布最靠近中心轴线处,相比于其他条件,此时喷嘴中磨料颗粒的收束性最好;随着L值继续增加,出口处磨料颗粒数密度分布偏距逐渐增大,收束性降低。
图9所示为L分别为0.5、2.5、4.5 mm时出口处磨料颗粒的体积分数分布图,可以清楚地观察到不同L取值下出口处磨料颗粒的分布情况。

(a)L=0.5 mm (b)L=1.0 mm
(c)L=1.5 mm

(d)L=2.0 mm (e)L=2.5 mm
(f)L=3.0 mm

(g)L=3.5 mm (h)L=4.0 mm
(i)L=4.5 mm
图8 喷嘴出口处磨料颗粒的数密度分布
Fig.8 Number density distribution of abrasive particles at nozzle outlet

(a)L=0.5 mm (b)L=2.5 mm
(c)L=4.5 mm
图9 喷嘴出口处磨料颗粒的体积分数分布图
Fig.9 Volume fraction distribution diagrams of abrasive particles at nozzle outlet
图10所示为不同磨料入口位置L下喷嘴出口处磨料颗粒及混合水相的平均速度变化情况。由图10可见,当L为0.5 mm时,出口处磨料颗粒和水射流的速度均相对较低;随着L值的增大,磨料和混合水相速度均显著提高,当L取2.5 mm时,磨料颗粒速度达到最大值252.32m/s,此时水流相速度为262.14 m/s,随后两类速度均略有减小。

图10 喷嘴出口处混合水相与磨料颗粒的平均速度变化
Fig.10 Average velocity change of mixed-water phase and abrasive particles at nozzle outlet
综上所述,对于本文所建立的喷嘴模型,当磨料入口位置L取2.5 mm时,出口处磨料颗粒的速度和收束性均达到最佳,因而具有较高的切割效率;结合上述分析还可知,此时磨料入口处两相流的湍流强度较大。由此可见,磨料入口处湍流强度越大,越易于磨料在喷嘴混合室内与水流相的混合及加速。
2.2.2 磨料入口处壁面的磨损分析
不同磨料位置L条件下,磨料入口靠后的壁面上磨料颗粒的体积分数分布情况如图11所示,磨料颗粒最大体积分数随L的变化见图12。由图11可见,由于受流场旋涡的影响,磨料入口靠后的壁面上会受到大量磨料颗粒的撞击,故此处磨料颗粒体积分数最高,磨损也最大;随着L的增大,磨料颗粒聚集位置先沿磨料入口方向上升,而后下降。
结合图12可知,随着磨料入口越接近高压水流入口(即L值的增加),磨料颗粒的最大体积分数呈现持续升高的趋势;当L取5.5 mm时,磨料颗粒集中于磨料入口与上壁面的交界处,并且相比于其他条件,磨料颗粒的体积分数也相对最高,因而可能对喷嘴结构造成较大磨损[10]。就磨损方面考虑,L不宜取较大值。
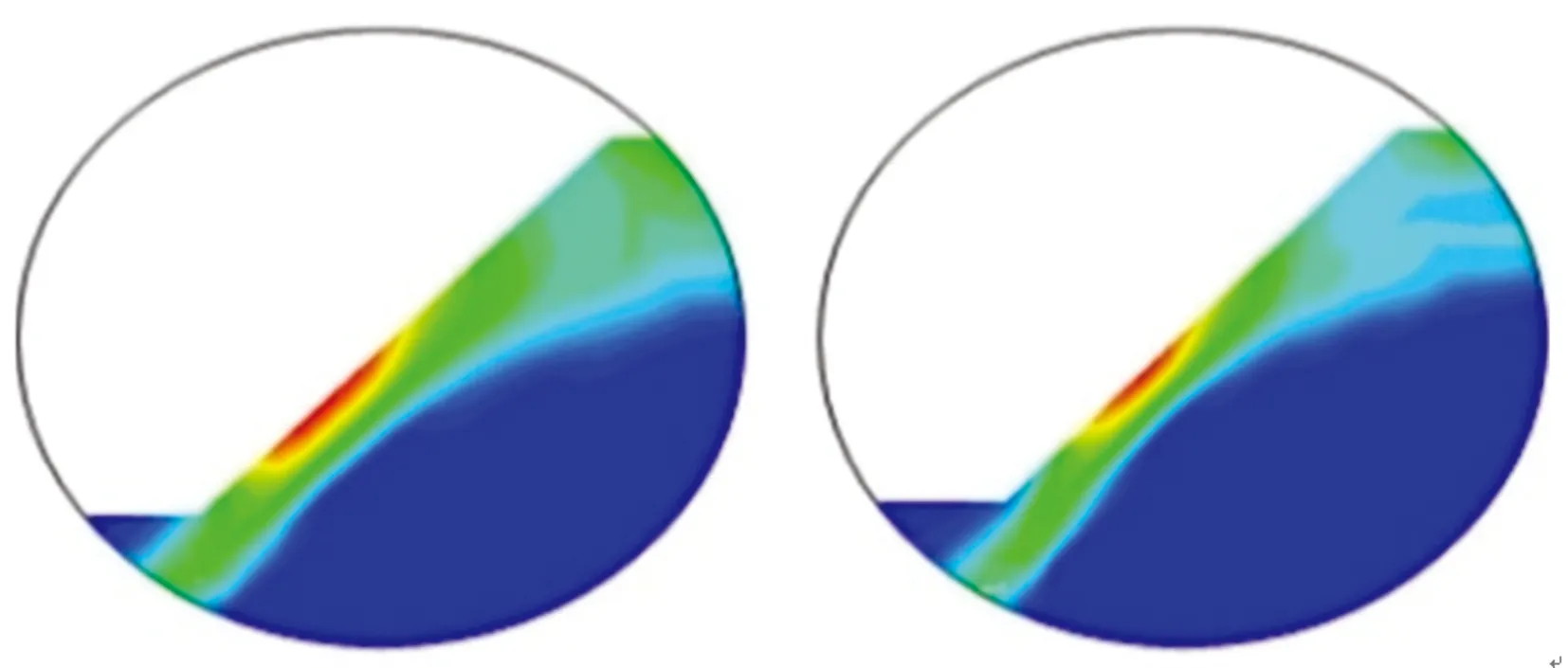
(a)L=0.5 mm
(b)L=2.5 mm

(c)L=4.0 mm
(d)L=5.5 mm
图11 磨料入口后壁面磨料颗粒的体积分数分布图
Fig.11 Volume fraction distribution diagrams of abrasive particles at rear wall of abrasive inlet
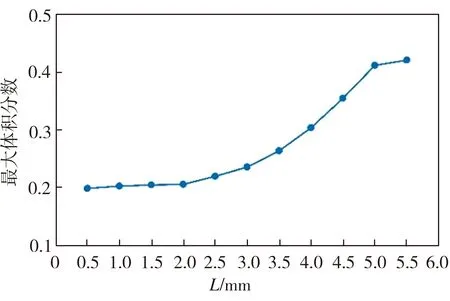
图12 磨料入口壁面处磨料颗粒最大体积分数变化
Fig.12 Maximum volume fraction change of abrasive particles at rear wall of abrasive inlet
2.2.3 圆角过渡对喷嘴内部流场的影响
当磨料入口处于靠近高压水入口位置时,磨料颗粒在旋涡作用下会向喷嘴后向下方运动,此时磨料颗粒可能会撞击高压水入口壁面,导致后壁面磨损。为解决该问题,本文通过在混合室和磨料入口区域应用圆角过渡设计来抑制小旋涡的形成。以磨料入口位置L取5.0 mm时为例,未采用圆角过渡设计以及过渡区圆角半径R分别为1.0、1.5 mm时的仿真结果分别如图13和14所示。
由图13所示的磨料颗粒体积分数分布云图可见,高压水入口的后壁面与上下壁面间由于没有圆角过渡,此区域会有小旋涡形成,使磨料卷入并撞向后壁面,进而加剧后壁面的磨损。由图14可见,当圆角半径R为1.0 mm时,上壁面与后壁面转角处的旋涡明显减小,撞击至后壁面的磨料颗粒的体积分数大幅降低;随着R增大至1.5 mm,上壁面与后壁面转角处的旋涡几乎消失,磨料颗粒流迹已经不与后壁面相撞,磨料可以正常汇入水流核心。另外,对于没有圆角过渡结构的喷嘴而言,磨料入口与上壁面交界处的磨料体积分数最大值为41.2%,当过渡区圆角半径R为1.0、1.5 mm时,该交界处磨料颗粒体积分数最大值依次为29.3%和26.4%,由此可见,圆角过渡设计有助于减轻喷嘴磨料入口与上下壁面交界处的磨损情况。

(a)磨料体积分数迹线图
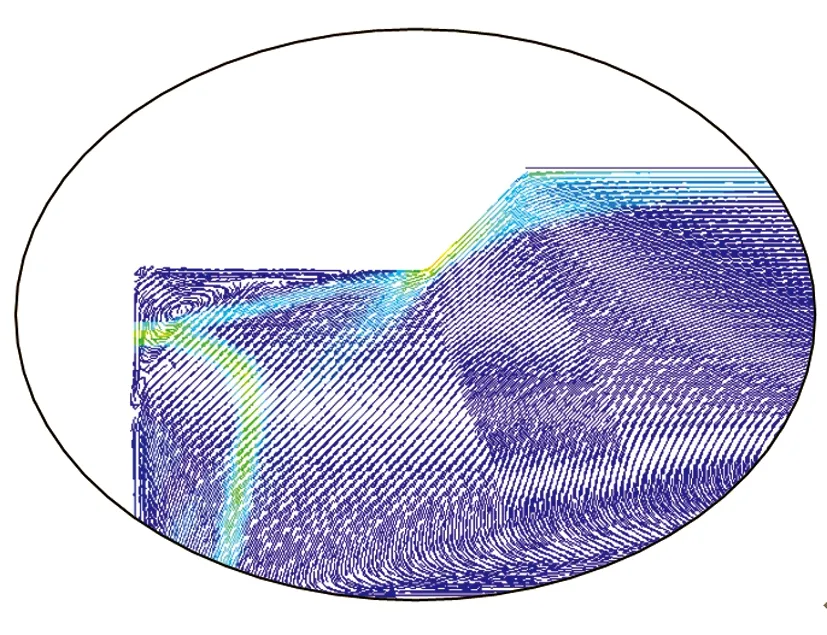
(b)局部放大处的迹线图
Fig.13 Volume fraction distribution diagrams of abrasive particles in nozzle without round-corner transition

(a)R=1.0 mm
(b)R=1.5 mm
图14 不同圆角半径下磨料入口附近磨料颗粒的体积分数分布图
Fig.14 Volume fraction distribution diagrams of abrasive particles near abrasive inlet with different transition radius
3 结论
(1)随着距喷嘴中心轴线距离(偏距)的增加,高压喷嘴内部混合水相的湍流强度逐渐降低,但由于在磨料入口处存在旋涡,混合水相速度则随之先降低后升高,并且不同偏距对应的混合水相的速度和湍流强度沿X轴向会陆续达到最大值后再下降。
(2)高压喷嘴内混合水相速度流场核心上、下均有旋涡,可将磨料卷入水流核心,磨料水射流得到加速,当磨料入口距离收缩区间距L为2.5 mm时,磨料入口处湍流强度相对较大,越易于磨料在喷嘴混合室内的混合与加速,此时高压喷嘴的切割效率最佳。
(3)当磨料入口位置越靠近高压水入口时,磨料颗粒集中位置沿磨料入口壁面先上移再下移,本模型中,当L取5.0、5.5 mm时,磨料颗粒集中于磨料入口与上壁面交界处,该处磨料颗粒的体积分数随着L值的增加逐渐升高,此条件下喷嘴内壁面磨损较为严重。可以通过在喷嘴入口后壁面和上下壁面之间采用圆角过渡设计,从而起到改善射流流向和减少聚集处磨料颗粒体积分数的作用。
