位置扰动型电液力加载系统反步控制

魏 航，金晓宏,2，黄 浩,2，陶 平

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

电液负载模拟器可用于在地面上复现飞行器的舵面在空气中所受的力[1]，其核心部分是电液力加载系统，它依据被加载的位置系统的位移变化对其实时施加相应的力。由于位移是主动动作，施力系统的加载是被动动作，因此，位置系统对电液力加载系统的位移扰动会产生多余力，从而影响力加载系统的输出精度。鉴于力加载系统的非线性特性，设计控制器来提高系统对加载指令的跟踪性能具有很大难度[2]。

为了抑制加载系统的多余力，国内外研究人员提出了多种方法，大致可分为两类：①结构补偿，如利用阀芯反向运动的电液伺服阀补偿[3]、增加阻尼耗能装置[4]、位置同步校正[5-6]等；②控制补偿，如模型自适应控制补偿[7]、神经网络控制补偿[8]等。上述方法有一定的可取性，但实际操作中仍有局限性。结构补偿会使系统结构更为复杂，可靠性降低，而且提高了系统的能耗；控制补偿的信号采集实现起来较为困难。

本文则采用反步控制方法，除伺服阀部分以外皆运用非线性方程来构建力加载系统的模型，基于Lyapunov稳定性原理设计一次反步控制器，以期有效解决电液力加载系统中由于位置扰动而产生的多余力问题以及控制信号难以实现的问题。

1 位置扰动型电液力加载系统描述

力加载系统是电液负载模拟器的重要组成部分，用于对位置系统施力，但其运动过程会受到位置系统的位置干扰，故控制器的设计目标是使加载系统的输出力尽可能地精确跟踪任意指定的加载指令。电液力加载系统的结构如图1所示，其主要由电液伺服阀、阀控液压缸、控制器和力传感器这四部分组成。在控制器的设计中，力反馈、运

图1 位置扰动型电液力加载系统结构示意图

Fig.1 Schematic diagram of electro-hydraulic force-loading system with position disturbance

动反馈以及压力反馈(通过压力传感器)都是可以获得的[9]。

力传感器的刚度远大于活塞杆刚度，可以忽略力传感器的变形，传感器检测出的力即为加载系统输出力F：

(1)

式中：K为液压缸活塞杆结构刚度，N/m；xp为位置系统活塞位移，m；xf为力加载系统活塞位移，m；m为活塞及负载折算到活塞上的质量，kg；B为黏性阻尼系数，N/(m/s)；A为液压缸控制腔活塞的有效面积，m2；pL为负载压力，Pa。

电液伺服阀采用零开口四边滑阀，阀口开度可用xv表示，伺服阀阀口流量q1和q2为：

(2)

(3)

式中：Cd为薄壁小孔流量系数；w为阀口面积梯度，m；ρ为液压油密度，kg/m3；ps为供油压力，Pa；p0为回油口压力，Pa；p1为液压缸右腔C1的压力，Pa；p2为液压缸左腔C2的压力，Pa；定义s(*)为：

(4)

鉴于采用的是高性能电液伺服阀，同时为了便于控制器设计，可以将电液伺服阀和放大器增益看作一个比例环节，因此有：

Kamp=i/u

(5)

Ksv=xv/i

(6)

式中：Kamp为伺服放大器增益，A/V；Ksv为电液伺服阀增益，m/A；i为电液伺服阀输入电流，A；u为力加载系统输入电压，V。

(7)

(8)

图1中液压缸活塞杆向右移动取为正方向。假定液压缸没有外泄漏，液压缸各工作腔内压强处处相等，当活塞杆被迫向右移动时，xv≤0，油液通过伺服阀阀口流入液压缸右腔C1，流量为q1，且流量连续性方程为：

(9)

式中：Cip为液压缸内泄漏系数，(m3/s)/Pa；V1=V01-Axf表示右腔C1的容积，m3，其中V01为右腔C1的初始容积，m3；Ee为油液的有效体积弹性模量，Pa。

流入液压缸左腔C2的流量为q2，且流量连续性方程为：

(10)

式中：V2=V02+Axf表示左腔C2的容积，m3,其中V02为左腔C2的初始容积，m3。

将式(1)、式(7)～式(10)整理可得：

(11)

式中：R1和R2为有向流量，分别为：

(12)

(13)

2 反步控制器的设计

反步控制理论的主要思想是将一个复杂的高阶系统拆解成若干个阶数较低的子系统，然后从最终控制量所在的子系统开始依次对每个子系统设计虚拟控制器，直到输入子系统结束，系统的最终控制信号是通过一系列虚拟信号以递归的方式得到[10]。为了信号易获取、控制器易实现，本研究采用一次反步的设计。首先简化方程，定义

α1=(R1/V1+R2/V2)AEeg，

α3=(1/V1+1/V2)AEeCippL，

则式(11)可写为：

(14)

令e=F-Fd为输出力的跟踪误差，其时间导数为：

(15)

式中：Fd为期望输出力。

因此，可设计反步控制器u使得跟踪误差e能收敛到零或者一个很小的值，且具有确定的稳态性能[11-12]。所设计的控制器为：

(16)

式中：k为反步系数，一经取定便为常数。

基于控制器式(16)，定义如下的李雅普诺夫函数L(t)：

(17)

函数L(t)对时间的导数为：

(18)

将式(16)代入上式，得到：

(19)

3 仿真研究

为检验反步控制器的性能，根据位置扰动型电液力加载系统的数学模型，利用MATLAB/Simulink软件建立系统的数值仿真模型，如图2所示，仿真程序中电液伺服阀采用文献[3]中的二阶振荡环节。

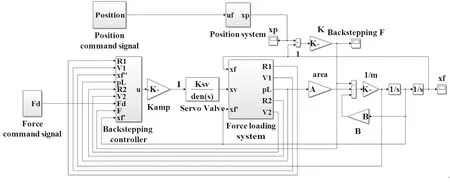
图2 加入反步控制器的电液力加载系统Simulink模型

采用ode45算法，设置步长为0.001 s，计算相对误差取1×10-6。采用典型的电液力加载系统参数(见表1)，考虑到实际系统中要保证液压缸没有内漏也没有外漏，且电液伺服系统的综合阻尼比通常为0.05～0.08，所以为了更有效地评价控制方法的性能，仿真中特意将黏性阻尼系数取为文献[3]中的综合黏性阻尼系数，其值为0.1 N/(m/s)。

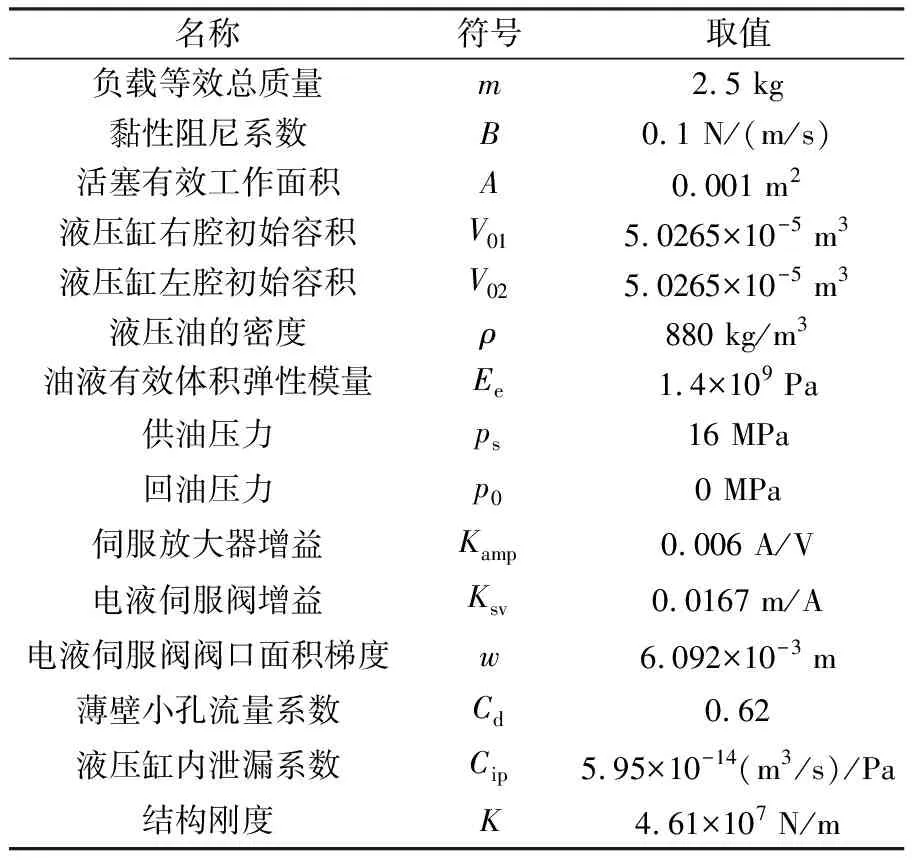
表1 电液力加载系统参数

在位置扰动下，力加载系统被动运动，液压缸会产生大量的强迫流量从而引起多余力，为了更好地跟踪加载指令，所设计的控制器需将强迫流量放出。为了检验本控制器在受到位置扰动时是否能真正做到将被迫流量放出，特进行以下仿真：取反步系数k=200，力加载系统阶跃输出力为5000 N，在0.2 s处加入不同程度的阶跃位置扰动，得到伺服阀阀口开度变化情况如图3所示，阀口开度参数如表2所示，阀口流量特性曲线如图4所示。

由图3和图4可知，力加载系统在0.2 s受到位置扰动时，阀口反向运动，右腔C1变为回油腔来排油，以此将强迫流量排出，左腔C2变为进油腔，补充流量；随着位置扰动的增大，强迫流量增多，阀口反向开度必须增大以排出更多的强迫流量。由表2可知，位置扰动从0.0005 m增大到0.004 m时，阀口反向开度也由7.6 μm逐渐增大到58.8 μm。

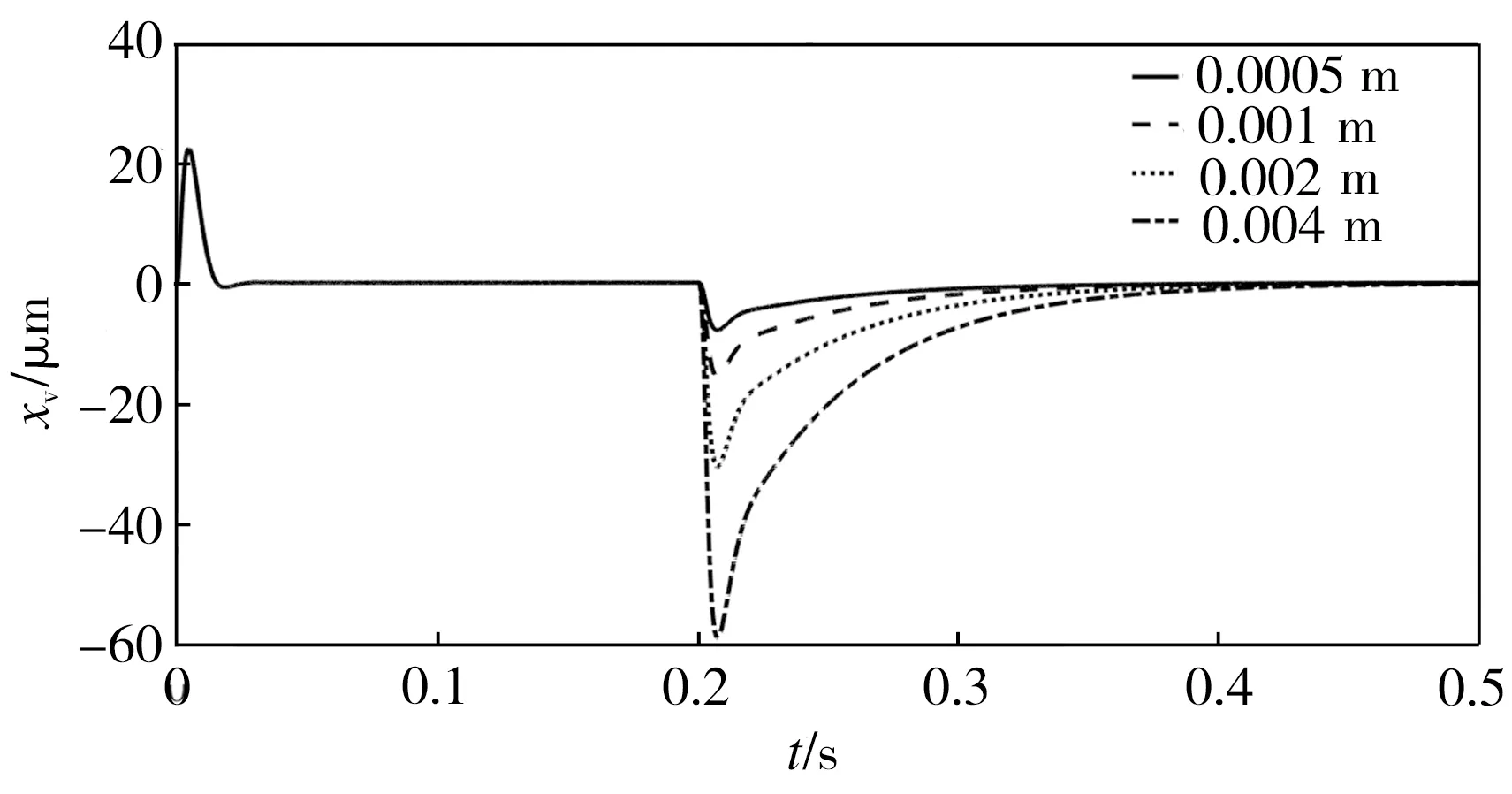
图3 不同程度位置扰动下的阀口开度

表2 阀口开度参数

图4 不同程度位置扰动下的阀口流量

为了探究反步系数k值对控制器的影响，分别取k为50、200、400，对位置扰动xp=0.001×sin(2πt) m、输出幅值为5000 N的阶跃力进行仿真，结果如图5所示，系统响应特性如表3所示。从图5和表3可以看出，随着k值从50增至400，输出力的上升时间tr从0.0384s逐渐减少到0.0037 s，稳态误差ess也从0.5 N减至0.07 N，但是输出力的最大超调量Mp却从1 N增大到956 N。为了兼顾稳态误差和响应速度，并使最大超调量不至于过大而造成系统冲击、设备损坏，综合权衡之后，以下的仿真中k值均取200。

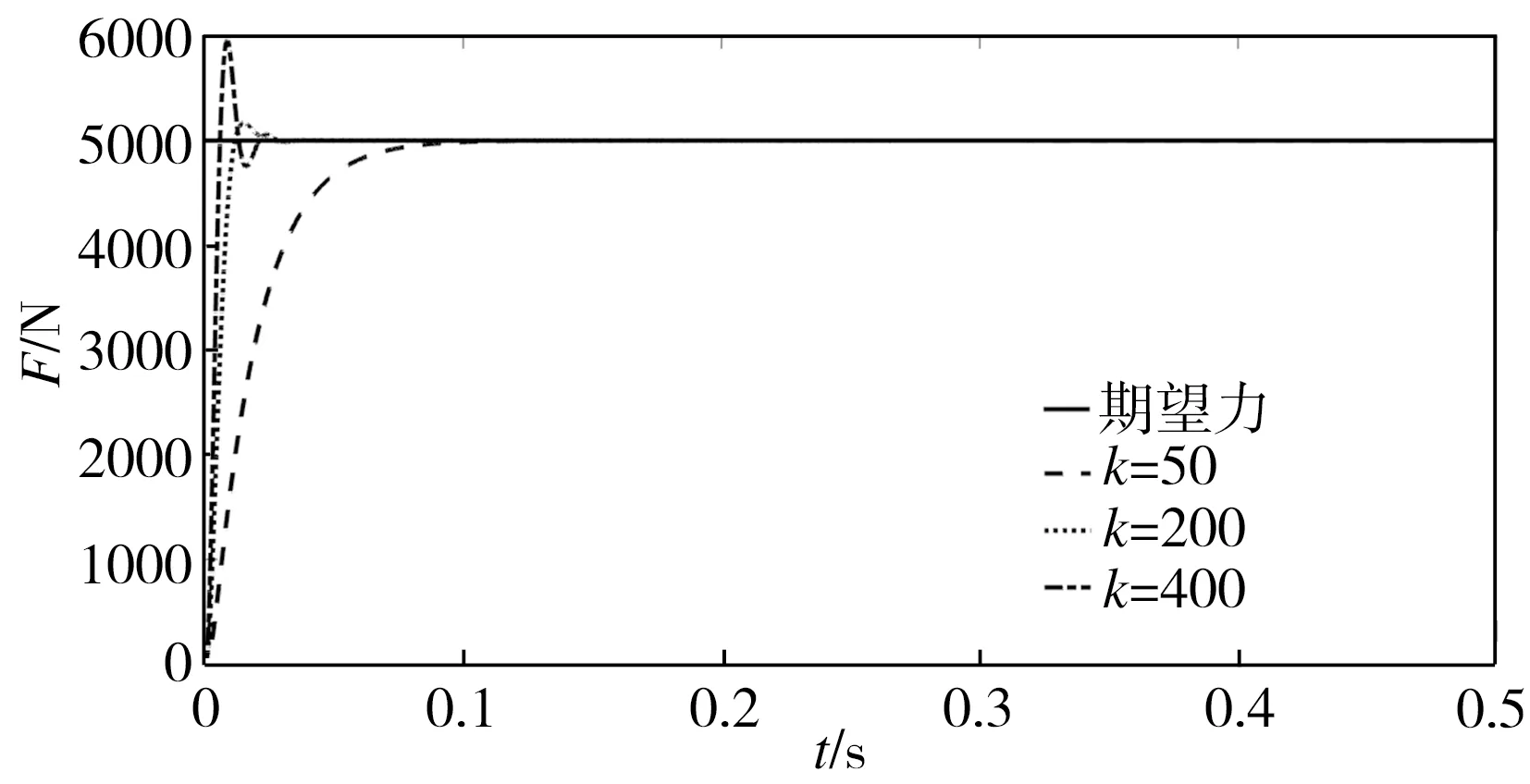
图5 反步控制器取不同k值时的系统输出力F

Fig.5 Output forceFof the system with backstepping controller at differentkvalues

表3 反步控制器取不同k值时的系统响应特性

Table 3 Response characteristics of the system with backstepping controller at differentkvalues

ktr/sMp/Ness/N500.038410.52000.00711740.134000.00379560.07

为了进一步检验所设计的反步控制器对力加载系统加载指令的跟踪效果，下面在多种加载工况下输出阶跃力，将反步控制器和传统PID控制器进行性能对比仿真分析。

首先，在系统运动初始时加入位置扰动xp=0.01sin(2πt) m。PID控制的力加载系统参数取值：kp=2，ki=20，kd=0.003；反步控制力加载系统参数取值：k=200。二者均输出幅值为5000 N的阶跃力，仿真情况如图6所示，系统响应特性如表4所示。

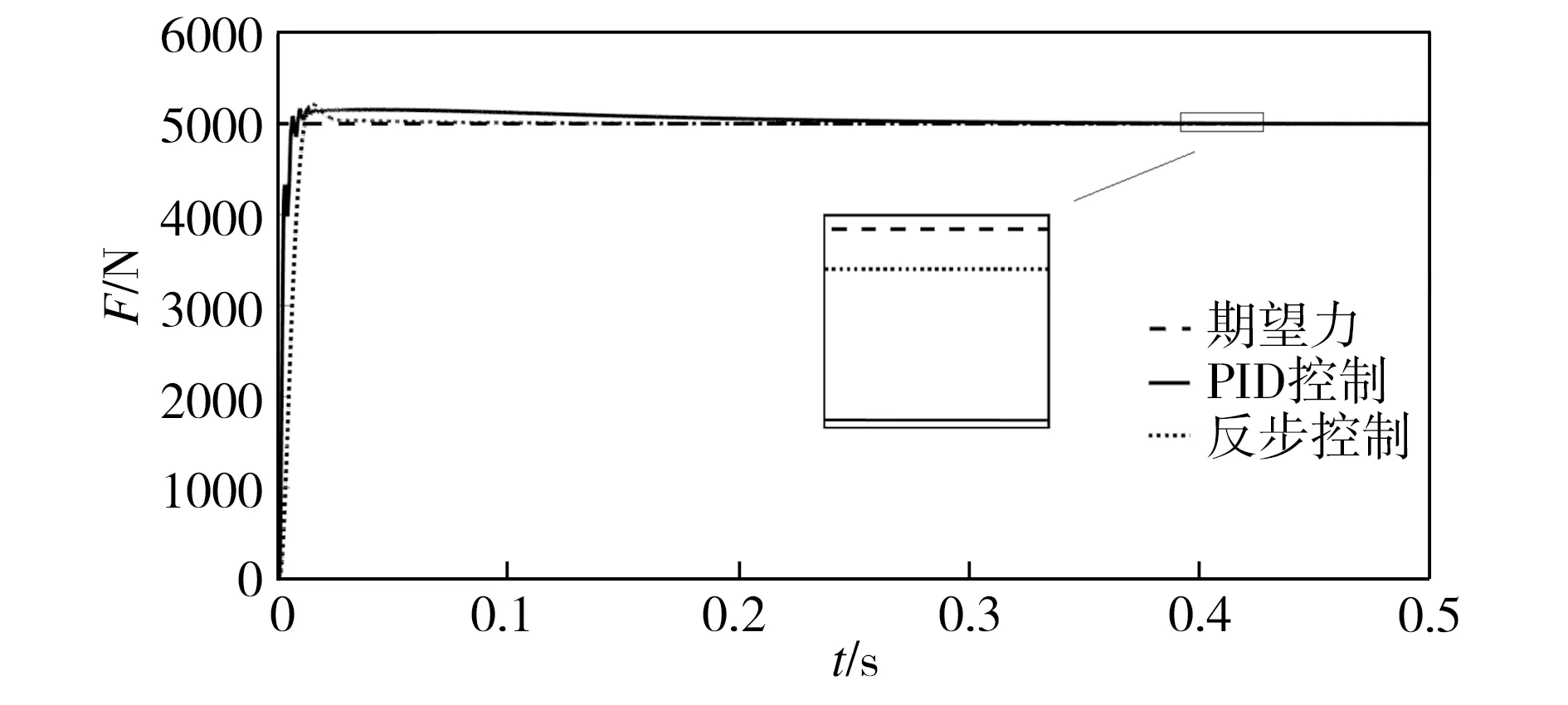
图6 正弦位置扰动下采用不同控制器的系统输出力F

Fig.6 Output forceFof the system with different controllers under sinusoidal position disturbance

表4 正弦位置扰动下采用不同控制器的系统响应特性

Table 4 Response characteristics of the system with different controllers under sinusoidal position disturbance

从图6和表4可以看到：力加载系统在受到正弦位置扰动后，PID控制下系统输出力的上升时间tr以2.8 ms的微弱优势领先，且其超调量Mp比反步控制系统的Mp少50 N，但是PID控制的力加载系统达到1%的稳态误差用时t为0.207 s，而反步控制系统仅用时0.024 s，其响应速度更快； PID控制力加载系统的最大跟踪误差ess达到12.1 N，而使用反步控制器时，系统的ess仅为2.5 N，稳态误差小很多。

然后，在力加载系统运动初始时加入幅值为0.05 m/s的斜坡位置扰动，PID控制和反步控制的力加载系统均输出幅值为5000 N的阶跃力，仿真结果如图7所示，系统响应特性如表5所示。

从图7和表5中可以看出：PID控制力加载系统输出力的上升时间tr以2.4 ms的微弱优势领先，系统在受到斜坡位置扰动带来的多余力影响之后，其最大超调量Mp超过反步控制力加载系统的Mp有58 N；PID控制的系统达到1%的稳态误差用时t为0.356 s，而反步控制力加载系统仅用时0.0984 s，响应速度更快；PID控制力加载系统的ess达到0.1 N，而反步控制力加载系统的ess仅为0.005 N，稳态误差更小。

图7 斜坡位置扰动下采用不同控制器的系统输出力F

Fig.7 Output forceFof the system with different controllers under ramp position disturbance

表5 斜坡位置扰动下采用不同控制器的系统响应特性

Table 5 Response characteristics of the system with different controllers under ramp position disturbance

控制器tr/st/sMp/Ness/NPID0.0040.3564800.1反步0.00640.09844220.005

为了检验所设计的控制器对正弦力加载指令的跟踪性能，在位置扰动xp=0.03sin(4πt) m时，要求系统分别输出Fd=2000sin(4πt)+3000 N、Fd=2000sin(10πt)+3000 N的不同频率正弦力，对PID控制和反步控制的力加载系统进行仿真比较，输出力和跟踪误差的仿真情况分别如图8和图9所示。

由图8(a)和图9(a)可见：在输出2 Hz的正弦力时，对于正弦位置扰动产生的较大多余力，PID控制消除多余力的作用并不明显，尤其是在波峰、波谷的位置，多余力的存在影响了力加载系统的跟踪性能，误差达到了5.12%；而反步控制器对位置扰动产生的多余力有很好的消除效果，加入该控制器后的力加载系统获得了非常好的跟踪性能，且过了0.05 s初始阶段后，跟踪误差逐渐收敛至很小的范围，最大误差仅为1.32%。

(a) 2 Hz

(b) 5 Hz

图8 不同控制下系统输出的不同频率正弦力F

Fig.8 Sinusoidal output forceFwith different frequencies of the system with different controllers

(a) 2 Hz

(b) 5 Hz

图9 不同控制下系统输出的不同频率正弦力F的跟踪误差

Fig.9 Error of sinusoidal output forceFwith different frequencies of the system with different controllers

由图8(b)和图9(b)可见：在输出5 Hz的正弦力时，PID控制器对于力加载指令的跟踪效果更加恶化，在波峰、波谷的位置，多余力的存在使得力加载系统的跟踪误差高达5.75%；而反步控制力加载系统的跟踪性能依然十分优秀，过了0.06 s初始阶段后，跟踪误差逐渐收敛至很小的范围，最大误差仅为1.93%。

4 结论

(1) 加入反步控制器的力加载系统受到位置扰动时，系统中的电液伺服阀阀口反向运动，进油腔变为回油腔来排油，以此将强迫流量排出，减少多余力，而且位置扰动越大，阀口反向开度也越大。

(2) 反步控制器的反步系数k值越大，系统响应越快，经过初始阶段后的跟踪误差也越小，但超调量会相应增加。

(3) 在位置扰动下，相较于PID控制，本文设计的反步控制加载系统输出的阶跃力最多经过0.0984 s就能准确跟踪阶跃力加载指令，响应速度更快；输出阶跃力最大误差不超过2.5 N，稳态误差更小；输出正弦力时，最多经过0.06 s的初始阶段后就能更精确地跟踪加载指令，且之后能一直保持良好的跟踪性能，最大误差不超过1.93%。