船舶主动减振器安装位置选取和设备选型

吕志庆，黄金林，高占峰

（中远海运重工有限公司设计研究院，辽宁大连 116024）

0 引言

船体梁振动是船舶振动形式中危害最大、最难解决一种。船体梁振动不仅带动生活区的晃动，还影响了船员与乘客的舒适度，甚至可能影响船舶的疲劳寿命，威胁到船舶的安全。尤其低阶船体梁振动，频率低、振幅大，该振动形式的出现表明该船沿船长方向的刚度设计与主机选型不匹配。局部的结构形式修改和重量布置调整对船体梁振动几乎无效，只有通过减小振源的方式才能有效的降低该振动产生的危害。

主机垂向不平衡力矩是引起船体梁振动的一种常见激励，如图1所示。通常，MAN的主机可以通过在主机前后两端安装偏心轮的方式（常作为主机合同中的备选项）抵消该力矩，而瓦锡兰主机多数无法安装偏心轮，需要外接主动减振器。通过主动减振器产生一个与主机不平衡力矩频率相同的力，以抵消主机不平衡力矩的影响。

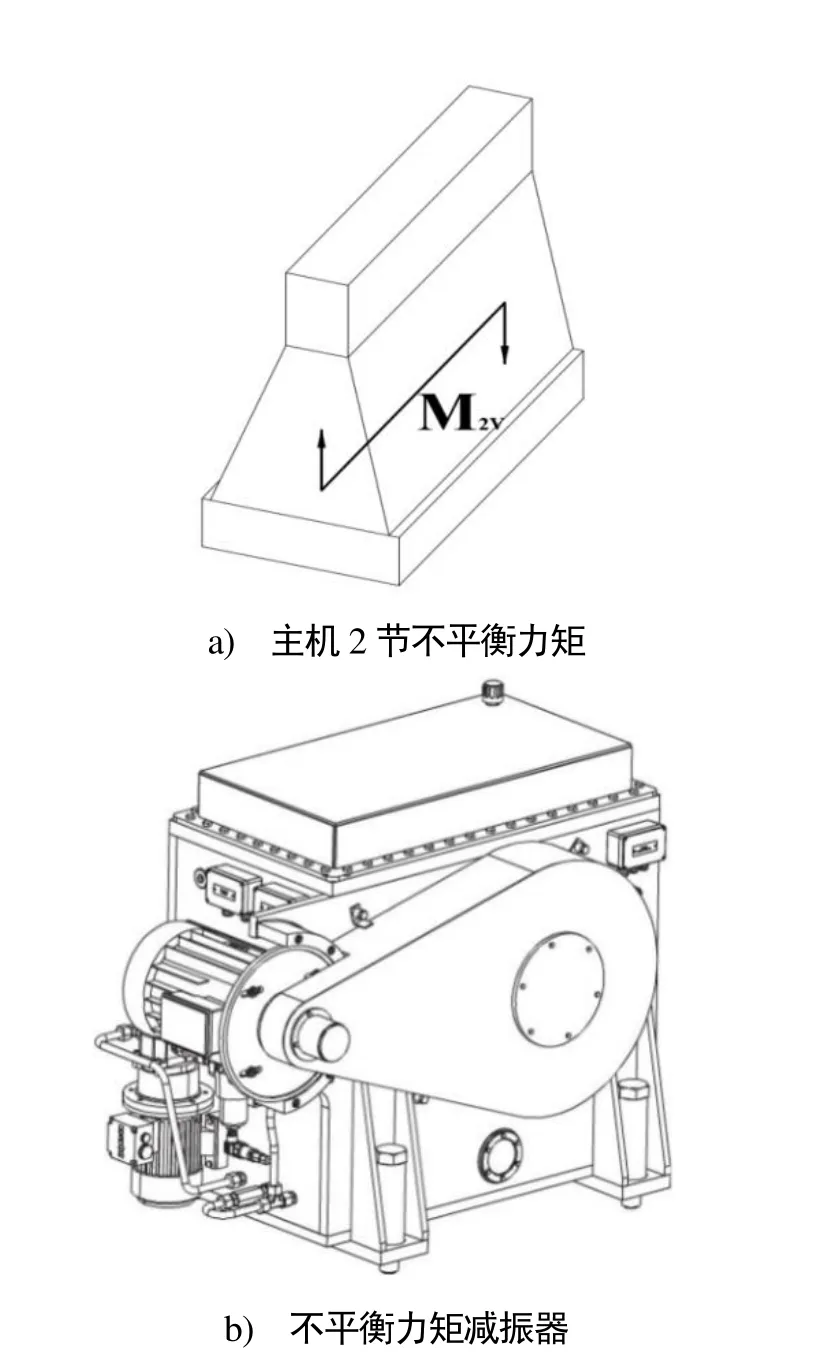
图1 主机2阶垂向不平衡力矩和不平衡力矩减振器

本文从船体梁受迫振动的机理出发，推导船体梁振动发生的理论依据，并探索振动对外界激励位置的敏感程度，进而得出一系列关于减振器安装位置、选型和减振效果的结论，并采用有限元法进行验证，最后在某集装箱实船项目中进行验证。

1 伯努利梁受迫横向振动机理研究

1.1 伯努利梁受迫振动求解

忽略阻尼影响，伯努利梁弯曲振动的运动方程为[1-2]

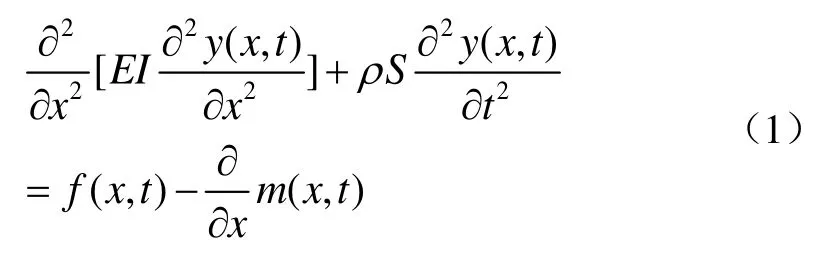
式中：f(x,t)为外界作用力；m(x,t)为外界作用力矩。

采用分离变量法，方程解的形式为

式中：φ(x)为梁的振型；q(t)为随时间变化的振幅。

已知伯努利梁的自由振动固有频率和振型，采用模态叠加法计算梁受迫振动方程（1）的解。令

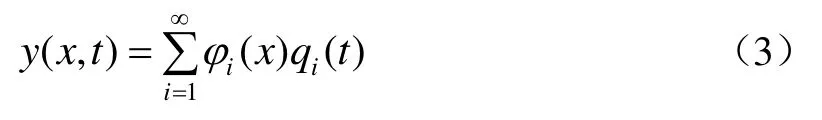
将式（3）代入式（1）可得

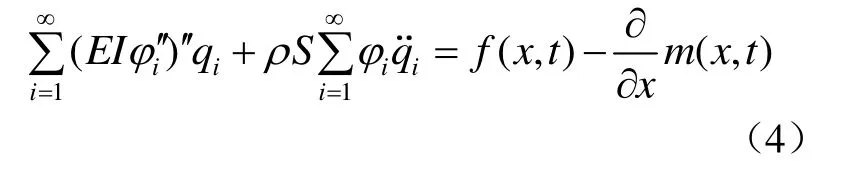
方程（4）两边乘φj并沿梁长对x积分得

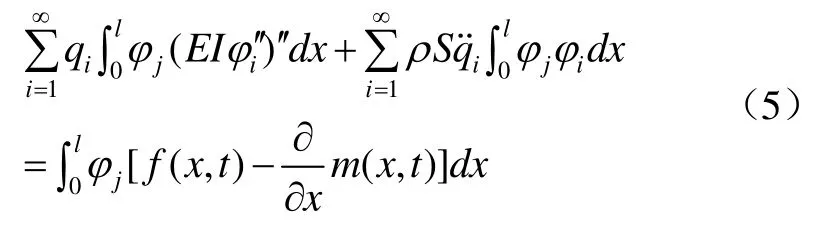
根据模态函数的正交性，上式可转化为

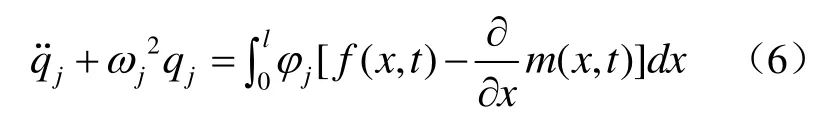
根据分部积分

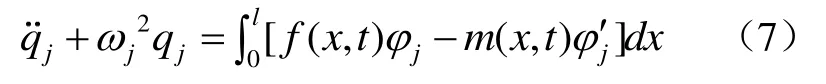
假设伯努利梁在x=x1处受集中力F(t)，在x=x2处受集中弯矩M(t)，此时上式可用δ函数表示为分布形式

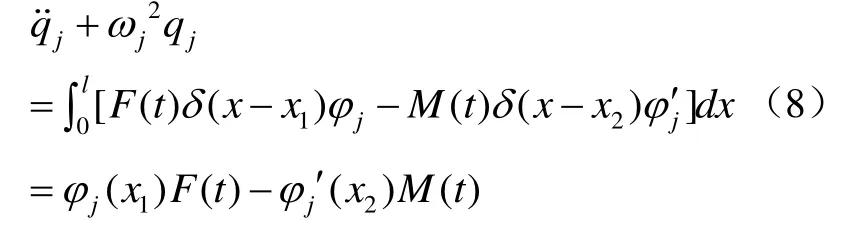
对公式（8）采用杜哈梅尔积分[3,4]

将式（9）带入式（3）得最终响应为

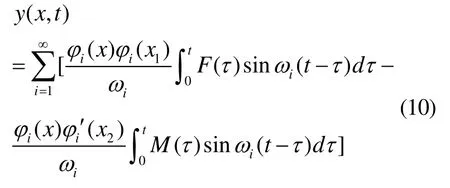
1.2 受迫振动响应分析

式（10）即为伯努利梁受迫振动的振动响应表达式，其中第一项为某点受集中力作用的响应，第二项为某点受集中力矩作用的响应。对式（10）进行分析

1）若伯努利梁仅在x=x1处受动态集中力作用，且外力的激振频率与第j阶固有频率相等，即发生共振，根据模态正交性原则，将式（10）转化为

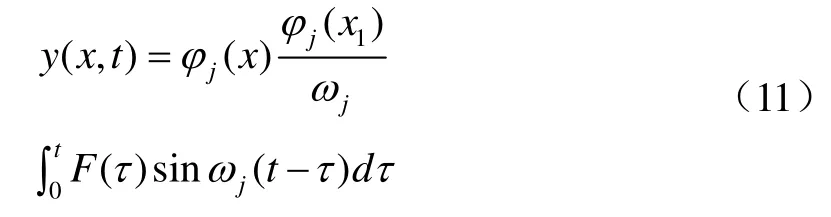
式中：φi(x)、ωi均为梁的固有属性，当激振力幅值和激振频率确定时，振动响应值仅取决于φi(x1)的值，即激振力在梁上的作用位置x1。由式（11）可知，当激振力作用于模态φi(x)的节点时，φi(x1)=0，振动无法被激起；当激振力作用于模态φi(x)的波腹时，φi(x1)最大，此时振动响应最大。

2）若伯努利梁仅在x=x2处受动态集中弯矩作用，且外力矩的激振频率与第j阶固有频率相等，即发生共振，根据模态正交性原则，将式（10）转化为

同理，振动响应值仅取决于φi'(x2)的值，即该梁第j阶振型在点x2处的斜率，最终取决于激振弯矩在梁上的作用位置x2。由式（12）可知，当弯矩作用于模态φi(x)的波腹时，φi'(x2)=0，振动无法被激起；当弯矩作用于模态φi(x)的节点时，φi(x2)最大，此时振动响应最大。

3）若伯努利梁在x=x1处受到动态集中力作用，同时在x=x2处受集中弯矩的作用，如图2所示，且力和弯矩的频率相等（均与第j阶固有频率相等），根据模态正交性原则，可将式（10）转化为

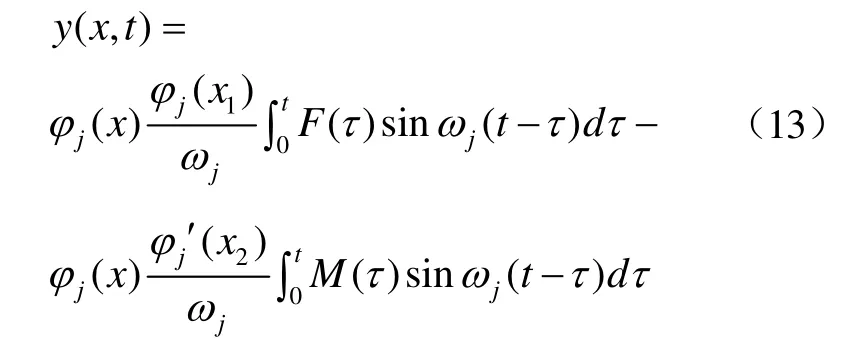
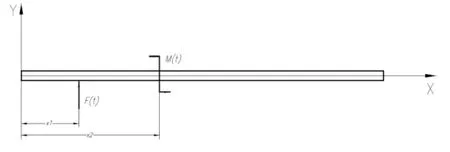
图2 伯努利梁同时受集中力和集中力矩

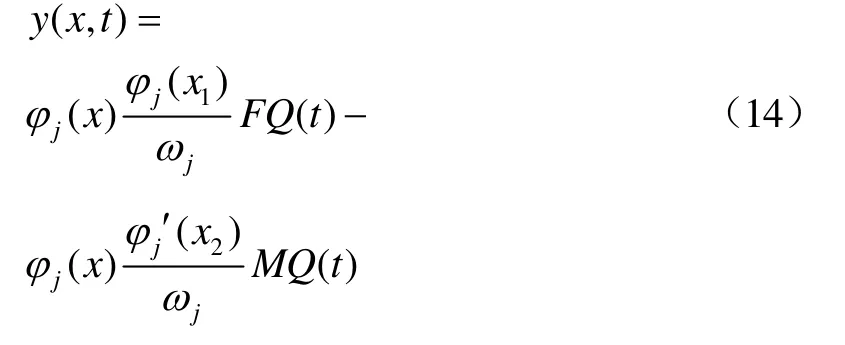
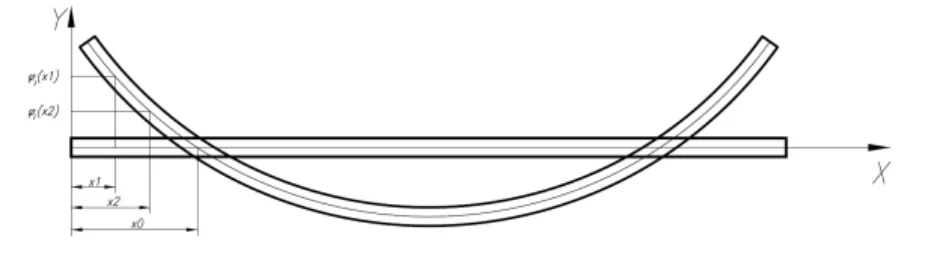
图3 自由伯努利梁一阶振型

图3为自由梁的一阶振动模态，当外界激励作用位置目标振型斜率变化不大时，带入式（15）可得

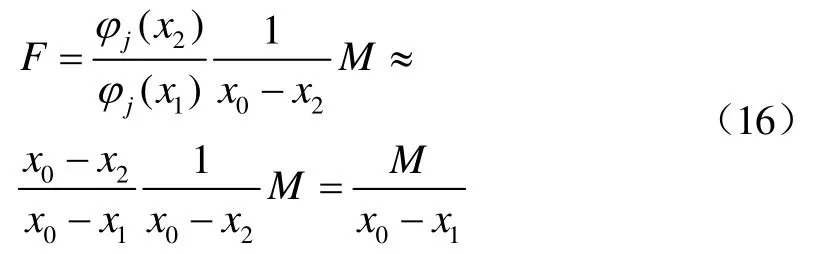
可见，当外界集中力幅值与集中弯矩幅值满足式（16）的关系时，伯努利梁振动响应为0。

1.3 小结

1）外界激振力作用在伯努利梁某阶振型的节点时，无法激起该阶振型；作用在某阶振型波腹处或自由端处时，振动响应最大。因此，减振器若安装在目标振型的节点处将无法生效，应尽量安装在波腹处或自由端。

2）外界激振力矩作用在伯努利梁某阶振型的波腹处时，无法激起该阶振型；作用在某阶振型节点处时，振动响应最大。因此，从减振角度考虑，应尽量将主机布置在接近目标振型波腹，并远离节点的位置。

3）当伯努利梁上同时作用频率相等的集中力和集中弯矩，且力和弯矩的幅值满足式（16）所示的关系时，振动响应可以抵消。此结论可作为减振器激振力幅值的计算依据。

2 有限元算例验证

采用有限元法对上述结论进行验证，计算某自由梁的固有频率，并在梁上不同位置分别施加集中力和弯矩，采用谐响应法计算梁上某点的响应值，绘制频率响应曲线，对比分析以验证1.3节中的结论。

图4 一维梁模型以及前3阶振型

算例中的目标振型取第二阶振型，对应固有频率为20.485 Hz，如图4所示。计算6种工况，按表1所示，分别在梁的不同位置施加力和弯矩，采用谐响应法计算同一点（本算例中取梁的右端点）的频率响应曲线，进行比对。

图5～图7为6种计算工况下梁右端点的频响曲线，观察20.485Hz对应的响应值，即图4中第二阶振型对应的响应值，可见图5～图7分别验证了1.3节中的3条结论。

3 实船验证

本文1.3节的结论在实船主动减振器的安装过程中有非常实际的指导作用，可作为减振器选型和安装位置选择的依据。某小型集装箱船采用了瓦锡兰的 6缸主机，该主机在 NCR工况下存在1400kN·m 的二阶垂向不平衡力矩，且该船的船体梁二阶垂向振动固有频率大约2.35Hz，如图8所示，与主机常用转速72转/分钟下的主机二阶激振频率接近，存在共振风险。进一步计算该船在主机二阶垂向不平衡力矩作用下的振动响应，发现生活区的振动存在超标风险，考虑增加主机二阶主动减振器以抵消主机二阶垂向不平衡力矩造成的结构振动。

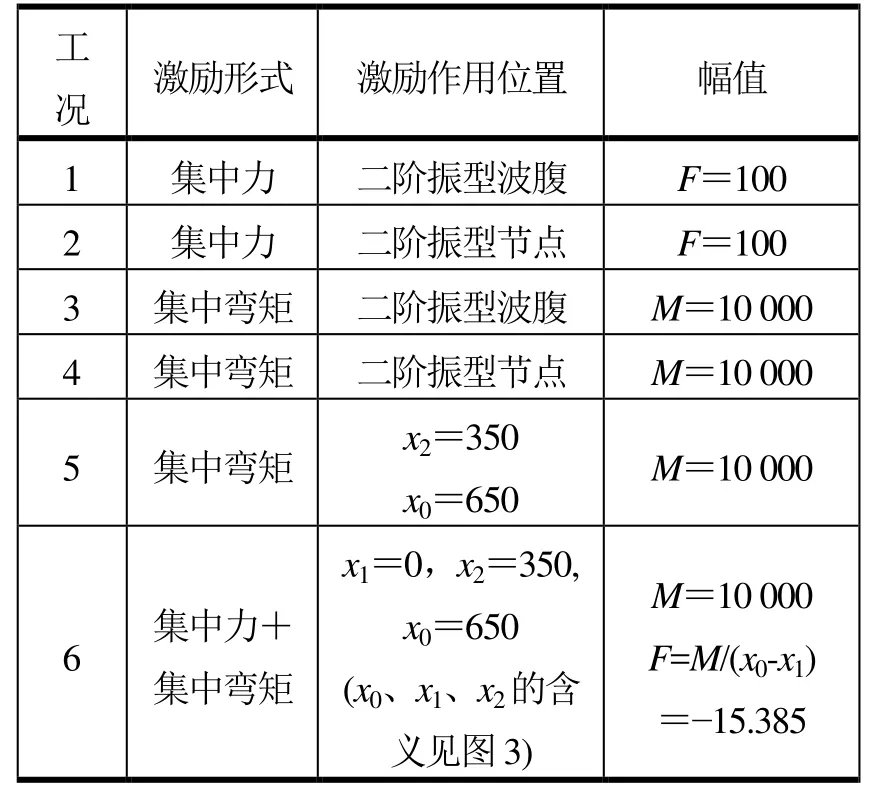
表1 6种计算工况

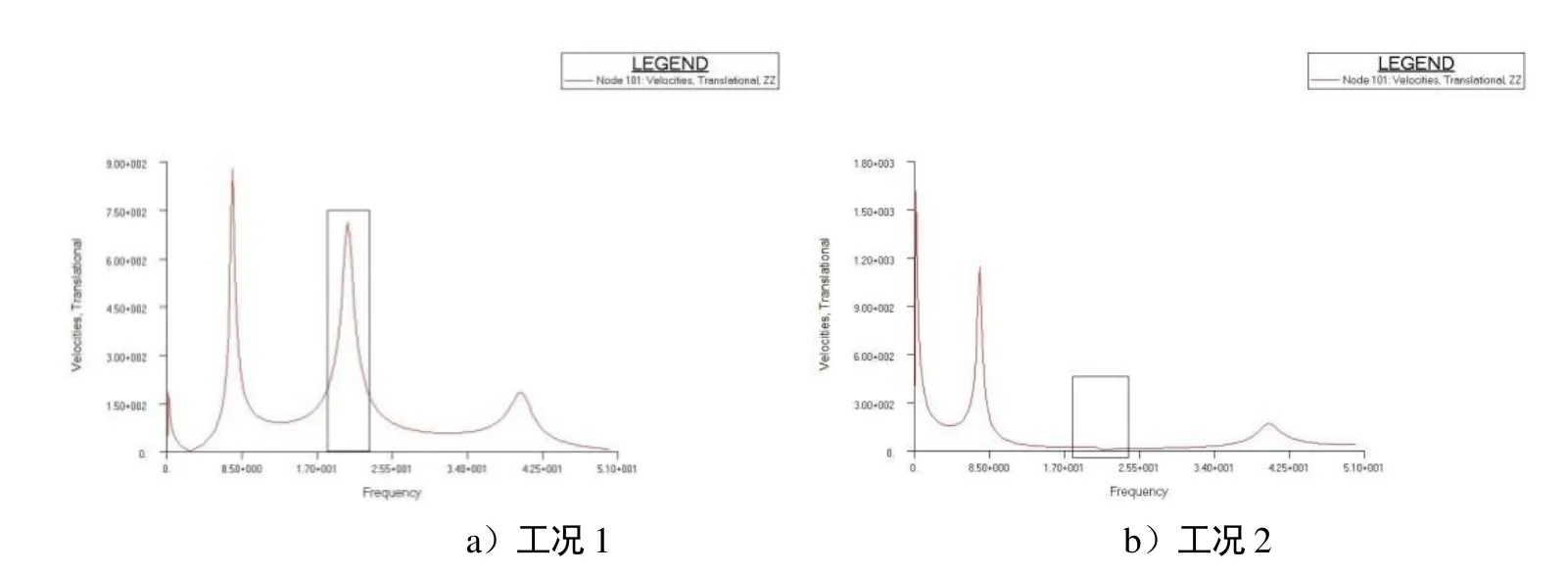
图5 工况1和工况2下自由梁上某点的振动频响曲线

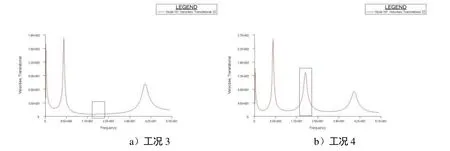
图6 工况3和工况4下自由梁上某点的振动频响曲线

图7 工况5和工况6下自由梁上某点的振动频响曲线

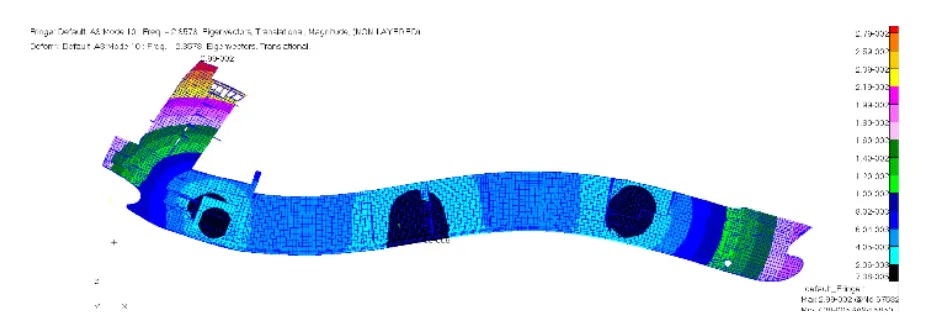
图8 某小型集装箱船船体梁三阶垂向振动

根据1.3节中的结论3），减振器安装位置离振动节点越远，需要的激振力越小；再充分考虑实船的空间布置和刚度搭配等因素，最终确定将减振器安装在舵机舱内，如图9所示，根据式（16）计算得出的激振力幅值53kN。

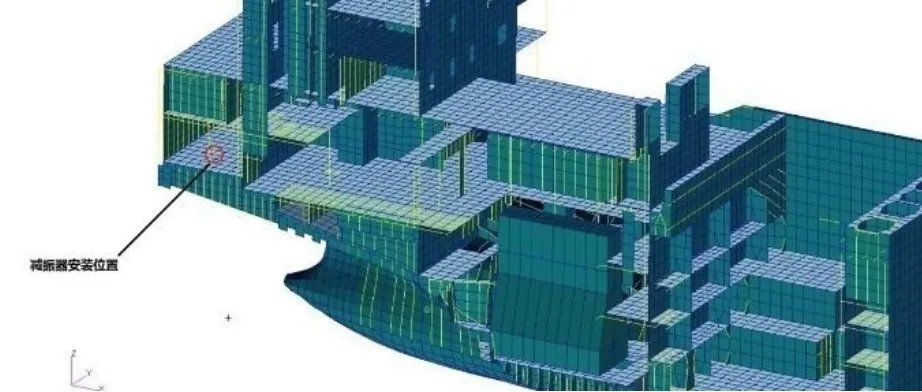
图9 减振器安装位置

分别计算安装二阶减振器前后的船舶振动响应，在驾驶甲板上取同一测点，绘制其振动频响曲线[5,6]，对比2种工况下的振动响应值，如图10所示。由此可见，安装减振器前，在 2.35Hz附近,频响曲线存在明显的共振峰，且振动速度幅值超过20mm/s；安装减振器后，2.35Hz附近的共振峰明显被削弱，振动速度幅值被减弱到了5mm/s以下，效果明显。

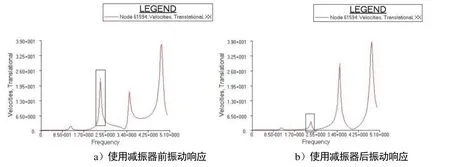
图10 使用减振器前后驾驶甲板某测点振动响应曲线

4 结论

本文采用自由伯努利梁模拟自由船体梁，通过对其受迫振动机理的研究，得出了梁的振动响应与激励形式和激励位置间的关系，提出了3条在船舶减振设计中具有指导作用的结论。采用有限元法分别对其进行了验证，并在实船项目中证明了该结论的有效性。从作用机理上明确减振器安装位置对减振效果的影响，为船厂设计减振器的选配和安装位置提供理论指导依据。