船体分段下胎封固支撑位置优化算法的研究
2020-06-15张雪彪宋志鹏
鹿 想,张雪彪,宋志鹏
(大连理工大学 运载工程与力学学部 船舶工程学院,辽宁大连 116024)
0 引言
在现代造船工艺中,分段建造完成之后,需要采用吊装的方式将其放置在托架上,托架上布置钢墩和木锲等结构,将分段支撑起来,此道工序称为下胎封固。图1是下胎封固后的分段由盘车移运的过程,根据建造计划的要求,盘车将分段连同托架运输到合适的工位,开展后续的装配工作。分段在下胎封固完成之后,由于分段在托架上由有限个支撑点支持,为了避免可能发生的变形,以及保证分段运输过程中的稳定性,分段托架和支撑点的合理设计成为下胎封固设计中的关键环节。

图1 盘车运输分段实况图
船体分段下胎封固工艺简单,精度控制技术也相对粗糙,该工艺不仅对分段下胎后的预舾装作业产生影响,而且由此产生的分段结构变形也会对后续的涂装和装配工艺带来负面影响:1)由于分段放置在托架上,会增加预舾装作业的施工难度,由于托架与分段之间的高度限制,导致部分舾装件无法安装,需要留待分段涂装结束后在总组/合拢场地继续施工,进而对船体涂装也造成了破坏;2)下胎封固后如果有局部的变形会影响船体结构精度;3)下胎封固区域在分段涂装时无法涂漆,其中以外板为胎的双斜切类型分段受影响最大,需要考虑如何在不影响船体结构精度和分段下胎后预舾装工作的前提下,优化下胎封固工艺及工装设备,以减少下胎封固工艺对船体涂装的影响。
在实际的工艺设计过程中,船厂设计人员一般都是根据经验来进行分段的下胎封固方案设计,很少有人专门研究这些问题;其中分段下胎封固工艺所导致的船体结构局部变形会影响分段结构精度,这主要与下胎封固点的选择密切相关,封固点的选择与分段吊装工艺中吊点的选择有相似之处,都是为了减少变形、提高结构的稳定性。吴仲其等[1]提出了船舶分段吊装的工艺要求和注意事项,芮晓松等[2]基于有限元仿真软件建立15 000 DWT化学品船机舱分段的弱框架结构有限元模型,在计算过程中仅考虑重力,以施加惯性载荷的方式计算得到该分段在吊装翻身过程中最大拉应力和最大剪应力,为求解下胎封固过程中的分段变形可以提供参考。林少芬[3]将最小眼板数量作为优化目标,验证了粒子群算法求解船舶分段吊装方案设计问题的可行性;李瑞等[4]对船舶分段吊装方案设计系统进行了研究,引入粒子群优化算法,并借助MATLAB和ANSYS软件的数据交互,实现吊点位置的最优化设计,这些研究将优化算法引入了吊装的方案优化中。
目前下胎封固支撑点的设计还没有成熟的算法,本文主要研究下胎封固支撑点的设计,基于工程经验,本文确立了分段下胎封固的一般工艺要求和工艺原则,下胎封固支撑点的计算选用随机行走优化算法,利用MATLAB软件进行编程实现,其中的结构变形计算模块则通过ANSYS软件进行计算,最后以一个双层底分段为例进行了算法验证,初步实现了下胎封固方案设计的自动化。
1 船舶分段建造下胎封固工艺简述
1.1 下胎封固结构介绍
图2为某船上甲板分段下胎封固方案设计图,为了避免结构变形,在分段上端设有局部的临时加强槽钢。船体分段有平面分段和曲面分段,平面分段形状规则,重心较低,下胎封固比较简易。对于曲面分段,需要综合考虑重心以及运输过程中的稳定性等因素,封固工艺相对复杂。下胎封固方案设计要结合不同分段的特点,本文旨在开发支撑点设计的优化算法,研究对象主要是结构相对简单的平面双层底分段。

图2 某分段下胎封固设计图
1.2 支撑结构简述
托架与分段之间的支撑结构有:1)方形钢墩,尺寸为300 mm×400 mm×400 mm,钢墩与分段之间的接触面垫有胶皮;2)对扣槽钢,对于特殊的曲面分段,将槽钢与分段焊接在一起,保证其稳定性,一般采用28A槽钢对扣焊接的方式。支撑位置一般设置在强力构件交叉点处。
托架对整个分段起承载作用,采用2个托架进行支撑。托架和分段的总重量不能超过盘车运输时候的承载力,托架位置设置在强力连续构件下方。某船厂常用的托架规格类型有承载能力为100 t、60 t、40 t、20 t这4种,各型号托架的主要区别是承载力,所以分段的重量是影响托架型号选择的主要因素。在布置托架时要考虑运输盘车的载荷分布曲线,盘车中间区域的承载能力较强,托架应放置在中间区域。

图3 盘车载荷分布图
在下胎封固过程中,主要的目标有2点:1)结构在摆放和运输过程中的稳定性与安全性;2)减小分段在摆放和运输过程中的变形。因此,下胎封固工艺的一般原则如下:
1)2个托架对称于重心分布,摆放方向视分段长宽而定。
2)托架尽量摆放在强力连续结构的正下方。
3)支撑结构成对布置,每对槽钢或钢墩对称于分段重心与托架中心分布。
4)支撑位置尽量避开可能碰到的结构和开口等。
5)考虑稳定性的影响,支撑工具(托架、钢墩)不宜太过靠近分段重心。
2 分段下胎封固支撑点优化算法设计
本节建立了双层底分段模型的下胎封固方案数学优化模型,描述优化算法的实现过程,使用改进的随机行走法进行求解,得出优化的下胎封固支撑点方案。
2.1 下胎封固方案优化模型的建立
以直线代表分段横纵向的结构,纵向结构数量为a,横向结构数量为b,经过映射形成网格线。如图6所示,网格上的点即为横纵向结构交叉点,可以作为钢墩支撑点的备选位置。为了找到最优的支撑点方案,建立如下优化模型:
1)目标函数f(x)
以分段支撑之后的最大变形f(x)最小为目标函数,即下胎封固之后使分段的变形最小为优化目标。
2)设计变量x
设计变量x(i,j)为各支撑点的位置编号,不同的x对应不同的钢墩支撑方案;i代表支撑点所在的横向构件编号,j代表纵向构件编号。
3)约束条件
根据下胎封固的工艺原则,支撑结构不能靠近分段中心,因此托架上某个钢墩位置的可选方案如图4所示黑框内的n个点,优化算法可以就这个钢墩位置进行计算,其他3个钢墩根据重心对称原则确定,这样形成n种支撑方案,将n种支撑方案进行编号。根据不同方案下的分段最大变形量,从而得出最优支撑方案。因此约束条件为:1≤x≤n,x∈N*,N*为正整数;i、j的约束条件根据分段的横纵构件个数来确定,1≤i≤b,1≤j≤a。
综上所述,本研究中下胎封固问题的最优化模型如下:

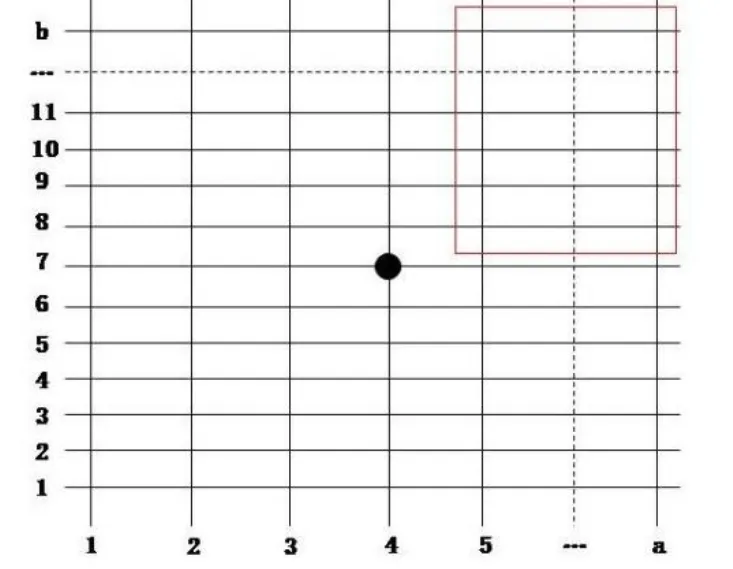
图4 分段结构映射网格图
2.2 应用随机行走法优化支撑点位置
随机行走法在给定初始点的前提下,在给定的以步长为半径的范围内,通过生成随机数的方式不断比较迭代,找到最优解。文献[5]给出的随机行走法可以用来解决全局最优化问题[5],随机行走法操作简单,不容易陷入局部最小值,将随机行走法进行改进,迭代过程中随机生成3个新的支撑位置而不是1个,可以进一步提高全局寻优的能力,对初始值的依赖也进一步降低。
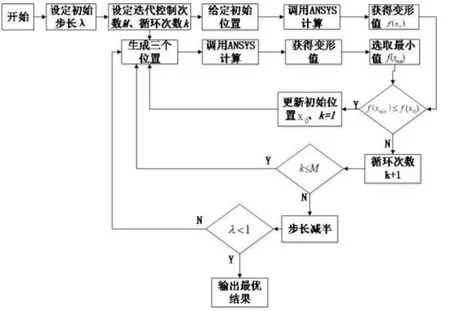
图5 支撑点优化计算流程图
在确立了优化模型之后,本文采用改进的随机行走法进行钢墩位置的自动优化,随机行走法适合这种组合优化问题,找出全局最优解;在实际计算时并不需要对每个可选方案都进行计算,而只需要对迭代过程中涉及的支撑点方案进行迭代寻优,大大减少了计算量。图5是支撑点优化计算的流程图,采用改进的随机行走法,初始迭代点x0行走寻优的过程如下:
1)程序开始,设置初次行走步长λ=3。
2)设置迭代控制次数M=3,并用变量k记录循环次数,k设初始值为1,k≤3。
3)给定钢墩的初始位置,将钢墩的初始支撑位置设在分段靠近中间的区域,这也符合下胎封固方案设计的实际情况,然后开始寻找更优的支撑点。
4)调用ANSYS计算初始位置的变形,读取分段结构的最大变形值δmax,并传递回MATLAB优化控制算法程序中作为目标函数值,即令f(x0)=δmax。在调用ANSYS计算过程中,将各方案的计算结果保存,如果有重复计算的方案,直接从保存结果中获取。
5)在初始位置以步长λ为半径的范围内随机生成 3个新的支撑位置x1、x2、x3,即生成了新的 3组支撑方案,然后调用ANSTYS计算这3组支撑方案的最大变形量,即获得f(x1)、f(x2)、f(x3)的值。将f(x1)、f(x2)、f(x3)进行比较找到3组方案中的变形最小值,记为f(xmin),并将最小值的支撑点记为xmin。
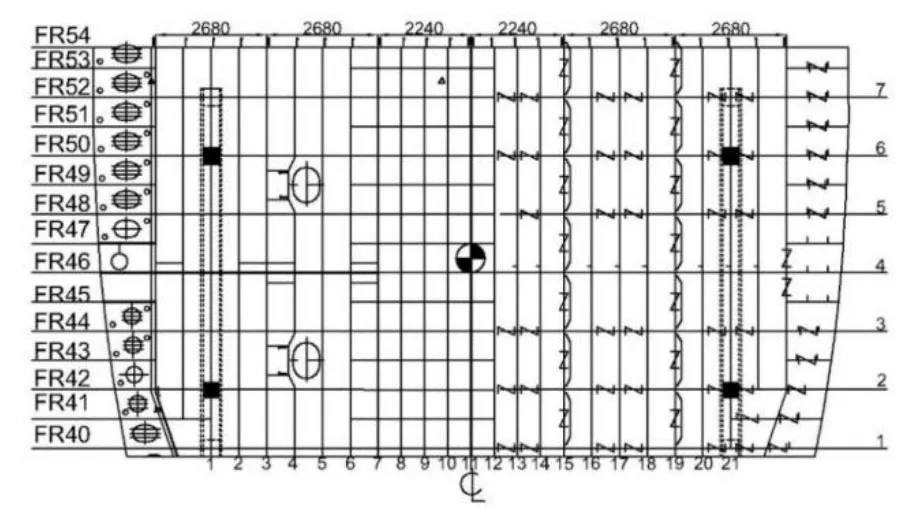
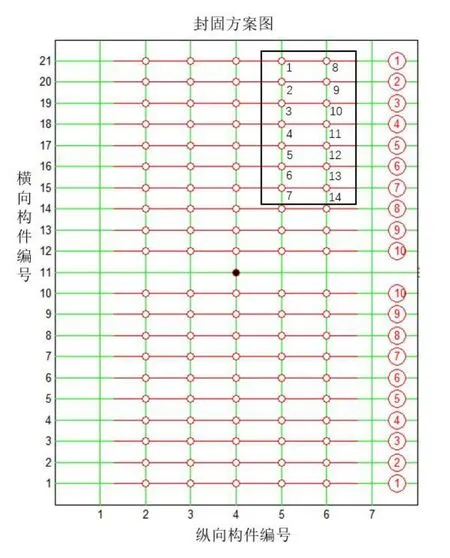
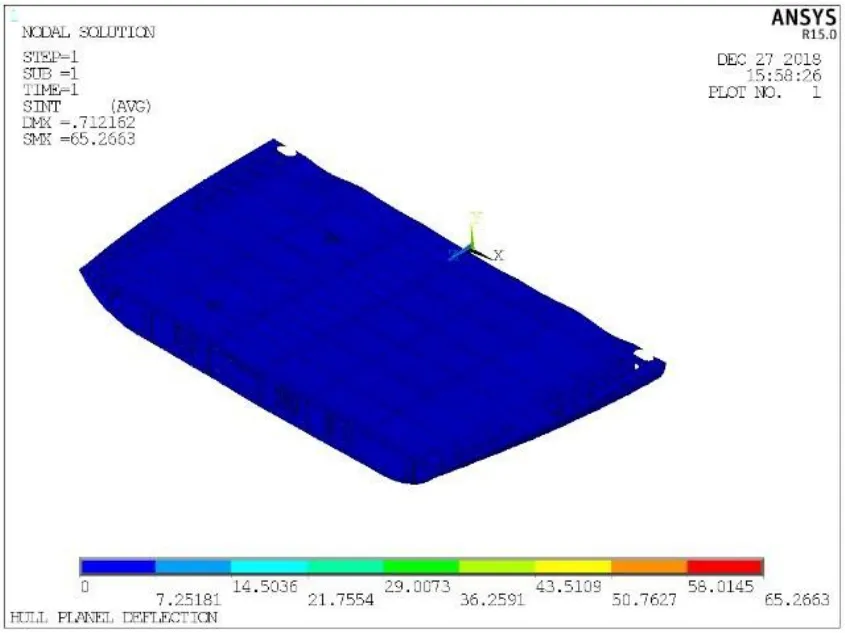
6)将f(xmin)与f(x0)进行比较,如果f(xmin) 7)判别循环次数k≤M,如果是Y,则返回5)处,继续迭代计算过程;如果是N,将寻优范围缩小一半,即把步长λ减半,返到5)处,再次以此步长为基础生成3个位置,开始新一轮行走。当步长λ<1时程序停止,此时输出最终的最优解xmin以及f(xmin),这就是最佳的钢墩支撑位置与变形量。 本节以某船102分段为例,分析其结构特点,结合下胎封固工艺原则,对某船型102双层底分段的下胎封固方案进行分析,并应用前文所述支撑点优化算法进行支撑点优化。 图6为某船102双层底分段的结构简图,该分段总重为68 t,其重心位于距中心线32 mm的左舷一侧,纵向位置为FR46+483 mm,垂向位置为内底面下方567 mm处,重心大致位于分段平面的几何中心。强力横向结构分别为FR40、FR42、FR44、FR46、FR48、FR50和FR52。其中FR46为舱壁,其余为带孔的连续肋板。长度方向,纵骨间距靠近中心线部分为560 mm,其余部位为670 mm。在中心线处及距离船中2 240 mm处有连续水密舱壁,在距离中心线4 920 mm和7 600 mm处有强力纵桁。 1)托架的可选方案 根据102分段的重量,选择2个40 t型号的托架。此型号托架高1 800 mm,长7 800 mm。托架的位置可以放置于纵桁和纵骨的正下方,左右舷各放置1个。分段最大宽度18 200 mm,长度为9 800 mm,托架沿长度方向放置,如图6所示。 2)支撑点可选方案 102分段为重心较低的平面分段,采用钢墩支撑的方案。每个托架上设2个钢墩,共计4个钢墩,对称分布于重心。根据此前的托架位置,钢墩的位置选在纵桁或纵骨与肋板的交叉点处。如图7所示,将肋板重新编号为 1-7,将纵骨或纵桁重新编号为1-21。除去4号肋板与8-15号纵桁,钢墩的位置可以选在其余肋板与纵桁或纵骨的交叉点处。根据对称原则将支撑点进行组合,一共可以得到14种方案。为了得到最合适的下胎封固方案,有必要进行优化计算。 图6 102分段结构简图 根据图6所示102分段结构,以直线代表分段横纵向的结构,经过映射形成网格线。如图7所示,网格上的点即为横纵向结构交叉点,可以作为钢墩支撑点的备选位置。 程序设置随机行走法的步长为 3,采用优化程序计算,其间调用ANSYS进行计算7次,得到9号钢墩位置方案最优,对应于左右舷距分段距中心线4 920 mm纵桁与FR42、FR52的交点,最大变形值为0.71 mm。 本文采用ANSYS软件建立102分段的有限元模型,如图7所示,坐标轴原点位于分段艏部中心线处。应用 SHELL63单元模拟分段中的钢板,BEAM188单元模拟纵骨,弹性模量设为2.06×1011Pa,泊松比为0.3,惯性载荷取为9.8 m/s2。 图7 102分段结构简化模型图 最优方案变形如图8和图9所示,变形最大处位于坐标原点的艏部开口位置,最大变形为0.71 mm,此变形量相对于整个分段来讲非常小,对分段结构的运输及合拢装配等不会产生影响。最大应力位于肋板开口处和支撑点处,最大应力为65.3 Mpa,整体分段没有大的应力集中区,且应力水平较低,结构不会发生屈曲变形。 本文采用随机行走法对某双层底分段的下胎封固方案进行优化,计算结果较好。为了适应不同分段进行下胎封固方案的计算要求,应用 MATLAB软件开发了分段下胎封固方案优化的计算程序,相关的功能模块都集成到程序GUI界面中。图10为下胎封固方案选择界面,将分段信息输入对应的文本框,点击对应按钮,右上方则输出对应的工艺要求,左侧的封固方案图显示托架和钢墩的推荐方案。在优化完成之后,界面会弹出提示框。点击查看结果,可以进入下胎封固方案结果显示界面,如图11所示。可以在右上方显示各个支撑点的坐标,并显示优化方案的分段结构最大变形值,在界面左侧显示分段变形、应力等云图。 图8 102分段最优方案垂向变形云图 图9 102分段最优方案应力云图 图10 下胎封固方案选择界面 图11 下胎封固方案结果显示界面 本文基于船厂下胎封固工艺的一般原则,以结构变形量最小为优化目标,采用随机行走法对封固支撑点进行了优化,并以某船102分段为例,设计了分段的下胎封固可选方案,包括托架的方案和支撑点的优选方案,优化结果表明基于随机行走法的下胎封固支撑点优化算法是可行的。目前,本算法适用于一般的船体双层底分段,未来结合船厂Tribon软件所建立的分段模型,可以开发各种分段下胎封固方案计算的程序,为船厂提供下胎封固工艺优选方案。3 某船102分段下胎封固方案的分析
3.1 某船102分段介绍与分析
3.2 下胎封固过程中支撑工具的可选方案
3.3 支撑点优化及结果分析
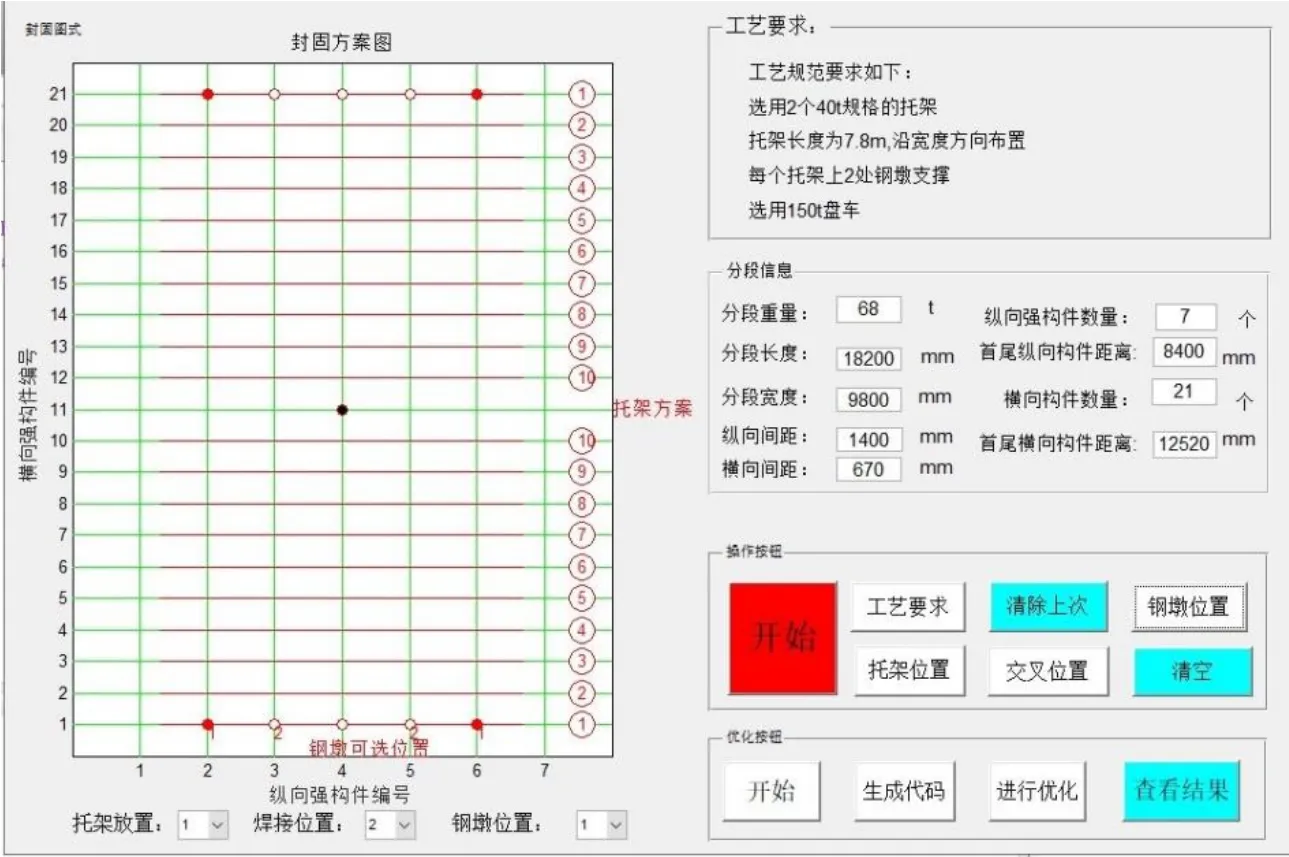
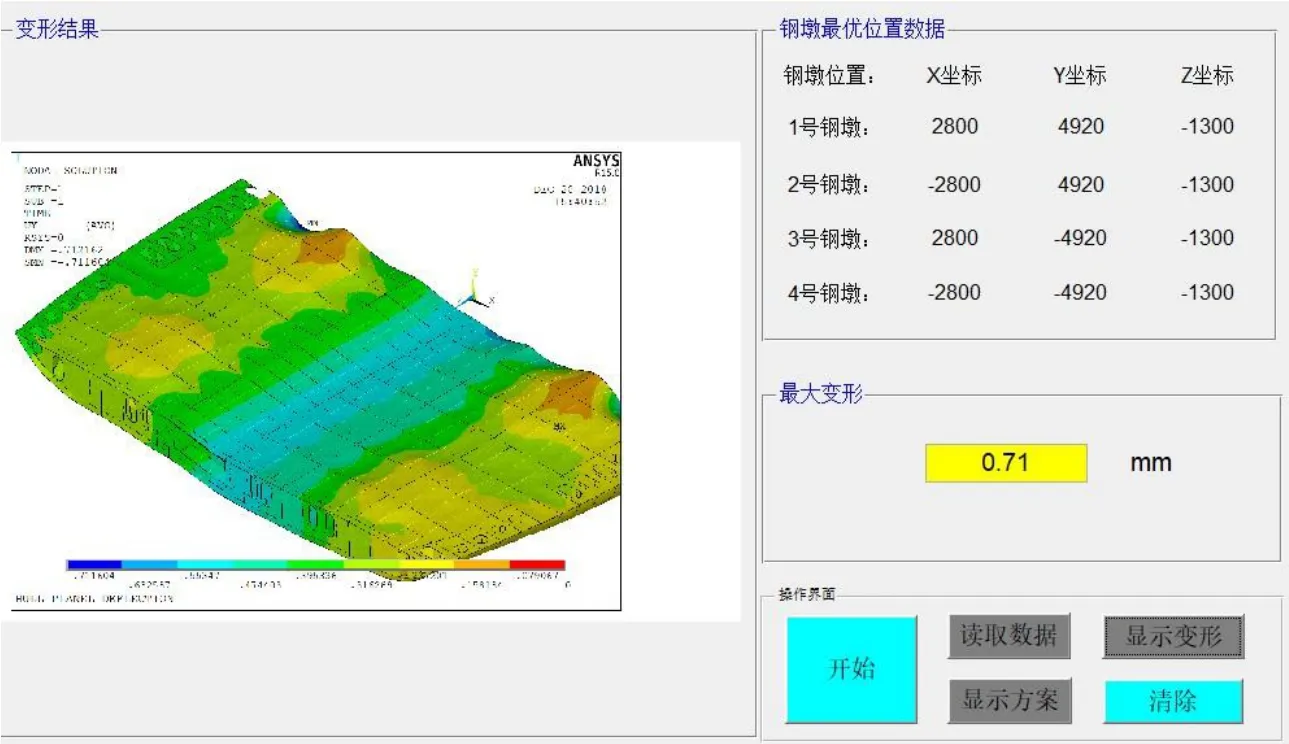
3.4 优化程序可视化界面开发

4 结论
