导数中的最值问题
2020-06-13任素巧赵百利
高中数理化 2020年2期
任素巧 赵百利
利用导数法确定函数的最值问题往往需要通过求解相应的函数在对应区间上的单调性,进而确定其极大值或极小值,再比较极值和端点处的函数值的大小,有时还要结合具体问题进行分析.本文结合实例对利用导数法破解最值问题的一些常见题型加以剖析.
1 最值的求解问题
最值的求解问题往往包括在确定区间求函数的最值和在含参区间求函数的最值等.


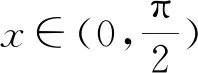

2 参数的确定问题
此类问题需要利用逆向思维,比较极值和端点处的函数值的大小,从而来确定相应的参数的值或取值范围.


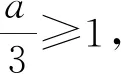

综上所述,当且仅当a=0,b=-1或a=4,b=1时,f(x)在[0,1]的最小值为-1,最大值为1.

3 创新的应用问题
导数作为一种最值的求解工具,经常利用导数法来解决一些创新的应用问题,达到巧妙应用的目的.



