例谈高考三角函数及解三角形问题的备考建议

胡能其

三角函数及解三角形是高中数学的主干知识,也是高考的必考内容.本文通过对近三年全国卷Ⅰ文科和理科试卷进行考点分析,归纳出常考知识点,并以高考真题为例总结每个考点的解题方法.

1 考点分析

1.1 2017—2019年高考全国卷Ⅰ考点分布

为了更清晰地归纳高考三角函数的考点,笔者整理了数学全国卷Ⅰ近三年的试题,得出表1.

表1 全国卷Ⅰ近三年考点分布表

1.2 题型与分值

由表1不难发现,2017—2019年全国卷Ⅰ理科考查的题型均为一道小题和一道大题,大约17分,题型、分值相对稳定;而文科考查的题型都是小题,但不管是分数值还是难度都有不同程度的提升.

1.3 主要考查内容

纵观近三年全国卷Ⅰ文科和理科的主要考查内容，包括三角函数定义、三角恒等变换、三角函数图象与性质、解三角形等.

2 典例剖析

2.1 任意角三角函数的定义

任意角的三角函数定义在高考中单独命题虽然不是热点,但也偶有考查,所以也要引起重视.

分析先由正切函数定义,得到a,b的关系式b=2a,再利用二倍角公式以及余弦函数的定义求得a的值,进而求得|a-b|的值.

2.2 三角函数的恒等变换

三角函数的恒等变换是历年高考的一个必考点,主要考查三角函数的求值和化简,考查学生对三角函数公式的正用、逆用及变形运用,难度中等.

1) 三角函数的求值问题

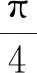
2) 三角函数式的化简

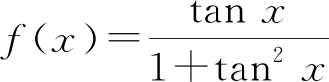
2.3 三角函数的图象与性质

三角函数的图象与性质是高考的热点,经常以选择题、填空题的形式出现,对考生综合能力要求较高.

1) 三角函数的图象变换

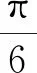
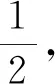
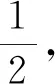
分析先利用诱导公式将函数“同名”化,然后利用图象平移、伸缩变换分析即可.

2) 三角函数的性质

三角函数的性质主要包括三角函数的单调性、周期性、对称性、最值等.解决三角函数性质问题主要是利用数形结合的思想、化归思想和换元法进行求解.

A.f(x)的一个周期为-2π

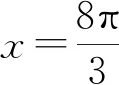
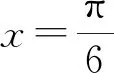
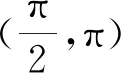
分析先求得f(x)的相关性质,然后再逐一检验,选出正确答案.

3) 三角函数的最值

三角函数最值问题主要有三种,一种是将三角函数转化为y=Asin (ωx+φ)+h的形式,然后利用三角函数本身的有界性得出最值；一种是将三角函数最值问题转化为求一元二次函数的最值；另外一种是利用导数研究最值.

A. 4 B. 5 C. 6 D. 7

分析先利用余弦函数二倍角公式和诱导公式,将函数转化为以“sinx”为自变量的一元二次函数,然后利用一元二次函数求最值的方法求解.

2.4 解三角形

解三角形知识除了应用正弦定理、余弦定理以及面积公式外,往往还要结合三角函数相关公式.

(1)求A;

分析第(1)问先利用正弦定理将角的关系转化为边的关系,再用余弦定理求得角A的值;第(2)问则是先利用正弦定理将边的关系转化为角的关系,再利用三角恒等变换求得结果.