变结构时态神经网络模型在股票预测中的应用
2020-06-12孟志青朱涵琪
孟志青,朱涵琪
(浙江工业大学 管理学院,浙江 杭州 310023)
0 引 言
现实生活中存在大量非平稳时序数据,用传统的预测模型很难进行准确的预测,例如股票价格时间序列受复杂因素的影响,具有非线性和非平稳性,很难预测股票价格变化。目前国内外学者对股票时间序列提出了许多预测模型,其中典型方法有GARCH-M模型[1]、神经网络模型[2,3]、SVM[4]等。此外,在对数据进行前期处理上,主要的方法集中在对研究变量本身以及相关变量的分析上。文献[5]通过对输入变量进行主成分分析,避免了变量过多、网络结构复杂的问题。文献[6]用粗糙集理论降低了股票价格趋势的特征维数,简化了预测模型。文献[7]、文献[8]、文献[9]运用小波分析方法,对时间序列在预测前进行处理,将时间序列分为低频和高频序列。当数据呈现非线性和非平稳性时,单一的预测模型很难发现含有时间的规律变化。例如股票市场数据包含时间属性,几乎无法发现随时间变化且在不同状态上相互联系。另外,周期的选择是股票市场预测的重要依据。特别是用小波分析与神经网络结合预测时[8,9],经小波变换进行伸缩和平移运算而产生的各频率序列与原始数据相比发生了一定的变化,继续采用固定的经验分析周期和单一神经网络结构进行预测已不再适用。时态数据挖掘是通过数据在时间上的重新划分发现非线性与非平稳数据的内在规律[10,11],例如近似周期、近似关联规则等。采用不同的时间粒度或时态型对数据进行分析时,会呈现出不一样的变化规律。为了克服非线性和非平稳数据难以发现有规律的知识,以及盲目选择经验周期带来的不必要误差,本文设计了一种变结构时态神经网络预测模型用于解决股票价格的预测问题。
1 数据预处理
在对股票时间进行预处理上,采用小波变换的方法,通过伸缩和平移等运算,对信号进行多尺度分析,可以由低频到高频逐步地观察信号。小波分析理论与神经网络结合,可加强对高频序列适应能力,提高预测精确度。
一般小波变换可以分为连续小波变换和离散小波变换[12]。连续小波变换表示为:
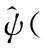

本文通过采用以多分辨率分析为基础的Mallat算法,实现离散小波变换。基本思想是设Hjf为能量有限信号在分辨率2j下的近似,则Hjf可以进一步分解为在分辨率2j-1下的近似Hj-1f以及位于分辨率2j-1和2j之间的细节之和。将原始的时间序列被分为低频部分和高频部分,然后只对低频部分进一步分解,直到达到预设的分解层数。
2 时态数据转化表示
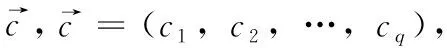
在现实世界中,我们可以将时间与实数轴联系起来,从而将实数轴上的点代表某一时刻,并对应着点所在的实数,称为绝对时刻。下面引入时态型定义。
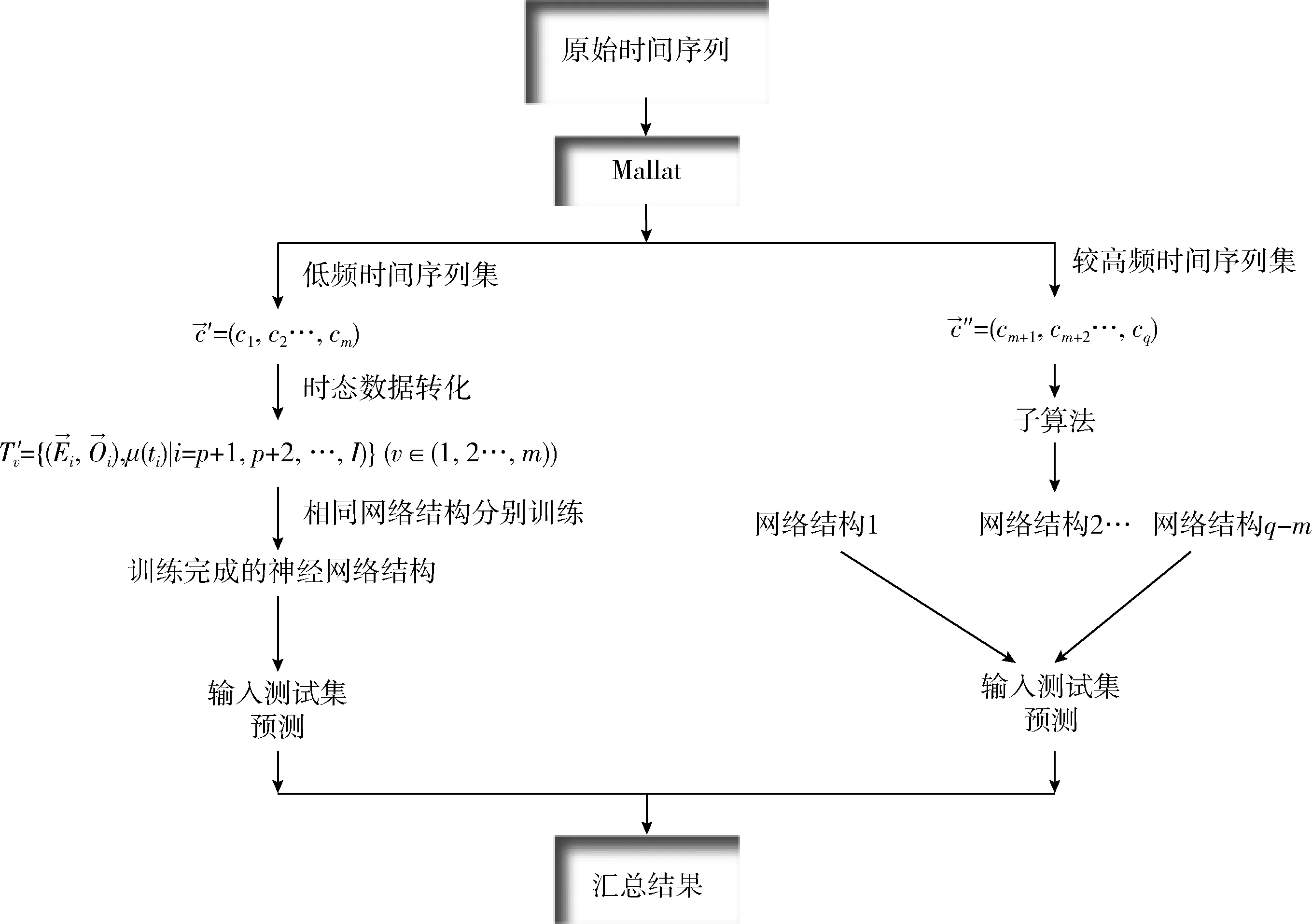
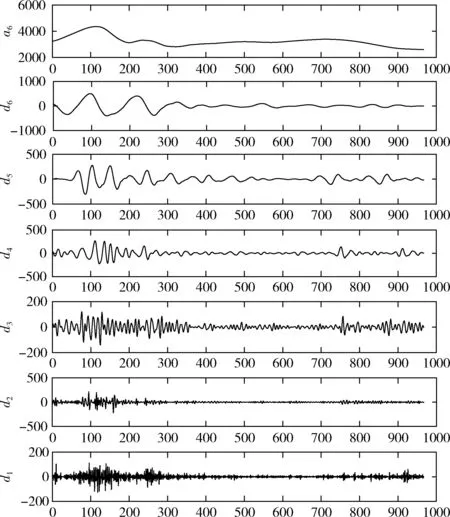
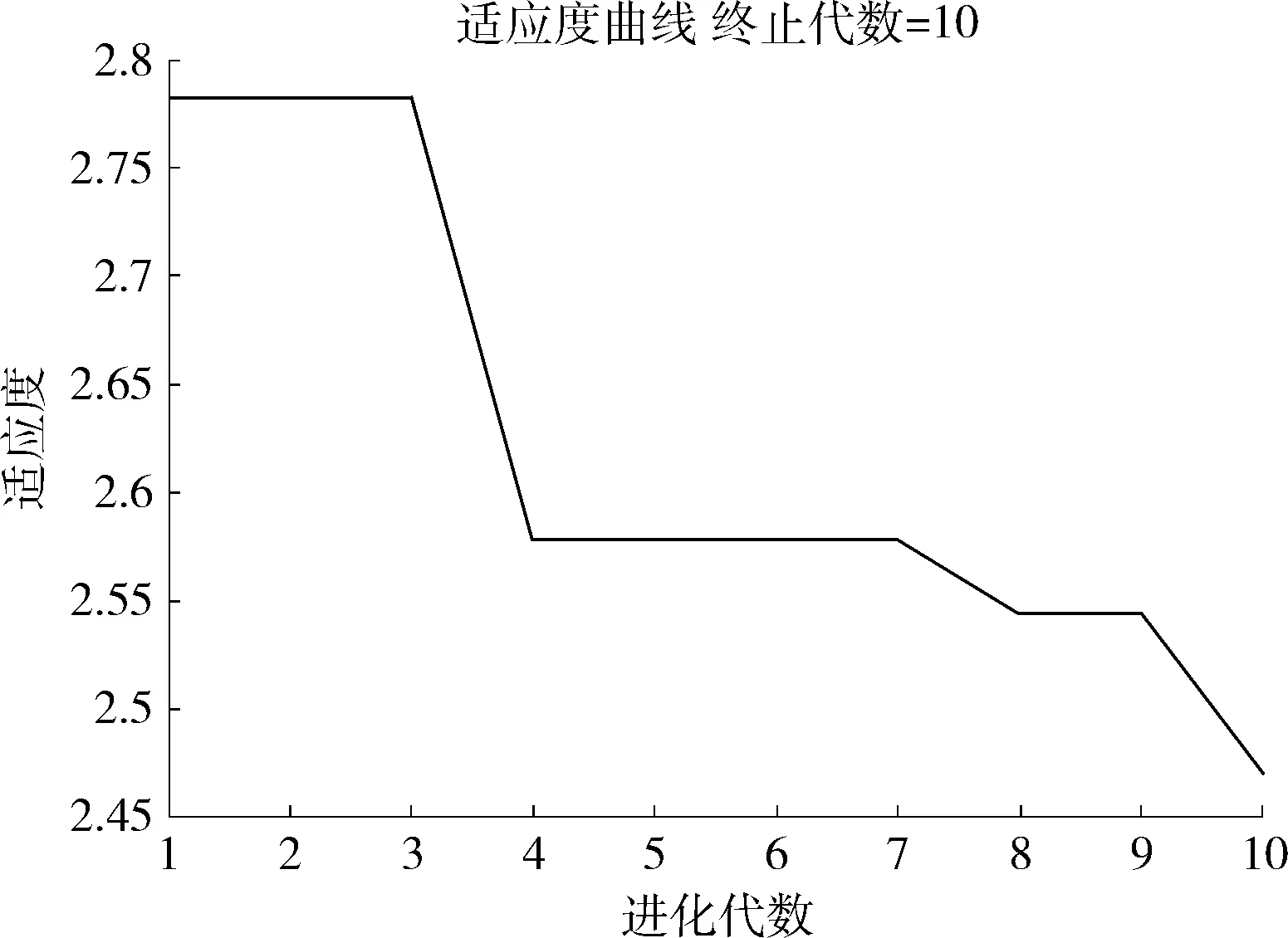
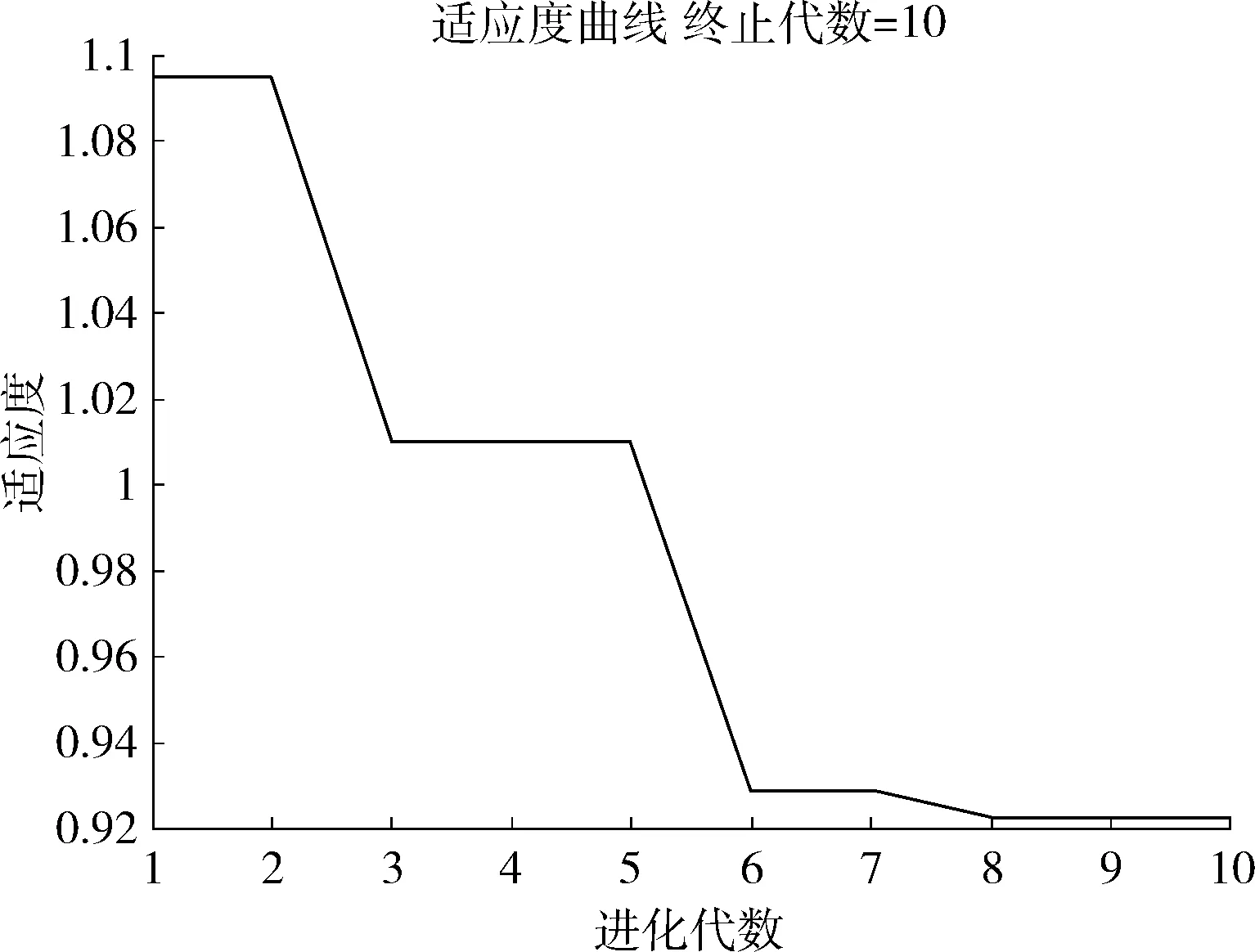
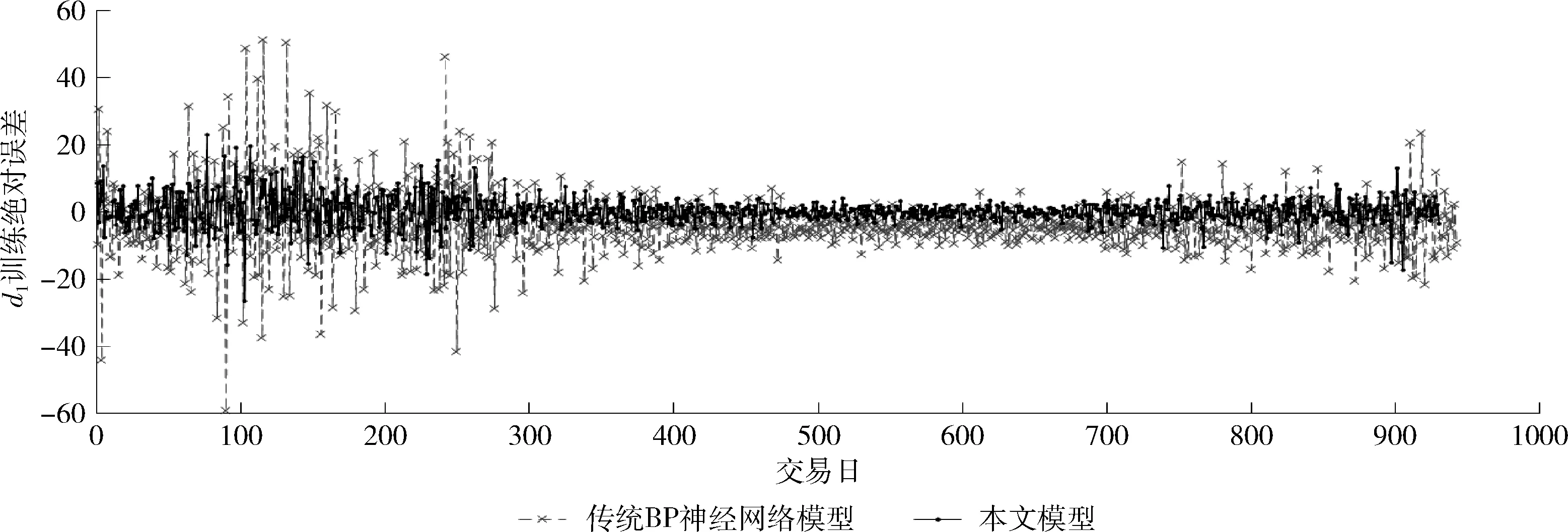
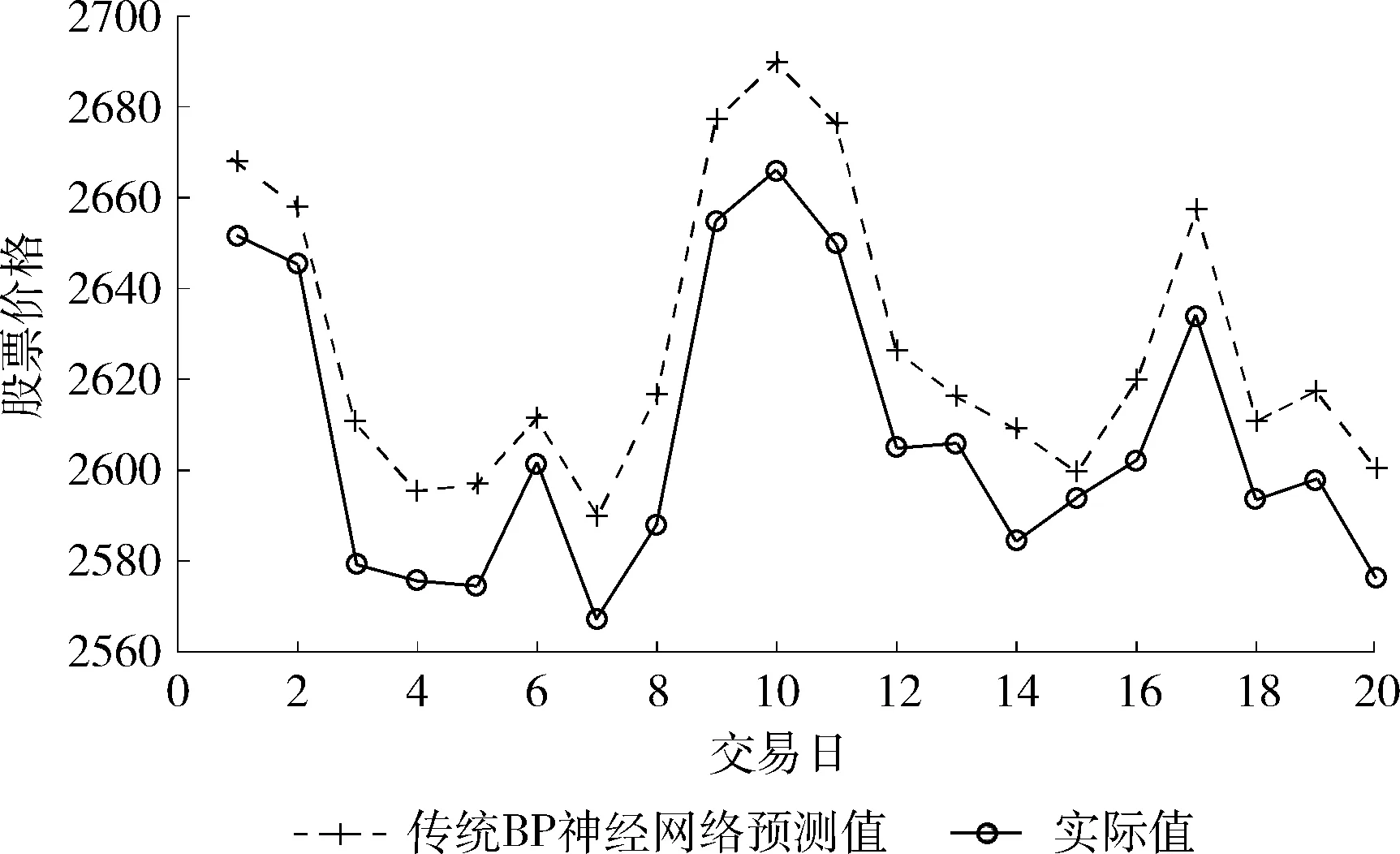
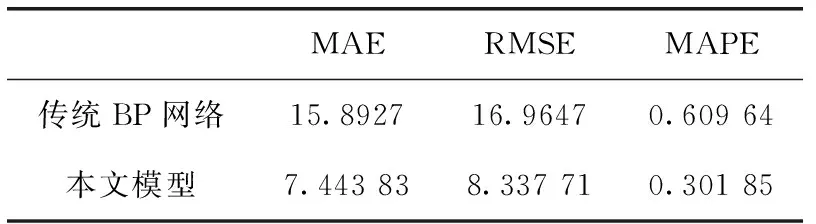
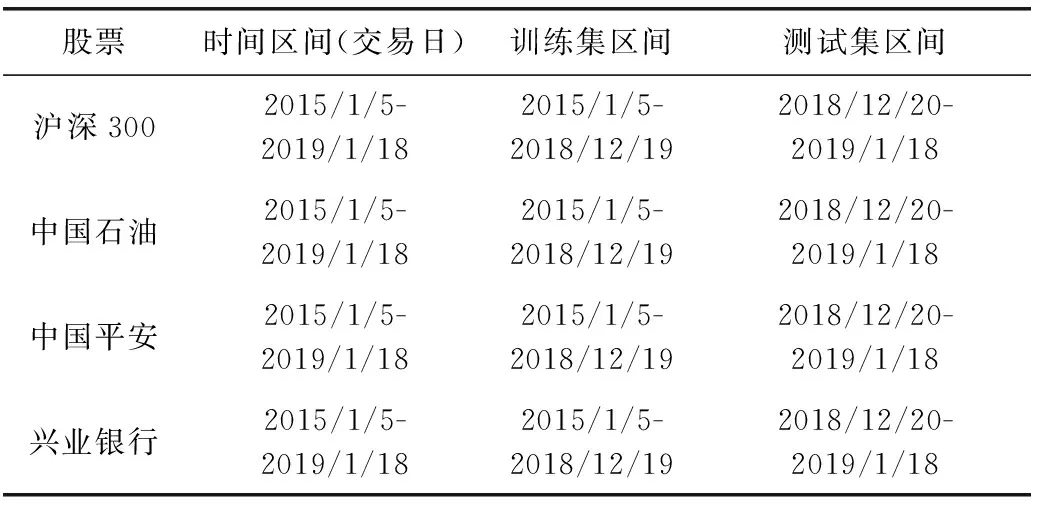
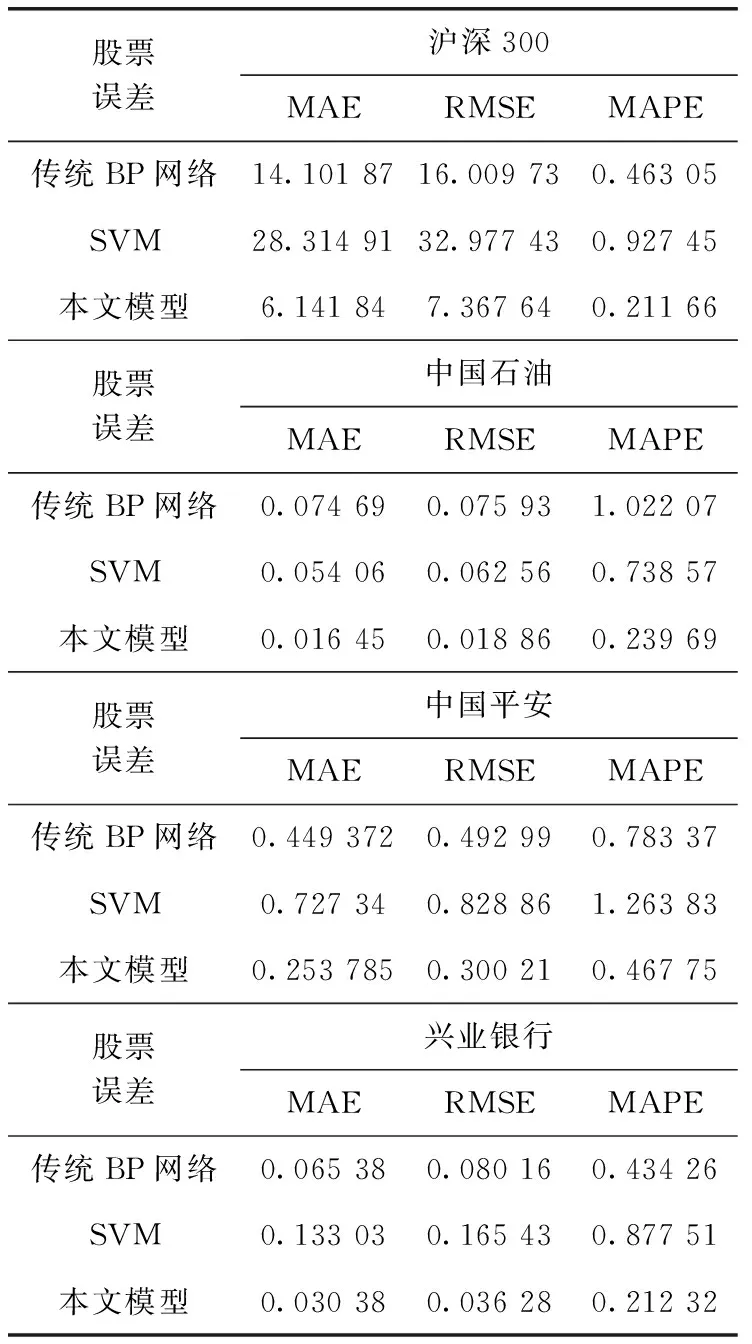
定义1[10]设μ是从绝对时刻t到绝对时间的映射,即R→2R如果μ满足下列性质:①(非空性)t∈μ(t);②(单调性) 若t1 则称μ为时态型,μ(t)为μ的时态因子。由此可见时态型μ是对时间轴的一个划分,每个时态因子是一个绝对时刻的集合。时态粒度、时态序等相关具体知识参见文献[10]。 神经网络有多种结构类型、灵活的学习算法和验证过程,在建模过程中不需要做一定的经济假设,它们可以独立学习变量中固有的关系,这在证券投资和其它金融领域十分有用。本文采用的是根据时态模型改进后的基于误差逆传播BP算法的前馈神经网络。 设神经网络输入层p个节点数(j=1,2,…,p)和隐层L个节点数(l=1,2,…,L),输出层M个节点数(k=1,2,…,M)。 初始化输入层、隐层和输出层神经元之间的权值γjl,γlk,隐含层阈值α(α=(α1,…,αl,…,αL)),输出层阈值β(β=(β1,…,βk,…,βM)),学习率η,神经网络训练过程如下。 步骤1 信号的向前传播过程: 步骤2 信号的向前传播过程: 由于节点数需要是整数,而PSO算法是一种处理连续变量的群体寻优算法,在连续型PSO算法的位置更新过程中不能产生整数变量。因此,在初始化位置和更新位置的过程中需要对其进行四舍五入,将得到的实数取到最近的整数。具体过程如下: 首先初始化粒子群:假设在一个D维的搜索空间中,种群有n个粒子:X=(X1,X2,…Xn),其中第i个粒子表示为一个D维向量:Xi=(xi1,…,xid,…xiD),代表着第i个粒子在D维搜索空间中的位置。 xid=popmin+round(rd(popmax-popmin)), [popmin,popmax]为xid的整数范围,round(·)表示四舍五入,rd表示(0,1)之间的随机数;初始化第i个粒子的速度:Vi=(vi1,…,vid,…,viD),vid的范围为[vmin,vmax]。 输入:某一高频序列: 时态型μ PSO算法种群数sizepop和迭代次数maxgen 分析周期最大值pmax, 最小值pmin 输出节点数M 过程: 步骤2 初始化新的神经网络,包括权值和阈值的初始 化、学习率η、训练函数和传递函数的选取。 步骤3 将时态数据T″v带入神经网络模型进行训练。 步骤4 通过上一步,得到在初始神经网络结构下的训练误差w,以此作为PSO寻优算法的初始适应度值。 步骤5 repeat: (1)更新粒子速度和位置:得到新的输入节点数p和隐层节点数L,p根据值将序列c″v转化为新的时态数据T″v。 (2)根据上一步得到的p值和L值,初始化新的神经网络包括权值和阈值初始化、学习率η、训练函数和传递函数的选取。 (3)将时态数据T″v带入上步确定的神经网络进行训练,计算误差w,得到新的粒子适应度值。 (4)根据上步得到的粒子适应度值更新个体极值和群体极值。 until 达到迭代次数 步骤6 得出最优个体适应度值对应的粒子位置Xbest=(xbest1,xbest2)。 输出:某一高频序列c″v的神经网络结构,其中:xbest1=p(输入节点数),xbest2=L(隐层节点数)。 总体来看,变结构神经网络时态数据预测模型实现过程如图1所示(主算法)。 图1 主算法流程 主算法的具体过程如下: 步骤2: (1)选定经验周期p、隐层节点数L,初始化神经网络,包括入节点数、隐层节点数、输出节点数、权值和阈值初始化、学习率η、训练函数和传递函数的选取。 (3)将时态数据T′v带入神经网络中进行训练。 end for 步骤3: 利用子算法,得到c″v对应的神经网络结构 end for 步骤2过程确定了较低频序列集训练完成的各神经网络模型,步骤3过程确定了较高频序列集训练完成的各神经网络模型。最后利用经训练集确定好的神经网络模型,输入转化后的时态数据测试集,将各频率序列对应的神经网络输出结果相加,得出最终预测值。 以上就是基于时态数据的变结构神经网络建立过程。与传统的BP网络不同点主要在两点,数据按时态因子进入网络学习,不同节点上采用不同时态数据学习,不同的输入节点数和对应的隐层节点数不相同。 为了对模型的预测精确度进行分析,选取以下参数作为预测模型的评价标准。 (1)平均绝对误差(mean absolute error) (2)均方根误差(root mean square error) (3)平均绝对相对误差(mean absolute percent error) 实验环境:计算机处理器:Intel(R) Core(TM) i5-7200uCPU、内存4 G、256 G固态硬盘、显示芯片:NVIDIA GeForce 940MX、64 G操作系统,实验软件MATLAB R2016a。 实验数据为:从同花顺采集的2015.01.05-2018.12.18期间上证指数每日的收盘价。采用单步滚动预测,用前N日的股票收盘价作为输入数据,第N+1天的股票的收盘价作为输出数据。2015.01.05-2018.11.20之间的交易日数据用来训练,对未来20天交易日的股票价格进行预测。 图2 原始序列小波分解与重构结果 为了验证本文模型的有效性,将本模型与各频率采用经验周期为5的传统BP神经网络模型进行对比。其中两种模型中对网络权值和阈值优化的方法保持一致:隐含层神经传递函数为tansig函数,输出层神经元的传递函数为purelin函数,训练函数采用动态自适应学习率的梯度下降BP算法。当目标最小误差小于0.01(用均方误差MSE表示)时停止训练。 实验过程中,时态型μ选为天,低频序列集的分析周期采用经验分析周期5天,对应的隐层节点数经实验比较确定为7。高频序列集中相关的参数为:种群粒子数目sizepop选为30,分析周期最小值pmin为5,最大值pmax为25,迭代次数maxgen经多次实验后选为10,从图3、图4和图5可以看出,当超过10代之后,适应度变化很小甚至不再改变,同时迭代次数越多,会增加不必要的运行时间和空间。 图3 d1序列参数寻优 经实验最终得到d1序列上参数寻优的结果,如图3所示。当迭代到第10代时,适应度值达到最小,其对应的最优粒子位置Xbest=(xbest1,xbest2)为Xbest=(17,11)。由于xbest1表示的是输入节点数,xbest2表示的是隐层节点数,那么得到d1序列上的分析周期选为17,隐层节点数选为11。 d2序列上参数寻优的结果,如图4所示。当迭代到第8代时,适应度值达到最小,其对应的最优粒子位置Xbest=(xbest1,xbest2)为Xbest=(20,6)。那么得到d2序列上的分析周期选为20,隐层节点数选为6。 图4 d2序列参数寻优 图5 d3序列参数寻优 d3序列上参数寻优的结果,如图5所示。当迭代到第7代时,适应度值达到最小,其对应的最优粒子位置Xbest=(xbest1,xbest2)为Xbest=(8,11)。那么得到d3序列上的分析周期选为8,隐层节点数选为11。 图6 d1序列训练误差 图7 d2序列训练误差 图8 d3序列训练误差 图9 变结构模型预测 进一步将两种模型进行最终误差分析,在MAE、MAPE和RMSE这3个指标上本文模型比传统模型均降低了50%-60%左右,比较结果见表1。 为了进一步验证本文模型的适用性和有效性,另外选取了沪深300、中国石油、中国平安和兴业银行这4只股票,具体数据选取见表2。 将本文提出的模型,同时与传统BP神经网络模型、SVM方法进行比较。各模型和误差分析结果见表3。从表3中可以看出,本文模型相比较于传统BP网络、SVM的预测误差有明显的降低,进一步说明了将股票数据转化为时态数据,建立变结构模型的有效性。 图10 传统BP神经网络预测 表1 误差分析比较 表2 实验股票数据 表3 4种股票预测结果 本文提出了一个变结构时态神经网络模型,用于解决非线性和非平稳数据预测问题。通过实验,使用上述模型对具有明显时间属性的股票价格进行预测,将股票数据转化为时态数据集,对神经网络进行改进,以及对经小波变换之后的各个分支序列建立变结构时态神经网络预测模型,可以有效地降低分支序列预测误差,从而降低整体预测误差,对股票类似的时间序列分析具有应用价值。对于解决类似的非线性与非平稳数据预测问题具有重要的意义。 此外股票市场信息是海量的,与股票价格相关的变量和技术指标有很多,本文采用的是单变量分析,进一步可以在本实验的基础上采用多变量进行综合分析以提高预测效果。3 变结构时态神经网络设计

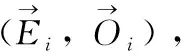
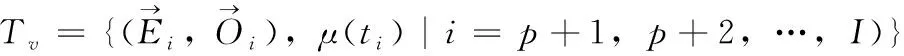
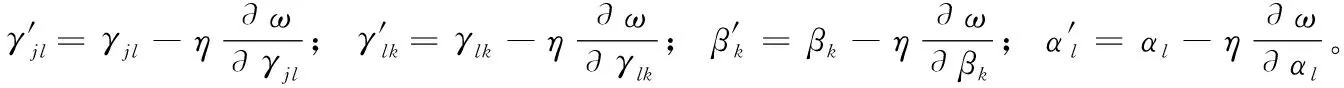
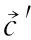

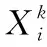
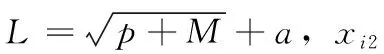

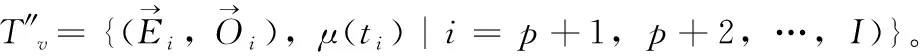
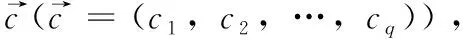
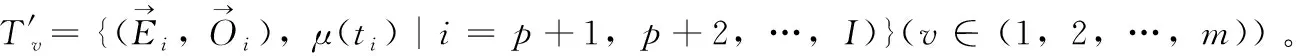
4 误差分析
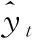
5 实 验
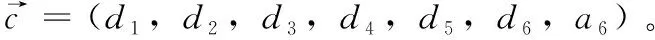
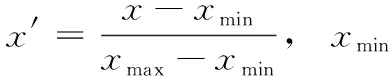



6 结束语
