基于节点测速的水下传感器时钟同步迭代算法
2020-06-12刘广钟田纪尧孔维全
刘广钟,田纪尧,孔维全
(上海海事大学 信息工程学院 水声传感器网络实验室,上海 201306)
0 引 言
节点间协调与合作完成各项分布式任务离不开时间同步技术作为支撑和依靠,它是多项关键性技术的基础[1],例如时分复用调度、传感数据融合、介质访问控制协议等等[2]。然而,水下传感器节点部署要求高,一旦部署完成很难进行维护和更换,所以传感器的计算资源与能量存储都十分有限。一些陆地传感器在进行时间同步时往往忽略传播延迟,然而在水下环境,巨大的传播延迟在节点通信时是不可忽略的重要因素,并且受到海水的温度、盐度、密度等多种环境因素的影响,水下声波的速度会发生随机性较大的变化。其次,传感器节点具有随洋流影响而移动的特点。当某节点发送消息和收到回复消息的间隔中,节点已发生了相对移动,导致传播延迟在每次信息交互中都会发生变化;更重要的是,水下传感器计算能力有限,不宜设计过于复杂的算法使其消耗大量能量。所以,在设计水声传感器网络的时间同步算法中,须考虑到上述特性。
本文综合考虑了水声通信中存在的各种特点,提出了一种水下传感器时间同步算法。本文主要贡献如下:
(1)考虑节点的移动性与空间相关性,通过一种节点运动速度估计公式,计算出待同步节点的移动速率,这是提高时间同步精度的重要因素。
(2)使用3个锚节点辅助待同步节点完成时间同步,锚节点随机分布在水下环境,具有标准时间。完成时间同步的普通节点有机会称为参考节点,完成对剩余待同步节点的同步工作。通过此迭代方法可加快整个网络的收敛时间,更适用于高密度环境。
(3)采用发送-接收的信息交互模式,完成时钟频偏与时钟相偏的估计,并对误差较大的节点实施相偏补偿。
1 相关工作
目前,针对陆地传感器的时间同步算法的研究成果已十分丰富,但是它们都没有考虑到海洋环境的特殊性,并且忽略传播延迟的存在。因此这类协议并不适用于水下传感器。关于水下传感器时间同步的研究在近年来开始兴起,并且取得了一些研究进展。在文献[3]中提出了一种成簇时间同步协议,簇首节点直接向水面浮标发出同步请求,但未考虑某些簇首所处位置过深的情况,导致传播距离过远,影响同步精度。在文献[4]中提出了一种多源时间同步算法MSTS,通过多跳传输方法进行同步,但每个中间节点处理数据包时都会产生一定时延,经过多跳累积造成更大的延迟。并且更多的文献并未考虑到这个问题。在文献[5]中提出了基于能量衰减的时间同步算法Ea-Sync,使用移动信标节点对所有节点进行时间同步。文献[6]曾提出使用多普勒原理完成时间同步,通过检测接收到的超声波频率变化来实现时间同步校正,但该方法计算复杂,且应用场景局限性较大。文献[7]提出了一种多普勒辅助水下传感器网络时间同步机制,但文中只研究发送方和接收方相向运动时的情况,然而真实情况中水下环境复杂,节点可能更倾向于无规则运动,所以需要考虑到节点各种运动模式。且该方法实现难度过高,且需要额外的硬件才能完成,不适用于实际情况。Mobi-sync[8]引入节点移动模型,并使用3个信标节点对一个节点进行同步,通过一组速度矢量描述一个节点的运动情况,但此算法过于繁琐,能耗较大,实现有一定困难。
2 速度预测方法
由于受到水中洋流、温度、潮汐等多种环境因素的影响,水下物体的运动速度在方向与数值上发生较大的变化。根据目前的研究结果表明,水下物体的运动并不是完全随机,会根据洋流或者潮汐呈现半周期性的运动特点,这对于预测节点的速度有着积极的影响,我们可以通过一个具体的洋流模型来预测节点在水平方向上的运动速度。根据流体运动学中的假设,水下物体的深度基本保持不变,只在水平方向上发生移动。文献[9]使用了一种权威的二维洋流模型,本文也将使用此洋流模型对锚节点的运动状态进行预测,如式(1)所示
(1)
其中,c用来控制洋流位移速率,B(t)用来控制曲线的宽度,ε用来控制整个洋流场的振幅,参数ω就是流场中洋流流过的频率。按经验取值A=1.2,c=0.12,ω=0.4,ε=0.3,k=2π/7.5。一般情况下仅考虑节点在x和y方向上的位移,不考虑竖直方向上的位移,所以节点在x和y方向上的运动速度如式(2)所示
(2)
对于每个普通节点来说,由于其通讯能力有限,它不能与表面浮标通信,且无法预测自身运动状态,但是利用节点的时空相关性,其移动速度的估算可以实现。假定某普通节点j想要获得自身的速度[vx(j),vy(j)],其中vx(j),vy(j)分别是在x轴与y轴分量上的速度。如果节点j能够获取其周围锚节点的速度,则其自身的速度可以按式(3)计算得到[10]
(3)
其中,m为邻近锚节点的数量,ζij为差值系数,可用式(4)计算得到
(4)
其中,rij为普通节点与锚节点之间的欧几里得距离。需要注意的是,若要使用此运动模型,必须首先获得锚节点的运动速度。
3 算法设计与实现
为了完成本文提出的同步算法,我们将使用如图1所示的水下节点部署场景。场景中共有3种类型的节点,分别为浮标、锚节点和普通节点。浮标均匀部署在监测区域的水平面上,其能量充足,且带有GPS定位功能,具有全球标准时间。锚节点随机部署在水下区域,能与浮标直接通信,同样具有标准时间,用于辅助完成对普通节点的时钟同步。普通节点为待同步节点,其通信能力较差,无法与浮标直接通信,通过接收锚节点提供的信息完成自身的同步。本文将主要精力集中在处理锚节点和普通节点同步的问题上。
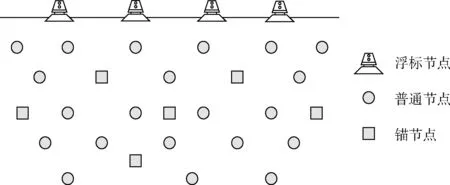
图1 监测区域网络拓扑结构
3.1 节点迭代同步方法
本文将在节点的同步过程中使用迭代递归法的思想。此方法可有效地提高整个网络同步的收敛速度,有效避免隐藏节点的问题,并适用于大规模的监测环境。其基本思想是已完成同步的普通节点也可充当锚节点的工作职责,继续对水中剩余的待同步节点进行同步。如图2所示,在网络初始化阶段,水中只有锚节点,通过不断广播数据分组告诉其它节点自己的身份和位置,此时所有普通节点皆未同步。其中普通节点A可通过接收在它通信范围内的3个锚节点1、2、3完成同步。已完成同步的节点A此时可扮演参考节点的角色,向网络中广播同步信息,普通节点B此时就可利用节点4、5、A完成同步,并以此不断迭代,直至所有节点完成同步。使用此方法的原因在于,水中锚节点的数量毕竟有限,会有一部分普通节点并不在锚节点的通信范围之内,导致这些节点无法进行时间同步。采用迭代法后将不会再存在上述问题,我们只需要保证每个节点都能接收到其相邻3个节点的信息即可。

图2 节点迭代同步过程
锚节点广播的数据分组结构见表1。

表1 锚节点广播数据帧格式
其中节点ID为每个锚节点的唯一标识号;时间戳我们选用MAC层获取的时间,用于表明信息的发送时间;速度向量为锚节点使用洋流模型预测得到的值;所有锚节点的置信度值皆为1,是普通节点识别锚节点的方法。
我们会考虑给每个锚节点和参考节点都设置一个置信度,每个待同步节点内部都会维护一张参考节点表,选取其中3个置信度最高的节点帮助自身完成时间同步。规定所有锚节点的置信度都为1。参考节点的置信度会按式(5)进行计算
(5)
其中,(u,v,w)是已完成同步的节点的位置,(xi,yi,zi)为辅助其完成时间同步的3个参考节点的位置。
本算法将会设置一个定位周期T,所有待同步节点都会周期性的更新自己的参考节点表,其中更新过程分为如下3个步骤:
(1)设置一个阈值,若某个参考节点广播信息的最后达到时间加上此阈值后仍未被收到,则认为此参考节点失效,将其从列表中移除。
(2)更新表中参考节点的位置。由于节点具有移动性,必须频繁获取锚节点的最新位置以提高算法的精度。我们将按式(6)完成更新
Local(i)=Local(i-1)+T×v(i)
(6)
其中,v(i)是在第i个周期中的估计速度。
(3)若接收到新的参考节点的广播消息,则将其信息和置信度添加到表中。
3.2 信息交换过程
本节的主要内容是描述锚节点与普通节点时间同步的具体信息交互过程,当普通节点的信息表中有足够的可用于同步的参考节点后,分别向各个节点发送数据分组请求开始时间同步进程,参考节点收到后,随即向普通节点发送多个包含同步数据的数据分组。具体的信息交互可如图3所示。

图3 报文交互过程
根据时钟同步原理,待同步节点A的本地时钟与标准时钟的关系为T=at+b,其中t是标准时间,a代表时钟频偏,b代表时钟相偏。A在T1时刻向锚节点发起同步进程,M在T2时刻收到消息后随即向待同步节点A发送多个数据分组,其时间戳用t[i]表示,A接收到信息的时间戳用T[i]表示。当节点M首次发送同步信息,其发送时间为t[1],经过时间d1后,信息到达待同步节点A,节点P记录下信息到达的本地时间T[1]。经过固定时间间隔后,浮标A再次向节点P发送第二个同步信息,由于节点受到洋流等影响会发生移动,在传播过程中不可忽略,信息传播延迟已不是t1而是t2。则可以得到
(7)
需要注意的是,M和A都具有移动性,则假设锚节点M的移动速度为VMi,待同步节点A的移动速度为VAi,水声传播速度为u,则可推出下式
udi=udi-1+VMi(di-1+di)+VAi(di-1+di)
(8)
此式的意义为,两节点在第i次交互时的距离等于第i-1次交互时的距离加上簇首与待同步节点在传播过程中分别发生移动而产生的距离。整理后可得
(9)
其中,VMi和VAi皆可由第二节提出的速度估计公式计算得出。得到传播延迟后,则时钟频偏可通过下式计算
(10)
3.3 误差补偿
在执行迭代算法的过程中,可以注意到,某些节点可通过3个锚节点辅助完成同步,但有部分节点可能以两个锚节点加一个参考节点的方式完成同步,最坏情况下,会有少数节点利用3个参考节点完成同步。这在一定程度上会产生节点定位精度不均的情况,利用3个锚节点的,定位精度一定最高,利用3个参考节点的,定位精度一定最低。对于这种情况,本文设计了一种校正方法,令所有未使用3个锚节点进行同步的节点获得相位偏差的补偿。我们通过设置一个时间置信度值(TCL)来区分不同情况下的节点,当一个节点是通过k(k=0,1,2)个锚节点完成时间同步时,规定其相应的时间置信度为TCL=k/3,TCL值越低,说明需要更多次数的时间补偿。
我们将采用发送-接收的交互方式使节点与锚节点在此进行信息交换。若在第一次同步时利用了两个锚节点,则在补偿时随机选择其中一个锚节点完成交互;若在第一次同步时利用了一个锚节点,则使用那唯一一个锚节点完成交互;若在第一次同步时未利用到锚节点,则选择一个置信度最高的参考节点进行补偿。
如图4所示收集4个时间戳Ta、Tb、Tc、Td,并利用下述公式完成时钟相偏的计算
(11)
t2-t1=aTd+aTa+2b-Tb-Tc
(12)

图4 信息交互方式
(13)
(14)
4 实验仿真
4.1 仿真参数设置
本文采用MATLAB进行仿真,并在相同环境下,比较本文算法与一些现有算法之间的性能差异。本文的仿真在1000 m*1000 m的水下环境内进行,其中共有200个传感器节点且为随机分布,节点运动采用随机洋流模型,并假设节点深度保持不变。仿真中使用的时间戳为MAC层时间戳。其它实验参数如下所示:
(1)时钟初始频偏(skew):40 ppm。
(2)时钟初始相偏(offset):80 μs。
(3)时间粒度:1 μs。
(4)传感器在水下的深度:100 m-1000 m。
(5)数据分组的间隔时间:1 s。
(6)接收端抖动:15 μs。
(7)节点移动速度变化:1 m/s-4.5 m/s。
4.2 实验结果及分析
由于网络中存在极少数节点无法与任何锚节点进行通信,为了将这种情况的可能性降到最低,我们将通过仿真确定最合适的锚节点数量比例。定义节点密度为节点邻域中的期望节点数,通过改变节点的通信半径来实现。节点覆盖度为通信范围内包含锚节点的普通节点的数量占节点总数的比例。图5显示了锚节点比例分别为5%、10%、20%情况下的节点覆盖度,随着节点密度的增加,覆盖度也随之提高,所以本文最后决定使用20%的比例设置锚节点的数量。
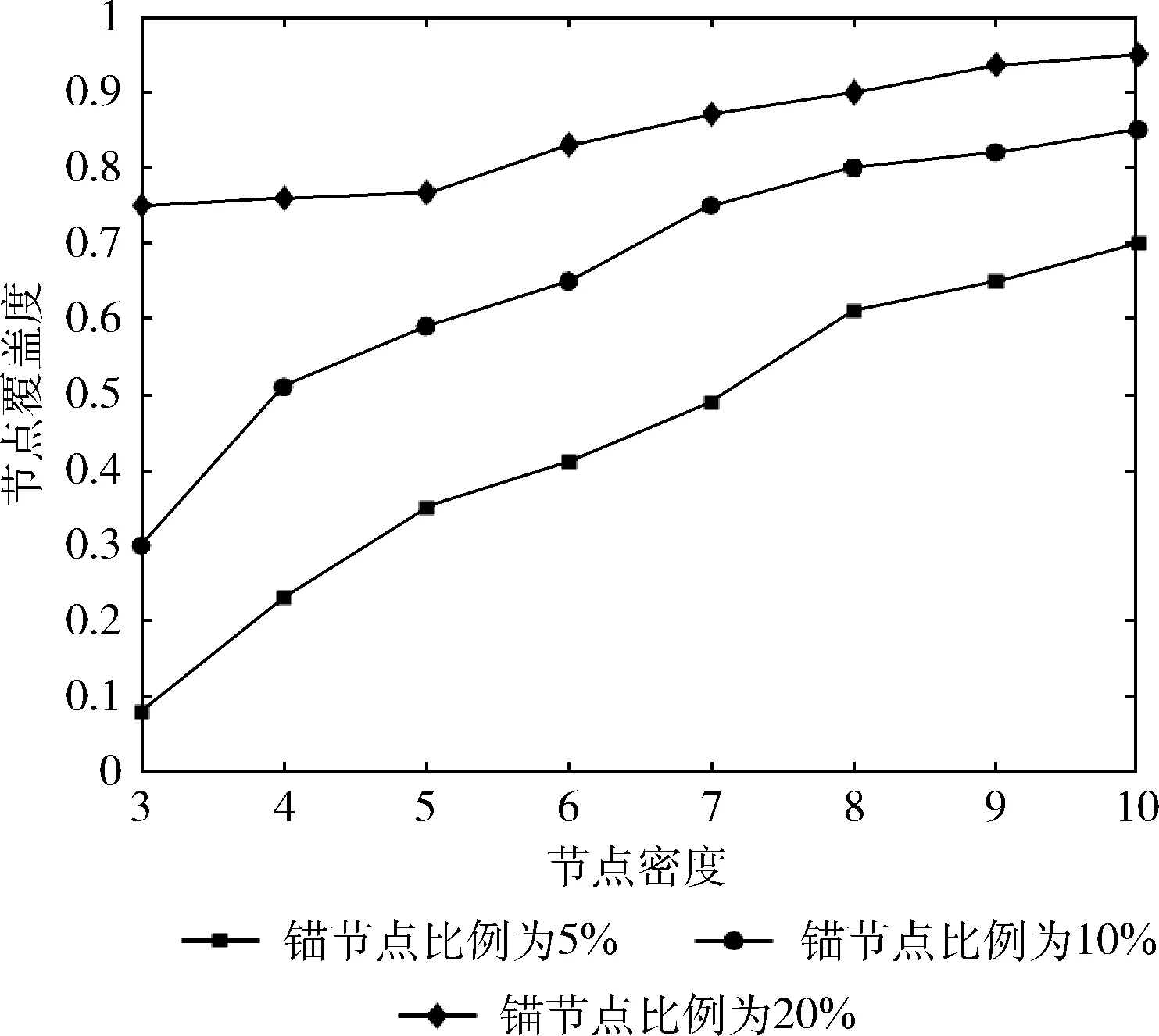
图5 锚节点比例与节点覆盖度关系
水下环境未知多变,需充分考虑算法在不同水域条件下的稳定性,图6显示了洋流模型中参数的变化对同步精度的影响,我们设置洋流流过的频率ω的变化区间为0.4-0.8,观察时钟频偏随ω的变化情况(图中括号后的数表示参与定位的锚节点的数量)。从仿真可以看出,误差会随着水流频率的增大而增大,使用3个锚节点进行定位的节点的误差趋于平稳,其它3种情况的误差都有不同程度的上升,由此可见对精度进行补偿的重要性。
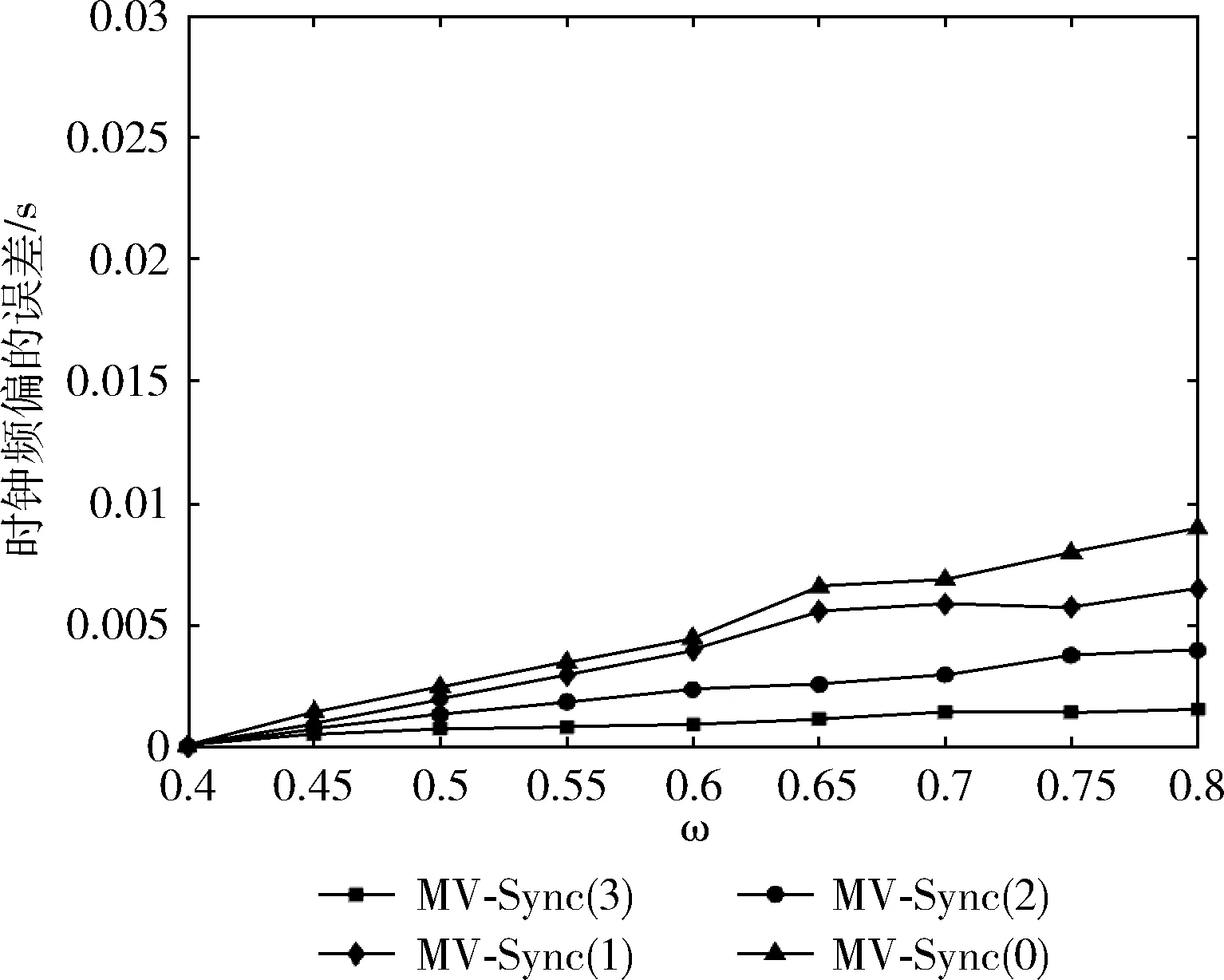
图6 洋流频率对时钟频偏的影响
图7展示了在整个系统完成时间同步后,本地时钟误差的增长趋势,通过将本文算法(MV-Sync)和TSHL、MU-Sync、NU-Sync[11]算法进行对比,从图7中可以看出,本文算法的误差累计明显小于其它算法,而且随着时间的推移,这种误差会成倍的增加,本文算法同步误差之所以会小于其它算法,一是因为通过多个节点辅助同一个节点的思想,极大程度上提高了同步精度;二是采用了洋流模型用于测算节点的速度,提高了传播延迟的计算精度。
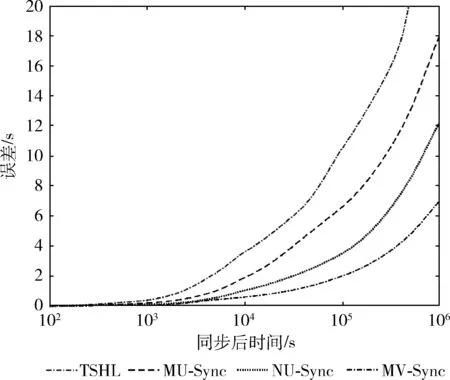
图7 时钟同步后时钟偏差的变化
传播延迟的动态变化主要是由节点的移动速度导致。图8分析了节点的移动速度对同步误差的影响,速度的变化范围从1 m/s-4.5 m/s,将本文算法与同样考虑节点移动性的MU-Sync、D-Sync、NU-Sync算法进行对比,从图中可以看出,四者的同步精度基本不受速度变化的影响,但是同步误差却有好坏之分,MU-Sync的误差主要在0.023 s左右,D-Sync的误差主要在0.013 s左右,NU-Sync的误差主要在0.006 s左右,而本文协议小于上述3种协议。

图8 节点移动速度对同步的影响
5 结束语
水下传感器的时间同步工作会受到节点移动、传播时延高、低能耗等因素的影响,其中节点无规律运动的问题尤为突出,因此本文提出了一种新型的时间同步算法(MV-Sync),首先利用节点的运动模型与空间相关性进行节点的定位与速度测算,然后通过信标节点迭代方式完成对所有节点的时间同步工作,并推导出时间同步的参数计算方程。实验结果表明,本文算法在水下环境中具有良好的稳定性,且适用于高密度节点环境。在接下来的工作中将会进一步对误差进行修正,并从能量消耗方面做进一步优化。
