认知无人机网络中多机协作频谱感知研究
2020-06-12张宏伟达新宇王浩波
张宏伟, 达新宇, 胡 航, 倪 磊, 潘 钰, 王浩波
(1.空军工程大学研究生院,西安,710077;2.空军工程大学信息与导航学院, 西安, 710077)
无人机(Unmanned Aerial Vehicles, UAVs) 功能多样且操作方便,在危险偏远、成本较高的应用场景中越来越受欢迎,并在军事和民用领域得到广泛使用,其中包括:交通[1]、监管[2]、军事行动[3]、荒野救援[4]、商用无人机[5],灾难恢复[6]等。小型无人机重量轻,翼展相对较短,易于制造和操作,成本较低,通常低空飞行,便于密切观察地面物体[7]。多架小型无人机一起组成多机系统,通过相互协作提高可靠性和工作效率[8],这样的多机系统具有成本低和扩展性好2个主要优点[9]。不难预测,多机协同工作模式将会在未来复杂环境中得到广泛应用。
无人机主要工作在IEEE S-波段、IEEE L-波段以及工业、科学和医疗频段[10]。随着科技的发展,无线和蜂窝网络新设备急剧增加,导致无人机的工作频谱变得十分稀缺。在多机系统中,一部分无人机连接到地面基站或卫星,另外一部分无人机与其他无人机通信以便将其数据中继到基站。因此,在多机系统中,频谱稀缺问题更加严重[11]。
为了解决频谱稀缺问题,认知无线电(Cognitive Radio, CR)技术被提出,该技术使次级用户能够机会性地利用授权或非授权的频带[12]。因此,无人机次级用户(Drone Secondary User, DSU)可以利用空闲频谱继续工作,而不干扰主用户(Primary User,PU)的通信质量。由于信道衰落和噪声干扰等影响,单用户感知性能并不理想,进而提出协作频谱感知(Collaborative Spectrum Sensing, CSS)[13]。对于多机系统而言,CSS可以解决隐藏终端问题,而且随着参与CSS的DSU数量增加,感知性能可以大大提高[14-15]。
在最近的研究中,文献[16]研究无人机在实际应用中的频谱分配,文献[17]提出一种高效节能的无人机通信方案并对无人机飞行位置进行优化,文献[18]提出一种调整能量检测门限的双机协作频谱感知算法,但其信道模型并不符合无人机正常工作的实际情况。目前基于多机系统的CSS研究还比较少,考虑到上述文献提出的频谱管理方案并针对信道模型的不足,本文建立认知无人机网络(Cognitive Drone Network, CDN)模型,利用能量检测以及决策融合方法研究CSS性能,并提出一种最佳融合准则,使得CSS总错误率达到最小,最后针对大型的多机系统,提出一种快速协作频谱感知算法,该算法在保证总错误率小于某一定值的前提下,得到了CSS所需的DSU数量最小值。
1 模型建立
建立一个由K架DSU和一个融合中心(Fusion Center, FC)组成的CDN,如图1所示。为了简化模型,假设该模型中小型无人机均低空飞行,不考虑无人机通信的大尺度衰落,仅分析无人机小尺度衰落模型下的CSS性能。通常,无人机正常工作小尺度衰落信道模型为瑞利衰落信道以及Nakagami衰落信道[19]。

图1 多机协作感知模型
假设每个DSU独立执行频谱感知,然后将本地感知结果发送到FC,FC通过融合所有DSU的决策信息来推断PU空闲或存在。频谱感知过程可看作是二元假设检验问题:
H0表示主用户空闲;H1表示主用户存在。
首先考虑第i架DSU的频谱感知问题。二元假设问题如下:
(1)
式中:xi(t) 是第i架DSU的接收信号;s(t)是PU发射机的发送信号;wi(t)是加性高斯白噪声(Additive White Gaussian Noise, AWGN);hi(t)表示PU与第i个DSU之间的信道增益,假设感知时间小于信道的相干时间,因此在感知过程中,hi(t)可以认为是时不变的,由hi来表示。此外,假设在频谱感知过程中,PU状态保持不变。
在AWGN信道环境下,对于具有能量检测器的第i架DSU,由文献[20]可知,其平均虚警概率、检测概率以及漏检概率的表达式为:
(2)
(3)
Pm,i=1-Pd,i
(4)
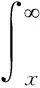
虚警概率Pf,i与感知信噪比γi无关,无论何种信道衰落,Pf,i均与AWGN信道虚警概率表达式(2)相同。所以在瑞利衰落信道下,虚警概率Pf,i保持不变,检测概率Pd,iRay表达式为[20]:
(5)
(6)
同理,在Nakagami衰落信道下,平均虚警概率Pf,i可由式(2)得到,检测概率Pd,iNak为[20]:
(7)

为了计算方便,由文献[21]知G1可表示为:
(8)

在多机协作感知中,每个DSU基于其局部检测做出二元决策,将1位的决策信息Di(1表示PU存在,0表示PU空闲)发送给FC。在FC处,根据“n-out-of-K”准则做出判决:
(9)
式中:H1和H0分别表示FC得出的PU存在或空闲的推断;CSS的决策阈值n为整数。可以得出:“OR”准则对应于n=1的情况, “AND”准则对应于n=K的情况。
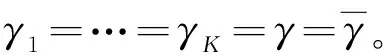
可以推导出本文模型中多机协作感知的虚警概率:
Qf=Prob{H1|H0}=
(10)
以及漏检概率:
Qm=Prob{H0|H1}=
(11)
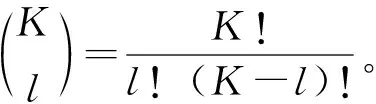
2 协作频谱感知最佳融合准则
基于前文中K架无人机CSS模型,假设无人机数量K已知,提出一种最优准则,即最佳融合准则。得到在CSS中使总错误率Qf+Qm取得最小时的决策阈值n,记为nopt。
由式(10)和(11)可知:
(12)
定义函数:
Pd)K-l],可以得到Qf+Qm=1+F(n)。由Pm=
1-Pd可知:
(13)
为求得最佳阈值nopt,令F(n)对n求偏导:
(14)
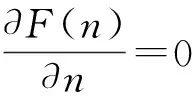
(15)
(16)
由式(16)给出的最佳融合准则,可以得到以下结论:
1)当单个DSU的虚警概率Pf和漏检概率Pm相同时,即:Prob{H1|H0}=Prob{H0|H1}时,β≈1,此时,最佳阈值nopt=K/2;
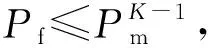
3)当β=0时,nopt=K, “AND”准则为最佳准则,此时,Pm≪Pf,即能量检测门限λ较小。
3 快速协作感知算法
对于有大量DSU的CDN,因为一个时隙只有一个DSU将其频谱感知结果发送给FC,这样FC可以很容易区分不同的感知结果,但同时也使整个感知时间过长,因此CSS在DSU数量较多时效率将会变低。允许DSU并行发送感知结果可以从一定程度上解决这个问题,但这样又会使FC的设计复杂化。另一种可行的解决方案是在正交频带上并行发送感知结果,但这需要占用大量可用带宽。为解决这些问题,本节在利用最佳融合准则的基础上提出一种适用于无人机高效工作的感知算法,该算法基于一个时隙中只有一个DSU传输感知结果,在保证感知总错误率小于某一阈值ε的条件下,仅需要部分DSU参与CSS,以解决感知时间较长的问题。
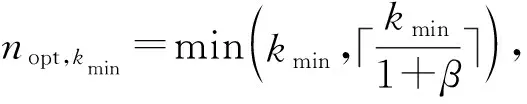
F(k,nopt,k)=Qf(k,nopt,k)+
Qm(k,nopt,k)-ε
(17)
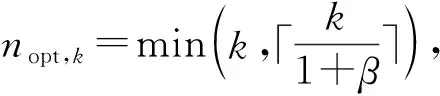
F(kmin,nopt,kmin)≤0
(18)
F(kmin-1,nopt,kmin-1)>0
(19)

(20)
该快速协作频谱感知算法在保证总错误率小于ε的条件下,得到参与CSS所需DSU数量的最小值,协作感知时间由K个感知时隙减少为kmin个感知时隙,因此,总时隙中感知时间减少,数据传输时间相应增加。
4 仿真与分析
提出的CSS优化方案可通过仿真结果评估。首先,在瑞利衰落信道以及Nakagami衰落信道(m=3)环境下,对于具有6个DSU的CDN,假设感知信噪比SNR=10 dB,由式(12)可得不同融合准则下能量检测门限与CSS总错误率的关系曲线,见图2。
由图2可知,2种信道环境下的总错误率曲线均存在唯一极小值,对应最佳能量检测门限λ,且随着λ的增加,FC的最佳决策阈值n减小。这是因为随着λ的增加,CSS的虚警概率Qf减小,漏检概率Qm增加,当λ小于最佳能量检测门限时虚警概率的减小幅度大于漏检概率的增加幅度,而当λ大于最佳能量检测门限时则相反,所以总错误率Qf+Qm呈现先减小后增加的趋势。当能量检测门限较小时,较大的决策阈值n可以克服虚警概率Qf增加带来的影响,此时,“AND”准则为最佳准则,即nopt=6。同理,当能量检测门限较大时,较小的决策阈值n可以克服漏检概率Qm增加带来的影响,此时,“OR”准则为最佳准则,即nopt=1。
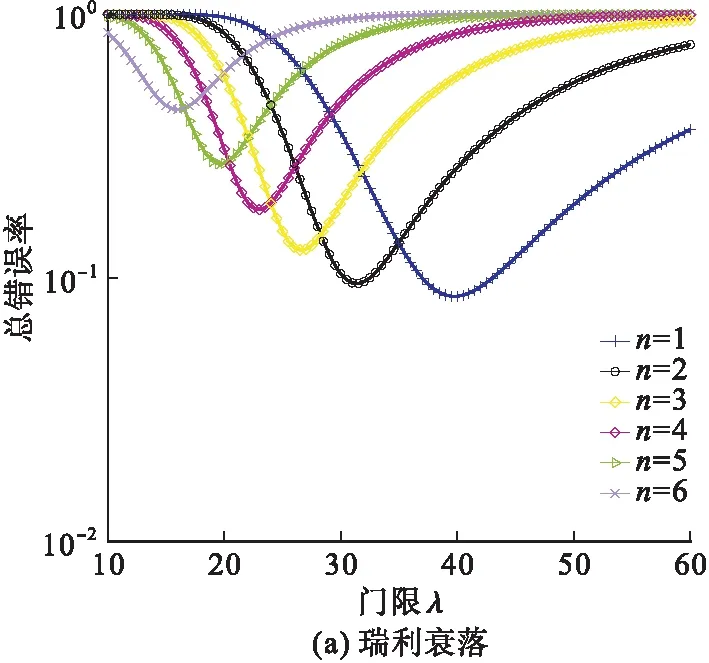
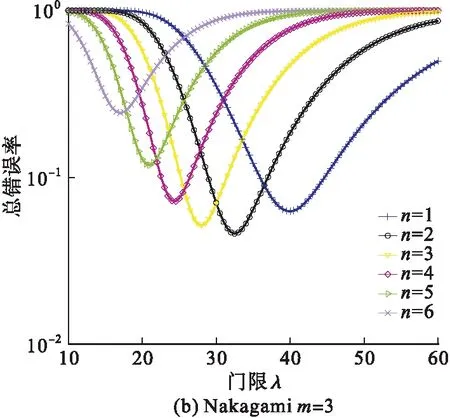
图2 K=6,SNR=10 dB, 2种衰落环境下CSS的总错误率曲线
图3给出当SNR=0,5,10,15 dB时,“OR”准则和“AND”准则在瑞利衰落环境下能量检测门限与CSS总错误率的关系曲线,由图3可知,随着SNR的增加,“OR”准则和“AND”准则的总错误率最小值逐渐减小,且总错误率最小值对应的最佳能量检测门限逐渐增加。
接下来,利用第2节中提出的最佳融合准则优化上述2种信道下的CSS总错误率。在感知信噪比SNR=10 dB,K=6的认知网络中,瑞利衰落信道以及Nakagami衰落信道(m=3)环境下能量检测门限与CSS总错误率的关系曲线见图4。
由图4可知,利用最佳融合准则,无论能量检测门限λ取何值,总可以得到与之对应的最佳决策阈值nopt,使CSS的总错误率最小。对比2种信道环境下的CSS总错误率曲线可知,当能量检测门限λ≤47.5时,采用最佳融合准则的CSS在Nakagami衰落信道(m=3)环境下性能更好,具有更小的总错误率。

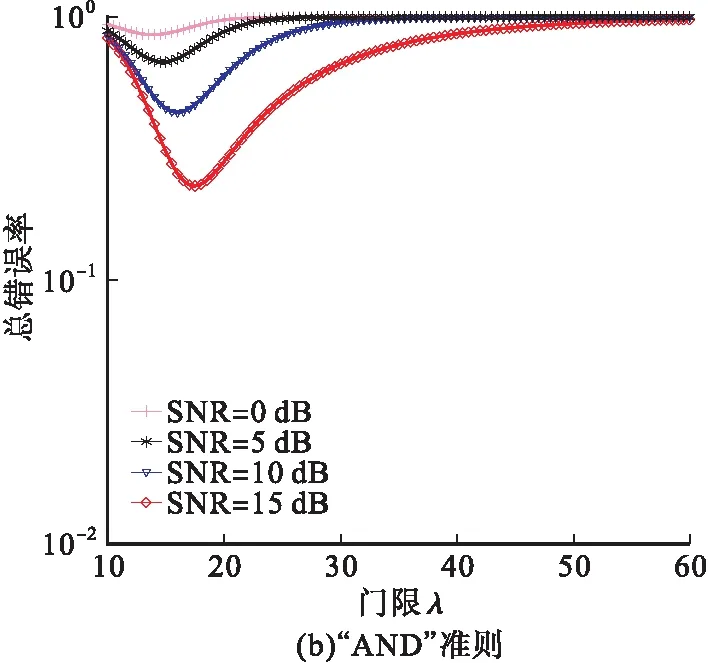
图3 K=6,瑞利衰落环境采用“OR”准则、“AND”准则在不同SNR下的总错误率曲线

图4 K=6,SNR=10 dB, 2种信道环境下采用最佳融合准则时CSS的总错误率曲线
图5给出了在能量检测门限λ=40,K=6的认知网络中,2种信道环境下分别采用“OR”准则和最佳融合准则优化得到的SNR与CSS总错误率关系曲线。由图5可知,随着SNR的增加,采用前文提出的最优准则比“OR”准则具有更小的总错误率,且当SNR>8.3时,Nakagami衰落信道(m=3)环境下具有更低的总错误率。
图4、图5中采用最佳融合准则得到的曲线均包含跳跃点,造成跳跃点存在的原因是决策阈值n取值离散,随着SNR或能量检测门限λ变化,最佳融合准则总能得到使总错误率最小的最佳决策阈值nopt,所以得到的最优曲线可以理解为由不同的离散nopt对应的总错误率曲线最佳片段连接而成,这样便在曲线片段连接处出现跳跃点。
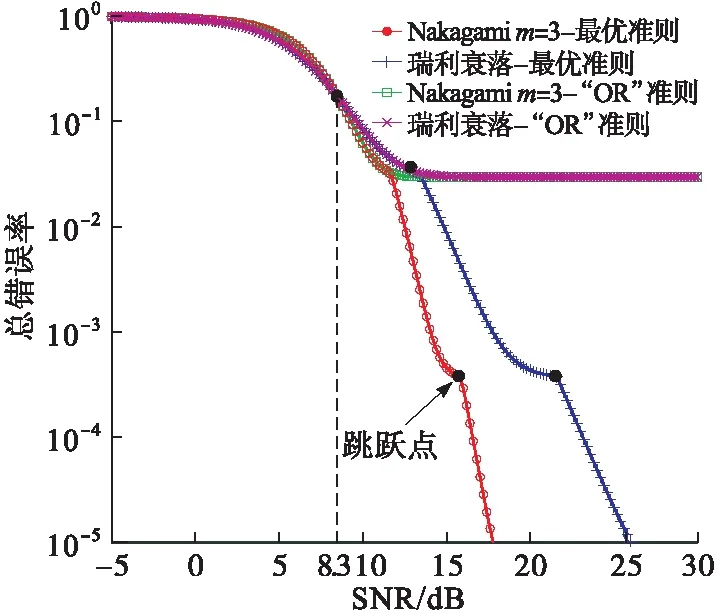
图5 K=6,λ=40,2种信道环境下采用“OR”准则和最佳融合准则时CSS的总错误率曲线
第3节提出一种仅需要部分DSU参与的快速协作频谱感知算法,假设CDN中DSU共有K=50架,感知信噪比SNR=10 dB,能量检测门限为λ=30。当阈值ε设定较大时,参与CSS的DSU数量最小值较小,CSS对感知性能的改善并不明显,反之,若阈值ε设定较小,需要参与CSS的DSU数量急剧增加,此时,对于认知无人机网络而言,较多的DSU数量将导致系统能耗增大,不符合实际的应用场景。因此,考虑到实际应用,ε的取值范围设定为10-3<ε<10-1。利用最佳融合准则(16)和满足总错误率的函数(17)仿真得出2种信道环境下,参与CSS的DSU数量最小值kmin与总错误率阈值ε之间的关系曲线,如图6所示。
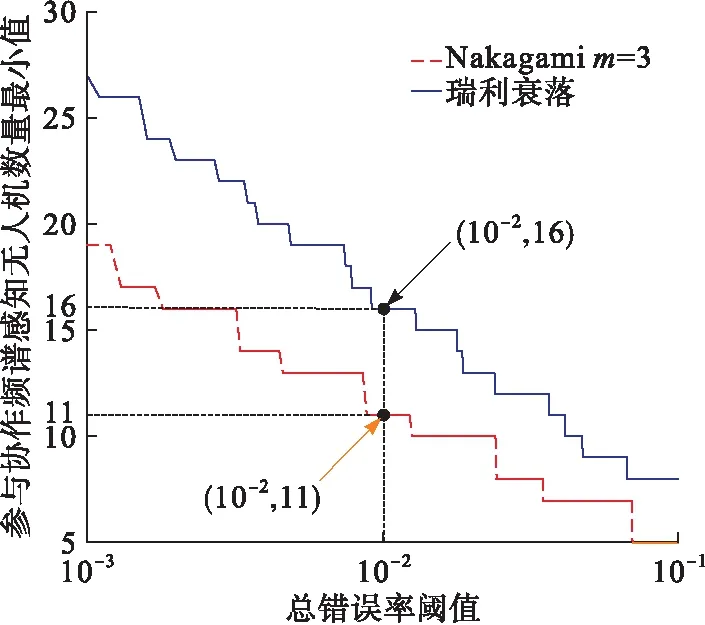
图6 K=50,SNR=10 dB,λ=30,2种信道环境下参与CSS的次级用户数量最小值kmin与总错误率之间的关系曲线
由图6曲线可知,为了使CSS的总错误率减小,需要CDN中较多的DSU参与CSS,且随着总错误率的逐渐降低,CSS所需的DSU数量最小值kmin不断增加。取ε=10-2分析算法性能,此时总错误率(Qf+Qm)≤10-2,在Nakagami衰落信道(m=3)和瑞利衰落信道环境下,参与CSS的DSU数量最小值kmin分别为11和16,因此证实了本文提出的快速协作频谱感知算法可以利用较少的DSU来保证频谱感知的检测准确度,避免了不必要的感知过程,减少了CSS的DSU数量,降低了协作感知时间,从而节省了感知过程开销。相比于瑞利衰落信道环境,该感知算法在Nakagami衰落信道(m=3)环境下性能更好,需要参与CSS的DSU数量更少。
5 结语
本文研究了在瑞利衰落信道以及Nakagami衰落信道环境下认知无人机网络的多机协作频谱感知性能,提出一种最佳融合准则,使得多机协作感知的总错误率达到最小。针对大型多机系统,本文在最佳融合准则的基础上提出快速感知算法,可以有效的减少协作感知时间,且由仿真结果可知,该算法在Nakagami衰落信道(m=3)环境下具有更好的性能。为了简化模型,本文并没有考虑无人机通信过程的大尺度衰落,在未来的研究中,将会进一步完善模型,更好地分析CDN的相关特性。
