广义四元数群上的3度1-匹配bi-Cayley图
2020-06-11吕宝栋
李 圆,王 丽,吕宝栋
(河南理工大学数学与信息科学学院, 河南焦作 454000)
0 引言
本文所涉及的图均指有限、 简单、 连通、 无向图.对于图X, 我们用V(X)、E(X)、 Aut(X)分别表示图的顶点集、 边集和全自同构群.定义群G关于子集S(不含单位元)的Cayley图记为X=Cay(G,S),其中点集为G,边集为{(g,sg)|g∈
G,s∈S}.定义群H上关于集合R,L和S的bi-Cayley图,记为BiCay(H,R,L,S), 点集为H0∪H1;边集为{{h0,g0|gh-1∈R}∪{{h1,g1|gh-1∈
L}∪{{h0,g1|gh-1∈S},其中R,L和S是H的子集,满足R-1=R,L-1=L且R∪L中不包含H的单位元,Hi= {hi|h∈H},i= 0,1.特别地,若|S| = 1,则称BiCay(H,R,L,S)是1-匹配bi-Cayley图;若|R| =|L|=s,则称BiCay(H,R,L,S)是s-型bi-Cayley图.称一个群为广义四元数群,如果满足关系Q4n=〈a,b|a2n= 1,b2=an,b-1ab=a-1〉.

本文若未有定义而引用的概念和记号可查阅文献[8].
1 预备知识
设X= BiCay(H,R,L,S)是群H关于其子集R,L,S的bi-Cayley图, 记A= Aut(X). 广义四元数群Q36的定义关系如下:
Q36=〈a,b|a18= 1,b2=an,b-1ab=a-1〉.
易知Q36中的元素可写成aibj的形式, 其中i= 0,1,…,17;j= 0, 1.
引理1[7](1)H由R∪L∪S生成.
(2)在图同构意义下,S可包含群H的单位元1.
(3)对任意α∈Aut(H),
BiCay(H,R,L,S)≅BiCay(H,Rα,Lα,Sα).
对任意g∈H, 定义点集V(X)的置换:R(g)∶hi|→(hg)i, 任意i∈Z2,h∈H. 令δα,x,y∶h0|→(xhα)1,h1|→(yhα)0,任意x,y,h∈H,α∈Aut(H),则δα,x,y是V(X)的一个置换. 此外,用Av表示点v∈V(X)稳定子群.

引理3[8](Frattini论断) 设G传递作用在集合Ω, 并且G包含一个子群N,则N在Ω上的作用传递当且仅当G=GαN, ∀α∈Ω.
引理4[8]若对图X中任意两点u,v∈E(X),总存在一个自同构φ∈Aut(X)使uφ=v成立,则X为点传递图. 若X中任意两条边{u1,v1},{u2,v2},总存在一个自同构φ∈Aut(X)使{u1,v1}φ=
{u2,v2}成立,则X为边传递图.若图X(X无向或有向)没有孤立点,且Aut(X)在X的弧集上的作用是传递的, 则X为弧传递图.弧传递图也称为对称图.
在一个图中,我们用Ni(v)表示与顶点v距离为i的点的集合,称为点v的i步邻域.特别地,N(v)表示点v的邻点的集合.
根据广义四元数群Q36的定义关系和bi-Cayley图的定义, 经简单计算可知广义四元数群上的3度1-匹配bi-Cayley图有以下两类:
(1)R1={a,a-1},L1={b,b-1},S={1};
(2)R2={ab,(ab)-1},L2={b,b-1},S={1}.
2 主要定理
定理1设X1=BiCay(Q36,R1,L1,S) ,R1={a,a-1},L1={b,b-1},S={1}是Q36上的3度1-匹配bi-Cayley图.则有以下性质: (1)X1是非点传递的; (2)X1是非边传递的;(3)X1是非弧传递的.
证明(1)由图1可知,过点11只有一个4圈即[11,b1,(a9)1,(a9b)1,11], 过点10没有4圈,故图X1不是点传递的;
(2)由图1可知,边{11,b1}∈E(X1)包含在一个4-圈[11,b1,(a9)1,(a9b)1,11]中,而边{a0,(a2)0}∈E(X1)显然没有被包含在任何一个4-圈中, 故可知X1不是边传递的;
(3)由(1), (2)立得.证毕.

图1bi-Cayley图X1=BiCay(Q36,R1,L1,S)的导出子图
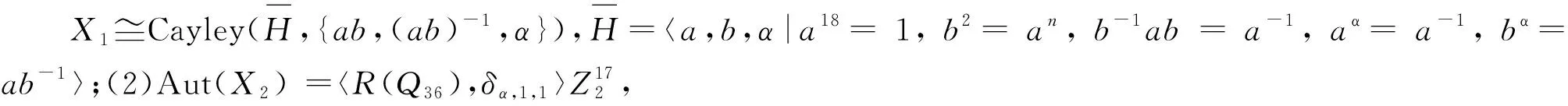
证明(1)设α∶a|→a-1,b|→ab-1, 易知
α∈Aut(H),aα2= (a-1)α=a,bα2= (ab-1)α=a-1ba-1=b.故o(α) = 2. 进而有o(δα,1,1)=2.下证δα,1,1∈I.由定义只需证
R2α= {ab,(ab)-1}α=
{a-1ab-1, (a-1ab-1)-1} = {b-1,b} =L2.
L2α= {b,b-1}α= {ab-1, (ab-1)-1} =
{(ab)-1,ab} =R2.
Sα= {1} =S-1.

(2) 由图2可知,N(10)中的三点位于两个4-圈,即点(a10b)0, (ab)0在四圈[10,(a10b)0, (b2)0, (ab)0,10]中, 点11在4-圈[11,(a9b)1, (b2)1,b1,11],又|N((b2)0)∩N(10)|=2, |N(u)∩N(10)|=1, |N((b2)1)∩N2(10)|=3, |N(v)∩N2(10)|=1或2, 其中u∈N2(10),v∈N3(10). 故可知点11,(b2)0, (b2)1固定.不失一般性,下面分两种情况考虑φ∈A10对点(a10b)0与(ab)0的作用.
若φ固定(a10b)0与(ab)0, 则(a10b)1与(ab)1也固定,(a17)1与(a8)1可互换也可固定;
若φ互换(a10b)0与(ab)0, 则(a10b)1与(ab)1也互换,(a17)1与(a8)1可互换也可固定;
故φ中必有〈((a10b)0, (ab)0)((a10b)1,(ab)1)〉, 再考虑(a17)1与(a8)1.
若φ固定(a17)1与(a8)1, 则(a17)0与(a8)0也固定,(a11b)0与(a2b)0可互换也可固定;
若φ互换(a17)1与(a8)1, 则(a17)0与(a8)0也互换,(a11b)0与(a2b)0可互换也可固定;
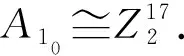

图2bi-Cayley图X2=iCay(H,R2,L2,S)
定理3Bi-Cayley图X2有以下性质:
(1)Bi-Cayley图X2是点传递的;(2)Bi-Cayley图X2是非边传递的;(3)Bi-Cayley图X2是非弧传递的.
证明(1)由定理2(1)知,X2同构于一个Cayley图,故X2是点传递的.
(2)在bi-Cayley图X2中,由定理2(2)知, |Aut(X2)|=|〈R(Q36),δα,1,1〉Z217|=36×2×217,而bi-Cayley图X2有108条边,显然108+36×2×217,所以bi-Cayley图X2不是边传递的;
(3)由(1)和(2)立得.证毕.
推论4设X1=BiCay(H, {a,a-1},{b,b-1},{1}),X2=BiCay(H, {ab,(ab)-1},{b,b-1}, {1}).则X1X2.
证明由定理1和定理3知, 图X1是非点传递的,图X2是点传递的, 故X1X2. 证毕.
