分数阶自适应P-Laplace方程在图像去噪中的应用

林雪华， 陈雁冰

(1.福州职业技术学院阿里巴巴大数据学院， 福建福州 350108；2.福建师范大学福清分校电子与信息工程学院， 福建福清 350300)

0 引言

数字图像在获取和采集过程中经常会被各种来源的噪声干扰， 不仅使数字图像的视觉效果变差， 而且增加了图像后续处理的难度. 因此， 去噪是数字图像处理重要的一个环节. 国内外学者针对图像去噪进行大量的研究， 提出了中值滤波、维纳滤波、均值滤波、低通滤波等去噪算法[1]， 但这些算法在去噪的同时也使图像的边缘和纹理信息丢失， 图像变得模糊. 因此， 如何能够在去除噪声的同时保留图像的边缘和纹理信息是图像去噪的难点.

分数阶微积分自Leibniz和Newton提出后， 至今已经300多年. 自Mandelbrot[1]发现了分形后， 分数阶微积分引起了工程技术领域的关注. 分数阶微分在处理图像纹理方面比整数阶更精细， 使其在信号分析与图像处理领域迅速发展. 目前， 国内外一些学者已经在图像边缘检测与提取[2]、图像去噪[3]、图像纹理细节处理[4]、图像修复[5]等领域取得一些研究成果.

1 理论基础及模型构造

1.1 自适应P-Laplace扩散去噪模型构造

学者Perona和Malik[6]针对能量泛函的Euier方程问题提出了各向异性扩散方程来求解该方程问题， 如式(1)所示.

(1)

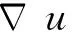
分数阶微分具有弱导性和非线性等特征， 较整数阶微分更适合处理纹理等细节信息. 将频域分数阶微分算子， 推广应用于自适应P-Laplace扩散去噪模型， 构造分数阶能量泛函：

(2)

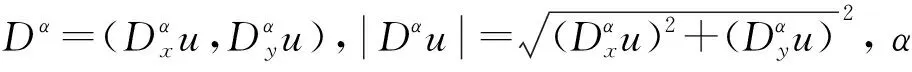
1.2 分数阶扩散因子的分析

分数阶自适应扩散因子由下面等照度线的分数阶曲率和分数阶梯度共同决定.

(3)

其中curvα的代数关系为

(4)

不同情形下分数阶扩散因子的理论分析：

(1)当P为常数时， 分数阶曲率与分数阶梯度成正比. 当分数阶曲率趋于零或当分数阶梯度趋于无穷大时， 此时分数阶扩散因子则趋近于 1， 这时各向异性扩散的特性为仅沿等照度线方向扩散， 即沿边缘方向扩散， 且不会在梯度方向扩散. 此时， 在梯度方向的平滑作用被削弱， 从而实现图像细节的保留；当分数阶梯度趋于零或分数阶曲率趋近无穷大时， 则分数阶扩散因子趋近于2， 此时各向同性扩散的特性为梯度方向和的沿等照度线方向的扩散率相同， 从而实现快速平滑.

(2)等照度线的分数阶曲率为固定值时， 在图像的边缘区域， 分数阶扩散因子随分数阶的梯度的增大而减小.

(3)当分数阶梯度为定值时，P随分数阶曲率的增大而增大.

根据以上分析， 分数阶自适应扩散因子P能够根据图像局部的几何信息合理地控制扩散因子的扩散方向及强度.

2 算法的实现

假设输入：u0， 迭代次数K， 迭代步长Δt， 输出：un+1. 在频域离散求解分数阶各向异性扩散的自适应P-Laplace方程的图像去噪模型算法流程：

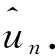
2)计算如下阶中心差分(5).

其中ω1,ω2∈{0,1,…,n-1}分别为对应空间域变量x和y的离散傅里叶变换所得的频域变量，F表示二维离散傅里叶变换，F-1表示二维离散傅里叶逆变换.

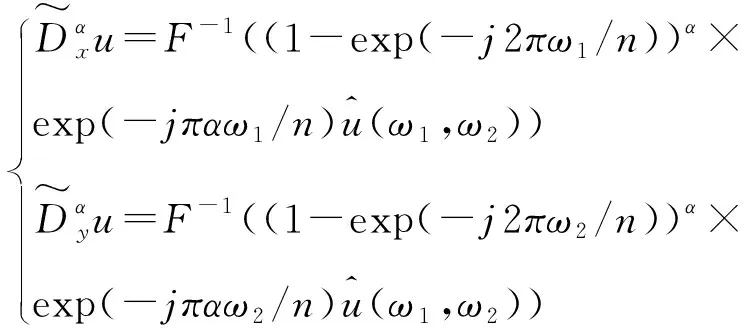
(5)

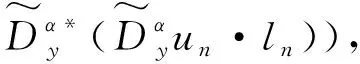
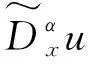
5)计算频域如公式(6)所示.

(6)

令K1为一个频域对角矩阵， 定义为

K1=diag((1-exp(-j2πω1/n))αexp(-jπαω1/n))

(7)

(8)

exp(-j2πω1/n))αexp(-jπαω1/n)))

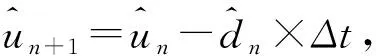
3 实验结果及分析

为验证本文算法的正确性和有效性， 本文采用Visual Studio 2017为开发环境， 以大小为256×256像素， 高斯白噪声均值μ=0，σ2=0.06的灰度Camera图像作为测试图像. 图1是采用分数阶自适应P-Laplace扩散模型的不同迭代次数的去噪处理后的图像.

表1为分数阶自适应P-Laplace扩散模型不同迭代次数的去噪处理后图像的信噪比和均方误差的数值比较. 从实验数据来看， 虽然各个不同迭代次数处理后数据的差别不是很大， 但还是可看出迭代12次的信噪比高于其他次数.迭代是多次的傅里叶变换与傅里叶逆变换， 若设置迭代次数越多， 则处理时间会越久， 而处理后的图像也会变得模糊. 所以， 在本节研究的分数阶自适应处理时不必设置过多迭代次数， 通常设置在10到15次间即可. 从视觉观察上来看， 该算法平滑了图像里人物的头发和衣服， 较好地去除了噪声， 图像中一些细节轮廓也得到较好保留. 且该模型不仅能较好地保持图像中平坦区域的低频分量， 还能非线性地保持图像中灰度值变化较大区域的高频分量， 如相机的弯曲边缘等. 此外， 对图像中灰度值变化不明显的区域， 如远处的建筑里细小的尺度纹理及灰度值均匀变化里的区域坡度信息有一定增强.

图1 不同迭代次数处理后的图像对比

表1 本文算法不同迭代次数处理后的数值比较

为了进一步对传统去噪算法、自定义分数阶和本文算法处理后图像的效果进行比较， 选一幅细节特征较多的图像进行处理， 如图2所示. 从视觉观察角度看， 中值滤波仅是对脉冲噪声具有良好的抑制作用， 处理高斯噪声图像会严重模糊图像的整体信息；均值滤波模板滤除噪声的代价就是会模糊图像， 很明显图像中的水流、树林、桥的整体结构都被模糊了；维纳滤波去噪过程产生振铃而导致处理效果不好；高斯去噪虽有去除噪声， 一定程度上提高了图像的整体亮度， 但并没有达到最佳效果. 表2为不同类型去噪算法的信噪比和均方差比较. 从数据看， 不管是自定义分数阶去噪算法还是本文的分数阶自适应P-Laplace方程的信噪比和均方差都明显高于传统的几种去噪算法， 能够达到保留更多图像的纹理细节信息及最佳视觉效果的目的. 自定义分数阶去噪算法整体提高了图像亮度， 能够较好地体现图像信息， 例如对于水流部分能够完整地体现出来， 但树林部分却有些模糊. 本文算法PSNR在几种算法中值最高， 从视觉角度看去噪效果最好， 能够在滤除噪声的同时， 对于图像中桥的整体结构， 栏杆部分， 水流部分和树林树枝的纹理都能较清晰地体现出来， 达到尽可能多地保留图像中细小局部特征的效果.

图2 传统算法与本文算法处理后的图像

表2 不同类型去噪算法处理后的数值比较

4 结论

本文提出将分数阶自适应P-Laplace方程应用于图像去噪的算法. 该算法模型根据频域定义来确定分数阶的扩散因子和分数阶导数， 且利用分数阶等照度线的曲率及分数阶梯度共同自适应地调整分数阶扩散因子. 该算法能够根据图像的噪声分布自适应地运用更合适的阶次来滤除噪声， 并且结合迭代的方式以实现对噪声图像的微调.