基于Bradley-Terry模型的CBA联赛夺冠问题方案设计

许佰雁

(长春光华学院基础教研部， 吉林长春 130033)

中国男子篮球职业联赛创办于1995年， 是中国最高等级的篮球联赛. 球队的胜率和综合水平问题是大家所关心和关注的， 本文在借用模型的基础上对14支队伍的常规赛和季候赛进行分析， 估算出每只球队夺冠概率， 预测出前四名的球队.

1 模型建立与求解

1.1 基本假设

1) 假设比赛是公平的， 且每次比赛球员都尽全力.

2) 假设所有球队得到的休息时间是一样的.

3) 假设每个教练的水平都差不多， 能够合理分配每个球员的时间

4) 假设外界因素的影响为零.

1.2 模型建立

设有n个球队参与比较， 记为“A,B,C…,n”， 假设球队i有真实的能力参数γi， 令pi,j表示球队i优于球队j的概率，Yij表示球队比较后的二分变量结果. 当Yij=1时表明球队i比j好， 当Yij=0时表明球队j比i好.

将pi,j表示为Logit模型：

或者

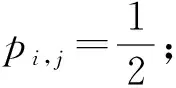
令Nij表示进行比较的总次数， 其中所选择到球队i的次数为nij， 选择球队j的次数为Nij-nij.

当Nij独立， 且每次的概率都为Pi,j时，nij服从二项分布bin(Nij,Pi,j). 根据研究对象服从二项分布建立函数进行估计， 如果有关不同配对的比较也是独立的， 就可以利用拟合普通的Logit模型的方法来拟合这个模型.

1.3 模型求解

对调查数据表中给出的每队的数据进行分析， 通过一个具有说服性的数据来预测出排名. 每队各给出了100组比赛的历史评分数据， 求出各队的平均值， 如表1所示.

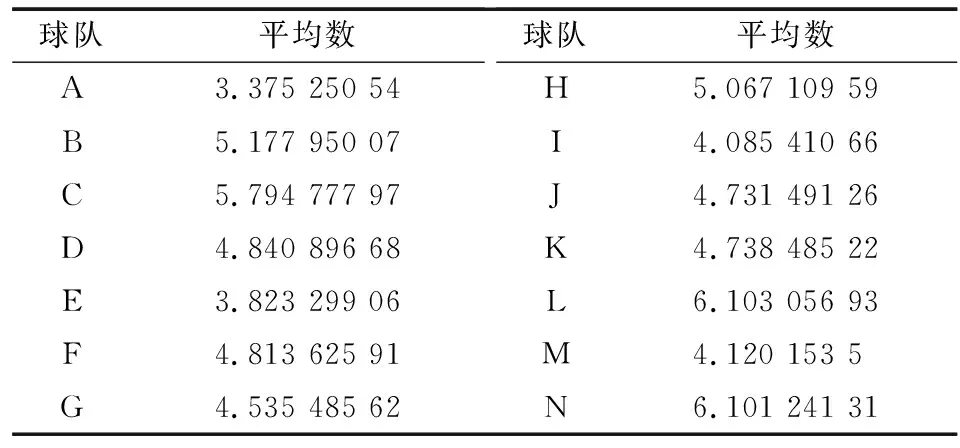
表1 14组队伍综合实力水平的平均值

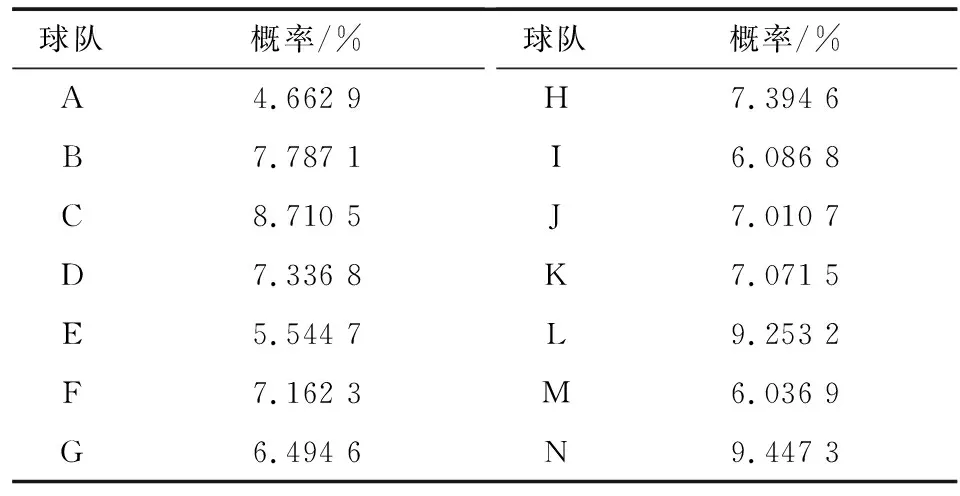
表2 队伍概率结果

然后通过平均值求出方差和标准差(见表3)， 方差是

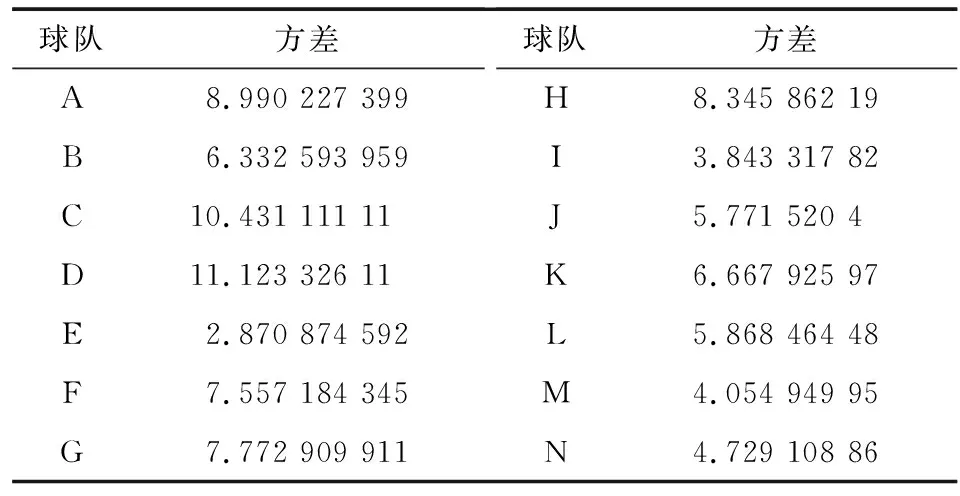
表3 14组球队综合实力的方差

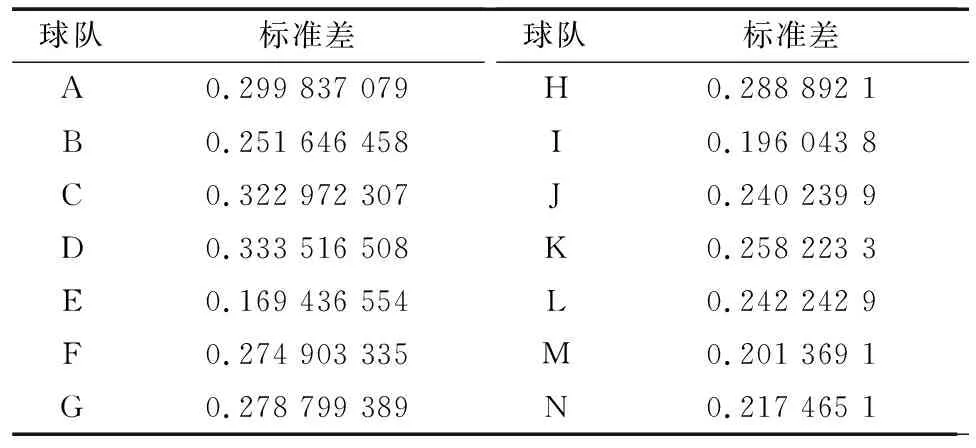
表4 14组队伍综合实力的标准差

通过对z值的比较可以得出前四名的球队分别是N、L、C、B. 再分析实力估计值、 标准误值、 拟标准误值这些数据可以得出结论： 第一名是N队， 第二名是L队， 第三名是C队， 第四名是B队.

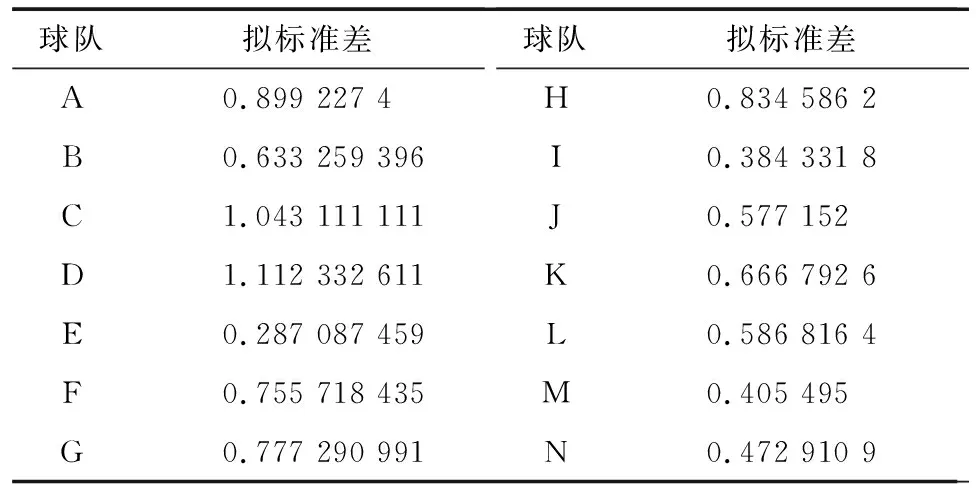
表5 14组队伍综合实力水平的拟标准差

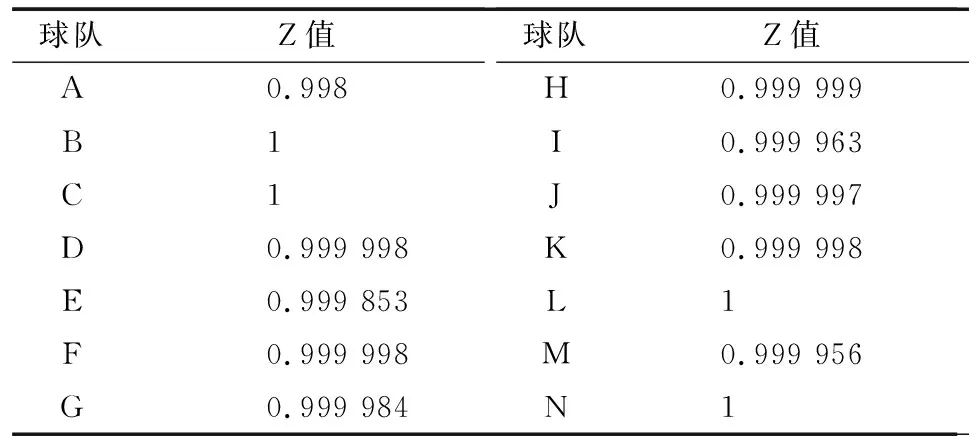
表6 14组队伍综合实力水平的Z值

2 模型检验与评价

2.1 针对2015～2016 赛季CBA联赛球队实力估计结果

用所给出的各队实力估计值求出平均值， 再运用方差和标准差公式

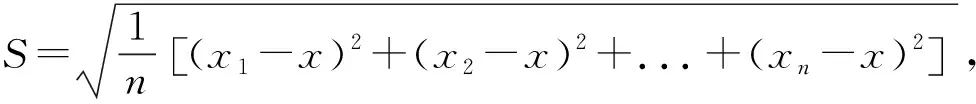
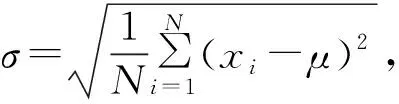
通过对z值的比较和对实力估计值、 标准误差值、 拟标准差值这些数据的分析可以得出队伍的排名. 结果与模型中的公式计算结果相同.

2.2 模型评价

(1)优点

1)该方法下的赛事安排更合理， 计算数据较为准确， 进行最后的比较和分析更具说服力. 该模型对数据的精确性有较高的要求.

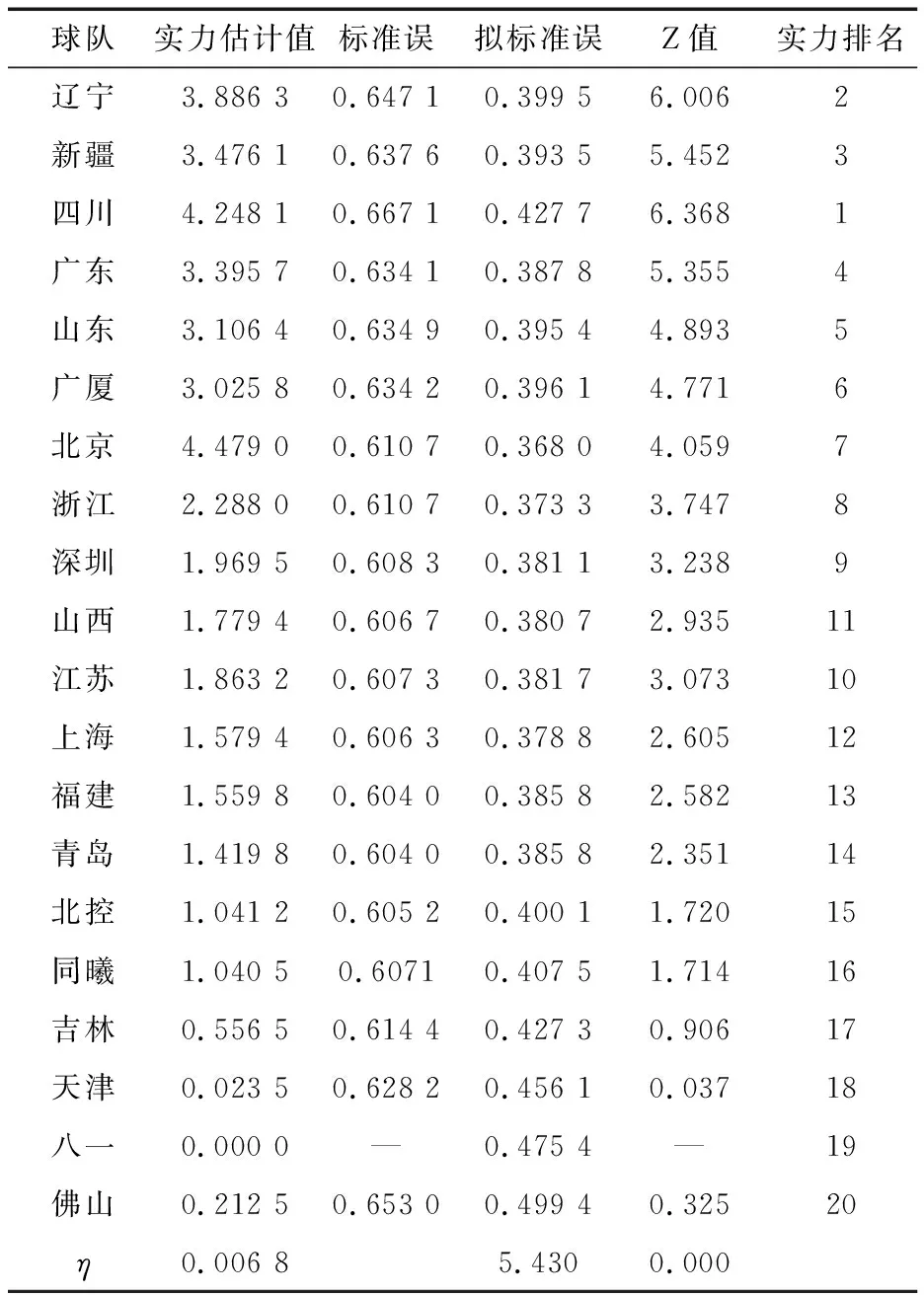
表7 2015～2016赛季CBA联赛球队实力估计结果

2)本次结合了大量文献综合分析了Bradley-Terry模型的原理和算法， 结合数据分析， 将模型运用到了体育赛事中， 并成功预测了参赛队伍的排名.

(2) 缺点：

1)该模型对于较少数量的球队数不适用， 适用于求大型比赛的结果. 别外， 该模型较为繁琐， 不够简便.

2)该模型使用起来的数据分析结果可能只是在此赛季是显著的， 其他赛季是否显著， 还需要进一步研究.

3)该模型虽然提出了在体育赛事的实力会发生变化， 但理论上尚未健全， 未能使用统计软件结合数据进行实战分析， 仍有较大提升空间.

2.3 模型推广

该模型可运用于对统计学期刊影响力的估计或者与机器学习搜索引擎相关的文件进行排名， 也可应用于研究人们对某种对象的偏好情况， 通过对模型的拓展可以解决分类数据的分析问题. Bradley-Terry模型提高了关于成对比较数据的准确性和有效性， 它可以基于过去的对比信息来预测将来事件比对的结果. 所以Bradley-Terry模型不但有力地推动了成对比较法， 而且在很多研究领域乃至日常生活中， 都有着不可忽视的地位.