双加权伪概周期随机过程空间的等价性

朱 平

(洛阳师范学院数学科学学院， 河南洛阳 471934)

在现实世界中， 各种干扰因素可能会改变事物的周期运动规律， 甚至使其周期性发生变化. 因此， 自然现象的概周期性研究比周期性更符合实际， 例如能更准确地预测日食以及月食发生的地点等信息.

在概周期函数的基础上， 张传义教授提出伪概周期函数， 该函数可分解为概周期函数与无穷远处时间平均为零的函数之和[1]. 2006年， 针对伪概周期函数的扰动部分， 在权函数ρ的作用下提出加权伪概周期函数[2]. 近年来， 加权伪概周期函数及其推广已应用到不同类型的微分方程[3-4]. 但是当两个不等价的权函数共同作用时， 在均方意义下的加权伪概周期随机过程尚未研究， 因此， 本文提出均方双加权伪概周期随机过程的定义， 并从不同角度研究其空间的等价性. 该研究具有重要的理论和实际意义.

1 基本知识

称ρ为权函数, 如果ρ局部可积且几乎处处大

于0, 所构成的集合用U表示. 对r>0,定义

则下列定义成立.

定义1[3]连续随机过程X∶R→L2(P,H)称为是概周期的， 若对每ε>0,存在l(ε)>0,使得任意长度为l(ε)的区间内， 至少存在一个τ使得

记AP(R,L2(P,H))表示所有这样的随机过程构成的集合.

定义2[4]令ρi,qi∈U∞, 称均方连续有界的随机过程X∶R→L2(P,H)是双加权遍历扰动的， 如果

记PAP0(R,L2(P,H),ρ,q)为该类随机过程构成的集合.

定义3称随机过程X∶R→L2(P,H)是双加权伪概周期的， 若X=X1+X2, 其中

X1∈AP(R,L2(P,H)),

X2∈PAP0(R,L2(P,H),ρ,q).

记WPAP(R,L2(P,H),ρ,q)为所有这样的随机过程构成的集合.

2 主要结果

对任意集合A， 用AC表示该集合在R中的补集， 则下列结论成立.

定理1令ρi,qi∈U∞， 且存在可测集A0∈R和常数mi,Mi>0(i=1,2)使得

则

WPAP(R,L2(P,H),ρ1,q1)=

WPAP(R,L2(P,H),ρ2,q2).

证明由定义3可知， 只需证

PAP0(R,L2(P,H),ρ1,q1)=

PAP0(R,L2(P,H),ρ2,q2).

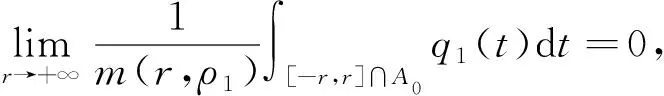
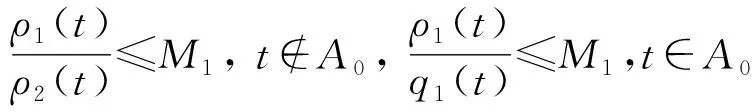
(1)

因此

结合条件f∈PAP0(R,L2(P,H),ρ1,q1)、 (1)和

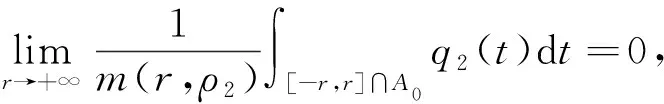
f∈PAP0(R,L2(P,H),ρ2,q2)

类似地， 我们可证结论

PAP0(R,L2(P,H),ρ2,q2)⊆PAP0(R,L2(P,H),ρ1,q1).

定理2令ρi,qi∈U∞(i=1,2)， 且存在常数

0<α<1和可测集A0∈R, 使得

(2)

(3)

其中Ar={t∈R∶αr≤|t|≤r},

(4)

(5)

则

WPAP(R,L2(P,H),ρ1,q1)=

WPAP(R,L2(P,H),ρ2,q2).

证明由定义3可知， 只需证

PAP0(R,L2(P,H),ρ1,q1)=

PAP0(R,L2(P,H),ρ2,q2).

对任意的h∈PAP0(R,L2(P,H),ρ1,q1)， 令

利用Ar={t∈R∶αr≤|t|≤r},可得

(6)

通过计算， 则

利用(3)和(4)， 有

(7)

结合(6)和(7)， 可推出

因为

且

从而

即h∈PAP0(R,L2(P,H),ρ2,q2).

类似地， 可证

PAP0(R,L2(P,H),ρ2,q2)⊆

PAP0(R,L2(P,H),ρ1,q1).

推论1. 令ρi,qi∈U∞(i=1,2)， 且存在常数

α>1和可测集A0∈R, 使得

其中Ar={t∈R∶r≤|t|≤αr},

则

WPAP(R,L2(P,H),ρ1,q1)=

WPAP(R,L2(P,H),ρ2,q2).