NURBS曲面细分建模技术的研究与实现

孔令德， 康凤娥

(1. 太原工业学院计算机工程系, 山西太原 030008; 2.太原工业学院电子工程系, 山西太原 030008)

0 引言

NURBS曲面是在de Boor三次样条曲面插值的基础上， 加入了张量积曲面定义的一种曲面， 其在构造CAGD曲面中较为常见[1]， 其形状都是矩形域的. 随着CAGD曲面的应用范围不断扩大， 单个矩形域已不能满足实际建模的需求， 特别是在CG动画制作的领域， 前期的曲面拼接技术与裁剪技术在复杂CG模型中的构建是不容易实现的. 因此， 笔者提出了细分曲面技术. 细分曲面不需要切割、不需要关节连接的特性可以解决曲面裁剪与拼接的问题. 它可以在任意拓扑网格上构造光滑的表面.

最早的细分算法是图形艺术家Chaikin在1974年CAGD国际会议上提出的、 用于快速生成一条光滑的曲线的多边形割角算法[2]. 1978年， Catmull 和Clark 提出了CatmullClark细分曲面， 是对任意拓扑网格上的三阶齐次B样条曲面的扩展[3]. 同年， Doo 和Sabin 也提出了Doo Sabin细分曲面， 是对任意拓扑网格上双均匀B样条曲面的扩展[4]. 这两种细分曲面的提出标志着这一新曲面形式的出现. 1987年， Loop将四次三项样条推广到任意的三角网格上， 构建出了基于三角网格的Loop细分曲面[5]. 在三角网格方面， Dyn和Levine则利用四点插值的细分方法， 构建了基于三角网格插值的蝶形曲面(Buterfly surface)[6]. 1998年， Sederberg、Zheng和Sewell等人将节点距方法引入细分曲面构建中， 获得了两种非均匀有理细分曲面——广义的CatmullClark细分曲面(NURCCs)和广义的Doo-Sabin细分曲面[7]. 2003年， Sederberg、Zheng和Bakenov等人利用T控制点改善了NURCCs， 在T-NURCCs中实现局部插入T控制点方法[8]. Stam给出了Catmull-Clark细分曲面精确的计算方法， 实现通过细分曲面可以精确计算为任意参数的参数曲面[9].

细分曲面理论在学术界不断地深化与完善， 细分曲面作为CG动画制作的一种有效的曲面造型方法也在商业界不断被使用. 许多三维建模系统， 如开源软件Brand、Pixar公司的Renderman和FEDES Effice公司的Houdini， 已经在其建模系统中添加了细分曲面技术. 细分曲面技术已经成为CG动画制作的行业标准.

本文根据细分曲面的原理， 给定了一个初始的多边形网格信息， 并通过定义细分规则不断在已有网格上插入新的控制顶点， 然后将多边形网格多次进行细化， 最后得到了一张具有光滑连续性的曲面.

1 曲面建模相关技术

1.1 NURBS曲线曲面

NURBS是一种非均匀有理B样条(Non-Uniform Rational B-Spline)， 是几何建模领域一种建模方式. 1946年Schoenberg提出了B样条的理论[10]， B样条方法具有建模的许多优势， 其缺点是不能适应初等曲面的要求， 而NURBS方法很好地解决了这一问题[11].

一条k次NURBS曲线可以表示为一分段有理多项式矢函数

(1)

式(1)中wi(i=0,1,…,n)被称为权重或权重因子(权重)， 它们分别与控制点di(i=0,1,…,n)相对应， 一个控制顶点对应着一个权因子. 首末权因子要求大于0， 其余大于或等于零. 同时要求顺序k个权因子不能同时为零. 由控制顶点di连接起来组成NURBS的控制多边形.Ni,k(u)是k次规范B样条基函数， 和B样条一样， 是由节点矢量U-[u0,u1,…um+k+1]按德布尔-考克斯递推公式决定的[12-13]. 实际应用中， 将NURBS开曲线节点矢量两端节点的重复度取为k+1， 即u0=u1=…uk，un+1=un+2=…un+k+1. 曲线定义域常取为u∈[uk,un+1]=[0,1].

在U方向和V方向， 使用NURBS曲线的方法， 构造一张NURBS曲面， 一张k×l次NURBS曲面， 其曲面可以表示为

(2)

(2)中， (u,v)∈[0,1]×[0,1]，wij是控制权因子， 规定四角顶点处使用正权因子， 即w00、wm0、w0n、wmn>0， 其余wij≥0且顺序k×l个权因子不同时为零. 控制顶点dij(i=0,1,…,m)(j=0,1,…n)按矩阵排列， 形成一个m×n的控制网格. 和B样条一样， 一个顶点dij对应一个控制权因子wij. NURBS曲面的Ni,k(u)(i=0,1,…,m)和Nj,l(v)(j=0,1,…,n)分别为u向k次和v向l次的规范B样条基. 它们分别由u向和v向的节点矢量U=[u0,u1,…,um+k+1]与V=[v0,v1,…,vn+l+1]按de Boor-Cox递推公式决定.

1.2 几种细分建模技术

常用细分算法有Catmull-Clark细分、Loop细分、蝶型细分、Doo-Sabin 细分、T样条细分等.

(1)Catmull-Clark双三次B样条细分

Catmull-Clark的细分算法是基于双三次B样条的计算机图形细分建模技术， 是一种光滑表面细分曲面建模的算法. 它由Edwin Catmull和Jim Clark在1978 年设计， 并将双三次均匀B样条曲面推广到任意拓扑结构层面上.

(2)Loop细分

Loop细分是由Charles Loop于1987年为三角网格开发的近似细分规则[14]. 它被划分成1～4个三角形， 每个边都通过计算生成一个新的顶点， 并且每个原始顶点被更新.

(3)蝶形细分

Dyn、Gregory和Levin首先提出了蝶形插值细分的算法[4]， 细分算法可以在规则区域获得光顺次序但是边缘的平滑度降低， 连接到一个点的边缘的数量被称为奇点附近的点的人类程度. 如果一个内点的人度不为6或者一个边缘点的人度不为4， 则称这样的点为奇异点， 否则称为规则点[15]. Denis Zorin改进了Dyn、Gregory和Levin的细分规则[16]， 他在奇异点周围定义了新细分的规则， 使得细分面片在奇异点周围也具有光滑的连续性. 但是他的算法在用于处理一般的三维网格的时候， 细分出来的面片效果很差， 达不到设计人员的要求， 究其原因是细分面片的光顺性很差， 进而严重影响了细分面片的视觉效果.

(4)Doo-Sabin 细分

Doo-Sabin细分算法是二次均匀B样条曲面二分技术的推广， 它由Daniel Doo和Malcolm Sabin于1978年开发[17]. 与Loop细分算法相比， Doo-Sabin细分算法的控制网格是四边形.

(5)T样条细分

Sederberg等人提出了T样条的局部细分算法[18-19]. T样条局部细分的思想是在T网格插入一个或多个控制点而不改变T样条的曲面形状. 因为插入一个控制点到T网格中必须伴随着将节点插入到相邻的混合函数中， 这一方法被称为局部节点插入. .

2 NURBS插入节点细分规则

结合前述对细分建模的研究和实践， 本文选择NURBS插入节点技术作为实现曲面细分建模.

2.1 NURBS曲线插入一个节点

在NURBS的曲线中插入一个节点， 即在NURBS曲线定义域的某段节点区间插入一个节点u∈[ui,ui+1]⊂[uk,un+1]， 则新节点的矢量为

U=[u1，u1, …,ui,u,un+1, …,un,un+k+1]

重新进行编号后变为

(3)

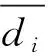
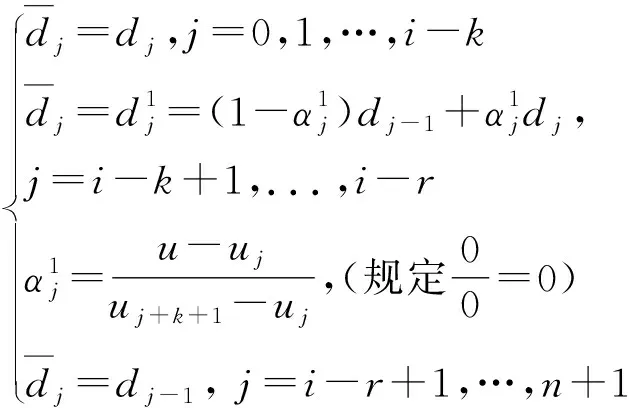
(4)

公式(4)中r参数代表将要插入的节点u在原节点矢量U中已经存在的个数.

2.2 NURBS曲线重复插入同一个节点

在节点矢量中重复插入l次同一节点u， 即在节点矢量中插入重节点. 而将要插入的节点u在原节点矢量U中已经存在的个数为r， 也就是已有ui=ui-1=…=ui-r+1， 要求r+l≤k. 这时新的节点矢量

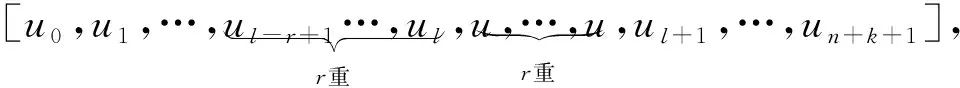
2.3 NURBS曲面插入节点

NURBS样条曲面由节点矢量U和V决定，U=[u0,u1,…,um+k+1]，V=[v0,v1,…,vn+l+1].

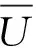
i=(0,1,…,m+1)，j=(0,1,…,n+1).

则新的NURBS曲面表示如下：

(5)

式(5)中(u,v)∈[0,1]×[0,1]， NURBS曲面中在同一位置重复插入同一节点的算法和NURBS曲线的也是一样.

3 细分建模技术设计实现

3.1 整体架构设计

本文选择Visual Studio 2015作为应用程序开发工具， 使用Qt作为图形用户界面应用程序开发框架. 在软件中实现了NURBS细分建模的功能.NURBS曲面三维建模的流程图如图1所示.

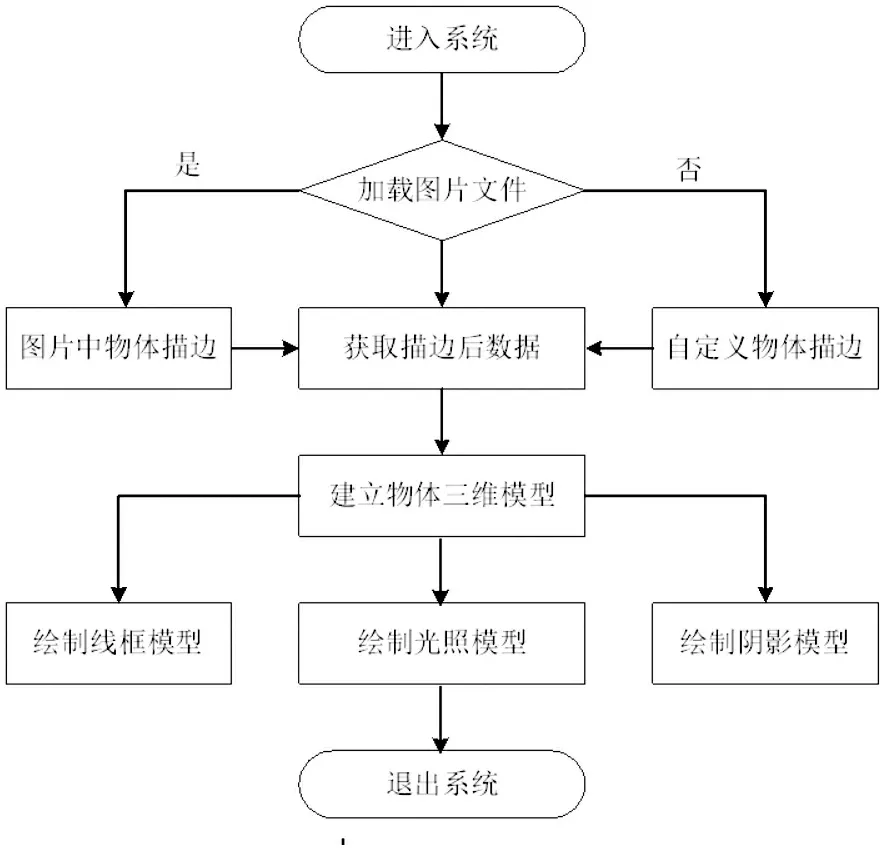
图1 物体建模的流程图

开发的系统主要功能界面如图2所示.

图2NURBS曲面细分建模系统主界面

3.2 模块功能设计

首先加载图片文件， 并对图片中的物体进行描边. 描边完成之后获得描边数据,然后进行细分建模， 加载图片建模的界面如图3所示.

3.3 细分建模的主要算法

令inTime 为细分次数， Vertices为控制顶点， _W为权因子. 节点矢量细分算法、插入节点后计算新顶点算法的伪码如下:

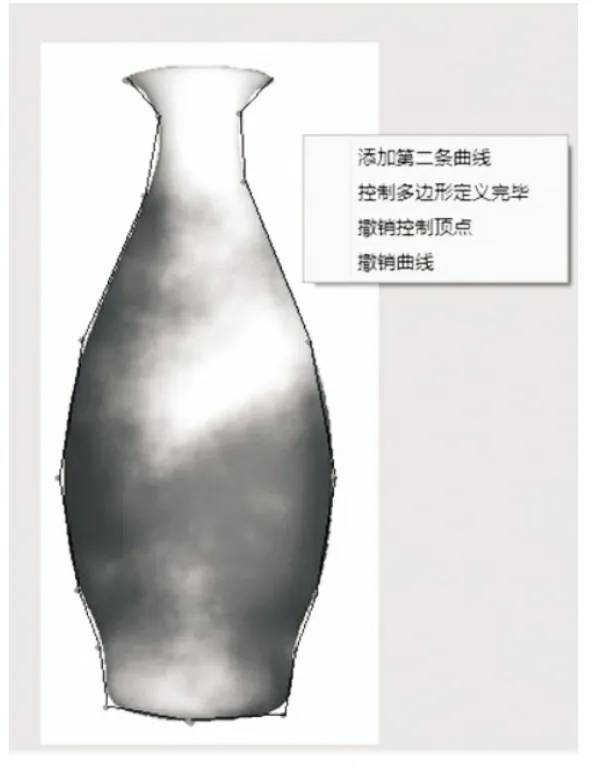
图3 加载图片建模的界面

(1)节点矢量的细分算法

SubdivideCurveKnots

for uTimes←0 to Number of Subdivisions

for indexJ←K to length[Vertices]

node← (Node[indexJ + 1] - Node[indexJ]) / 2.0

insert new node to Node Vector

Sort ,Getting the position of new node in the Node Vector

Generating new vertex data with newNode Vector

(2)节点矢量的细分后计算新顶点的算法

CurveKnotInsertVertex

position←the position of new nodes in the Node Vector

inInsertKnot ← new node value

for j ← position- K + 1 to position+1

numerator←inInsertKnot - Node[j]

denominator←Node[j + K+ 1] - Node[j]

aj← 0.0

if (0 == numerator or 0 == denominator)

aj←0.0

aj←numerator / denominator

Vertices[j]←aj * W[j] * Vertices[j] + (1 - aj) * W[j - 1] * W[j - 1]

W[j] ← aj * W[j] + (1 - aj) * W[j - 1]

Vertices[j] ← Vertices[j] / W[j]

for j ← inIndex + 1 to length[Vertices]

Vertices[j] ←Vertices[j - 1]

W[j] ← W[j - 1]

4 细分建模过程实现效果

正方体细分过程实现的效果如图4～图7所示， 通用物体细分实现的过程效果如图8～图11所示.

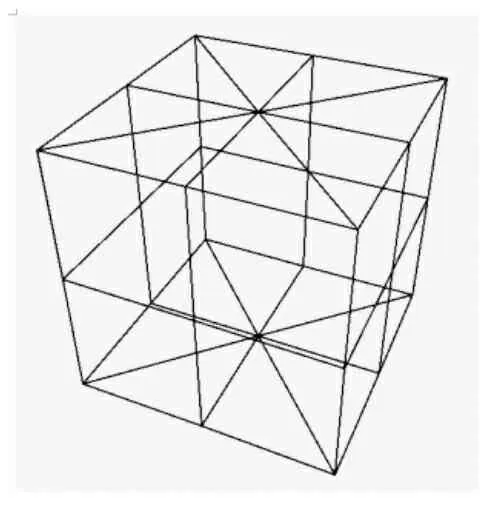
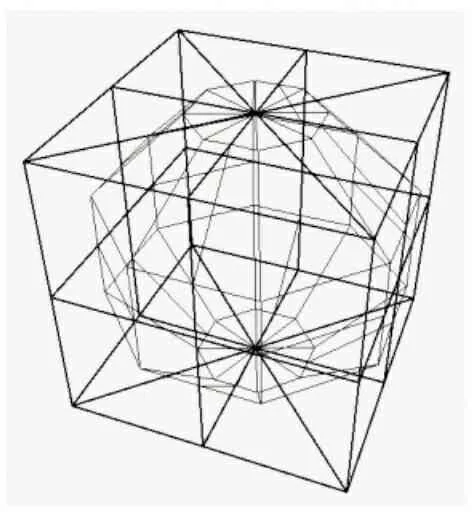
图4 细分零次

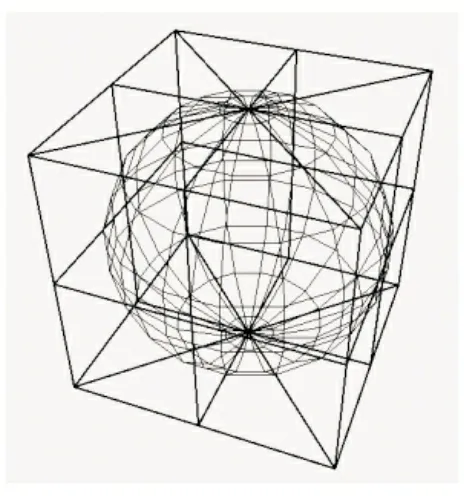
图5 细分一次

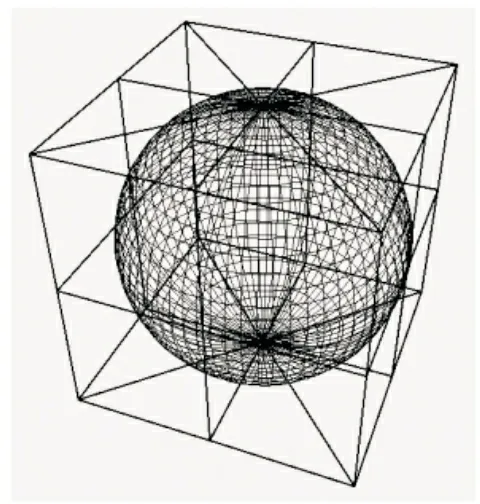
图6 细分二次

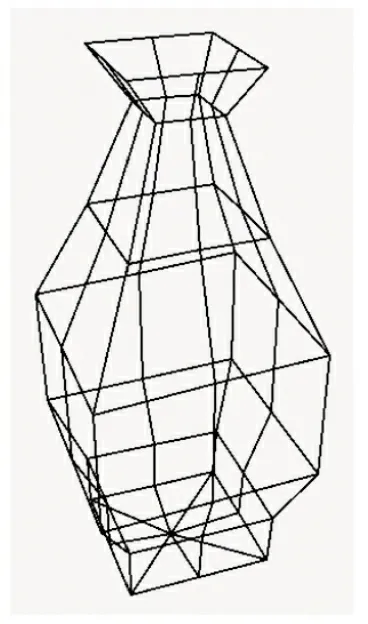
图7 细分四次

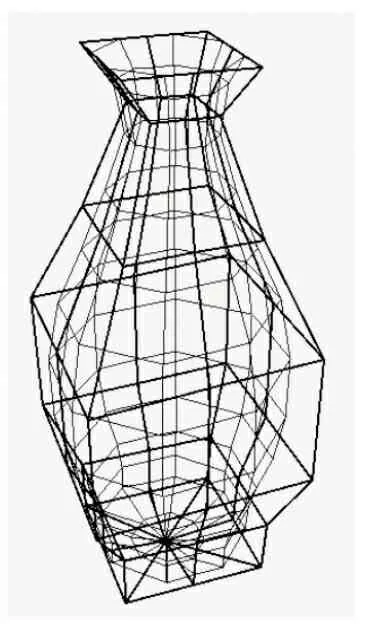
图8 细分零次

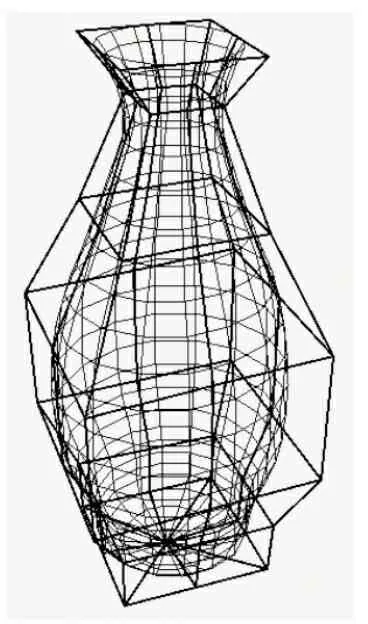
图9 细分一次

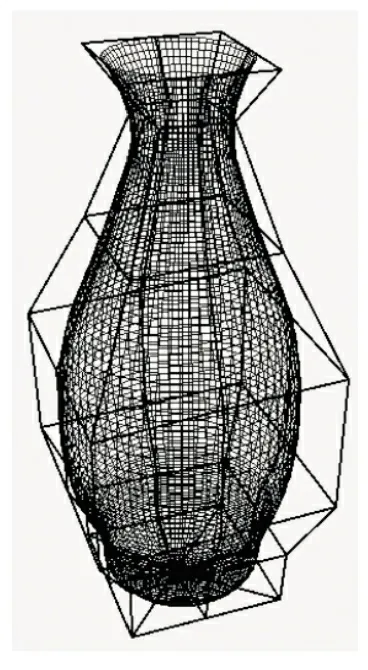
图10 细分二次

图11 细分四次

5 结语

曲面细分能在原始模型顶点数据的基础上， 计算生成多倍的顶点， 新顶点与原始顶点构成的曲面依然保持其几何性质. 与计算机图形学中的纹理映射模拟真实的画面效果不同， 细分的画面效果等同于建模的时候直接设计出来的， 但数据量、处理时间也相对增大. 但是该方法数值计算稳定， 算法简单， 并可部分细分， 与NURBS曲面相比， 它更适合于CG动画和雕刻曲面的设计.