基于分解协调法的梯级泵站优化模型局部敏感性分析
2020-06-11张焱炜李传奇崔佳伟
张焱炜,李传奇,孙 策,崔佳伟
(山东大学土建与水利学院,济南 250061)
0 引 言
我国气候变化复杂,地势、地形南北和东西差异较大,水资源的时空分布不均匀且年际变化大[1]。为优化水资源、解决区域水资源供需矛盾,我国建设了大量的长距离输水工程。梯级泵站作为输水工程的主要动力枢纽之一,对其进行优化调度和敏感性分析的研究,不但能有效提高泵站运行效率、减少泵站运行费用,同时还能确保供、输水的安全稳定和提高输水工程的经济效益[2]。国内外学者对于梯级泵站优化调度进行了较多的研究。郑和震[3]采用动态规划法并基于分时电价规则对梯级泵站输水系统进行了优化调度;梁兴[4]采用混合粒子群算法对梯级泵站建立了优化调度模型。除此之外,包括共轭梯度法[5]、模拟退火法[6]和改进遗传算法[7]等数学算法也被应用到梯级泵站的优化调度研究中。但是,目前对于影响泵站运行的敏感性因素的研究却并不充分,且多局限于单级泵站。曹蓉[8]选取日运行时段划分方式、日均扬程和日提水量作为研究参数,对单级泵站日运行电费优化模型进行了敏感性分析研究。韩典乘[9]对单级泵站优化模型中的瞬时流量、扬程及日调水量等参数进行了敏感性分析。因此,在以上研究基础上对梯级泵站能耗优化模型和电费优化模型开展参数敏感性研究是十分必要的。
本文以南水北调济南市玉符河卧虎山水库梯级泵站为研究对象,基于分解协调法构建了梯级泵站优化调度模型,针对瞬时流量、前池水位、后池水位、日调水量、高峰时段最小流量、低谷时段最大流量等参数,采用修正的Morris筛选法[10,11]进行敏感性分析,从而为梯级泵站优化调度的精确建模和泵站实际运行的敏感性因素探究提供了借鉴和指导意义。
1 模型与方法
梯级泵站的调水量一般通过严格的论证,在相对较短的时期内波动不大,而且各级泵站的过流量是一致的,所以对梯级泵站进行优化调度研究时,很少以优化流量为媒介和研究对象,而是通过优化分配扬程来优化能耗;同级泵站由于各个水泵为并联模式,提水扬程相同,所以同级泵站通过各水泵分配流量的最优化来完成站内优化。本研究以各级泵站站内优化调度模型为基础,通过优化各级泵站的扬程分配构建梯级泵站优化调度模型,并采取动态规划法外加隐枚举法进行求解。以下对模型的建立方法和参数敏感性分析方法进行介绍。
1.1 单级泵站优化模型
在同级泵站里,由于工频泵和变频泵工作方式的不同,因此对两者分别进行优化。工频泵采用枚举法,变频泵采用动态规划法,最后再对总系统进行流量优化分配。
1.1.1 工频泵能耗优化模型
工频泵子系统能耗优化目标函数为总抽水功率最小:
(1)
流量约束条件:
(2)
(3)

1.1.2 变频泵能耗优化模型
变频泵子系统能耗优化目标函数为总抽水功率最小:
(4)
流量约束条件:
(5)
(6)
变频系数约束条件:
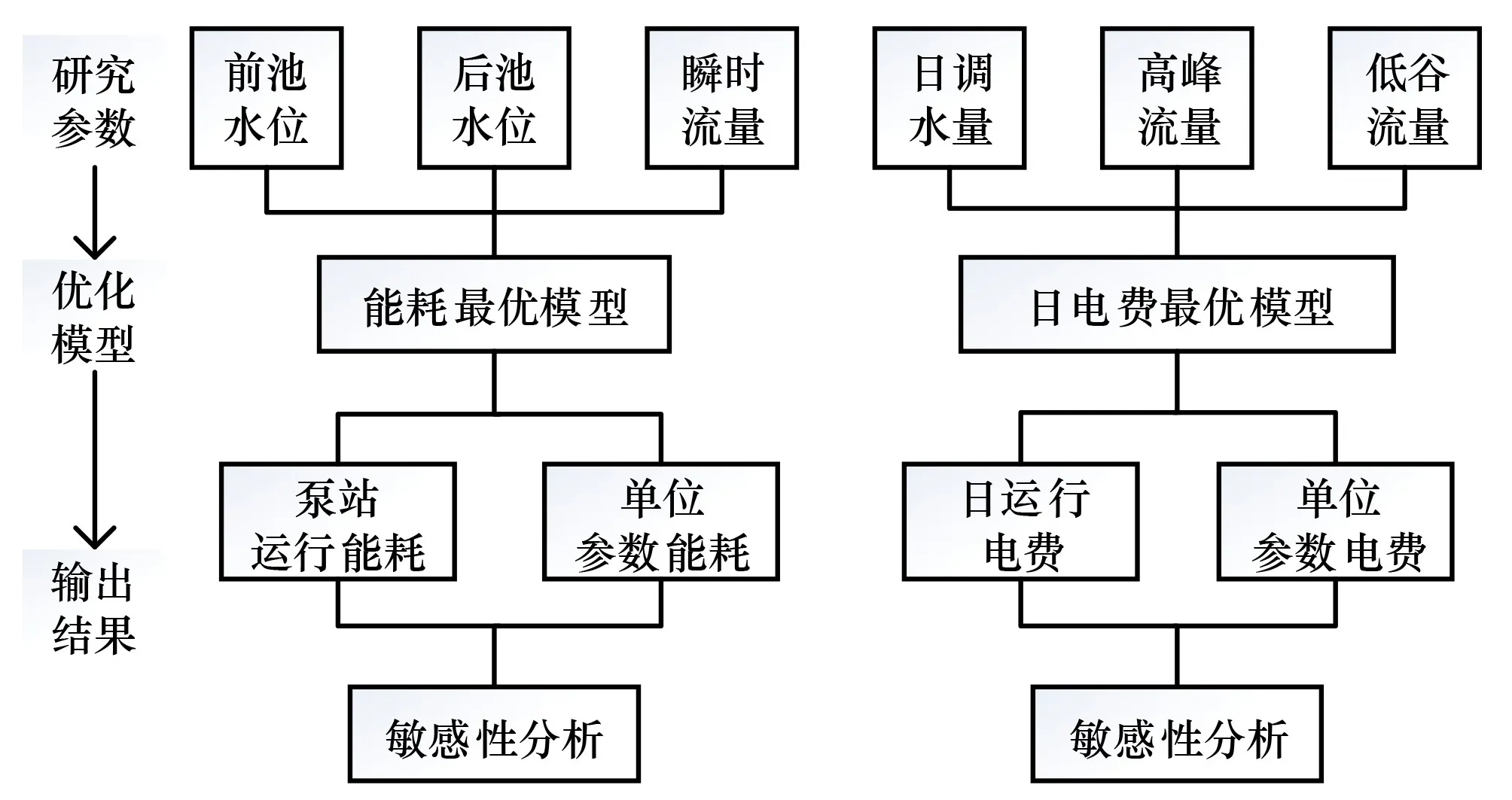
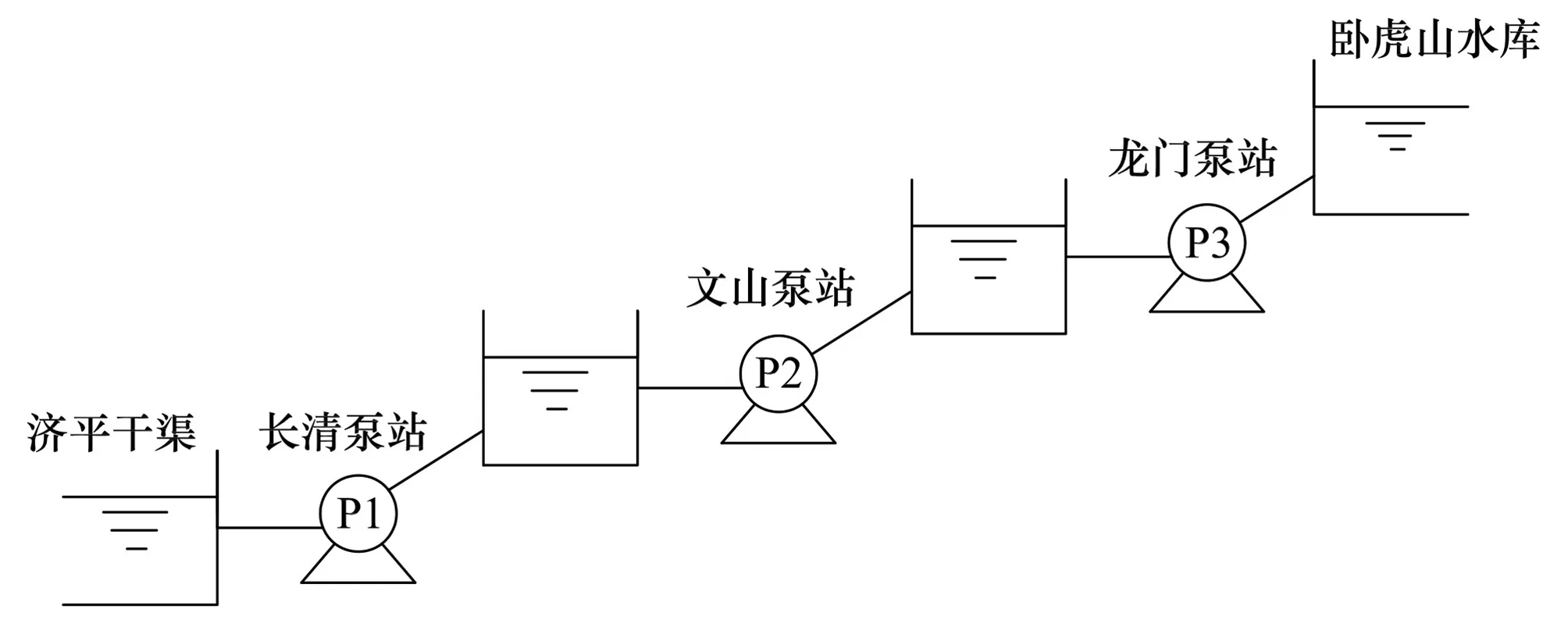
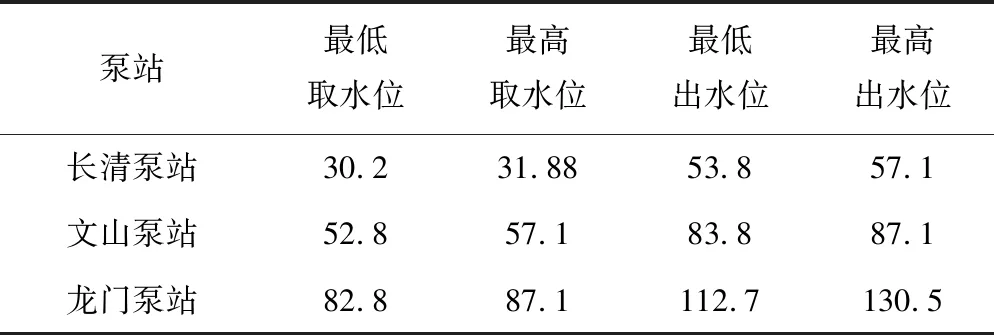
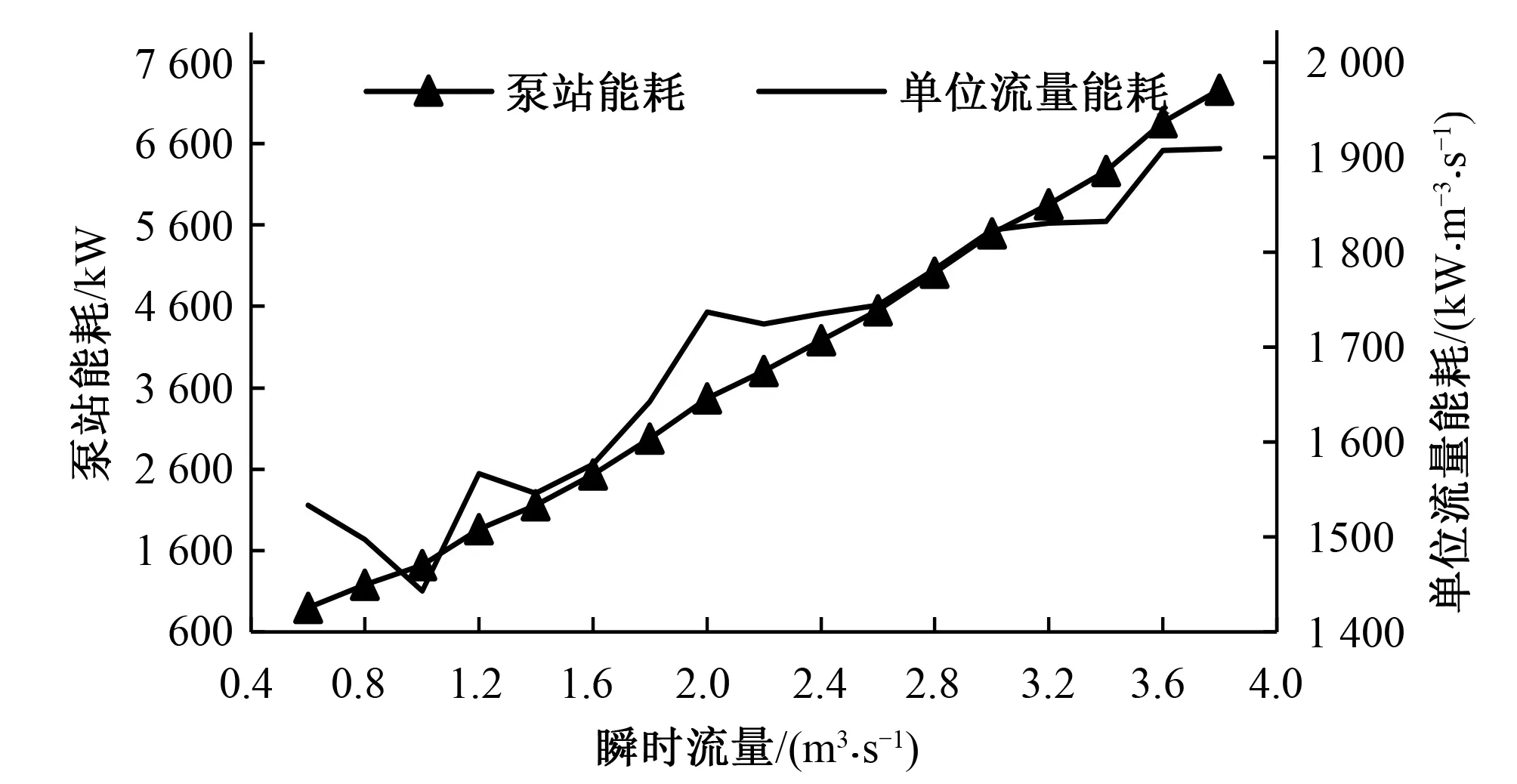
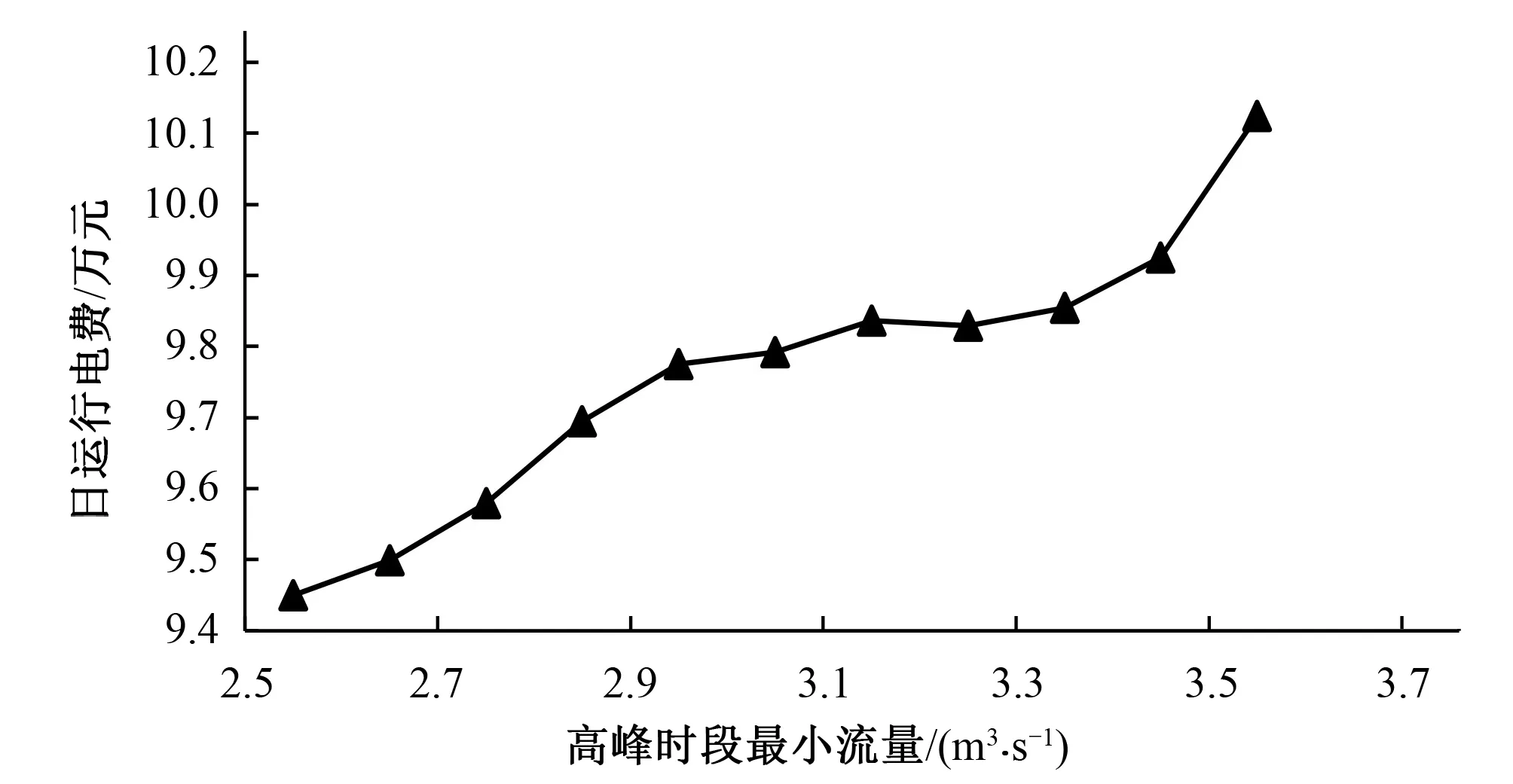
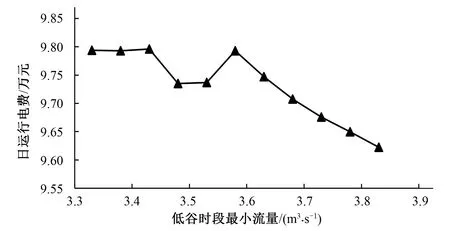
0.6 (7) 1.1.3 总系统优化调度模型 总系统优化模型将总流量在工频泵和变频泵子系统之间进行协调最优分配,使整个泵站的能耗最小。 目标函数: F=min[f1(Qa)+f2(Qb)] (8) 流量约束条件: Qa+Qb=Q (9) 梯级泵站优化调度模型通过调整不同的水位变幅,即不同的进、出水位组合,得到各级泵站不同的扬程组合,再进行站内优化求出该扬程下各级泵站的最小能耗,最后比较出梯级泵站能耗最小的扬程组合。 1.2.1 梯级泵站能耗优化模型 在单级泵站优化模型的基础之上,协调分配各级泵站进、出水位,以达到输水系统能耗最低的目标。 目标函数: (10) 约束条件: (11) 0≤Q≤Qmax (12) 1.2.2 梯级泵站电费优化模型 在梯级泵站能耗优化模型的基础之上,基于分时电价规则,协调分配日均流量,以达到输水系统电费最低的目标。 目标函数: (13) 约束条件: (14) 式中:F为总电价,元;Qi为梯级泵站时段i内的输水流量,m3/s;Ti=1 h;Ci为时段i下的电价,元;p为一天总小时数。 Morris筛选法是一种局部敏感性分析方法,它的原理是选定一个研究参数在其取值范围内不断变化,固定其他参数不变,运行模型得到一系列的输出变量值,最后通过灵敏度判别因子来量化该研究参数对模型输出的影响程度[12]。 ei=(y*-y)/Δi (15) 式中:y为研究参数初始值对应的输出;y*为研究参数改变后对应的输出;Δi为研究参数的变化值。 修正的Morris筛选法是在研究参数的取值范围内选定一个初始值,然后以一个固定的变化百分率步长在取值范围内选取一系列的输入数据,最后根据下式计算研究参数的灵敏度: (16) 式中:SE代表灵敏度判别因子;Y0代表研究参数初始值对应的模型输出值;Yi和Yi+1代表研究参数第i和i+1个取值对应的模型输出值;Pi+1和Pi分别表示研究参数的第i+1和i个取值相对于初始值的变化百分率;n为模型运行次数。 根据数值的大小,可将参数的敏感性分为以下4类[13]:①如果0≤|SE|<0.05,则该研究参数为不敏感参数;②如果0.05≤|SE|<0.2,则该研究参数为中等敏感参数;③如果0.2≤|SE|<1,则该研究参数为敏感参数;④如果|SE|≥1,则该研究参数为高敏感参数。 本文基于梯级泵站能耗优化模型和日电费最优模型,分别选取若干影响参数进行敏感性分析,具体步骤见图1。 图1 敏感性分析步骤图Fig.1 Sensitivity analysis step diagram 玉符河卧虎山水库输水工程属于南水北调东线济南市市区续建配套工程,输水管线自济平干渠贾庄分水闸起,经长清、文山、龙门三级加压泵站提水至卧虎山水库,整条线路总长为29.618 km,输水能力为30 万m3,即3.47 m3/s。图2为梯级泵站输水系统示意图。 图2 泵站输水系统示意图Fig.2 Schematic diagram of the water delivery system 每个加压泵站都配有6台离心泵。其中,长清泵站为6台工频泵(1台备用),文山和龙门泵站各有4台工频泵(1台备用)和2台变频泵。各泵站的进出水位设计指标如表1所示。 表1 泵站进出水位设计指标 m 水泵的流量-扬程-功率特性曲线可以通过拟合得到,根据厂商提供的水泵性能参数和流量、扬程、功率数据,得到以下公式[14]: (17) (18) 式中:H为水泵扬程,m;N为水泵轴功率,kW;R为变频系数。工频泵流量-扬程曲线中最后的常数项,文山泵站取68.41,长清、龙门泵站取70.41;变频泵流量-扬程曲线中最后一项,文山泵站取68.41R2,龙门泵站取70.41R2。 输水管道为铸铁钢管,沿程水头损失采用基于达西公式的舍维列夫公式[15],局部水头损失取沿程水头损失的10%计算[16],将经验公式与泵站设计数据拟合得到管路损失的特性曲线如下: (19) 式中:Hf为单级泵站需要扬程,m;Z1、Z2分别为该级泵站进、出水位,m;Q为瞬时流量,m3/s。 在能耗模型中,选取梯级泵站前池水位(梯级泵站进水水位)、卧虎山水库后池水位(梯级泵站出水水位,以下简称后池水位)和瞬时流量为研究参数;在电费模型中,选取日调水量、电价高峰时段流量和低谷时段流量为研究参数。两个模型参数的取值范围如表2。 表2 各参数取值范围Tab.2 Range of values 3.1.1 前、后池水位敏感性分析 前池水位以31.0 m为初始值,前后变化间隔为0.1 m,各取8个数值,固定梯级泵站后池水位为121.6 m,瞬时流量为设计流量3.47 m3/s;后池水位以121.6 m为初始值,前后变化间隔为1 m,各取8个数值,固定前池水位为31.0 m,瞬时流量为设计流量3.47 m3/s。代入模型计算得到梯级泵站能耗和扬程能耗比(图3、4),并且得到参数的SE值(灵敏度判别因子)。 图3 前池水位-能耗关系Fig.3 Relationship between water consumption and water level of the front pool 图4 后池水位-能耗关系Fig.4 Relationship between water consumption and water level of the back pool 可以看出,①随着前池水位的提高,梯级泵站净扬程降低,泵站能耗降低。能耗扬程比虽然整体上呈减小趋势,但是波动剧烈,原因可能是净扬程的降低导致优化过程中某级泵站的某些单泵关闭、流量增加或者变频系数的变化影响了局部水头损失和单泵的效率。在水位30.8~31.5 m之间,能耗扬程比波动较小,整个泵站运行稳定;②随着后池水位的提高,梯级泵站净扬程增加,泵站能耗增加。能耗扬程比逐渐降低且波动很小,原因可能是模型的优化过程从第一级泵站开始,后池水位的变化对单泵的关闭、流量和效率的影响相对较小,在水位126.6~127.6 m之间,能耗扬程比斜率最小,整个泵站运行最稳定。 同时,根据公式 (16) 计算,前、后池水位的SE值分别为-0.543和0.347,皆为敏感参数。 3.1.2 瞬时流量敏感性分析 瞬时流量以2.2 m3/s为初始值,前后变化间隔为0.2 m3/s,各取8个数值。此时固定前池水位为31.0 m,后池水位为121.6 m,代入模型计算得到梯级泵站能耗和流量能耗比(图5),并且得到参数的SE值。 图5 瞬时流量-能耗关系Fig.5 Relationship between energy consumption and instantaneous flow 由图5可以看出,随着瞬时流量的增加,泵站的能耗基本成线性增加,能耗流量比波动较大,原因是瞬时流量不但影响着梯级泵站的扬程分配和沿程、局部水头损失,同时还影响着单级泵站机组本身的效率、提水扬程和开机台数等,即对于单泵是否在高效区工作、是否关闭和变频系数的变化有直接影响。在设计流量3.47 m3/s附近,能耗流量比基本呈线性状态,泵站运行稳定。 同时,根据公式 (16) 计算,瞬时流量的SE值为1.156,为高敏感参数。 3.2.1 日调水量敏感性分析 日调水量以20.5万m3为初始值,前后变化间隔为1万 m3,各取10个数值,此时固定前池水位为31.0 m,后池水位为121.6 m,峰谷流量不限制,代入模型计算得到调水量变化下的梯级泵站日运行电费和单位提水电费(图6),并且得到参数的SE值。 图6 调水量-日运行电费关系Fig.6 Relationship between daily electricity cost and quantity of water transfer 由图6可以看出,日运行电费随日调水量的提高而增加,单位提水电费虽然整体上处于增加的趋势,但是波动较大,分析原因是:随着日调水量的提高,在能耗中占主要地位的沿程水头损失增大速度高于实际净功的增长速度,同时机组开机台数的增加导致某些时刻局部水头损失增加。在设计调水量29万m3附近,泵站运行稳定。 同时,根据公式 (16) 计算,日调水量的SE值为1.158,为高敏感参数。 3.2.2 峰谷流量敏感性分析 固定前池水位为31.0 m,后池水位为121.6 m,调水量为27.5万m3。取电价高峰阶段最低流量初始值3.05 m3/s,前后变化间隔0.1 m3/s,各取5个数值;取电价低谷阶段最大流量初始值3.58 m3/s,前后变化间隔0.05 m3/s,各取5个数值。代入模型计算得到日优化电费与它们的关系如图7、8,并得到参数的SE值。 图7 高峰时段最小流量-日运行电费关系Fig.7 The relationship between daily electricity cost and minimum flow during peak hours 图8 低谷时段最大流量-日运行电费关系Fig.8 The relationship between daily electricity cost and maximum flow during trough hours 由图7、8可见,高峰时段最小流量越小,日运行电费越低;低谷时段机组运行的最大流量在设计流量3.47 m3/s前后,日运行电费先减少后增加,分析原因可能是分时电价的不等差间隔和单位提水流量的非线性变化的共同作用。 同时,根据式 (16) 计算,高峰时段最小流量的SE值为0.223,为敏感参数;低谷时段最大流量的SE值为-0.144,为中等敏感参数。 本文利用修正的Morris筛选法对梯级泵站能耗优化模型和日运行电费模型进行了敏感性分析,研究了泵站实际运行的特征规律和敏感性因素,得到了以下结论。 (1)修正的Morris筛选法可作为分析梯级泵站优化调度模型参数敏感性的有效方法,为梯级泵站优化调度的精确建模和探究泵站实际运行的敏感性因素提供了借鉴和指导意义。 (2)对于能耗优化模型,参数的敏感性排序为:瞬时流量(1.156)> 前池水位(-0.543)> 后池水位(0.347)。瞬时流量不但影响着水头损失,也对单级泵站的扬程分配和单泵的流量分配、变频系数、机组的开闭起着决定性作用,是能耗优化模型的最敏感参数。同时,梯级泵站的能耗优化模型是从第一级泵站开始的,前池水位的敏感性要大于后池水位。 (3)对于日运行电费优化模型,参数的敏感性排序为:日调水量(1.158)> 高峰时段最小流量(0.223)>低谷时段最大流量(-0.144)。日调水量是影响日运行电费的主要因素。此外,在不超过机组承受能力和满足各种运行条件的情况下,高峰时段最小流量越小和低谷时段最大流量越大,日运行电费相对来说越小。 本文对梯级泵站的优化调度模型进行了局部敏感性分析,并未考虑参数之间的交互作用,参数的选取也只局限于梯级泵站的外部因素,并未选择管道的阻力系数和管径等的泵站内部的特性参数。笔者建议可以进一步对梯级泵站优化调度模型进行全局敏感性分析,并且进一步扩大参数选取类型,更加深入探究泵站优化调度的特征规律和敏感性因素。 □
1.2 梯级泵站优化模型
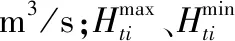
1.3 修正的Morris筛选法
2 研究实例
2.1 水泵的特性曲线
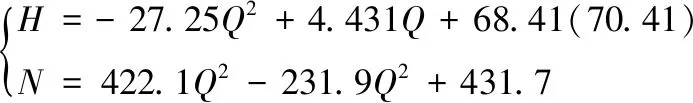

2.2 水头损失
2.3 参数选取
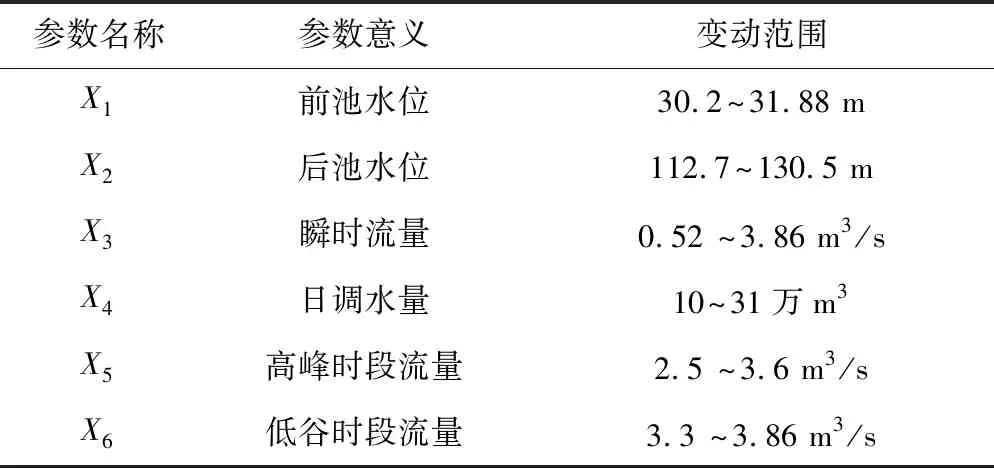
3 结果与分析
3.1 能耗模型敏感性分析
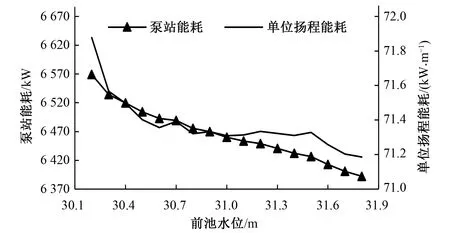
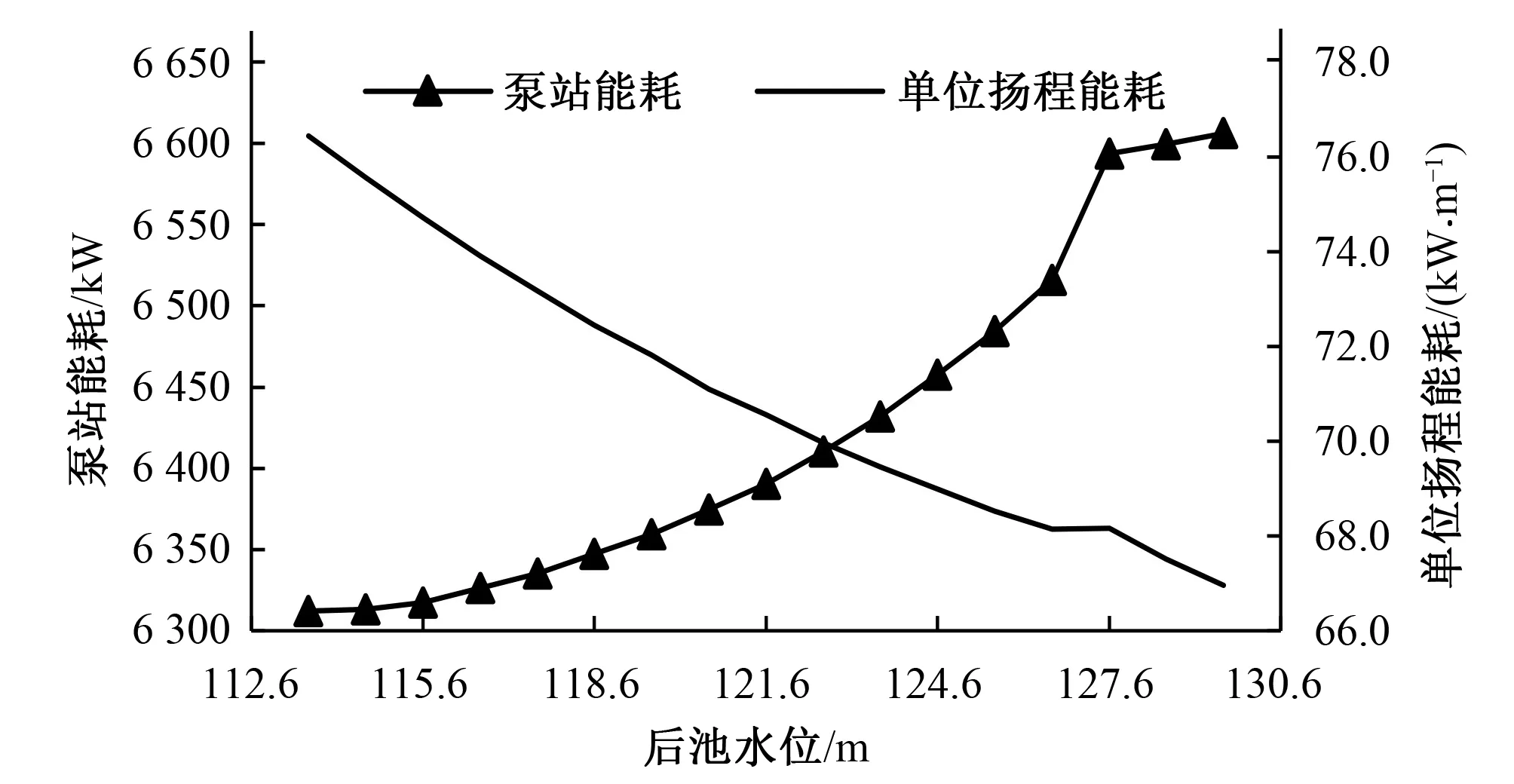
3.2 电费模型敏感性分析

4 结论与建议
