悬链线形断面正常水深与临界水深的直接计算

何 育 聪

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

0 前 言

悬链线形断面不仅在施工、制模过程中易于计算和控制，还具有防止土基冻胀破坏、抵抗外水压力、受力条件好、输砂率高、过水能力强及抵抗冲刷性能好等优点[1,2]，因此，悬链线形渠道近年来在水利发电、灌溉排水和城市给排水工程中得到越来越广泛的应用。

水力计算中的正常水深和临界水深在工程设计中十分重要，应用频繁且有较高的精度要求。近年来，对于几何形状简单的断面如圆形、抛物线形断面的水力计算，国内外已有学者做出了大量研究，提出了不少的简便算法[3-7]，在实际工程问题的解决过程中起到了很大的作用。悬链线形断面正常水深和临界水深的求解涉及高次隐函数方程，没有解析解，求解困难，而且目前关于悬链线形断面正常水深与临界水深计算的研究较少。对于悬链线形断面正常水深的计算方法有：滕凯，文辉，许晓阳[8-10]提出的直接计算式，黄开路[11]提出的迭代计算法;对于悬链线形断面临界水深的计算方法有：滕凯，陈诚，徐军辉[12-15]提出的直接计算式。但这些公式都存在这使用范围受限或精度不高的问题。鉴此，本文基于悬链线形断面几何特点，结合均匀流和临界流基本方程，通过构造牛顿迭代公式和迭代初值公式，提出了一种悬链线形断面水力计算的直接算法。最后通过实例验证了计算方法的合理性。该计算方法不仅具有精度高、适用范围大的特点；还可以为程序提供高精度、快收敛的迭代算法。

1 基本公式

1.1 悬链线形断面的几何特征及水力要素

悬链线形过水断面如图1所示，悬链线形断面的曲线方程为：

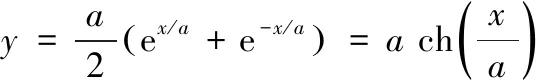
(1)

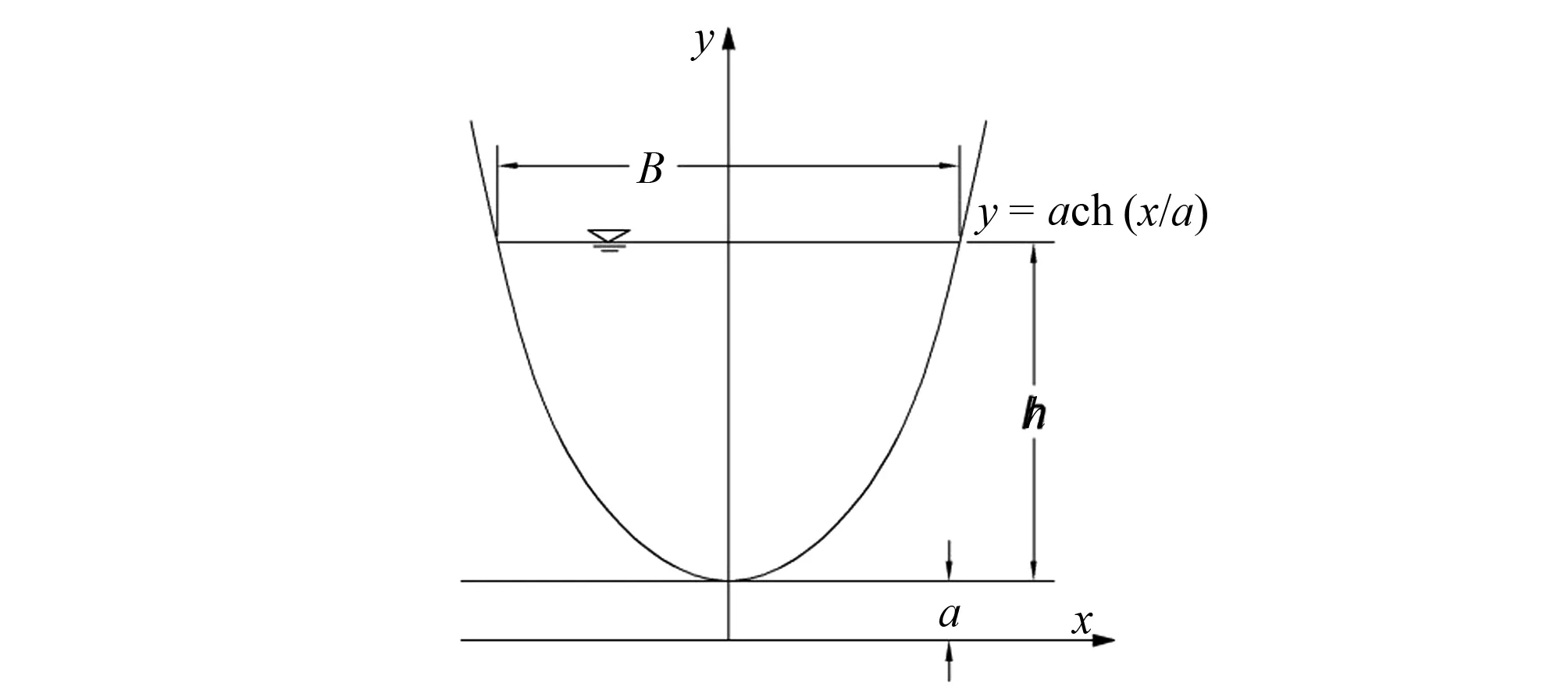
图1 悬链线形过水断面Fig.1 Catenary-shaped cross section

过水断面水力要素为：

(2)

(3)

(4)

式中：χ为湿周，m；A为过水断面面积，m2；a为悬链线形断面形状参数(a>0)，m；B为水面宽度，m；x、y为曲线上任一点的横纵坐标，m。

由式(2)、式(3)、式(4)可得：

(5)

(6)

(7)

1.2 悬链线形断面均匀流和临界流方程

根据《水力学》[16]知，均匀流基本方程为：

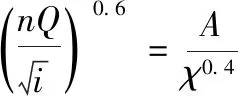
(8)

临界流基本方程

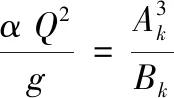
(9)

式中：Q为渠道流量，m3/s；n为渠道糙率系数；i为渠道设计坡降；A为过水断面面积,m2；χ为湿周，m；α为流速分布不均匀系数；g为重力加速度，取9.81 m/s2；Ak、Bk分别为临界流过水断面面积和水面宽度。

将式(6)、(7)带入式(8)，整理可得：

(10)

将式(5)、式(7)代入式(9)，整理可得：

(11)

为方便分析，令：

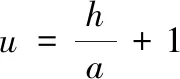
(12)

(13)

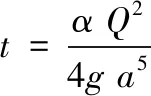
(14)

式中：u为无量纲水深；k，t为无量纲参数。已知数学变换：

(15)

将式(12)、式(13)、式(15)带入式(10)，整理可得悬链线形断面均匀流方程：

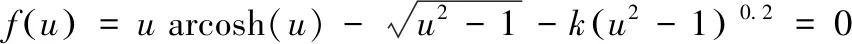
(16)

将式(12)、式(14)、式(15)带入式(11)，整理可得悬链线形断面临界流方程：

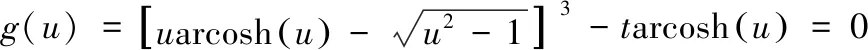
(17)

悬链线形断面正常水深和临界水深的求解问题即为式(16)、式(17)的求根问题。利用已知的n,Q,i,a可以求出k、t。将k、t分别代入式(16)、式(17)，并分别求根u,最后根据式(12)可以求得正常水深和临界水深。

2 a值的确定

在设计悬链线形断面时，通常只给出设计流量下对应正常水深的水面宽度B和a的比值η=B/a，而不直接给出a的值。

将式(2)、式(3)带入式(8)，整理得：

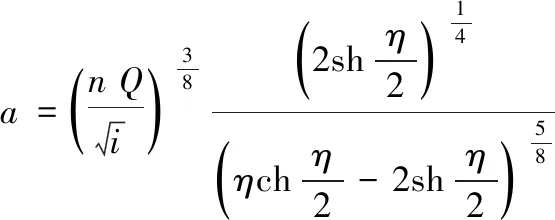
(18)

由式(18)可直接求得a的值，然后将a和η代入式(4)可以直接求出设计流量下正常水深h的值，即：

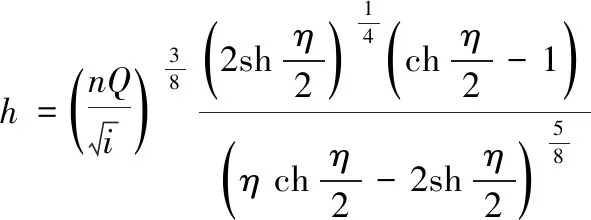
(19)

3 悬链线形断面正常水深的直接计算公式

3.1 正常水深的牛顿迭代式

悬链线形断面正常水深的求解问题就是非线性方程(16)的求根问题，对式(16)进行数学变换得到悬链线形断面正常水深的牛顿迭代公式：

(20)

由式(20)迭代计算出无量纲正常水深u之后，将u代入式(12)即可求得正常水深。

3.2 u的取值范围及合理迭代初值选择

悬链线形断面的水力最佳断面的条件[2]是B/a=3.21223,将其代入式(4)可求得h/a=1.5921。以h/a=1.5921为中心，扩展其取值范围为[h/17a,17h/a]=[0.093 65,27.065 7],取[0.09,29.00]作为h/a的取值范围，即u∈[1.09,30.00]作为本文正常水深直接计算公式的适用范围。

迭代计算的精度与收敛速度不但和迭代公式的形式有关，还与迭代初值的选取有关。只有选取合适的迭代初值，才能有高的计算精度和快的收敛速度。运用MATLAB，采用合适的函数模型，对千余组散点(k、u)进行拟合分析，使拟合公式的相关系数最大，得到如下拟合公式：

u=1.087k0.741 1+0.230 8k1.367+0.995 9

(21)

将式(21)代入式(20)，只进行一次迭代计算便得到正常水深的直接计算式：

(22)

式中：u=1.087k0.741 1+0.230 8k1.367+0.995 9。

4 悬链线形断面临界水深的直接计算公式

4.1 临界水深的牛顿迭代式

悬链线形断面临界水深的求解问题就是非线性方程(17)的求根问题，对式(17)进行数学变换得到悬链线形断面临界水深的牛顿迭代公式：

uj+1=

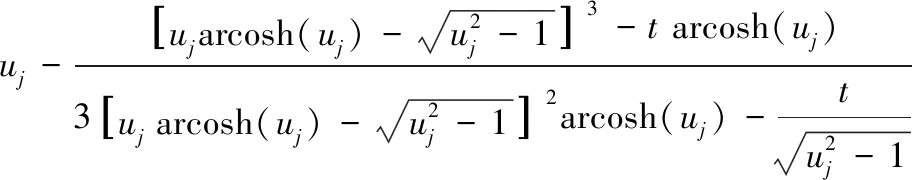
(23)

4.2 u的取值范围及合理迭代初值选择

由文献[13]可知，实际工程中无量纲临界水深hk/a的取值范围不会超出[0.537, 6.945]，即u不会超出[1.537, 7.945],本文扩大其范围取a∈[1.5,10.0]。

运用MATLAB，采用合适的函数模型，对千余组散点(k、u)进行拟合分析，使拟合公式的相关系数最大，得到如下拟合公式：

u=1.053t0.240 9+0.113 7t0.360 9+0.993 2

(24)

将式(24)为代入式(23)，只进行一次迭代计算便得到临界水深的直接计算式：

(25)

式中：u=1.053t0.240 9+0.113 7t0.360 9+0.993 2。

5 精度评价

5.1 公式的误差分析

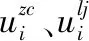
(28)

(29)

编程分别得到无量纲正常水深和临界水深的初值公式和直接计算式的相对误差分布曲线图如图2～图5所示。

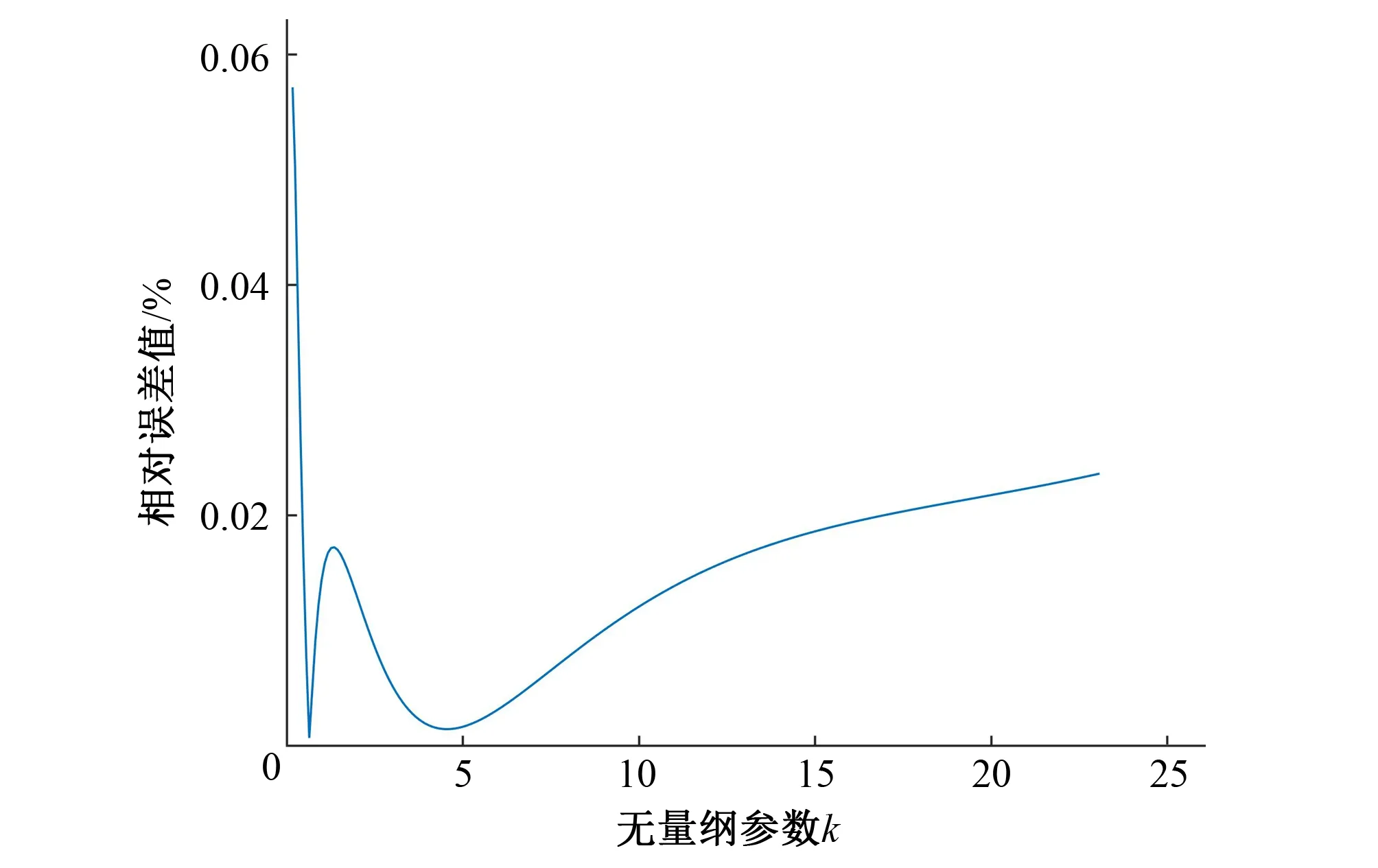
图2 无量纲正常水深初值误差分析Fig.2 initial value error analysis of dimensionless normal water depth

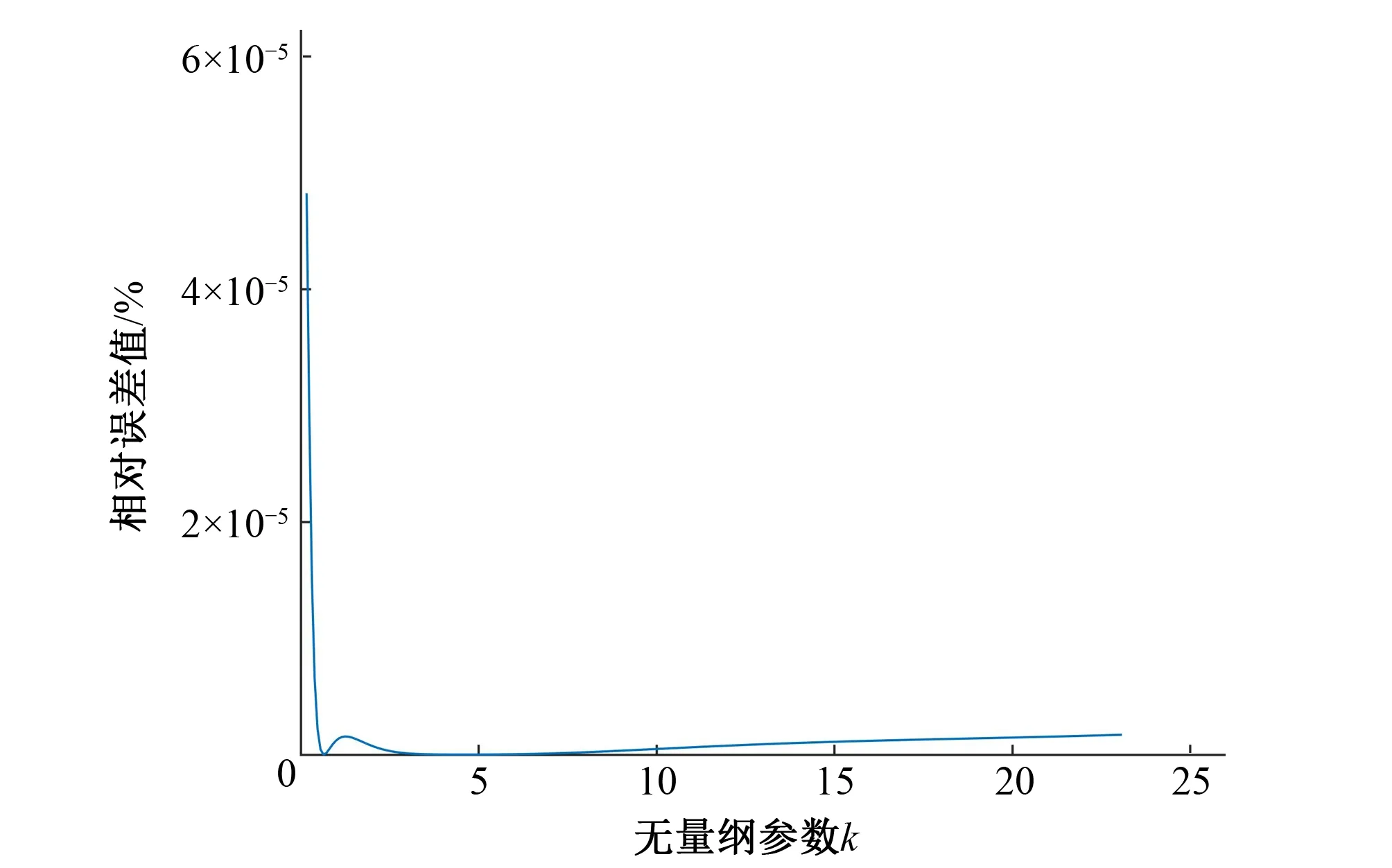
图3 无量纲正常水深误差分析Fig.3 dimensionless normal depth error analysis

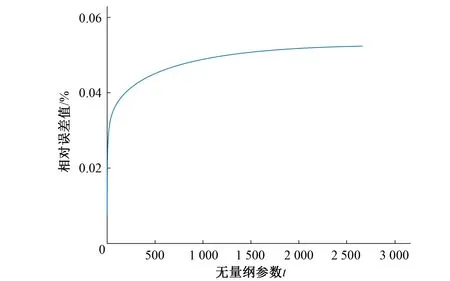
图4 无量纲临界水深初值误差分析Fig.4 error analysis of initial dimensionless critical water depth

对于本文的正常水深直接计算公式来说，初值公式的最大相对误差为0.057 2%，一次迭代后最大相对误差为5.33×10-5%；从图(3)可以看出，当u∈[1.8,30.0]时，最大相对误差为1.78×10-6%。二次迭代后最大相对误差可以减小到1.01×10-13%，精度比一次迭代提高了108倍。

对于本文的临界水深直接计算公式来说，初值公式的最大相对误差为0.052 3%，迭代一次后最大相对误差为5.05×10-5%。二次迭代后最大相对误差减小到4.71×10-11%，精度比一次迭代提高了106。

本文的悬链线形断面正常水深和临界水深公式的精度均远高于工程要求。

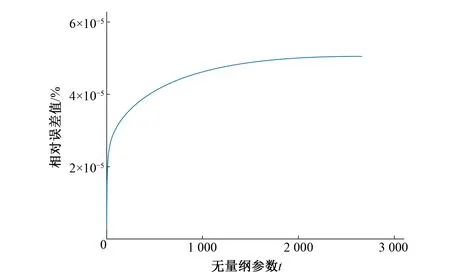
图5 无量纲临界水深误差分析Fig.5 Dimensionless critical depth error analysis

5.2 与前人公式对比

现将已有的悬链线形断面正常水深及临界水深直接计算公式进行统计，并将这些公式用统一的参数表示，结果如表1，表2。

6 应用举例

选择文献[17]算例：某断面形状为悬链线形的渠道，其设计流量Q=3 m3/s，渠道坡降i=1/1 500，糙率n=0.014，η=3.315。

在工程设计中，设计流量可以直接求得正常水深的精确值；再用本文公式计算正常水深，从而对公式的精度进行验证。临界水深的精确值则通过编程迭代运算得到：

表1 悬链线形断面正常水深计算公式统计表Tab.1 Statistics table of calculation formulas for normal water depth of catenary linear section

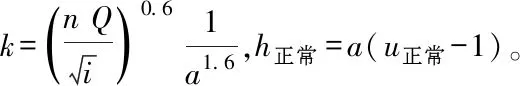
(1)正常水深精确值：将η、n、i、Q代入式(20)、式(21)，求得a=0.761 900 371 837 558,正常水深精确值h1=1.309 247 279 446 131。

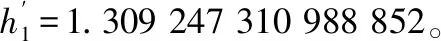
(3)临界水深精确值：利用迭代式(25)进行编程，取g=9.81 m/s2。使得u的最后两次迭代值的误差小于10-15，得到u2=2.127 411 917 909 701，代入式(14)计算得到h2= 0.858 975 559 469 495。

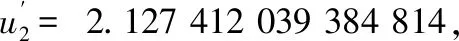
7 结 论

结合悬链线形断面几何特征、水力要素和临界流、均匀流其中t=αQ2/(4ga5)，h临界=a(u临界-1)。

表2 悬链线形断面临界水深计算公式统计表Tab.2 Statistical formula for calculating critical water depth of catenary linear section

基本方程，得到了悬链线形断面临界流与均匀流方程。通过引入合适的无量纲参数，对临界流和均匀流方程进行数学变换，得到临界水深和正常水深的牛顿迭代式，再利用优化拟合原理得到临界水深和正常水深的初值计算公式，一次迭代后得到正常水深和临界水深的直接计算公式。最后对公式进行误差分析及比较，表明在工程适用范围内：无量纲正常水深的初值计算公式最大相对误差绝对值为0.057 2%，直接计算公式最大相对误差绝对值为5.33×10-5%；无量纲临界水深初值计算公式的最大相对误差绝对值为0.052 3%，直接计算公式的最大相对误差绝对值为5.05×10-5%，远高于现有计算公式精度，且公式适用范围广、物理概念清晰，可以应用于软件算法。

□