考虑动态导向与邻域交互的双蚁型算法*

潘 晗，游晓明，刘 升

1.上海工程技术大学 电子电气工程学院，上海201620

2.上海工程技术大学 管理学院，上海201620

1 引言

旅行商问题（traveling salesman problem，TSP）是一个经典的组合优化问题，也是图论中最著名的问题之一。该问题可以这样描述：假如一个旅行商必须经过N个城市，无论选择什么样的路径，都不能重复经过每一个城市，最终还需要回到开始出发的城市。路径选择的要求是使得旅行商经过N个城市的路径之和最小。由于TSP 问题又是一个NP 完全问题，解决方法主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

蚂蚁在行动的过程中会释放一种特殊的信息素，由于信息素的累加，可以改变蚂蚁的行动方向。根据这种信息传递机制，蚂蚁能够更快地往返于食物源和巢穴之间，从而更有效地运送食物。20 世纪90 年代，意大利学者Dorigo 等人通过观察蚁群觅食的过程和不断的研究，首先提出来一种新的群智能算法——蚁群算法，此方法被成功地应用到了求解旅行商问题和二次分配问题中。最初的蚁群算法是蚂蚁系统（ant system，AS）[1]，蚂蚁系统有三种基本模型，分别是蚁周模型（ant cycle）、蚁密模型（ant density）、蚁量模型（ant quantity）。但是由于蚂蚁系统工作过程中间的停滞问题，易于陷入局部最优的解和较长搜索时间的问题。1997 年，Dorigo 等人在蚂蚁系统的基础之上又提出了蚁群系统（ant colony system，ACS）[2],它引入了全局更新的概念，创建路径的过程中所使用的状态转移规则也优于蚂蚁系统，使得ACS在解决规模较大的TSP 问题时会得到更优解。1997年，Stützle 等人在对蚂蚁系统的实验分析以及应用研究中，提出了最大-最小蚂蚁系统（max-min ant system，MMAS）[3]。MMAS 在每次迭代中只允许表现最好的蚂蚁更新路径上的信息素，并且限定信息素浓度允许值的上下限，其目的是为了防止算法过早停滞，增加算法的多样性。此后，不断地有专家学者在上述算法的基础上进行改进，并成功应用到各种领域[4-11]。

文献[12]将拥挤因子运用到蚁群算法的状态转移和信息素更新过程中。文献[13]使用了一种改进信息素二次更新与局部优化策略，实验结果证明这些算法增强了全局搜索能力，多样性更好，但是收敛速度却有待提高。针对这一不足，文献[14]提出了一种基于最小生成树的改进蚁群算法，将最小生成树的信息加入到路径寻优中来引导蚂蚁的搜索过程，从而加快收敛速度。文献[15]提出将最小生成树的信息加入到启发式信息中来引导蚂蚁的搜索过程。文献[16]是根据最小生成树上的边修改信息素初始值来发挥生成树在路径寻优中的作用。但是上述算法虽然加快了收敛速度，但容易陷入局部最优使其解的精度不够高。针对这一不足，文献[17]将蚂蚁分成若干子群，并引入了吸引因子和排斥因子，实现了一种多蚁群并行选择策略，以加强其全局搜索能力和加快收敛速度。文献[18]运用了正、负反馈机制，利用吸引信息素和排斥信息素来增强蚂蚁之间的交流，加快了算法发现最优解的速度与能力。文献[19]引入了随机进化因子和进化漂变阈值，不仅加快了收敛速度也增强了跳出局部最优的概率，但是上述算法在平衡种群多样性和算法的收敛速度上有待进一步提高。

为了达到种群多样性和算法收敛性的平衡，本文在ACS 的基础上提出了考虑动态导向与邻域交互的双蚁型算法。首先在算法中结合动态导向策略，在迭代前期增加属于最大生成树路径上的动态信息素，以防止概率转移公式中城市之间的距离启发信息占主导地位，使得算法在前期的多样性有很大的提高；因为最小生成树与最优路径之间有着很大的关联，两者之间共同的边高达70%～80%[20]，所以在迭代后期增加属于最小生成树路径上的动态信息素，从而达到加快收敛速度的目的，并提高解的质量。同时加入MMAS 中的信息素限定规则，以避免算法陷入停滞状态。最后结合邻域交互策略，将蚂蚁分成两类，第二类蚂蚁在状态转移和局部信息素更新过程中引入吸引因子，触发了正反馈机制，进一步提高算法的收敛性。仿真结果表明，本文算法既增加了种群的多样性，又加速了算法的收敛速度。

2 相关工作

2.1 ACS 蚁群算法原理

2.1.1 路径构建

为了进一步解决AS 中展现出来的缺陷，提出以Ant-Q 为基础的优化算法——ACS。在ACS 算法中，根据伪随机比例规则，位于第k个城市的第i只蚂蚁选择下一个访问的城市j。这个规则如式（1）：

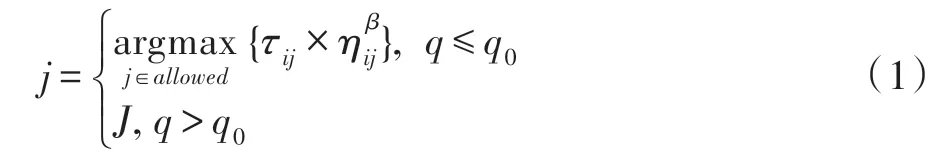
其中，q是均匀分布在区间[0,1]中的一个随机变量，q0（0 ≤q0≤1）是一个参数，ηij表示i、j城市之间距离的倒数，τij表示i、j城市之间信息素的总量，allowed表示不在蚂蚁禁忌表中的城市集合。J是一个随机变量，如式（2）所示：

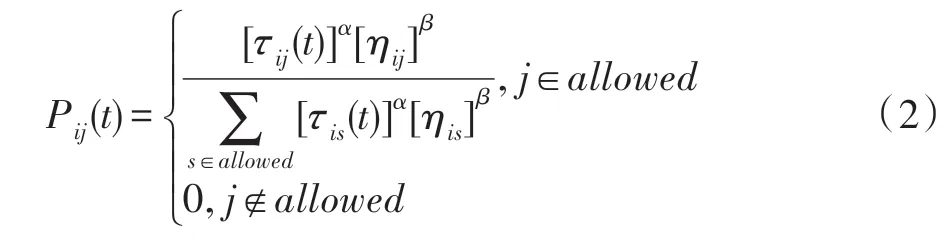
式中，α、β分别表示信息素和启发因子在概率计算中所占的权重。

2.1.2 信息素的更新

（1）全局信息素更新

针对当前最好路径上的边进行信息素更新，更新的规则如式（3）所示：

其中，Δτij=1/Lgb，Lgb代表至今最优路径长度，Δτij表示信息素的增加量，ρ代表全局信息素蒸发速率。全局信息素的更新有助于提高算法的收敛速度。

（2）局部信息素更新

当蚂蚁k从城市i经过下一个城市j之后，i、j城市之间路径上的信息素的更新规则如式（4）所示：

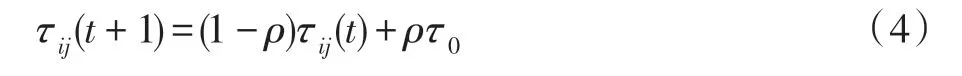
其中，ρ代表局部信息素蒸发速率，τ0代表每条边信息素的初始值。局部信息素的更新使得每条边上的信息素相应地减少，防止算法过早陷入局部最优，增加了算法的多样性。

2.2 MMAS 蚁群算法

为了使得算法在最短路径附近搜索，从而逐步找到全局最优解，算法只会对当前循环中所产生的最短路径进行信息素的更新操作，如式（5）所示：

为了防止某些边上的信息素增长过快，而导致停滞现象的出现，MMAS 算法中任何一条边上的信息素的大小都被限制在[τmin,τmax]的范围内。如果当前边上的信息素的浓度高于τmax时，就使该边上的信息素的浓度定为τmax，τmax如下公式所示：

其中，f(sopt)是全局最优解，ρ是信息素的挥发因子。

如果当前边上的信息素的浓度低于τmin时，就让该边上的信息素的浓度定为τmin，τmin如下公式所示：

其中，pbest是MMAS 算法收敛时找到最优解的概率（一般为0.05）。

2.3 最大最小生成树

最大最小生成树的概念被提出于数据结构中，它们都是树形结构。后来很多专家学者对最大最小生成树算法进行了改进与应用[21-22]。

2.3.1 最大最小生成树的定义

在一个给定的n个顶点的完全连通图G=(V,E)中，顶点u与顶点v的连线的边表示为(u,v)，而w(u,v)代表此边的权重，如果存在T为E的子集且为无循环图，使得w(T)最小，则此T为G的最小生成树，反之如果w(T)最大，则此T为G的最大生成树。w(T)如式（8）所示：

2.3.2 最大最小生成树的构建

最大最小生成树的构造有很多著名的方法，比如克鲁斯卡尔算法（Kruskal）和普里姆算法（Prim）。

（1）Kruskal算法主要思想

将V的每个节点定义为一棵树，并定义为根节点，将E中的边按权重从小到大依次处理。首先判断边的两个节点是否属于同一棵树（根据根节点是否一致），若不是，则合并两棵树，并更新根节点；若是，则不予理会。

（2）Prim 算法主要思想

给定连通图G和任意根节点r，最小生成树从节点r开始，一直长大到覆盖V中所有节点为止，即不断寻找轻量级边以实现最小权重和。

3 改进的蚁群算法

3.1 动态导向策略

在求解TSP 问题中，最小生成树与最优路径之间有着非常密切的关系。在通常情况下，最小生成树中的70%～80%的路径与TSP 问题的最优路径是吻合的。将最小生成树的信息结合到求解TSP 问题中去，且每次迭代，结合的信息素动态变化，使得在求解过程中加快算法的收敛速度，起到了动态正导向性。

TSP 问题里，蚂蚁选择下一个城市的依据有两个因素：一个是i、j城市之间的信息素的浓度启发信息；另一个是i城市到j城市的距离启发信息；即i、j城市之间距离的倒数。城市之间初始信息素为一个常数，在算法首次迭代的时候，每条路径中的信息素对蚂蚁的吸引力都是相同的，而城市之间的距离启发信息是不同的，因此在算法刚开始运行的时候，蚂蚁选择下一个城市的概率是城市之间的距离启发信息占主导地位，即城市之间的距离越短，该路径被选择的概率就越大。但是这条路径所在的解并不一定是最优解，因此容易陷入局部最优解。为了避免这一缺陷，在算法的初期会动态强化最大生成树n-1（n为城市数）条边的信息素，以增加算法的多样性，起到了动态负导向性。

3.1.1 最大生成树策略

属于最大最小生成树边的路径上所释放的信息素称为生成树信息素。在算法的前期，结合最大生成树的信息，在迭代次数n∈(0,n0]时，属于最大生成树中的边的两个城市之间的路径上释放相应浓度的动态信息素，额外增加信息素的量如式（9）所示：

其中，N为最大迭代次数，τ0表示边的信息素的初始值，ρ大表示最大生成树调整因子，以调整生成树信息素在算法前期的影响权重。在多次实验结果的对比下，n0取[N/2]，ρ大取2 的时候，本文实验结果最佳。由于(N-n)/N是减函数，值域在[1/2,1)，因此τ树大也是减函数，添加属于最大生成树路径上的信息素浓度是逐代递减的，即每次迭代在最大生成树的n-1 条边上动态强化的幅度是递减的，使得相应路径的生成树信息素浓度总体增加的同时不会过度累积，以增加算法在前期的多样性，并且前期多样性越来越好，以防止算法陷入局部最优。

3.1.2 最小生成树策略

在算法的后期，结合最小生成树的信息，在当前迭代次数n∈(n1,N]时，属于最小生成树的边的两个城市之间的路径上释放相应浓度的动态信息素，额外增加的信息素的量如式（10）所示：

其中，ρ小表示最小生成树调整因子，用来调整生成树信息素在算法后期的影响权重。本文实验中n1取N-[N/2]，ρ小取2。由于n/N是增函数，值域在（1/2,1]，因此τ树小也是增函数，使得算法后期达到快速收敛的效果。

3.2 邻域交互策略

在初始阶段，将蚁群分成两类种群，两类种群内的蚂蚁释放自己种群内的信息素，使得两类种群蚂蚁工作时有相应的独立性。但是，在第一类蚂蚁按照自己的规则遍历城市的基础上，第二类蚂蚁在选择路径和信息素更新时，会受到第一类蚂蚁在邻域内所释放信息素的影响，即引入吸引因子，使得第二类蚂蚁尽可能容易地选择第一类蚂蚁已经选择过的最优解的部分路径，以达到更快地寻得最佳路径，从而提高了算法整体的收敛速度，使得两个种群有着紧密的交互性。

3.2.1 吸引因子

在第二类蚂蚁遍历城市的过程中，引入吸引因子：

每个以i为圆心的邻域内路径上由第二类蚂蚁释放的信息素的总和是一定的，当第一类蚂蚁在(i,j)城市之间的路径上所释放的信息素越大时，所求的吸引因子的值越大，说明第二类蚂蚁就会以更高的概率选择第一类蚂蚁集中选择过的路径，使得第二类蚂蚁选择城市更具有导向性。

由于吸引因子记录了第一类蚂蚁在路径上释放的相关信息素的信息，在第二类蚂蚁遍历城市时，引入吸引因子，使得第二类蚂蚁在路径选择的时候会考虑到第一类蚂蚁遍历城市时的有关信息。

首先将吸引因子引入到状态转移规则中，如3.2.3 小节的叙述，在综合考虑了第二类蚂蚁自身相关启发信息的同时，还结合了第一类蚂蚁的信息素启发信息，使得第二类蚂蚁选择路径时会受到第一类蚂蚁留下的信息素启发信息的影响，且第一类蚂蚁遍历城市时所选择的较优路径在对第二类蚂蚁选择路径时有更大的影响，体现了第一类蚂蚁的信息素启发信息对第二类蚂蚁的正反馈作用，即吸引因子的正反馈作用。由于正反馈的作用，使得那些较优路径上的信息素累积比一般路径上要快且多，因此算法的收敛速度会加快，并且收敛精度也会提高。

其次将吸引因子引入到局部信息素更新策略中，如3.2.4 小节的叙述，让每条路径的信息素挥发量相应地减少，不仅起到了正反馈作用，同时也抑制了多样性，使得算法的收敛能力得到加强。

综合而言，吸引因子对算法起到了正反馈作用，同时加快了算法的收敛速度，提高了算法的收敛精度。

3.2.2 关联邻域

为了能够高效地结合有效信息素，并且在一定程度上减少每次计算吸引因子的速度，提出了关联邻域的概念，经过多次实验结果分析得出关联邻域的定义如下：

以城市i为圆心，以半径r画一个圆，此圆就称为i城市的关联邻域[23]。半径r的大小如式（12）所示：

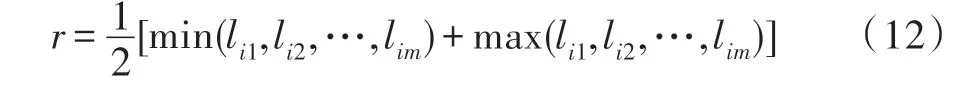
其中，m表示总的城市个数，lim表示第i个城市到第m个城市的距离。

由于本文所选TSP 城市数目较多且分布比较紧密，同时半径r的选择相对较大，半径外的城市距离中心点相对较远，因此在计算吸引因子时，即使关联邻域计算了半径外的城市，最终也不会选择其作为下一个经过的城市。故关联邻域能够高效地结合有效信息素，使得减少程序的运行时间。

3.2.3 改进的状态转移规则

在第一类蚂蚁使用原始ACS 状态转移概率公式的基础上，第二类蚂蚁运用了改进的状态转移规则，引入了吸引因子。使得第二类蚂蚁不仅考虑了自身的信息素启发信息和距离启发信息，还结合了与第一类蚂蚁所释放信息素的有关的信息，即吸引因子。综合了种群内的信息和种群间的信息，使得第二类蚂蚁在遍历城市的时候更加容易寻得高质量的解。引入吸引因子的第二类蚂蚁的改进状态转移规则如式（13）、式（14）所示：

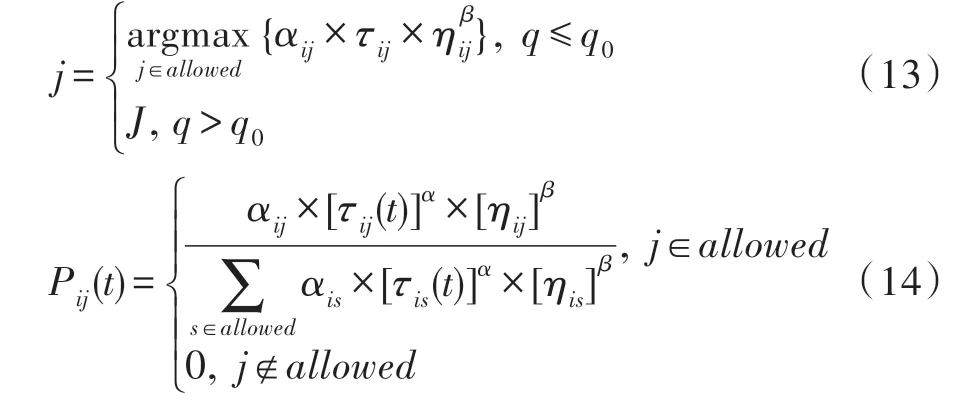
由于在第i个城市选择下一个城市j时，i是固定不变的，因此(i,j)城市之间路径上的信息素浓度决定了吸引因子的大小。式（13）、式（14）中结合了吸引因子，使得第二类蚂蚁在选择下一城市时，更偏向于第一类蚂蚁选择过的较优路径，体现出了吸引因子的正反馈作用。吸引因子加强了两个种群之间的交流，使得第二类蚂蚁遍历城市的时候更具有方向性，加快了算法的收敛速度。

3.2.4 改进的局部信息素更新策略

在ACS 算法中，每条边信息素τij都有一个隐含的限定范围条件，即τ0≤τij≤1/Cbs。当吸引因子加入到局部信息素更新策略中时，由于τ0≤τij，0 ≤αij≤1，因此每条边进行局部更新的时候，其信息素减少的趋势更加缓慢，引入吸引因子的局部信息素更新策略如式（15）所示：

式（15）等价于τij(t+1)=τij(t)+αij ρ(τ0-τij(t))，由于局部信息素更新是减少路径上的信息素，增加算法的多样性，引入吸引因子，再进行局部信息素更新后，路径上减少的信息素浓度的幅度降低，即路径上保留的信息素浓度比没有引入吸引因子的算法的路径上要多。这样在一定程度上抑制了多样性，使得吸引因子的正反馈作用更能体现出来，加快了算法的收敛速度。

3.3 算法流程图

Fig.1 Algorithm overall flow chart图1 算法整体流程图

图1 是本文算法的基本框架。首先引入的吸引因子会使第二类蚂蚁根据第一类蚂蚁释放的信息素更快地寻得最优解，不仅提高了解的质量，也加快了收敛速度。然后在算法的前期结合最大生成树策略，提高了算法的多样性，而在后期结合最小生成树策略，加快了算法收敛速度，从而平衡了算法的多样性和收敛性。

3.4 时间复杂度

从上述算法流程图的分析可以得出，本文算法TREEACS（double-type ant colony algorithm considering dynamic guidance and neighborhood interaction）的时间复杂度为O((n0×k1×m+n0×k2×m)+((N-n0)×k1×m+(N-n0)×k2×m))，式中N为最大迭代次数，n0为，k1为第一类蚂蚁的数量，k2为第二类蚂蚁的数量，m是城市数。因此TREEACS的最大时间复杂度为O(N×k×m)，ACS的最大时间复杂度为O(N×k×m)，MMAS的最大时间复杂度为O(N×k×m)，由此可见，本文算法相比ACS、MMAS 没有改变最大时间复杂度。

3.5 算法收敛能力分析

为了加快算法的收敛速度，提高算法的收敛精度，TREEACS 算法首先结合了动态导向策略中的最小生成树策略，由于最小生成树中的70%～80%的路径与TSP 问题的最优路径是吻合的，因此在算法的后期，每次迭代动态增加属于最小生成树相应路径上的信息素浓度，起到了正导向性，使得算法的收敛能力得到提高。其次TREEACS算法还结合了邻域交互策略，使得第二类蚂蚁在遍历城市的时候，不仅考虑了自身的距离启发式信息和信息素启发式信息，还结合了吸引因子，即第一类蚂蚁所释放的相关信息素信息，让第二类蚂蚁以更高的概率选择那些被第一类蚂蚁走过的较优的路径，不仅对算法起到了正反馈作用，又进一步提高了算法的收敛速度和收敛精度。

下文以实验形式对算法的综合收敛能力进行了分析，结果表明收敛速度和收敛精度都有所提高。综合而言，TREEACS 算法的综合收敛能力优于传统的蚁群算法和一些其他改进蚁群算法。

4 实验仿真

为了检验改进后算法的有效性，本文使用Matlab2017a 对TSPLIB 标准库中的十几个不同规模的城市进行了模拟仿真，并且与ACS、MMAS 进行比较，为了进一步检验本文算法的性能，又与其他两种改进的蚁群算法进行比较。

4.1 实验结果分析

为了有效地验证TREEACS 的性能，本文实验中在TSPLIB 标准库中选取若干城市进行系统性的分析，同时还与经典的ACS、MMAS 算法进行综合比较，分析改进算法性能的优劣。

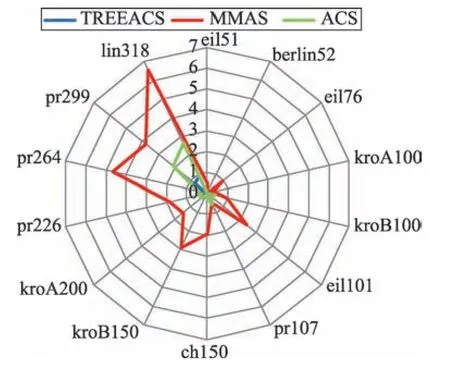
Fig.2 Comparison of error rates of ACS,MMAS and TREEACS图2 ACS、MMAS 和TREEACS 误差率对比图

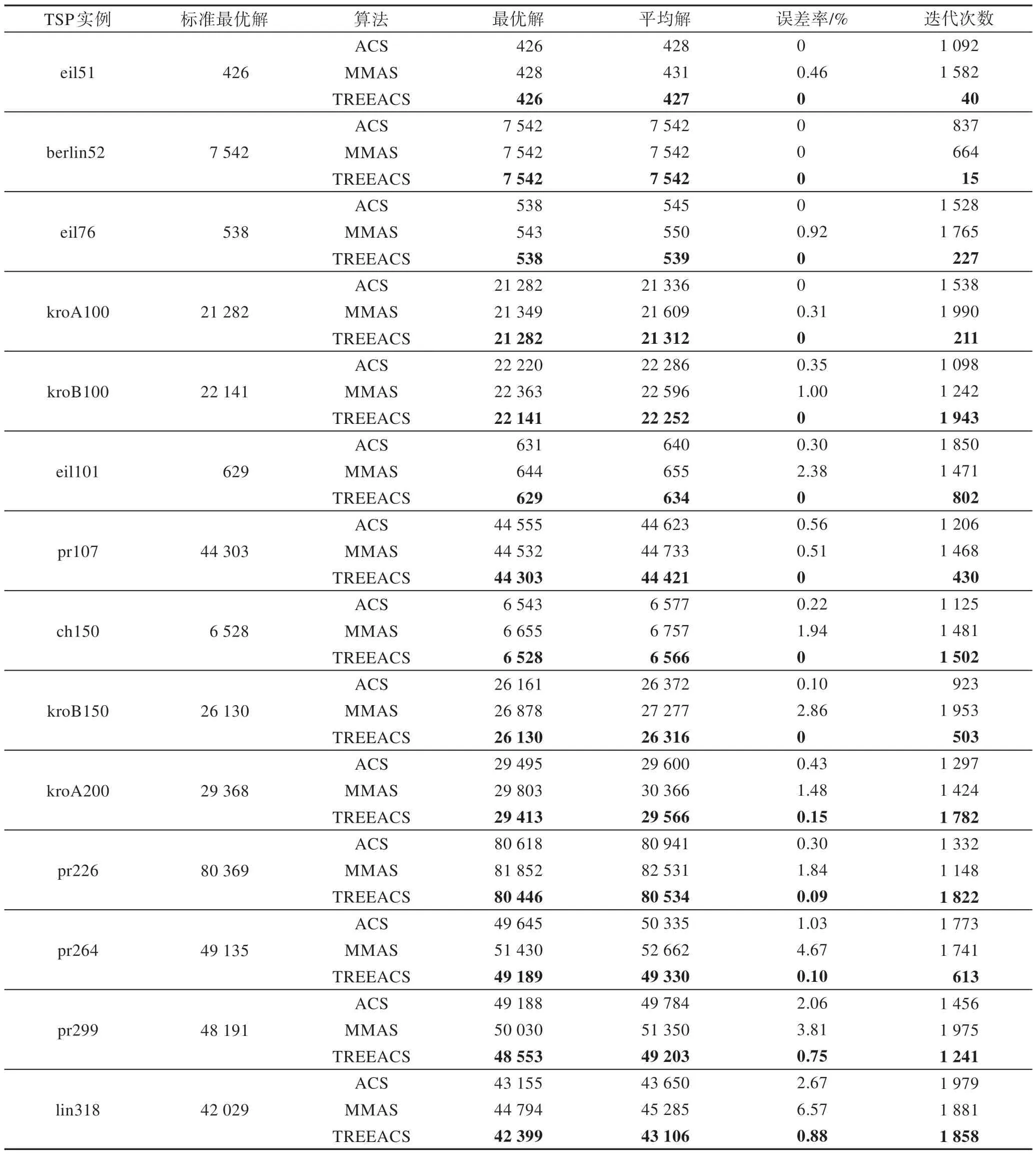
Table 1 Simulation experiment data of ACS,MMAS and TREEACS表1 ACS、MMAS 和TREEACS 仿真实验数据

由图2 和表1 可知，运用本文算法TREEACS，城市数在中小规模以下的9 个测试集中100%的城市是可以得到标准最优解的，城市数在大规模的测试集中，50%以上的城市误差率在0.1%左右，并且无论是中小规模或大规模城市的最优解，平均解和误差率都明显优于ACS 和MMAS 算法。TREEACS 在结合最大生成树的基础上，还加入了MMAS 的信息素限定策略，不但使得算法的多样性加强，还使得算法易于跳出局部最优，从而找到更优解。

4.2 TREEACS 最优解与收敛性对比

图3 表明，运用TREEACS 算法，中小规模的测试集中尤为明显，不仅收敛速度比ACS 和MMAS 更快，而且还能精准地找到标准最优解；在大规模的测试集中，收敛速度依然优于ACS 和MMAS，虽然没有找到标准最优解，但是得到最优解的精度比ACS 和MMAS 都有很大的提高。由于TREEACS 算法结合了最小生成树策略和吸引因子，使得算法在收敛速度方面有了很大的提升。

Fig.3 Experimental comparison of TREEACS with ACS and MMAS图3 TREEACS 与ACS、MMAS 实验对比

4.3 最大最小生成树策略

4.3.1 最大生成树多样性对比

为了验证最大生成树策略对于算法多样性带来的优势，本文分别选取小规模测试集eil51、中规模测试集kroB150、大规模测试集pr264 来进行标准差断点分析。图4 表明，TREEACS 算法在三个测试集中的标准差断点值都要比S-TREEACS（缺少最大生成树策略的TREEACS）算法的标准差断点值要大。这充分说明了加入最大生成树策略明显加强了算法的多样性。

4.3.2 最小生成树收敛性对比

图5表明，TREEACS算法在1 000代之后引入最小生成树策略的时候，收敛速度明显比L-TREEACS（缺少最小生成树策略的TREEACS）算法要快，而且TREEACS 算法会在刚进入1 000 代不久就会跳出局部最优，找到更精确的解，但L-TREEACS 算法则要在迭代末期才能再次跳出局部最优。这也说明了加入最小生成树策略能使算法更快地收敛。

4.4 吸引因子收敛性对比

为了验证吸引因子策略对于算法收敛性带来的优势，本文分别选取小规模测试集eil51、中规模测试集kroB100、大规模测试集kroA200 来进行分析。图6 表明，TREEACS 算法的收敛速度明显比NAFTREEACS（缺少吸引因子策略的TREEACS）算法的要快，且TREEACS 算法的收敛精度也明显比NAFTREEACS 算法的要好。因为邻域交互策略中的吸引因子对算法起到了正反馈作用，使得不仅可以加快算法收敛速度，而且能够提高收敛精度。

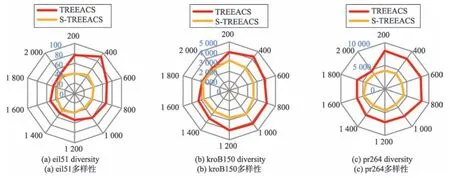
Fig.4 Comparison of standard deviation breakpoints between TREEACS and S-TREEACS图4 TREEACS 与S-TREEACS 标准差断点对比图

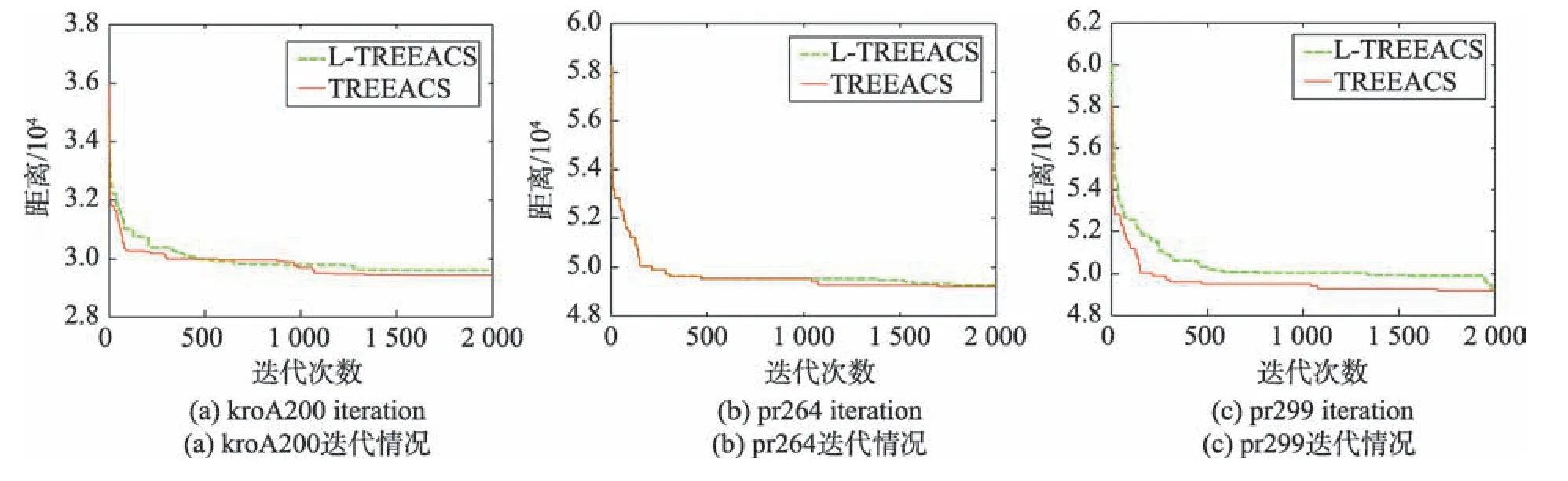
Fig.5 Comparison of convergence of TREEACS and L-TREEACS图5 TREEACS 与L-TREEACS 收敛性对比图

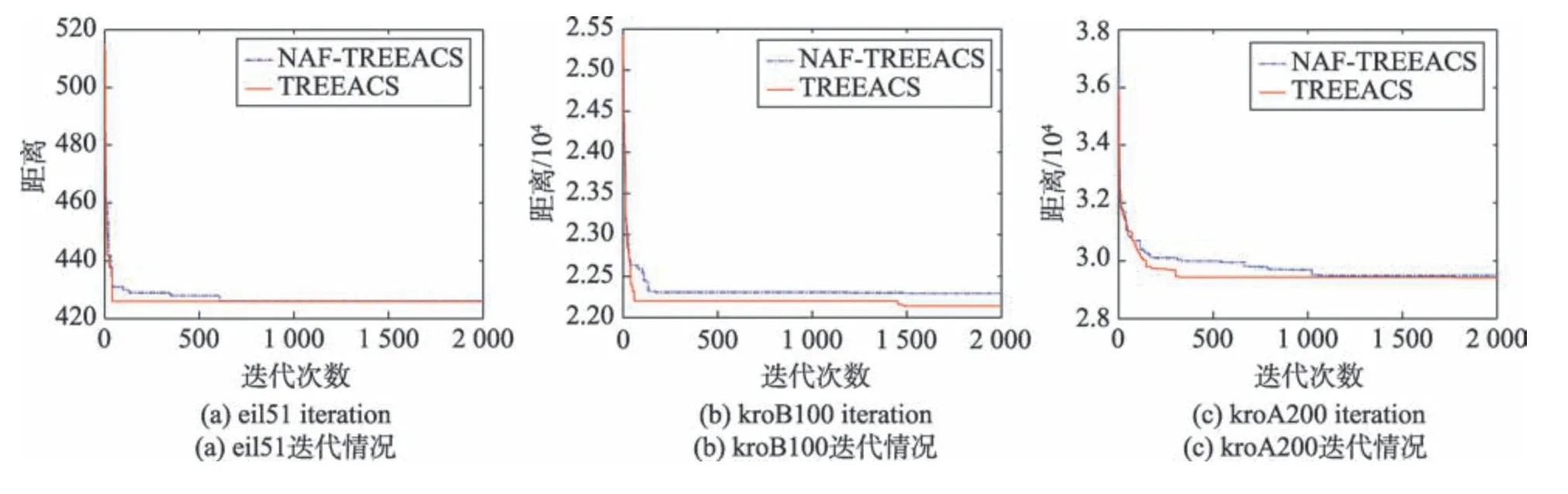
Fig.6 Convergence comparison between TREEACS and NAF-TREEACS图6 TREEACS 与NAF-TREEACS 收敛性对比图

Table 2 Comparison of TREEACS with other improved algorithms表2 TREEACS 与其他改进算法的对比

4.5 与改进蚁群算法及其他算法对比

本文算法与改进蚁群算法及其他算法进行比较，其中D-ACS（ant colony algorithm for heuristic dynamic pheromone update strategy）改进蚁群算法的数据取自文献[24]，改进蚁群算法的数据取自文献[25]，OMACO（object-oriented multi-role ant colony optimization）改进蚁群算法的数据取自文献[26]，IMRGHPSO（improved random greedy PSO based on Hamming distance）改进粒子群算法的数据取自文献[27]，1OGA（1-phase optimal GA）改进遗传算法取自文献[28]。

根据表2 的实验结果可知，本文算法TREEACS无论是在中小规模还是大规模的TSP 问题中，解的精度明显优于改进蚁群算法及其他算法。

5 结束语

由于TSP 问题中存在易陷入局部最优和导向性不足的问题，本文首先引入了动态导向策略，前期在最大生成树策略的影响下，通过增加相应路径上的动态信息素，以使算法达到更好的多样性，并且增加的额外生成树信息素的量是逐代递减的，以防止相应路径信息素累积较快。后期在最小生成树策略的影响下，同样是添加相应路径上的动态信息素，增加的生成树信息素的量是逐代递增的，使得算法的收敛性大大提高。再结合MMAS 的上下限机制，使得每条边上的信息素浓度不会积累得过多而使算法早熟。同时算法结合邻域交互策略，引入吸引因子，发挥了正反馈机制，进一步加强了算法的导向性。

实验结果证明，本文算法在中大规模的TSP 问题求解的精度上有很大的提高，多样性和收敛性也有明显的改善。今后将进一步研究多种群蚁群算法的模型，从而更好地提高算法的性能。