轨迹树层次关系模型多摄像机多目标跟踪研究*

刘冠群，李 婷

1.湖南广播电视大学 网络资源系，长沙410004

2.中南大学 信息科学与工程学院，长沙410083

1 引言

多目标跟踪作为计算机视觉中的一项重要技术，已得到了广泛研究。近年来，学者提出一系列利用目标外观和动态信息的在线和批量方法。但是这些方法在视觉监控中容易受到遮挡，因为它们只使用一个摄像头。特别是在拥挤环境中，比如教室或商店，目标分布密集，容易被各种障碍物遮挡。

为了克服遮挡问题，学者们提出了多摄像机多目标跟踪（multiple cameras multiple targets tracking，MCMTT）问题。例如，文献[1]提出一种针对煤矿井下研究场景的多摄像机多目标轨迹跟踪算法研究，主要针对煤矿井的视频跟踪问题进行有效解决。文献[2]提出基于多伯努利卷积特征多摄像机多目标跟踪算法，该算法利用卷积算法对视频特征进行处理，目的是提高算法的跟踪精度。文献[3]提出一种基于全局分层关联网络的多摄像机多目标跟踪算法，实现目标跟踪精度提升。多摄像机多目标跟踪问题主要分为三类[1-2]：（1）重建/跟踪方法。通过附加视图的测量来克服遮挡或背景杂波导致的目标检测缺失问题。然后应用基于摄像机的跟踪方法来生成目标的轨迹。例如，文献[4]采用协同图在场景中进行目标跟踪，由于跟踪区域的量化存在一定的局限性，协同图存在幻影问题，导致目标位置模糊。然而上述三种方法对背景减法的结果非常敏感。因此，这种算法会受到具有动态或复杂背景的场景的影响[5]。（2）跟踪/重建方法。试图将同一目标的轨迹关联起来，首先用一种基于摄像机的跟踪方法在每个视图独立生成轨迹，然后制定组合问题来关联这些轨迹。例如，文献[6]将轨迹关联问题表述为多维指派问题，这是著名的NP 难题。用一种启发式算法解决了这个问题，即贪婪的随机自适应局部搜索过程，但是其只可解决短遮挡问题。文献[7]采用了高阶动力学模型对轨迹的跨视点关联进行了研究。该算法在没有标定信息的情况下具有很好的鲁棒性。然而，由于高阶动态模型之间的比较需要一个运算来找到大矩阵秩，因此算法计算量很大。（3）统一框架。将重建和跟踪问题表示为统一全局优化问题，通过对整个输入视频序列进行批量处理，取得良好性能。例如，文献[8]尝试使用统一框架的MCMTT 算法。该框架构建了每台摄像机的二维跟踪图，并构建了不同摄像机检测到图像对的三维重建图。然而，所提出的图结构过于复杂。文献[9]提出一种基于超图方法，用单个图来表示重构和跟踪问题，但必须枚举同时检测之间所有可能的重构来构造图。此外，该方法通过二元整数问题公式来求解图形，算法计算量很大。

尽管基准上的性能很好，但是这些算法都是基于批处理的算法，不能在每帧上提供即时跟踪结果，且需要大量计算。对于许多应用程序来说，这是严重限制。此外，算法只使用测量的几何信息。因此，当目标接近度增加时，它们在一致性标记方面存在困难。本文旨在提出一种高效不损失性能的在线MCMTT 算法，该算法与目前最先进批处理算法具有可比性。

2 问题描述

2.1 多目标跟踪问题

给定多目标轨迹检测中，所有摄像机的一组检测结果为D=(di|di=(li,si,ci,ti),i=1,2,…,ND)，其中li、si分别表示图像坐标位置和比例，ci∈(1,2,…,NC)是相机索引，ti表示检测到di的时间戳，di则表示上述界定图像位置的第i个检测。ND是输入检测的总数。定义第j个追踪为，式中是属于Yj的检测索引集。假设每个检测不能由多个目标共享，即对于i≠j，总是满足。航迹是目标在三维世界坐标系下的估计轨迹。当定义为与跟踪Tk关联的跟踪索引集时，Tk、Zk⊂D的检测集可以用中二维跟踪定义。定义作为在时间t从所有摄像机观察到的一组轨道检测。令为目标在时间t的三维估计位置，轨道Tk∈T定义为这些位置估计的序列，式中max({ti|di∈Zk})分别是Tk的起始时间和终止时间。全局假设Hn∈H是一组多目标的估计轨迹，即T的一个子集。将定义为属于Hn的一组索引时，Hn的定义是。

对于可行全局假设，属于同一全局假设的任意两个不同轨道Tk和Tl必须满足以下相容条件：（1）任何两条轨道中都没有共用轨迹，即。（2）避免碰撞，即，式中θs指为避免目标间碰撞所需的最小距离。定义兼容集ℂ，它由兼容轨道的无序索引对组成，即对于所有k,l，满足条件{k,l}∈ℂ。多目标跟踪是寻找最优的全局假设H∗，在满足相容条件的可行全局假设中，H∗具有最大评估值：

式中，{k,l}∈ℂ，∀k,l∈IHn。由于式（1）中问题是NP困难问题，本文提出一种新的在线方案，利用已有解在帧找到式（1）的近似最优解。

2.2 算法框架

图1 给出该方法总体方案，它由四部分组成：轨迹、跟踪、全局假设和修剪。在每个摄像头上，为了在线关联检测，设计跟踪匹配问题的检测方法。然后，生成新的轨迹或用匹配的结果更新已建立的轨迹集。

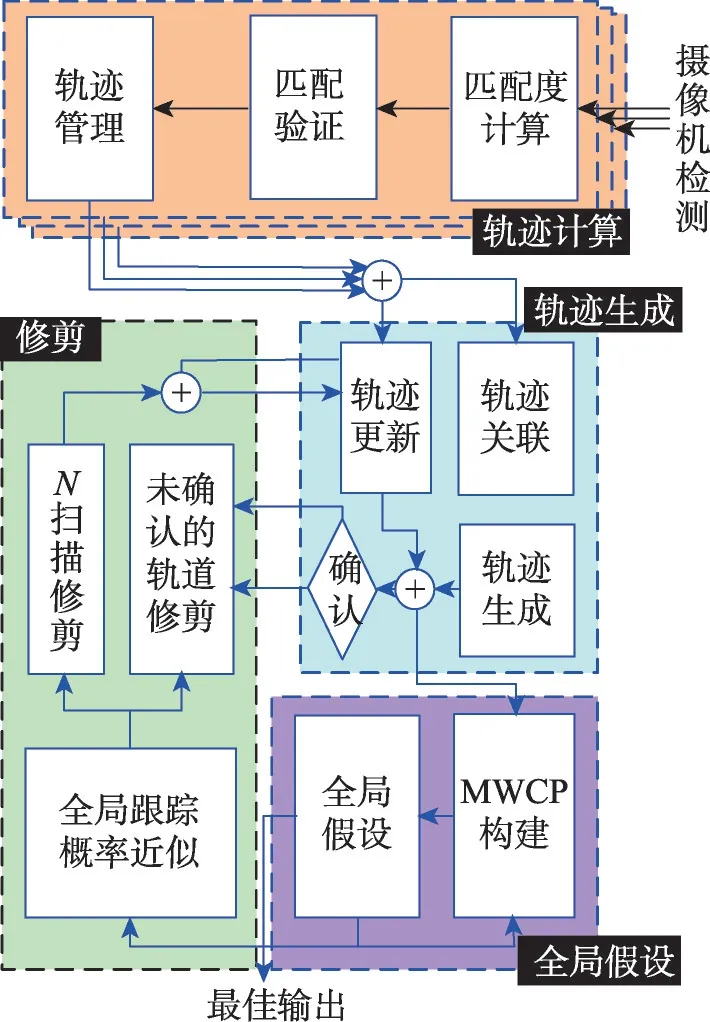
Fig.1 Algorithmic framework图1 算法框架

在全局假设部分，对当前帧中所有轨迹的集合式（1）进行求解。为减少计算量，引用生成模型式（1）的子问题，其包含上一级框架中的KH最佳全局假设集。为了解决NP 难题，采用BLS（Boneh-Lynn-Sshacham）方法，提出了一个良好的初始解和适当的迭代次数，并修改BLS 以生成多个近似最优解。在收集了所有通过解决子问题发现的全局假设之后，将KH最佳全局假设选为Ht。Ht存储在全局假设部分，用于下一帧，并传输到修剪部分。

在修剪部分，根据是否确认一条轨迹，对轨迹应用两种修剪技术。当一条轨迹的持续时间超过某一长度时，该轨迹即被确认。采用Ht计算每条轨迹的近似全局轨迹概率（approximate global trajectory probability，AGTP），并将其用于每种修剪技术中作为标准。然后，修剪信息被传递到轨迹部分，以减少下一帧中的轨迹数量。

2.3 多目标跟踪匹配验证

对匹配检测和跟踪应用进行验证，以增强跟踪健壮性。定义Dt={di|ti=t}是随时间t新检测到的结果，Yt-1作为最近检测时间为t-1 的所有轨迹集，即Yt-1=(Yj|max({ti|i∈Iyj})=t-1)。然后，轨道Yj∈Yt-1与检测di∈Dt之间匹配度为：

式中，wδ(si)指示与si成比例的相邻窗口大小，则差距主要是。通过使用以上前向跟踪，可从中获得，即前一帧中轨迹的最后一次检测。

3 轨迹树层次关系模型

3.1 轨迹模型描述

本节中描述了在线轨迹生成方案，并提出代表每个轨道质量的轨迹分数。此外，还定义轨迹树，表示轨迹间层次关系。

轨迹关联：令{Ω1(Y),Ω2(Y),…} 是整个轨迹集Y=(Y1,Y2,…,Yq)的所有可能分区的集合。然后，所提MCMTT 问题目标是找到分区Ωi(Y)，最能描述目标跟踪。第i个分区定义为是假警报集。表示轨迹集合应来自第i个分区中的第k个目标，称之为关联集。定义所有可能的没有分区索引的关联集：

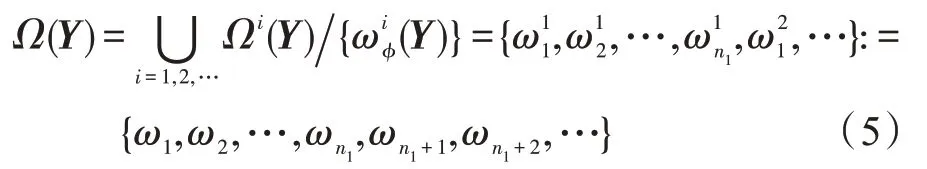
为简化省略参数(Y)，将ωk对应轨迹记为Tk，将ωk的相关检测集记为Zk。定义三种操作：空间关联、时间关联和合并。

操作1（空间关联）如图2 中的T2和T7所示，空间关联是由临时重叠轨迹之间的关联来定义的，这些轨迹应该来自同一目标，使用不同的摄像头。为确定轨迹Yl和Ym是否来自同一目标，提出了空间关联条件，该条件检查轨迹中同时检测之间的距离是否受阈值ε3D的限制，如下所示：

Fig.2 Example of trajectory generation图2 轨迹生成示例

操作2（时间关联）同一摄像头的临时不重叠轨迹间关联，或同一目标不同摄像头间的关联。对于时间关联，前向轨迹Yl和后面轨迹Ym须满足：（1）根据每个目标在每个视图中最多只生成一个检测的事实，Yl和Ym须是暂不重叠的，即{ti|di∈Yl}⋂{tj|∀dj∈Ym}=∅。（2）目标不能突然改变其位置，因此dp（Yl最后一次检测）和dn（Ym第一次检测）在三维空间足够接近。当vmax被定义为目标在一帧内可移动最大距离时，条件是||Φ(dp)-Φ(dn)||2≤vmax×|tp-tn|。

操作3（合并关联）如果两个关联集的联合集满足所有时空关联条件，则联合集也是关联集。这两个关联集称为可合并。其合并操作定义为：（1）如果ωi和ωj可合并，则ωi⊕ωj=ωi⋃ωj；（2）如果ωi和ωj不可合并，则ωi⊕ωj=∅。

3.2 轨迹关系评估模型

考虑四个因素，评估轨迹得分：

（1）重建评估SR(·)，表示轨道位置与检测相同程度。重建评估基于PZ(·)构建，即在特定时间对目标可能性进行检测。将Xtk作为t时Tk跟踪目标位置的随机变量，则重建分数为：

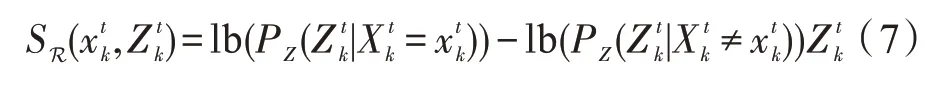
式中，似然度PZ(·)的计算可参见文献[10]有关描述进行计算。

（2）连接分数SL(·)，它考虑了轨道连续位置的几何适宜性。有些运动很难预测，例如行人等，因为它通常是非线性的。因此，只考虑轨道上连续位置邻近性，以确定连接这些位置是否合适。所提连接分数定义为随轨道上连续位置之间的距离发生变化，即：

式中，vmax是一个设计参数，用于模拟行人在一帧内可以移动的最大距离。当远大于vmax时，链接视为无效，此时放弃对其跟踪。参见文献[11]。

（3）初始评估SI(·)和最终评估ST(·)。如前所述，在可见区域中间突然启动或终止的轨迹不太可能。为反映趋势，起始/终止评估定义为：

式中，Ps和Pe分别是目标在可见区域出现和消失的概率。τs和τe是目标与可见区域边界之间距离的惩罚系数。τl是防止长轨迹终止的惩罚系数。是和可见区域边界之间的距离。mB是实验中设定为1 m 的边界。在起始帧附近开始的轨迹不受起始惩罚，因此其起始评估为lb(Ps)。通过这些起始/终止评估，可以避免目标轨迹中出现过多的碎片。参见文献[12]。

（4）视觉评估SV(·)，表示与轨道相关的检测间的视觉相似性。假设目标不会突然改变它的外观，因此每个视图中相同轨迹的相邻检测应该具有相似的外观。对任意轨迹Tk的ωk时间关联处的得分赋值。令是根据其开始时间摄像机c的轨迹有序集合，单位为ωk。检测的有序对集定义为：

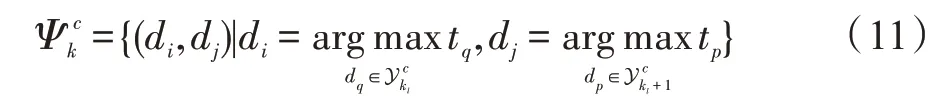
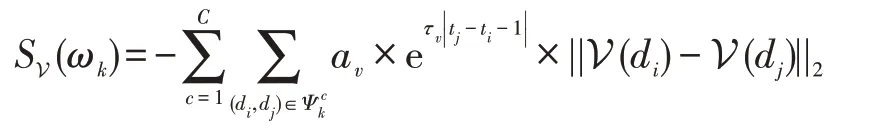
式中，av和τv模型参数随着检测之间的时间间隔增加，视觉相似性置信度下降。参见文献[13]。

最后，利用（1）～（4）所示因素可定义轨迹评估形式：

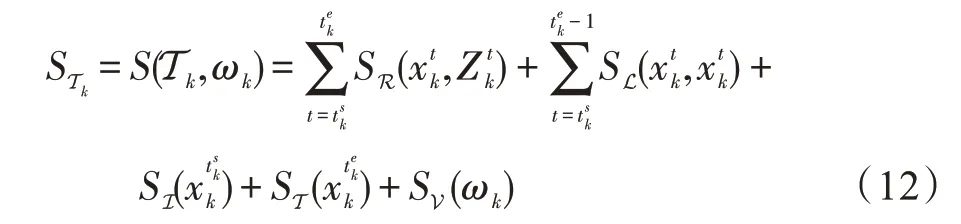
3.3 全局假设

每个MWCP（maximum weight clique problem）由构成，一组轨迹是当前最佳全局假设候选者，假设先前最佳全局假设是。把称为相关轨迹集。它包含三种类型轨道：（1）的轨迹；（2）在当前帧中新生成两个子项轨迹，即；（3）未确认轨迹。

未确认轨迹是比Nconf帧短的轨迹，无法确定它是否为假阳性。因此，不断将未确认轨迹插入轨迹集，即使这些未确认轨迹不在先前解决方案中。则定义为。则 对 于n=1,2,…,KH，每个的MWCP 问题定义为：

式中，与输入视频序列的起始帧Ht-1=∅一样，构造并求解了完整的跟踪集Tt的单重网络控制点。当精确求解多路径控制点时，求解多路径控制点的计算与轨道数成指数比例。

3.4 算法步骤

将Ht定义为Tt中所有可能的全局假设集时，Ti∈Tt轨迹的GTP（global trajectory probability）定义为：

修剪有零轨迹作为轨迹修剪的第一步。由于KH最佳全局假设定义，零轨迹意味着轨迹不属于KH最佳全局假设中的任何一个。

对于已确认的轨迹树，保持每棵树中的所有轨迹是很难的，因为每棵树中的轨迹数呈指数增长。因此，将N扫描后退方法应用于已确认的轨道树。这是基于延迟决策的修剪技术。在找到最佳全局假设后，它会扫描N帧，并根据当前的最佳全局假设确定目标的位置。然后它修剪所有与目标固定位置不兼容的轨迹。从树结构的角度来看，除了当前最佳全局假设中包含轨迹的分支外，它以前在N帧处修剪每个轨迹树的分支。在算法1 中总结了本文的在线方案。

算法1轨迹树层次关系模型

输入：检测视频数据集D。

算法1 中，第1 行是对算法进行参数初始化，第2～第6 行是根据2.3 节内容生成多摄像机多目标跟踪轨迹，第8 行是对轨迹关联性进行计算，然后在第9行中，根据计算的轨迹关联性进行新轨迹生成，第13～第15 行进行最佳轨迹初始化，第20～第22 行是根据3.3 节、3.4 节内容对轨迹结果进行评估，并对其进行轨迹调整和更新。

上述算法中，从计算复杂度角度分析，因为无嵌套迭代过程，因此其计算复杂度是O(N)，具有相对较小的计算复杂度，体现了算法的计算效率。从算法收敛性角度分析，根据第16 行可知，在算法迭代计算过程中，每次选取的是当代进化迭代过程的最佳值，因此该算法可保证多摄像机多目标跟踪过程的收敛。

4 实验分析

4.1 实验设置

（1）实验硬件：处理器CPU 为i5-6400K 3.2 GHz，内存RAM 为ddr4-2 400 GHz 8 GB，系统为Win10 旗舰版，仿真平台选取Matlab2012a。

（2）数据集：选取PETS 2009 数据集作为实验对象，数据集示例见图3 所示。场景中使用3 个集合：S2.L1、S2.L2 和S2.L3。这些装置包括4 到7 个不同的视角，重叠室外摄像机视角。每个视图有数百个帧，以7 frame/s 的速度捕获10～74 个行人。每个场景都有不同行人密度，从低（S2.L1）到高（S2.L3）。基准数据集还通过Tsai 的摄像机模型提供每个摄像机的固有和外在参数。在评估中，给出每帧感兴趣区域内目标位置。

为检验所提成本函数参数和条件对性能精度影响，构造新数据集，即pilsun 数据集，包含来自4 个重叠摄像头的333 frame，每个摄像头捕捉10 个行人，这些摄像头以6 frame/s 的速度密集分布在一个小型室内环境中。数据集还为每个摄像头提供了Tsai的摄像头模型，以及由手工标记的跟踪结果生成的地面实况。

（3）参数设置：比较间隔长度Lc=4 frame，静态特征点阈值δmin=0.05，连续检测之间的最大允许3D距离εΦ=0.5 m，一帧内目标的最大允许三维高度变化εh=0.3 m，相邻窗口大小差异ωδ(si)=0.3×si，避免碰撞的最小3D 距离θs=0.3 m，同时检测最大三维距离ε3D=2.5 m，目标最大三维速度vmax=0.8 m/s，轨迹上允许最大框架间隙δa=9 frame。

（4）作为定量评估的指标，在事件、活动和关系的分类中使用了多对象跟踪MOTA（multiple object tracking accuracy）和MOTP（multiple object tracking precision）指标，这是MCMTT 最流行指标。

4.2 结果分析

（1）参数影响。所提方法的运行参数设置KH=1,5,10,15,20,25,30 和。研究KH和最大值对计算精度和计算时间的影响。图4 显示了处理时间、MOTA 随参数变化的影响实验。

Fig.4 Parametric influence experiment图4 参数影响实验

（2）算法对比实验。为了验证所提求解方案的有效性，将其与变分方案和基线方案进行了比较。图5 显示了每个解决方案的定量结果。对比算法选取：文献[14]仅使用一个MWCP 求解的基线解算方案，没有来自先前全局假设的反馈信息。文献[15]采用一个MWCP 求解的基线解算方案，并采用来自先前全局假设的反馈信息。图6 给出三种对比算法在实验数据集上的1 帧跟踪结果示例对比结果。

根据图5、图6 实验结果可知，当KH=1 时，基线方案优于其他方案。然而这是微不足道的，因为其他方案求解的图形比基线方案小，这意味着它们无法从先前解决方案附近或周围的局部最优解中逃脱。然而，尽管解决的是较小的图而不是基线方案，但当KH值较大时，性能会提高。当KH=5 或更大时，建议方案的性能优于基线方案。当KH=5 或更大时，所提算法（没有初始解决方案）也取得了与基线方案相当的性能。相对于对比算法，本文算法在执行时间和求解精度上均要显著优于文献[14]和文献[15]两种算法，体现了算法性能优势。同时，在图6 实验结果上可直观地看出，本文算法对于目标的跟踪精度更高，可实现对目标的准确识别和追踪。而在对比算法中，文献[14]和文献[15]两种算法的目标追踪精度相对较低，与本文算法具有显著的差异。

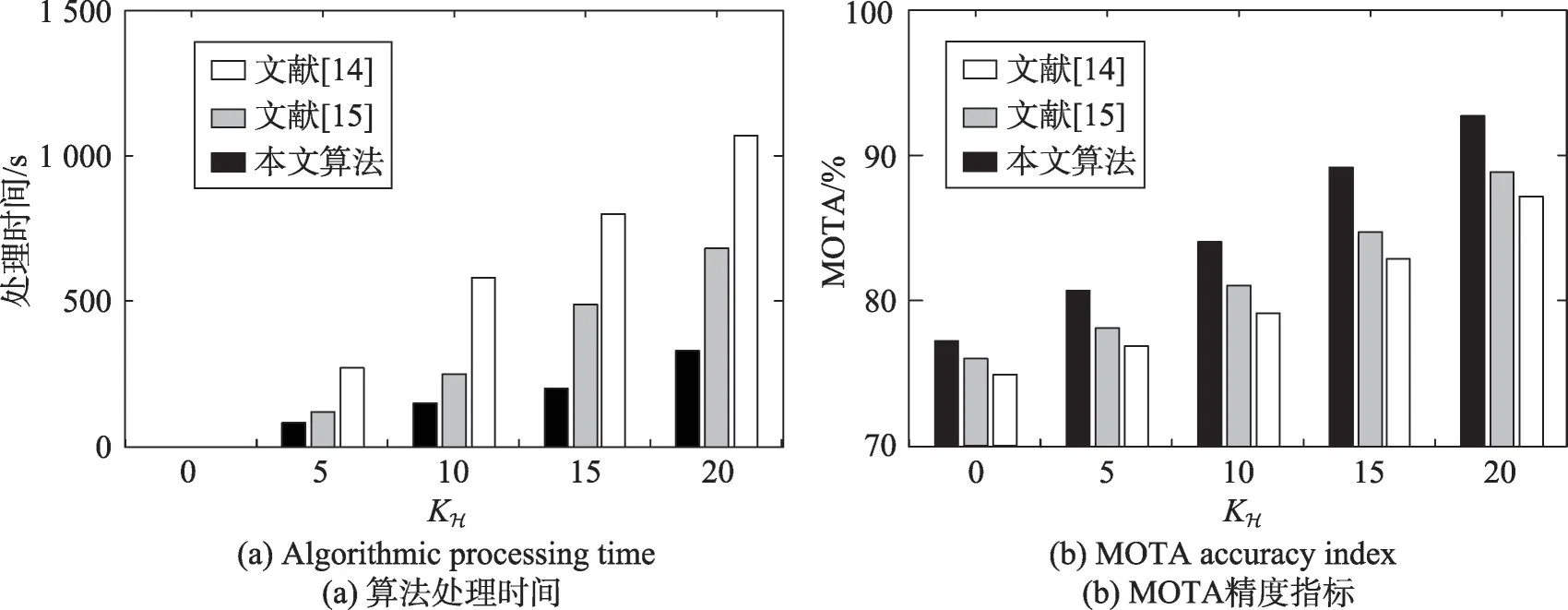
Fig.5 Algorithmic contrast experiments图5 算法对比实验

Fig.6 Comparison of tracking results between two adjacent frames图6 前后两帧跟踪结果对比

5 结束语

本文提出基于MHT（multi-hypothesis tracking）框架的在线MCMTT 算法，该框架是由MWCP 为轨迹关联实现的，可以找到多个对象跟踪，直到当前帧。通过使用轨迹模型和关联条件，所提跟踪算法生成优化的候选跟踪，并拒绝一些不可靠候选跟踪。为解决多目标跟踪问题，提出一种在线方案，该方案根据前一框架中过去的全局假设，生成多个具有小轨道集的多目标跟踪问题。这些子问题的解搜索空间比原来的多目标控制算法小得多，因此该方案大大缩短了求解时间。此外，该方案也比用全轨迹求解多目标控制问题找到更好的解决方案。提出的初始解和迭代次数有助于在迭代次数较少的情况下找到近似最优解。下一步，将重点在算法的收敛性分析方面进行研究，完善算法理论基础。