面向私有二进制协议的报文聚类方法

徐旭东，张志祥，张 献

海军工程大学 电子工程学院，武汉430033

1 引言

协议逆向工程[1]是对未知协议的报文数据或处理这些报文的指令序列进行分析，以获取该协议的格式规范、报文语义或行为规范。协议逆向工程在漏洞挖掘[2]、入侵检测[3]等领域有重要作用。

在网络环境下，通常存在多种协议所生成的报文数据，而不仅仅是单一的报文数据，而协议逆向工程在如此多种的协议报文数据下是不利于开展的，因此在进行协议逆向工作之前需要对报文数据进行聚类，以便对同一类的报文数据进行处理。报文聚类算法针对的协议主要有文本类协议[4]和二进制协议[5]，文本类协议目前有比较成熟的解决方案，如PI[6]和Discover[7]以及之后的改进方案。

对于二进制协议，从数据预处理和聚类方法两方面分析。黄笑言等[8]基于字节熵矢量加权指纹的二进制协议识别，在数据预处理阶段，通过不同字节对协议识别的贡献不同，设定权值并加权构造字节熵矢量；在聚类阶段，使用基于局部加权K-means 算法进行聚类。岳旸等[9]在数据预处理阶段使用AC 算法挖掘出频繁序列特征，使用Apriori 算法搜索频繁序列的关联关系；在聚类阶段，通过改进的K-means算法进行聚类。Tao 等[10]在数据预处理阶段，直接将原始二进制报文作为初始报文向量；在聚类阶段，使用了引入轮廓系数（silhouette coefficient）的K-means算法进行二进制报文聚类。闫小勇[11]在数据预处理阶段，对二进制报文进行截取或补0 的预处理方式，将不等长的二进制报文变为等长的；在聚类阶段，使用距离指数加权的方法自动选取聚类中心，使用密度峰值聚类算法进行聚类。

上述方法大部分针对文本类协议，部分支持二进制协议的聚类方法在数据预处理阶段会存在特征提取不纯，聚类阶段存在簇数不确定等问题。主要原因有两点：（1）二进制协议报文根据使用的场景及目的，会设计出各种不同长度的二进制报文格式，甚至存在同一报文根据不同场景设计不同的变长域，导致同一类型的二进制报文也会存在不同长度的情况；（2）二进制报文是由0 和1 组成的，字段划分以比特为单位，并非传统以字节为划分的文本类协议。这对于二进制报文的聚类是一个很大的挑战。

通过对文献[11]中使用的聚类方法进行分析，发现文中在进行二进制报文的向量化过程中，针对不同长度的二进制报文进行预处理，会采用截断末尾序列，或是对末尾序列补0 的方式，使处理后的二进制报文达到等长的效果，进而进行向量化映射，进行报文聚类。但是其在对二进制报文进行预处理的过程中，会引入一些无关紧要的噪音，这些噪音本文将其定义为序列噪音。这些序列噪音不仅会干扰报文聚类的效果，而且在报文聚类过程中会引起计算量增加，效率降低的结果。

同时，传统的聚类方法在聚类的过程中会存在聚类中心不确定，聚类簇数不确定的问题。本文针对上述问题，（1）提出一种序列项-位置矩阵的频繁项生成方法，根据设置的频繁项支持度阈值挖掘出频繁项；（2）根据生成的频繁项，将二进制报文序列进行向量化的表示；（3）为避免聚类簇数和聚类中心的设定，使用层次聚类[12]中的分拆式层次聚类，对报文的特征向量进行聚类操作，同时使用轮廓系数指导聚类划分，设定轮廓系数阈值，以达到更好的聚类效果。

2 方法概述

二进制报文序列在聚类之前首先要将序列进行特征向量化表示，在进行特征的向量化表示时，首先要进行频繁项的提取，因此本文的工作流程如图1所示。

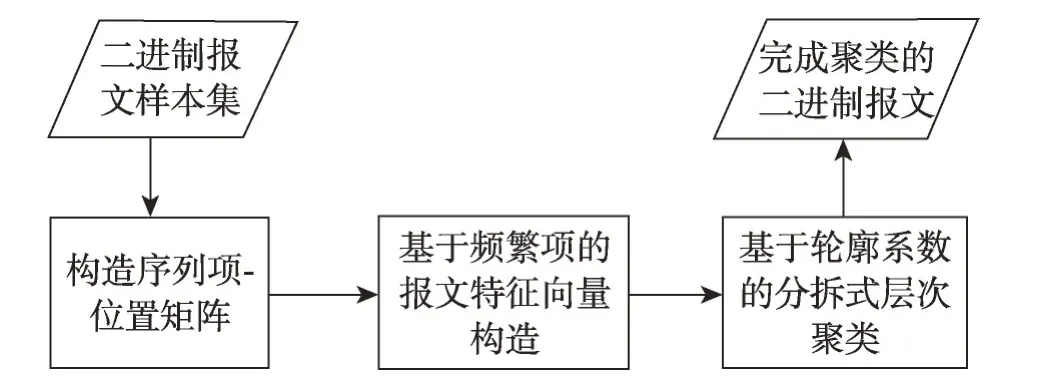
Fig.1 Method step diagram图1 方法步骤图

根据以上思想，主要将工作任务划分为三个阶段：

（1）进行频繁项的构造时，根据n-gram[13]序列化的思想，逐一地对样本集S中所有的二进制报文序列进行遍历，记录每个n-gram 出现的次数C及位置P。为了在频繁项提取时能够尽可能地将存在的频繁项挖掘出，本文引入人工先验知识，参考已有公开的二进制协议的字段长度划分，对n-gram 序列化时的n值进行确定。设置n的取值范围[minN,maxN]，逐一地更改n的大小，重复此步骤，直至记录下所有的n-gram 信息。将记录下的n-gram 信息纳入到序列项-位置矩阵中，完成矩阵构造。

（2）设置支持度阈值threshold1，当某个n-gram的支持度大于阈值threshold1 时，将其纳入到频繁项集中，根据频繁项集中的频繁项，逐一地遍历每条序列，若存在此频繁项，则将此序列对应特征向量的位置置为1，否则置为0。

（3）根据特征化表示后得到的序列特征向量，使用分拆式层次聚类的方法进行聚类，以轮廓系数作为指导，设置轮廓系数阈值threshold2，指导聚类划分，当所有簇的轮廓系数大于threshold2 时，结束划分，完成聚类。

3 基于序列项-位置矩阵的分拆式层次聚类算法

3.1 序列项-位置矩阵的构造方法

本文根据n-gram 序列化的思想，逐一地遍历每条二进制报文序列，摘取片段序列并记录每个片段序列出现的次数C=(c1,c2,…,ci,…,ck)及位置P=(p1,p2,…,pj,…,py)（pj表示对应序列的第一个比特相对于整个序列的偏移位置），由于不同位置的片段可能是相同的，因此对于得到的总的序列片段数目k≤|se|-n+1（|se|表示序列se包含的比特数量），位置数目y=|se|-n+1。

例1 对于序列se=“010001101”，进行n-gram 序列化，当n取6 时，序列化得到的序列为“010001”“100011”“000110”“001101”。并记录次数C及位置P，由于是针对一条序列，因此次数C=(1,1,1,1)，P=(1,2,3,4)，得到的总的序列片段数目y=4。

由于二进制报文字段通常不是等长划分的，如二进制报文序列se={b1,b2,…,bi,bj,…,bn-1,bn}（bi、bj代表字段），|bi|≠|bj|，因此需要尽可能地将完整的频繁项取出，设置n-gram 中n的取值范围[minN,maxN]，本文中minN和maxN的确定需要根据目前已知的、公开的私有二进制协议中的字段长度来设置。设置完毕后，使n由minN逐一递增至maxN。对于每个n，都需要对样本集S中所有的二进制报文序列进行序列化，并记录次数C及位置P。

将序列化后的序列片段纳入到序列项-位置矩阵Mn中，每一个n、C、P对应着一个Mn，根据例1，当n=6 时，矩阵M6如表1 所示。

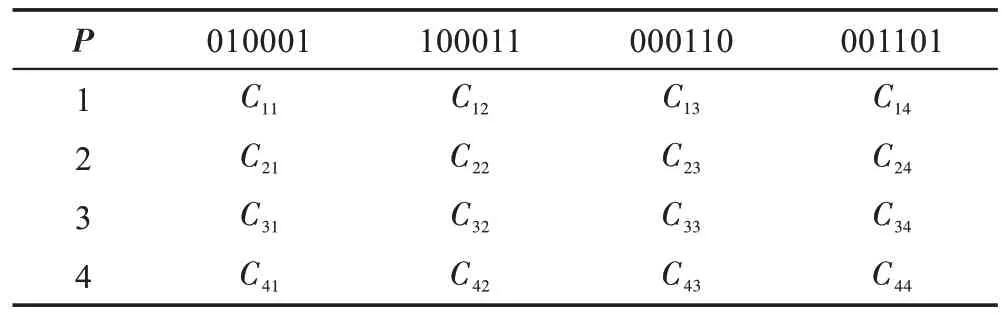
Table 1 Matrix M6表1 矩阵M6

3.2 报文序列特征向量生成方法

为从序列项-位置矩阵中挖掘出频繁项，本文设置阈值threshold1，表示最小支持度，遍历每一个序列项-位置矩阵Mn中的值，即次数cij，当cij/|S|≥threshold1时（|S|为样本中报文的总数），将此次数cij对应的序列片段fi及位置pj作为一个频繁项，加入到频繁项集Fr中，Fr={f1,f2,…,fi,…,fz}，其中fi包含着每个频繁项的比特内容及位置信息，这里将频繁项的位置信息表示为position，以区别于片段序列的位置。

根据频繁项集Fr，生成每一个二进制报文的特征向量FV=(v1,v2,…,vi,…,vz)，其中z=|Fr|，vi=0 or 1。将频繁项集Fr中的每一个频繁项fi与样本集S中的每一个二进制报文序列进行遍历匹配，当二进制报文序列存在所匹配的频繁项fi时，将此二进制报文序列对应的特征向量FV中的vi置为1，反之为0。但二进制报文序列中的字段可能存在些许的位置偏移，导致在进行频繁项fi匹配的过程中，fi.position未必完全匹配，因此本文设置一个容错值allowance。当频繁项fi在fi.position±allowance的范围之内找到了对应的匹配序列，本文同样将fi对应的特征向量FV中的vi置为1；若不在范围内，则依然置为0，最后得到的序列特征向量形如FV=(0,1,1,0…)。

3.3 基于轮廓系数的分拆式层次聚类

3.3.1 t-SNE 的特征向量降维方法

特征向量的维数依赖于所生成的频繁项的多少。

例2 当数据集中的报文序列包含7 类，每一类拥有200 条报文，进行序列化时，取n=5，threshold1=0.143。实验中，产生的频繁项高达498 个，即特征向量为498 维。

如此高的维数，在进行聚类时，运算量巨大，因此在进行特征向量聚类之前，需要对特征向量进行降维操作。

传统的主成分分析法（principal components analysis，PCA）[14]降维是一种线性算法，在将高维数据中不相似的点降低到低维上时，存在相距较远的问题。为了便于在低维空间上用非线性流形表示高维数据，相似数据点必须表示为非常靠近，因此本文选用t-SNE（t-distributed stochastic neighbor embedding）[15]的降维方法。关于t-SNE 的原理不是本文的研究重点，因此不再过多描述。

3.3.2 分拆式层次聚类

分拆式层次聚类是一种自上而下的聚类方式，主要思想是首先将样本集看作是一个整体的簇，再递归地将现有的簇分拆为两个子簇，在分拆的过程中，使用启发式方法进行分拆。

开始的簇包含了所有的样本，S={se1,se2,…,sei,…,sen}，计算样本sei(sei∈S) 对于所有其他样本sei′(sei′∈S)的平均距离，如式（1）所示，距离度量准则可以选择欧式距离或其他度量准则。

选择样本空间S中平均距离最大的样本sei*，如式（2）所示，将它归入新簇N，如式（3）和式（4）所示。

根据此规则，持续地从样本集合S中移除样本，选取的样本sei*满足sei*到S的距离与sei*到N的距离差值最大，如式（5）所示。

在从样本集S中移除样本的过程中，不能无限制地移除，因此要设置终止条件。首先每次在移除样本sei*时，都将重新计算每个样本的平均距离并更新，当所移除的样本sei*不满足式（5），且满足式（6）时，将停止本次移除。接下来，将分别对S和N进行同样的拆分。

分拆式层次聚类没有一个明确的全局目标函数来实现聚类，因此需要设置一个目标，当满足这个目标时，便不再对子簇进行进一步的拆分，本文提出使用轮廓系数来指导划分的方法。

3.3.3 轮廓系数指导聚类划分

轮廓系数表示各簇内部的紧密程度，对于每个报文序列sei，定义其轮廓系数如式（7）所示。

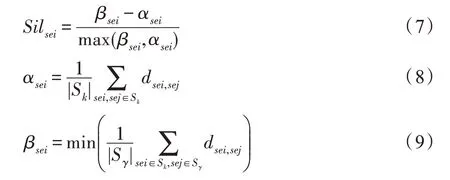
其中，αsei如式（8）所示，表示报文序列sei与其所在簇的其他报文间的平均距离，βsei如式（9）所示，表示报文序列sei与其他簇的报文序列间的平均距离。同样此处的距离度量可以选择欧式距离或其他度量准则。根据公式可以看出，每个报文序列的轮廓系数取值范围为(-1,1)，为了表达簇内部的紧密程度，将轮廓系数进行求和平均，取平均轮廓系数。如式（10）所示，代表该簇的聚类程度好坏，其中Sk表示报文序列sei所在簇。

为能够达到预期的聚类效果，本文引入阈值threshold2，约束聚类是否要继续进行。当平均轮廓系数SilSk＞threshold2 时，表示该簇不再需要进行拆分；当平均轮廓系数SilSk≤threshold2 时，表示该簇仍然需要继续划分，重复3.3.2 小节中的簇拆分步骤，直至所有簇的平均轮廓系数都满足要求，即完成聚类。

4 实验分析

4.1 数据集构造及参数设置

AIS（automatic identification system）协议是船舶自动识别系统的通信协议，是一种二进制协议，DNS（domain name system）、ICMP（Internet control message protocol）及ARP（address resolution protocol）是网络通信中常用的3 种协议。本文通过AIS 采集的真实航行报文数据，以及Wireshark 捕获的DNS、ICMP、ARP报文数据作为原始数据，对原始数据进行逆向处理，获得0、1 组成的二进制报文数据，模拟真实情况下的私有二进制报文数据，作为数据集构造的基础。

为了验证本文方法对于同一协议下，不同报文格式的聚类效果，构造了数据集1，如表2 所示，包含AIS 协议4 类报文格式。其中AIS_1、AIS_4 与AIS_18 的报文数据等长，且与AIS_5 报文数据长度不同；在一定时间内，AIS_1、AIS_5 与AIS_18 报文内容变化较大，而AIS_4 报文内容变化较小。

Table 2 Data set 1表2 数据集1

为了验证本文方法对于不同协议的报文格式的聚类效果，构造数据集2，如表3 所示，包含4 类报文格式。

Table 3 Data set 2表3 数据集2

为了验证本文方法在实际情况下的聚类效果，构造数据集3，如表4 所示，包含同一协议下的不同报文格式，以及不同协议的报文格式，共7 类报文格式。

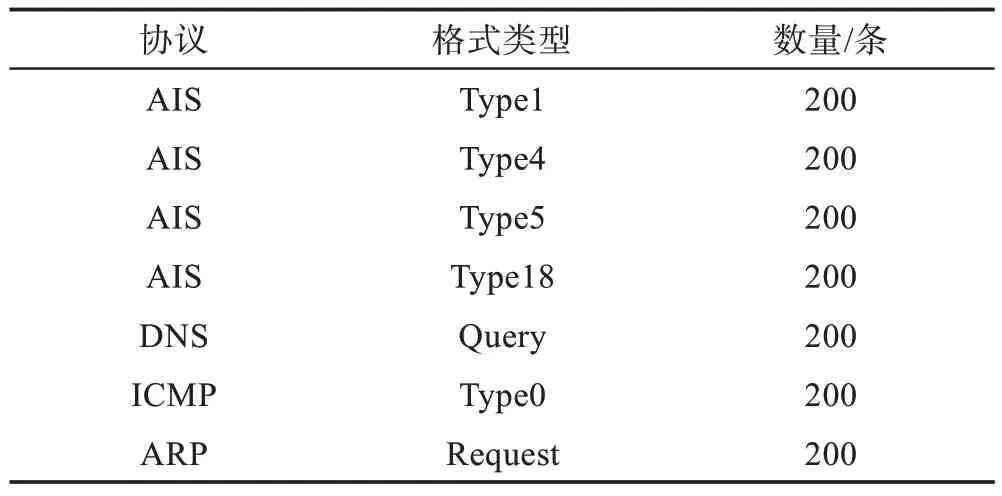
Table 4 Data set 3表4 数据集3

实验过程中，需要对主要的参数进行设置，其中n为n-gram 序列化时的参数，threshold1 为频繁项选取时的支持度阈值，threshold2 为轮廓系数指导划分时的阈值。

本文采用两种经典的评价指标，F1 值和纯净度Pu，如式（14）和式（16）所示。

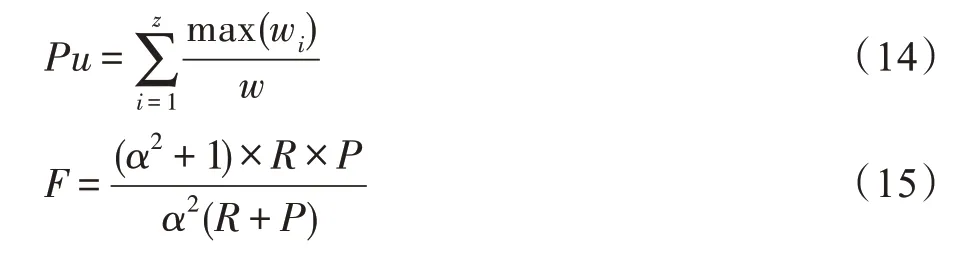
式（14）中max(wi)表示簇i中报文数量最多的种类对应的报文数量；w表示样本数据集中所有的报文数量；z表示聚类簇数。式（16）中F1(t,i)表示在第i个簇，第t类报文的F1 值，F1 值是在F值中的α=1 时所得，F值如式（15）所示，其中R为召回率，如式（17）所示，P为准确率，如式（18）所示。

为了说明总体的聚类效果，样本集总体的F1 值如式（19）所示，其中wt表示样本中t类报文的数量。

4.2 报文特征向量化效果分析与对比

为了直观地观察在报文向量化过程中，所生成的特征向量是否具有代表性的效果，本文使用t-SNE 降维，在二维平面上展示报文向量的分布效果。图2 是在采用频繁项对报文序列进行特征向量化，所得到的特征向量的分布图，其中n=5，threshold1=0.143。

同等条件下，若采用文献[11]中使用的截断报文的方法，截取至报文数据部分的前50 比特，所得到的特征向量分布如图3 所示。

对比图2 与图3 可以发现，文献[11]中的方法无法很好地区分AIS_1 和AIS_5，且与AIS_18 分布较近，这是由于在一定时间段内，AIS_1、AIS_5 和AIS_18 报文数据的内容变化较大，截断的方式无法有很好的特征表达。而经过特征向量化表示的报文序列具有更好的分布效果，特别对于长度较短的报文，特征向量化表示报文具有更加明显的优势。

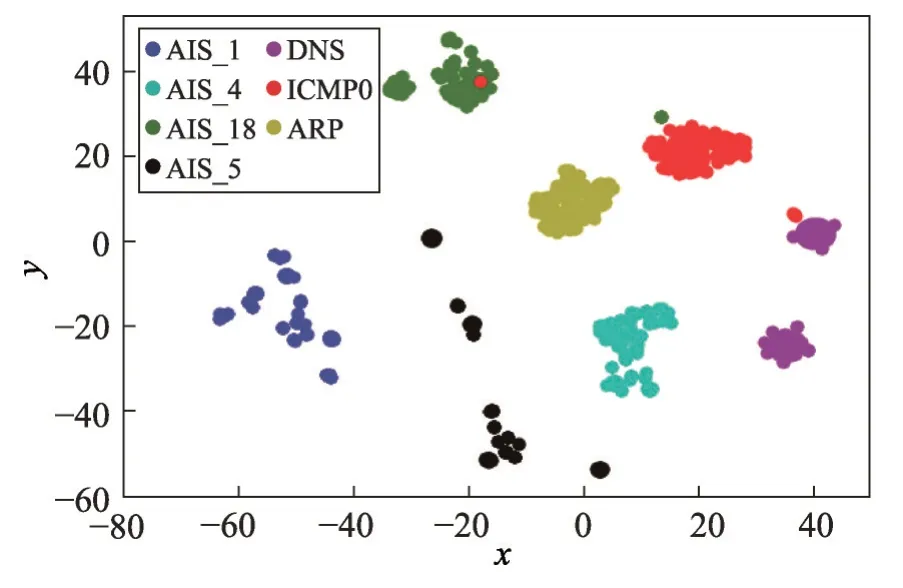
Fig.2 t-SNE vector distribution图2 t-SNE 向量分布图

Fig.3 Message distribution图3 报文分布图

4.3 聚类方法参数及效果分析

4.3.1 序列化中参数n 的分析

在数据集3 的实验上进行分析，将支持度阈值、轮廓系数阈值调整至最佳状态，调整序列化参数n，观察n对于聚类结果度量的纯净度和F1 值的影响，实验结果如图4 所示。

实验发现当5 ≤n≤7 时，纯净度和F1 值处于相对较高的水平，能够达到较好的聚类效果，这反映了以5 比特到7 比特进行频繁项挖掘时，所构造的特征向量最具代表性；当n≤4 时，纯净度和F1 值急剧下降，说明此时的n构造的特征向量不具有代表性；当n≥8 时，纯净度和F1 值缓慢下降，说明聚类效果在缓慢变差，此时n构造的特征向量逐渐不具有代表性。

4.3.2 支持度阈值threshold1 分析

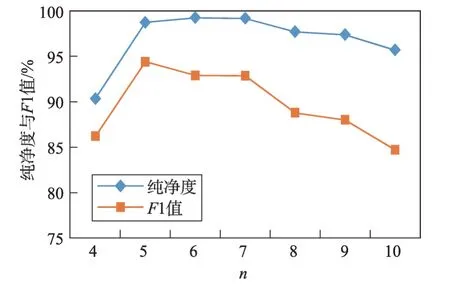
Fig.4 Purity and F1 value corresponding to different n values图4 不同n 值对应的纯净度与F1 值

在数据集3 的实验上进行分析，将序列化参数n、轮廓系数阈值调整至最佳状态，调整支持度阈值threshold1，观察threshold1 对于聚类结果度量的纯净度和F1 值的影响，实验结果如图5 所示。

Fig.5 Purity and F1 value corresponding to different threshold1 values图5 不同threshold1 值对应的纯净度与F1 值

支持度阈值的选择与样本集中存在的报文种类有关，可以观察当threshold1=0.143 时，纯净度与F1值相对较高；当threshold1 ≤0.143 时，纯净度会更高，但F1 值会下降较多，说明许多并非频繁项的序列项被选入作为频繁项，导致同一类型的报文被划分成不同的报文而导致F1 值下降；当threshold1 ≥0.143 时，纯净度和F1 值都会明显下降，说明选取的频繁项构成的特征区分度下降，导致聚类过程中将不同类型的报文聚类成同一簇。

4.3.3 轮廓系数阈值threshold2 分析

在数据集3 的实验上进行分析，将序列化参数n、支持度阈值调整至最佳状态，调整轮廓系数阈值threshold2，观察threshold2 对于聚类结果度量的纯净度和F1 值的影响，实验结果如图6 所示。

Fig.6 Purity and F1 value corresponding to different threshold2 values图6 不同threshold2 值对应的纯净度与F1 值

轮廓系数阈值与最终聚类结果直接相关，轮廓系数越接近于1，说明聚类效果越好。但设置轮廓系数阈值时，若设置过高，会导致过分类的结果，从而导致纯净度很高而F1 值很低。从图6 中观察到，当0.63 ≤threshold2 ≤0.67 时，纯净度和F1 值相对较高，说明此时轮廓系数阈值能够较好地将不同类的报文区分开，同时不会造成过分类的情况。

4.4 聚类方法对比分析

本文选用传统的两种聚类算法进行对比实验，基于划分的K-means[16]算法和基于密度的DBSCAN[17]（density-based spatial clustering of applications with noise）算法，两种对比方法的参数在多次实验过程中选择最优参数设置。在K-means 算法聚类过程中，选择其聚类簇数K=8，在DBSCAN 聚类算法中，参数MinPts=20，Eps 参数通过K-距离曲线确定。在数据集3 的实验上进行分析，3 种聚类方法所得到的纯净度和F1 值如图7 所示。

通过实验结果发现，K-means 聚类算法所得到的纯净度相比DBSCAN 算法稍低，但F1 值却明显高于DBSCAN 算法。而DBSCAN 算法的纯净度比本文方法的98.71%稍高，达到了98.86%，但其F1 值却是3 种方法中最低的。本文方法的纯净度虽然相比DBSCAN 算法低0.15 个百分点，几乎可以认为纯净度水平相当，但本文方法的F1 值相比DBSCAN 提高了6.03 个百分点，相比K-means 方法也提高了2.16 个百分点，因此本文方法能够提高聚类的纯净度与F1值，有效实现了二进制报文数据的自动聚类。

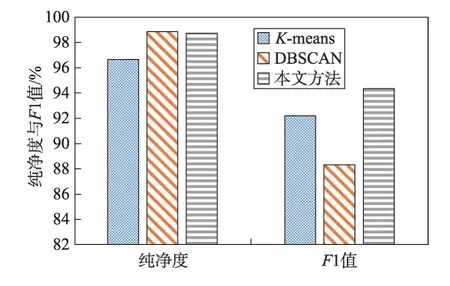
Fig.7 Purity and F1 value corresponding to different methods图7 不同方法对应的纯净度与F1 值

5 结束语

本文所提出的报文特征向量化方法和基于轮廓系数的分拆式层次聚类方法，能够有效地自动实现二进制报文的聚类。通过实验测试发现，报文特征向量化方法相比于传统的截取报文或对报文末端补0 的方法所生成的特征向量更具有报文代表性，更加有助于报文聚类；基于轮廓系数的分拆式层次聚类相比于传统的K-means 算法和DBSCAN 算法，纯净度与F1 值具有更好的综合效果。同时，在下一步工作中，将应用本文聚类方法进行私有二进制协议测试、协议逆向等任务。