设计真实的探究活动 提升学生数学核心素养

栾长伟

(大连市甘井子区教师进修学校)

中共中央、国务院发布的《关于深化教育教学改革全面提高义务教育质量的意见》，其核心内容是落实“五育”并举，实现立德树人。《中国学生发展核心素养》也对探究学生的数学核心素养指明了方向。当前的课堂中，设计能引发学生生疑的问题情境，设计真实可靠的探究过程是落实上述目标的重要环节。然而，仍有很多教师忽略了探究过程所带给学生的探究价值。实际上，要想让学生明白知识的形成过程，教师就要设计科学合理、深度通透的知识探究过程。

一、设计能引发学生生疑的问题情境

数学是促进学生思维发展的核心学科之一。问题情境是现实生活与数学学习之间、具体问题与抽象概念之间的桥梁。它的价值不仅仅是激发学生的兴趣，更应该让学生通过情境建立新旧知识之间的联系并在具体情境中发现问题，进而提出质疑，从而为课堂重点来作铺垫。通常的问题情境创设有如下两种形式。

一是从“数学知识内部”引入。其更多趋近于“复习式引入”，是为了建立新旧知识之间联系的渠道，在学生已有知识的基础上，在学生的“最近发展区”内设置既能引发学生回忆，又能对新知识产生好奇心的问题情境。例如，在教学人教版《义务教育教科书·数学》七年级上册“直线、射线、线段”时，可以在前一节课的“点动成线”的基础上，设计动画效果，从屏幕的外部飞入一个点，再从屏幕中飞走，形成的路线即是直线，直线上的两个点即可以表示为直线AB，射线、线段与其类似。

二是从“生活实际问题”引入。这样一方面容易激发学生对现实生活中数学价值的探求欲，同时也能让学生体会到数学不是孤零零的、没有温度的，而是来源于生活，贴近于生活的。例如，在教学人教版《义务教育教科书·数学》八年级上册“整式乘法”中，教材设计的问题2为：光的速度约是3×105km/s，太阳光照射到地球上的时间是5×102s，你知道地球和太阳之间的距离是多少吗？这一问题既是学生现实生活中的问题，又能让学生产生强烈的好奇心，同时，还有较高的教学探究价值。另一方面，很多实际问题的设计更能凸显数学文化，其实也就是赋予数学教学一种人文情怀。在数学教学过程中，每讲到一个定理，其背后往往都存在一个故事、一个趣闻、一段历史或一些体会，这就会使枯燥的定理和公式有了鲜活的色彩和生动的形象，学生记忆起来会更加深刻。

二、设计“真实可靠”的探究过程

探究过程实际上是为了给学生提供一个亲身经历知识形成过程的机会，并在学生亲自感悟的基础上，进行突出数学品质、提炼数学思想方法的引导，这样才能将知识内化成能力。

例如，在“两点确定一条直线”时，《义务教育数学课程标准（2011年版）》称为“基本事实”，不再称为“公理”。人教版教材上提出的问题是“用几个钉子可以固定一根木条”，从而让学生发现“基本事实”是来自于生活的，这样就具有较好的情境设计意义。事实上，在课堂实践中，教师常用可以粘贴的“纸条”来代替“木条”在黑板上演示。我的想法是“木条要尽量细一些，要尽量趋近于直线”。同时，当将“纸条”撤下后，要用粉笔将撤下的纸条画成“直线”，将固定纸条用的磁铁石画成“点”，而这个过程就是数学中的抽象过程，是数学的核心思想，是学生从实际生活过渡到数学问题的有效途径。

也有的教师设计了这样的探究问题：过一个点可以画几条直线？过两个点呢？如此，相当于直接从数学问题出发，如果能继续追问“过不共线的三个点呢”就会有锦上添花之妙。通过“不同个数的点画直线”都会得到同样一个结论，学生才会从内心“承认”，“过两点可以画一条而且只可以画一条直线”。

再如，在教学人教版《义务教育教科书·数学》八年级上册“平方差公式”一课时，教材设计了如下问题：计算下列多项式的积，你能发现什么规律？（1）（x+1）（x-1）=______；（2）（m+2）（m-2）=______；（3）（2x+1）（2x-1）=______。

此情境的创设有两个缺点，一是每个多项式的第二项均是数字，所以才会有学生总结说“一个单项式与一个数字的和乘以这个多项式与这个数字的差”；另一个缺点是所有的两个多项式都满足“两数和与两数差的积”的形式，这对于学生归纳能力的培养是存在不足的。归纳结构的前提是对已有结构的分类，所以要在问题中加入不满足平方差条件的形式。如，（3x+2）（3x-4）=_______；（2x-y）（3x+3y）_______。然后，可以追问：“等号左边的哪几个多项式具有共同特点？他们积有什么特点？”

从实际课堂的总结中可以发现，关于平方差的描述，学生会总结出两种规律，一是“两个数的和乘以这两个数的差等于这两个数的平方差”，即平方差公式；另一种是“同号两项的积与异号两项的积的和”，这是课堂上学生真实的总结，是建立“真实可靠”的探究过程所得到的学生自然生成。在此基础上，让学生再举出满足结构的多项式乘积，验证自己的猜想是否正确，这才是从特殊归纳出一般，再回到特殊的思维过程。

最后是关于用几何图形验证平方差公式的过程，很多教师不理解为什么要用图形验证。实际上，图形的验证过程是一种“数形结合”的方法体现，也是在后期学习中，例如“勾股定理”探究的一种方法铺垫。教材中图形设计的意图很明显（如图1）。

图1

此图可以看成是边长为a的正方形减去边长为b的正方形，再将剩下的①部分拼接到②位置，得到变成为（a+b）的正方形；或者理解为长为（a+b），宽为（a-b）的长方形的长边上截取宽为b，长为（a-b）的长方形（即②），并将其拼接到①位置。相比之下，从学生的课堂的认知反应来看，北师版教材中关于平方差公式的验证更符合学生的认知规律（如图2和图3及例题）。

图2

图3

例题：如图2，边长为a的大正方形中有一个边长为b的小正方形。

（1）请表示图2中阴影部分的面积。

（2）小颖将阴影部分拼成了一个长方形（如图3），这个长方形的长和宽分别是多少？你能表示出它的面积吗？

（3）比较（1）和（2）的结果，你能验证平方差公式吗？

就是说，将两个图形分开，看起来会相对更清晰一些。在图2的提示下，我们可以尝试设计更加开放的问题探究：

师：有的同学将边长为a的正方形剪掉一个边长为b的正方形，将剩下部分按虚线裁剪成①和②两部分（如图4），并将这两部分分别拼成梯形（如图5）和平行四边形（如图6），请你借助图5和图6完成平方差公式的证明。

师：有的同学在边长为a的正方形的内部剪掉一个边长为b的正方形（如图7），你能用两种方法表示①②③④部分面积和吗？

图4

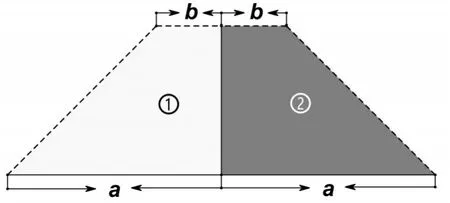
图5

图6

图7

经过以上完整的验证过程，学生经历了从整式乘法的计算寻找共同规律，从而猜想出平方差公式，再用文字和符号两种语言进行描述，最后通过图形设计开放性的面积验证策略，这是探究的实际价值。学生得到的不仅仅是一个广为应用的平方差公式，更是以后进行命题探究的基本方式。

基于核心素养的初中数学课堂，教师应该坚守以人为本的教育理念，围绕数学核心知识，通过创设恰当的问题情境，提出有效的数学问题，开展适度的深度探究。应引导学生自主地学、联系地学、批判地学、通透地学，进而在知识与技能形成的中，在情感与态度升华中，在思想与经验的积累过程中培养学生的数学核心素养。