开发校本教材 提升学生的数学思维能力

付 颖

（福建省福州市乌山小学）

数学思想是指人们对数学知识内容和所使用方法的本质认识，它是从某些数学认识过程中提炼和概括出来后被反复证实的数学规律。数学方法是数学思想的表现形式和得以实现的手段。掌握了数学思想方法，在一定意义上来说就是掌握了数学的精髓。数学思想方法也是增强学生数学观念，形成良好思维能力的关键要素之一。因此，在数学课堂教学中应该注重数学思想的渗透，要通过各种方式展示数学思想方法，提高学生的数学思维能力。

一、从实际问题出发，明确挖掘校本思维教材的必要性

数学思想在我国数学课程目标的发展中经历了从无到有的变化。《义务教育数学课程标准(2011年版)》中提出：“数学课程不仅包括学习数学的结果，也包括数学结果的形成过程和其中所蕴涵的数学思想方法。”同时，《义务教育教学课程标准（2011年版）》也不断强调要重视在教学中渗透数学思想方法。而在实际课堂中，对数学思想培养的落实情况如何呢？

在人教版《义务教育教科书·数学》一年级下册第二单元“20以内的退位减法”的教学结束后，我们对学生计算方法多样化的掌握情况进行了调查，题目是“请用多种方法计算14-6”。绝大多数学生都能正确地写出计算结果，但有三分之一以上的学生写不出思考过程。而此题除教材中出现的2种方法（想加做减、破十法）之外，还有5种不同的方法：连减法、多减再加、多加再减、同加法、同减法，就因为教材中没出现、教师不关注，因此没有几个学生能够写出教材所示之外的第三种方法。

这项测试反映了教师和学生缺乏对数学思想的关注，教材中已有的锻炼数学思维的机会都不够重视，教材中没出现的就更可想而知了。这样不仅限制了学生数学思维的发展，也抑制了学生创造性的发挥。面对如此的教学现状，我校负责第一学段教学的教师率先尝试，群策群力，通过深入挖掘教材，一起开发了校本思维教材。

二、以学生发展为本，找准思维教材的定位

在开发教材的初期，我校很多教师都想要借助市场上的奥数思维培训教材，选取适用的部分作为校本思维教材的蓝本。可是，通过仔细阅读，我们发现，奥数思维培训教材起点较高，并不适用于学习程度中等及以下的学生。结合我校“乐思、善思”的办学理念，若强行引入教学，不但不能培养学生学习数学的兴趣，反而会适得其反。为此，我们再次翻开了数学教材，通过对数学教材的再度研究，我们得出了新的思路，那就是校本思维教材不应是高深莫测的，而应像数学教材那样既能够让学生看得懂，又有浓厚的钻研兴趣。最关键的是，要能渗透数学思想方法，提升思维能力，即校本思维教材应立足于教材，在思维开发程度上又略高于教材。

关于校本思维教材的编排形式我们也进行了定位，校本思维教材需要为学生创设轻松活泼的学习氛围。首先，我们确定了校本思维教材的主人公：两个漫画卡通形象阿U和阿美；其次，在编写上采用两个动漫形象对话的形式轻松展开教学；最后，基于第一学段的年龄特征，校本思维教材的内容呈现采用数形结合的方式。

三、以课内教材为本，设计多种类型的校本思维教材

在对教材进行较为深入地钻研和发掘的基础上，我们归纳了适合做校本思维教材内容的三种类型。

（一）新知的拓展延伸

数学校本思维教材可以是对课内知识的拓展。

一类是对新授课例题的拓展。我们深入挖掘新授课中能有效拓展学生数学思维能力的课例，将之赋予丰富的数学思维方法，编写入我们的校本思维教材。

如我们将“9的乘法口诀”这节新授课设计为校本思维教材“找9的乘法口诀规律”。以往的课堂中，教学目标是通过发现规律熟悉9的口诀，而我们借助9的乘法口诀来培养学生的观察能力，做了极大的创新。学生在前面已学过1到8的乘法口诀，他们极为熟悉口诀的形成和含义，因此完全具备独立学习9的口诀的能力。9的口诀中有许多规律，这些规律有些是显性的，有些是隐性的，而其中隐性的规律对学生的观察能力提出了极大的挑战，这些规律的发现不仅对记忆9的口诀这个知识性目标有很大的作用，而且其中着蕴含数形结合思想、优化思想等多种思想方法。在观察活动中，学生可以积累经验，提升数学思维能力。

另一类是新授课后的拓展延伸。新授课学习之后，根据教学內容设计有针对性的思维拓展题，不仅能促进学生对课内知识的掌握，还能提升学生综合运用的能力，使学生获得最大程度的发展。

如在学习了人教版《义务教育教科书·数学》一年级下册“找规律”之后，我们设计了“创造规律”这一校本思维教材。（如图1）此校本思维教材的设计，不仅帮助学生复习了课堂中的各种不同规律，还有效沟通了图形之间的规律和数之间的的规律，渗透了数形结合的思想，并且激发了学生挑战自我的热情，培养了创新意识。

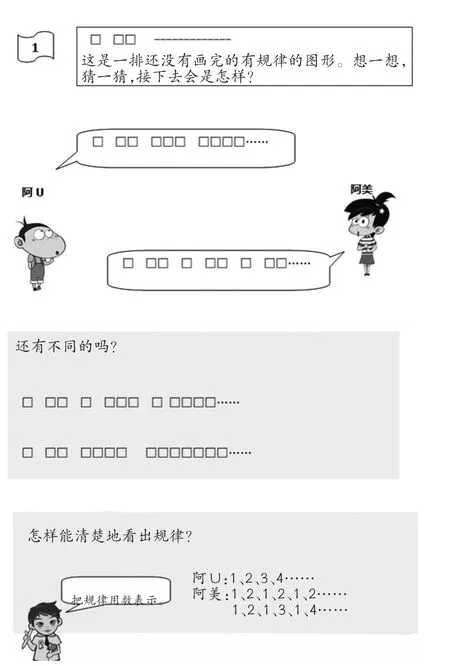
图1

（二）练习的拓展延伸

数学校本思维教材也可以是对课内某一道或某一类练习的拓展。数学教材中有些拓展性的练习设计得很好，而且这些题目中都蕴涵有丰富的数学思想方法。如果只作为一道练习题让学生花少量的时间去训练，不仅学生难以掌握，而且只是就题论题，实则可惜。为此，我们将其拓展，变成了数学校本思维教材。这一类的教材编写，从新课到练习编写都是一次极具创新性的原创设计。

这节课我们的教学目的绝不是解决这类排队问题，而是不断让学生自己尝试通过画图解决问题，渗透了数形结合和符号化思想。

（三）“数学广角”或综合实践的拓展延伸

数学校本思维教材可以选材于部分综合实践活动课程。这是人教版教材中新增设的一个内容。以往的课堂上，很多教师要么略过不教，要么仅仅是简单的介绍。但若是仔细研读教材，我们就会发现：这些综合实践课程，往往都是对一个单元所学知识的提炼，具有很强的探究性，对于学生增强应用数学的意识，提高数学思维能力、实践能力和解决问题的能力是很有帮助的。这些课程足以让学生深切体会数学的应用价值及趣味性，提升学生的数学思维能力。如果把这样的内容专门进行一定的改编，就会使是非常好的数学校本思维教材。

图2

图3

图4

教材中的“数学广角”也可以开发为数学校本思维教材，但必须是对教材中的内容有更为深刻的思考，对教材进行不同角度的改编。如人教版《义务教育教科书·数学》三年级下册的“搭配”一课，很多教师在教学时所想到的都是要渗透教参中提到的“有序思考、符号化思想”。但我们发现，用这种方式教学，当在看似难度并不大的变式题出现时，大多数学生都会认为这道变式题并不属于搭配问题，并且学生会呈现茫然、不会解答的状态。经过不断实践探究，我们终于取得了一定的突破，有了新的发现：原来我们忽视了“建模思想”在其中的重要作用，于是我们就把这一课改编成了我们的数学校本思维教材（如图2至图7所示）。

图5

图6

图7