论深度学习导向下小学生数学画图解题能力的培养

陈若霖

摘 要：为了探讨深度学习引导对小学生画图解题能力培养的实际效果，文章结合日常教学经验，通过模拟直观的数学情境，分别从创新思维、动手实践、多样化教学等方面举例进行了论述。研究表明，通过深度学习引导，让小学生利用数形结合思想画图解题，不仅可以加深其对数学基本知识点的理解，还有利于其数学能力、数学思维和数学兴趣的培养。

关键词：深度学习;画图解题;数形结合

中图分类号：G623.5 文献标识码：A 收稿日期：2019-10-19 文章編号：1674-120X（2020）11-0038-02

所谓“深度学习”，是指学生在教师的引导下，积极参与具有挑战性的学习，并在这个过程中感受成功和学习的乐趣。通过深度学习体验，学生不仅可以掌握教材中的核心知识点，还可以在整个学习过程中乐此不疲。将深度学习理念引入小学数学教学中，可以让看似空洞的数字问题和复杂的文字描述变得更加浅显易懂，提高学生的解题准确率、数学解题能力、空间想象力和表达能力，使其在独立完成数学练习时能够举一反三。

一、层层深入，挖掘学生的创新思维

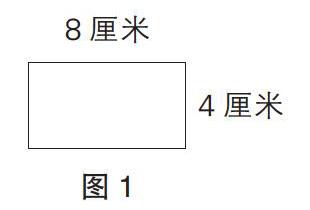
在深度学习理念引导下培养学生的画图解题能力，是培养学生创新思维的重要途径。“面积求解”是小学三年级数学的重要知识点，是学生从认识几何图形到解答几何问题最基本的转化。如何通过画几何图形解决几何问题，这是引导学生深度学习的关键。对简单的几何面积求解，大多数的学生都可以通过课堂上教师讲解的方法独立进行。例如，“已知长方形的长和宽分别为8厘米和4厘米，求长方形的面积”这类问题，学生可以通过简单的面积求解公式进行解答，即长方形的面积=长×宽，那么求解可得：8厘米×4厘米=32平方厘米。不理解的学生可直接画图求解，一目了然，如图1。

在上述基础上，教师可以对学生进行深度学习引导：“已知正方形的边长为10，用剪刀剪去一个三角形缺口，剩余边长为8，求图形面积”，如图2（a）。对学生而言，直接求解五边形的面积难度较大，那么教师就可以引导学生观察图形：此图形实则为一个正方形减去一个等腰三角形，只要掌握了正方形和三角形的面积求解方法，就很容易计算出题目答案，如图2（b）。因此，可求解图形面积为：10×10-（10-8）×（10-8）÷2=98。

上述思路求解此类题目比较简单，教师可进一步引导学生思考其他解题方法，如将图形进行分割后计算。

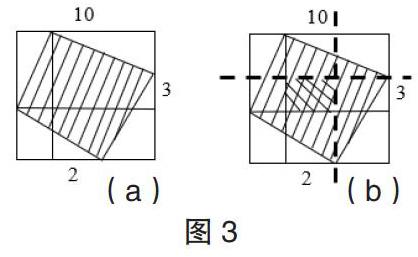
例如，图3（a）中正方形的边长为10，阴影部分四边形在正方形边上所截长度分别为2和3，求解阴影部分四边形的面积。这类面积求解需要学生充分结合有效条件，通过画图做相应的分割线，利用面积相等转化进行求解，所以求解可得：阴影部分的面积=（10×10-2×3）÷2=47。

这样，让学生通过“填补”的方法解决面积求解问题，由填补法到分割法，不但提高了学生画图解题的能力，而且促进了学生创新思维的培养。

二、动手实践，深入理解几何概念

小学数学画图解题强调让学生动手实践。动手实践，不仅可以激发学生的学习兴趣，提高其实践能力，还可以促进学生深度学习。

例如，为了让学生能够具体、深入地理解几何图形面积的概念，能对比出不同形状的图形面积大小，如图4（a）所示，教师可以让学生在课前准备一些大小一样的小方片，并在课上自己动手用小方片分别铺满两个图形，如图4（b）。然后，教师进行适当引导，让学生观察铺满图形所用小方片的数量并进行比较，从而得出“用的小方片数量越多，图形面积越大”的结论，进而促进学生对几何面积概念有更深入的理解。由此可见，在课堂上增加数学实践操作，不仅可以加深学生对理论概念的记忆，还能拓展他们的论证思维，引导他们进行深度学习，进而让其得出自己的正确判断，为后续引出几何图形的面积求解公式做铺垫。

在小学数学画图解题的教学过程中，教师通过让学生动手实践实现深度学习，不仅可以促进学生对基础知识的掌握，同时也可加深学生对新知识点的印象。

例如，在教学小学五年级“立体几何图形的体积求解”时，教师可以引导学生通过作图细化题设条件，然后通过动手实践，让几何问题变得更加直观。例如，有一张长为20厘米，宽为10厘米的长方形铁皮，在四个角上分别裁下一个边长为2厘米的正方形后做成一个长方体容器，求容器的体积。初看题设，可将长方形铁皮被裁剪后的基本形状画出来，如图5（a）所示，这样对题设中的条件就有了一个更清晰的认识;再通过动手实践，选择一张纸片，在四个角上分别裁剪相同大小的正方形，然后折叠成一个长方体，这样对长方体的长、宽、高就有了比较直观的认识，分别为（20-2-2）厘米、（10-2-2）厘米、2厘米，如图5（b）所示。那么由长方体的体积计算公式可得：该长方体体积=（20-2-2）×（10-2-2）×2=192立方厘米。

从画图解题，再到实践操作的深度学习，让学生在动手的过程中解决数学问题，这是当前素质教育阶段的重点。

三、一题多解，多思路解决难题

小学阶段的数学问题，往往可以通过一种甚至多种方法进行求解，尤其是一些应用性的题目。教师可以让学生在画图解题的过程中掌握基本的解题方法，再延伸出其他的解题思路，从而加强深度学习。例如，在小学四年级“工程问题”学习中，原计划完成一条100米的管道铺设任务，前4天铺设了整条管道的25%。问：同样进度下铺设完剩余的管道还需要多少天？

在常规教学方式下，教师通过画图解题的思路进行讲解，如图6，从“工作效率”启发学生进行解题，即运用“工作量÷工作时间”“工作量÷工作效率”公式解答此类题目。

解法一：100÷（100×25%÷4）-4=12（天）;

解法二：（100-100×25%）÷（100×25%÷4）=12（天）。

此外，由于小学三年级学生已经学习了分数的相关概念，所以在深度学习理念引导下，教师还可以通过讲解分数的意义及“工程问题”的相关概念，启发学生利用分数进行解题。那么，解题方法还有：

解法三：1÷（25%÷4）-4=12（天）;

解法四：（1-25%）÷（25%÷4）=12（天）;

解法五：4÷25%-4=12（天）。

由此可以看出，通过画图解题实现“一题多解”，可以让学生的解题思维更加发散;通过深度学习引导学生运用已学知识进行拓展，可以培养学生解决数学问题时敢于尝试和思考的学习能力。正如上述图2中的面积求解，在掌握常规解题方法的同时，教师可以引导学生思考其他的解题思路，即我们所讲的“分割法”，将不规则的图形分割成简单图形进行求解，解題思路如图7所示。

解法一：将图形分割成一个梯形加一个长方形，可得图形面积=梯形面积+长方形面积，即S=（8+10）×2÷2+

8×10=98;

解法二：将图形分割成一个三角形加一个梯形，可得图形面积=三角形面积+梯形面积，即S=8×（10-8）÷2+（8+10）×10÷2=98;

解法三：将图形分割成三个三角形，可得图形面积等于三个三角形面积之和，即S=8×（10-8）÷2+10×10÷2+8×10÷2=98。

四、结语

通过深度学习引导，利用画图解决数学问题，使隐形条件显性化、直观化，可以有效提升小学生在数学课程中分析问题的能力。在深度学习理念引导下，运用画图分析问题的过程除了可以运用上述所说的思想方法外，还可以用假设条件的方法、分类比较的方法等。

在小学数学教学过程中通过深度学习引导，不仅可以增加数学的趣味性，还能调动学生学习的自主性，从而培养学生的实践能力。

参考文献：

[1]程明喜.小学数学“深度学习”教学策略研究[J].数学教育学报，2019，28（4）：66-70.

[2]喻 平.小学数学深度学习的路向[J].教育视界，2019（4）：4-7.

[3]赵耕楠.小学生数学画图解题能力的培养[J].基础教育研究，2019（3）：39-40，43.

[4]刘志荣.小学数学教学中学生画图思考能力培养的调查研究[J].经贸实践，2018（19）：265.

[5]蒋安娜，唐恒钧.数学深度学习：内涵、实践模式与展望——基于文献的分析[J].中学数学杂志，2018（1）：3-6.