具有磁芯的无线电能传输系统非线性分析与控制
2020-06-09程远锋邓其军
吴 雨,周 洪,程远锋,朱 傲,褚 平,邓其军
(武汉大学 电气与自动化学院,湖北 武汉 430072)
0 引言
随着大功率电动汽车的普及,磁谐振式无线电能传输(wireless power transmission,WPT)的发展也突飞猛进[1-2]。但应用在电动汽车上的WPT系统存在着许多亟待解决的技术难点,例如电能传输过程中传输效率和传输功率低的问题。为了降低系统损耗[3-4],提高系统传输效率[5-6],增大系统传输距离[7],文献[8-9]在磁耦合结构中加入磁芯。然而,由于磁芯材料的磁导率会跟随线圈电流变化,使线圈的电感随线圈电流动态变化[10-11],从而导致系统的传输特性发生改变,甚至出现非线性现象。
非线性现象的存在会对系统的稳定性和安全性造成影响。为了让系统稳定地运行,需要对系统进行控制。当前,对于混沌控制的研究已经比较成熟,针对不同类型的非线性系统有不同的控制方法。经典的控制方法主要有参数扰动方法[12]、滑模变结构控制方法[13]和反馈线性化控制方法[14]等。参数扰动方法在应用时,系统进入到受控状态所需要的时间长,控制效率低。滑模变结构控制方法多用于离散系统,由于含磁芯的WPT系统离散过程极其复杂,因此该方法不适用。反馈线性化控制方法对系统参数不确定性极其敏感,在实际的系统中应用具有局限性。因此,本文提出了一种自适应控制方法,基于拉塞尔(LaSalle)不变原理设计控制器,使系统达到稳定状态。
本文首先对加入平板磁芯的线圈进行分析,利用有限元分析法对具有平板磁芯的线圈建立仿真模型,得到线圈的非线性电感的数学模型。然后,在空线圈WPT系统的基础上,建立具有非线性电感的系统状态空间方程。使用数值分析法对建立的模型进行非线性分析,利用MATLAB软件对系统的状态方程建立Simulink框图,进行系统的非线性特性分析。最后,考虑到非线性系统状态方程是非自治的系统方程,提出了一种自适应控制方法。根据函数中的平衡点,用一个负反馈增益的环节使系统稳定在平衡点周围,系统的输出量由不规则振荡变为周期振荡。
1 具有平板磁芯的WPT系统电路模型
1.1 WPT系统电路建模
WPT系统及其简化模型如图1所示。该系统主要由电源、高频逆变、发射、接收、高频整流和负载6个部分组成,发射线圈和接收线圈组成的磁耦合机构是整个系统的核心部分,通过磁场实现能量的转移,当发射线圈与接收线圈处于谐振状态时传输效率最高。电源是整个系统的能量来源,电流经过高频逆变电路部分,转换为系统需要的高频交流电,从发射线圈以电磁场能量的形式转移到接收线圈,再经过高频整流电路给负载供电。WPT系统模型如图1a所示。
在系统的发射线圈和接收线圈是空心线圈时,将WPT系统模型中的逆变部分、整流部分与负载简化,得到如图1b所示的WPT系统的简化模型。
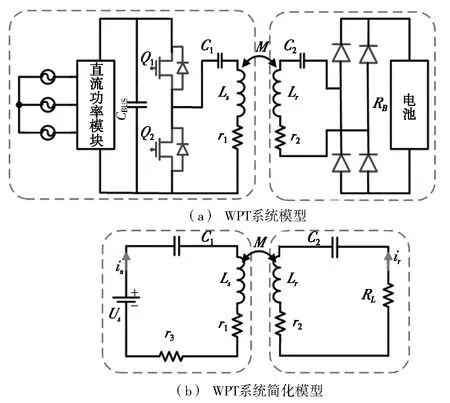
图1 WPT系统及其简化模型
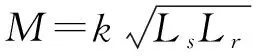
根据基尔霍夫(Kirchhoff)电压电流定理,得到WPT系统简化模型的状态空间方程[15]:
(1)
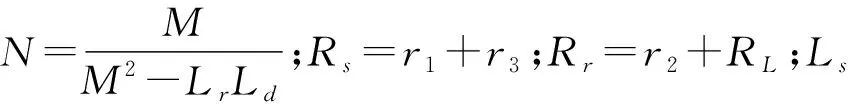
1.2 含平板磁芯的线圈建模
对于磁耦合结构来说,线圈缠绕方式和线圈材料等因素对其传输性能有很大影响。综合考虑,采用平板磁芯作为磁屏,不仅能更明显地增大系统的传输效率,而且还能在传输区域产生更均匀的磁场。磁芯材料采用具有高磁导率的Mn-Zn铁氧体SM-50[16],初始磁导率为5 000 H·m-1。铁氧体材料作为磁芯时,电导率远小于磁导率,本文只考虑铁氧体的磁导率和厚度对电感的影响。线圈采用利兹(Litz)线,由单股直径为0.1 mm的超细漆包线绞制得到,线圈采用单侧式缠绕方式,绕制成平面方形结构。线圈绕制参数如表1所示。

表1 线圈绕制参数
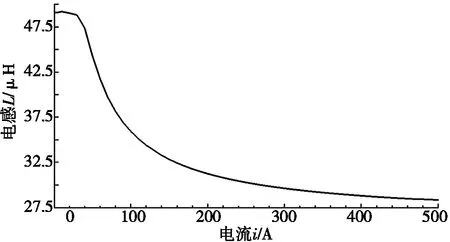
图2 电感-电流关系曲线
虽然在磁耦合结构中加入磁芯,会增强线圈所处环境的磁场强度,但是磁芯材料磁化曲线并不是线性,导致磁导率不是定值,在计算电感时存在很多问题。即使平板磁芯的结构非常简单,其计算公式也很复杂。为了得到具体的电感公式,采用Ansoft有限元电磁仿真软件对平板磁芯线圈进行仿真,使用麦克斯韦(Maxwell)三维线圈参数构建模型,仿真得到模型在表1参数下的电感-电流关系曲线,如图2所示。
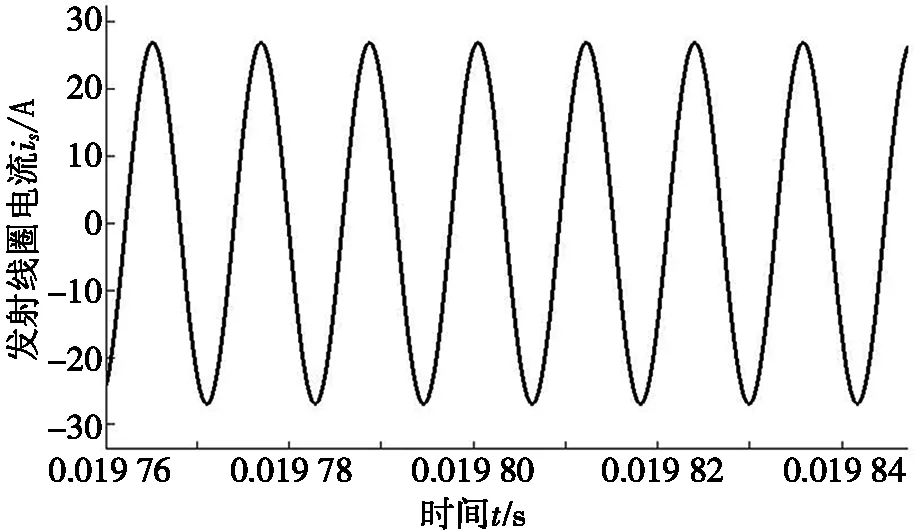
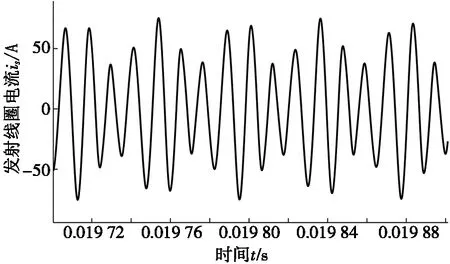
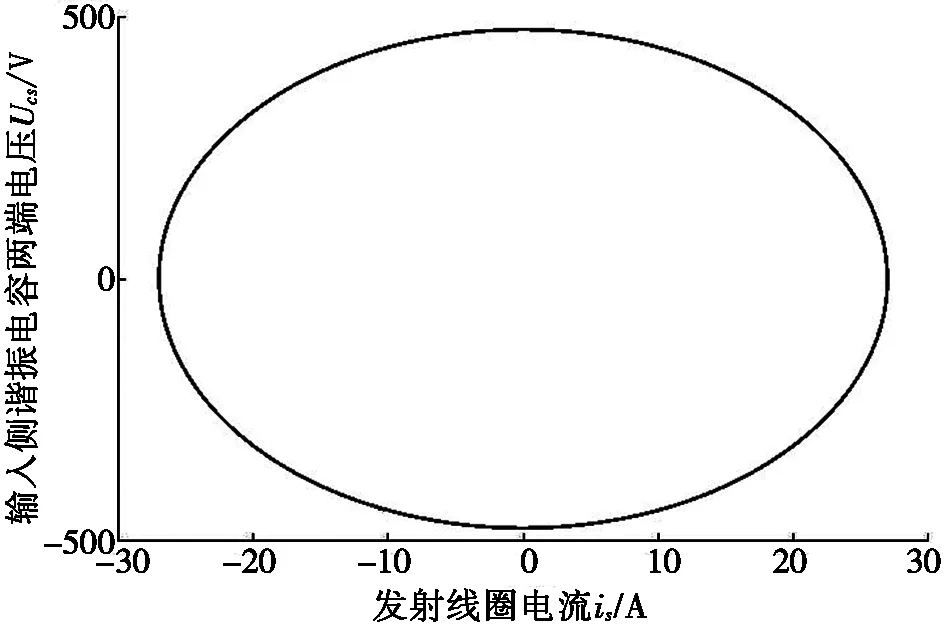
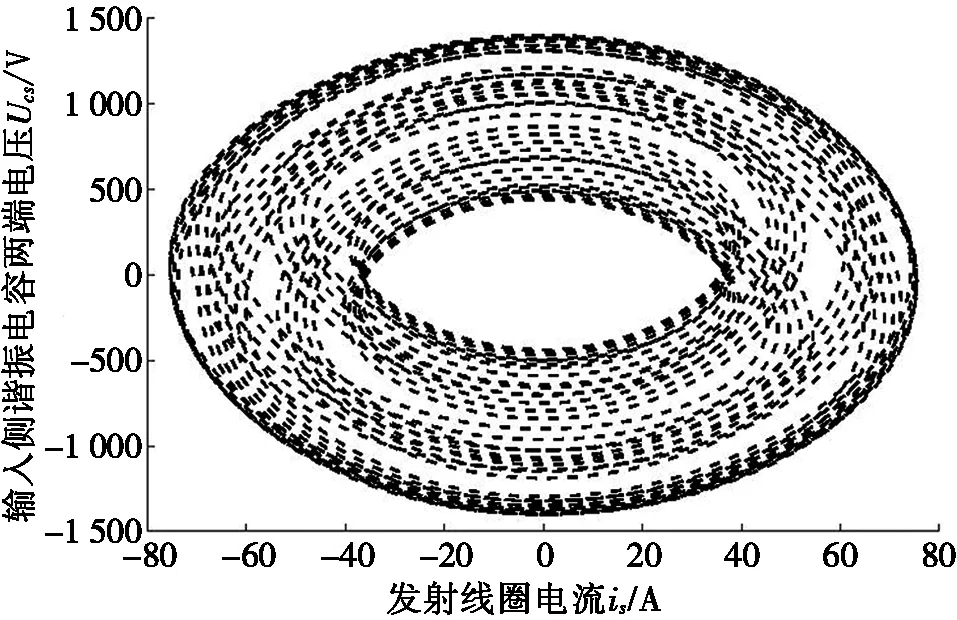
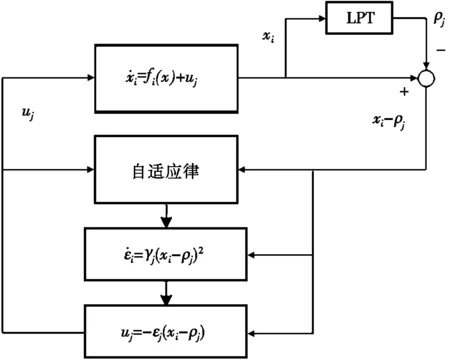
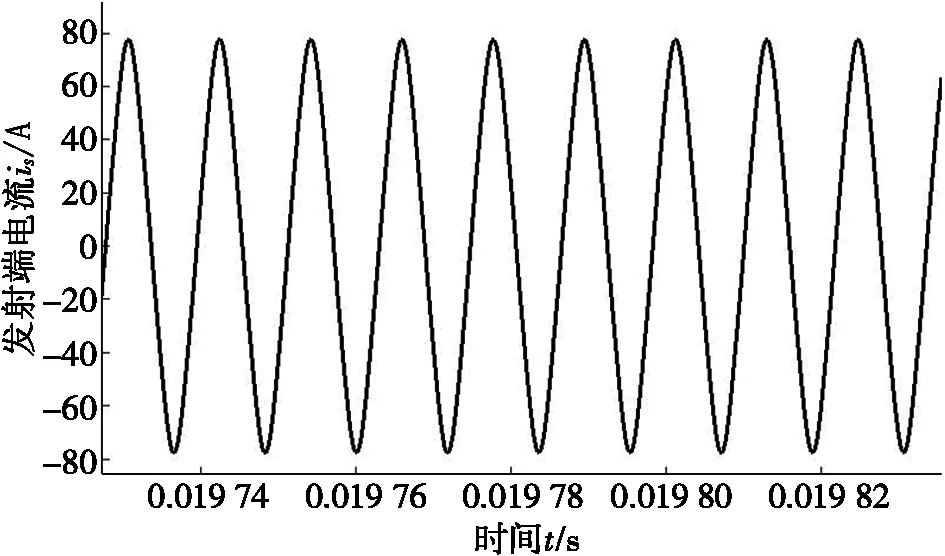
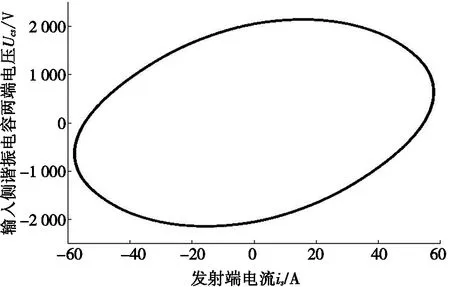
由图2可以看出:线圈中加入平板磁芯之后,电感随着电流的增大而逐渐变小。电感-电流的关系可以分为3个阶段:i≤30 A时,电感可视为定值;30 A 利用分段函数法[17]建立非线性电感的数学模型,可得到线圈电感与通过线圈电流的关系,如式(2)所示。 (2) 其中:i为线圈瞬时电流,A;L(i)表示线圈电流为i时的瞬时电感,μH;L0为线圈初始电感,μH;Ls0为电流足够大时线圈饱和电感,μH;I0为电感刚发生变化时的电流,A;Is为电感刚好达到饱和时的电流,A。 根据仿真模型,可得数学模型中的I0=30 A,Is=120 A,L0=49.5 μH,Ls0=28.5 μH。 图3 数学模型与仿真模型结果对比 为了分析数学模型与仿真模型的差距,利用MATLAB软件对两个模型进行比较,结果如图3所示。目前电动汽车WPT系统中,线圈电流最大不超过80 A[18],根据图3可知:当i≤80 A时,数学模型与仿真模型基本一致。因此,可以用数学模型代替仿真的电感电流变化关系。 将式(2)代入到简化WPT系统的状态方程(1)中,得到含有平板磁芯的WPT系统的状态方程。 含有平板磁芯的WPT系统是复杂的非自治系统,其解析解难以直接求得,故系统的稳定性等性能分析相当复杂。可利用MATLAB软件数值法对系统进行分析[19],得到发射端和接收端在不同输入电压下的动态响应图,进一步研究加入磁芯之后整个系统的非线性特性。 根据实验室现有的WPT系统设备,可以得到WPT系统的仿真参数,如表2所示。 表2 仿真参数 输入不同电压时,发射线圈电流is的时间响应曲线如图4所示。不断改变输入电压US,发射线圈的电流波形随着输入电压幅值的增大逐渐变化。当输入电压幅值较小(300 V)时,整个电路正常振荡,如图4a所示;当输入电压幅值增加至850 V时,电路处于不正常振荡,出现谐波, 如图4b所示。 (a) US=300 V (b) US= 850 V图4 输入不同电压时,发射线圈电流的时间响应曲线 经过上述仿真可以发现:在系统中加入磁芯之后,由于非线性电感的存在,基波电流发生畸变,产生谐波[20]。线圈的电感是影响谐振频率的关键因素,电感的变化会引起系统的自谐振频率偏离系统的工作频率,从而使线圈出现谐波,造成传输效率下降。 谐波的存在对整个系统会造成极大的干扰,表明能量发生了泄露,影响系统的工作效率。其次,谐波会使电路中的元件产生谐波损耗,降低系统的效率,引起电器元件过热,由于线圈的趋肤效应,会增大线圈的有效电阻,增加系统的功率损耗。谐波的存在,影响电器元件的正常工作,使电器元件发生过热,会加速电路元件的老化。 为了更方便地看出系统是否出现混沌现象,采用上述同样的参数,仿真得到发射线圈在不同输入电压幅值下的混沌吸引子相图,如图5所示。 当输入电压幅值为300 V时,输入线圈侧电压电流关系如图5a所示,系统轨道为圆周期1轨道;当输入电压幅值逐渐增加到850 V时,输入线圈侧电压电流关系如图5b所示,系统的轨道变大,周期轨道超过20个,出现混沌现象。 (a) Us=300 V (b) Us=850 V 图5 不同输入电压幅值下输入线圈侧电压电流关系 根据上述分析,在输入电压幅值达到850 V时,无线电能传输系统出现了混沌现象。传统的控制方法与系统的动力学模型紧密相关,控制目的是稳定混沌吸引子的不稳定轨道。但是,许多情况下系统的稳态位置是未可知的,在这种情况下,需要自适应定位系统的稳态位置。本文基于具有可变反馈增益的闭环控制器,利用LaSalle不变性原理,设计了一种自适应反馈控制器[21-22],达到了控制系统稳定的效果。 从稳定性分析的角度来介绍自适应控制的基本方法。考虑非线性系统: (3) |fi(x)-fi(y)|≤kmax|xj-yj|; ∀x,y∈Rn,i=1,2,…,n,j=1,2,…,n。 (4) 在系统(3)的状态方程的等式右边添加控制律uj,则系统方程为: (5) 自适应控制律uj的设计需要保证输出无稳态误差。在无法知道系统稳定点位置时,可以构建一个无反馈扰动,实现自动预测与稳定固定点,这个功能设计方式如下: (6) 对非线性系统设计的自适应反馈控制器如下: (7) 利用自适应反馈控制方法对具有平板磁芯线圈的系统状态方程进行控制。为了方便测量控制状态变量,本文选取x=(UC1UC2isir)T为状态变量,发射端线圈电流is为输出量y,占空比d为控制变量,加入控制项uj之后,受控表达式为: (8) 图6 自适应控制系统框图 根据状态方程,得到施加控制后系统的框图,如图6所示。图6中,LPT表示低通滤波器,由控制器uj通过实际信号的输出量与LPT滤波的差值得到,同时与可变控制强度εj有关。 根据上述加入控制项的系统模型,利用MATLAB软件进行数值仿真分析,此时同样采用表2的仿真参数。 当输入电压幅值设置为850 V时,设置控制器的初始值为λ1=0,λ2=0,γ1=0,γ2=0。由原始系统状态方程可知此时系统处于混沌状态。采用同样的仿真参数,改变控制器的参数为λ1=1,γ1=2,λ2=0.05,γ2=0.05,设置仿真步长为0.000 01 s,发射端电流稳定后的状态如图7所示。 根据图7可以看出:当US=850 V时,施加控制,发射端电流达到稳定状态时,电流波形为正弦波形,无分岔现象,峰值与图4b中最大值相同,控制效果显著。 为了更方便地看出系统是否出现混沌现象,采用同样的系统参数与控制参数,仿真可得到US=850 V时输入线圈侧电压电流关系,见图8。 对比图5b与图8控制前后输入线圈侧电压电流相图可知:输入电压US=850 V时,在添加控制器之前,系统的输出量表现为无规则振荡,出现混沌现象。而在添加自适应反馈控制器后,系统的输出量快速收敛至周期振荡状态,系统的混沌与波动最终稳定,系统的周期轨道从超过20个控制到1个,系统恢复到正常运行状态,说明设计的控制器具有良好的混沌振荡抑制效果。控制前后系统的状态对比,如表3所示。 图7 US=850 V时施加控制,发射端电流稳定状态 图8 当US=850 V时施加控制,输入线圈侧电压电流关系 表3 施加控制器前后系统对比 本文提出了一种针对平板磁芯线圈的电动汽车无线充电系统的控制策略,解决非线性电感导致的WPT系统非线性问题。利用有限元分析方法,建立了含有平板磁芯线圈的非线性电感模型,进一步利用数值分析方法分析了系统的非线性特性,给出了系统出现混沌现象的条件。针对系统出现的混沌现象,设计了自适应反馈控制器。仿真验证了设计的自适应控制器对加入平板磁芯的WPT系统具有良好的控制效果。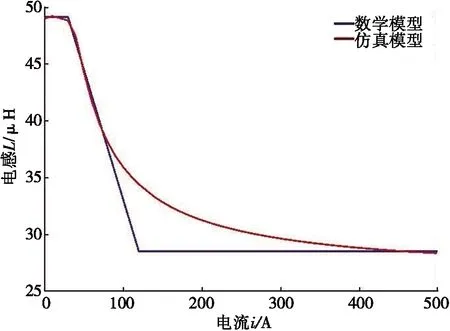
2 基于平板磁芯的WPT系统传输性能分析

3 基于平板磁芯的WPT系统的控制
3.1 自适应控制理论
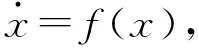


3.2 基于平板磁芯的WPT系统自适应控制

4 结束语
