转向紧急避撞轨迹规划与模型预测跟踪控制
2020-06-09姜顺明吴陶然匡志豪
姜顺明,解 建,吴陶然,匡志豪,周 涛
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
0 引言
目前,车辆的主动避撞多采用自动紧急制动系统。然而,制动距离与车速成二次增长关系,而转向时纵向行驶距离与车速近似成线性关系[1-2]。随着车速的增加,制动避撞潜力下降,转向避撞潜力上升。当车速高于某值,制动无法避撞时,转向仍可能躲避障碍,这为较高车速下的紧急避撞提供了一个有价值的选项。为此,转向紧急避撞成为智能车辆主动避撞的一个研究热点[3-5]。快速合理地进行轨迹规划以及在车辆稳定前提下准确地跟踪轨迹,是实现转向避撞功能的关键。
轨迹规划是智能车辆的一个重要研究领域[6-9],但多针对非紧急状态场合。人工势场法有较快的规划速度,但存在轨迹不连续、易产生局部最优解等问题。遗传算法与蚁群算法等智能优化算法的实时性难以保证,尤其是针对紧急工况下的转向避撞。紧急避撞轨迹规划的要求是可避开障碍、有利于保持车辆稳定以及快速实时。多项式规划法具有计算快、实时性好的特点,且轨迹的侧向速度与加速度变化连续平稳[10-11],但传统多项式法针对非紧急场合,缺乏对车辆稳定性因素的足够考虑。因此,本文提出一种限制侧向加速度的多项式轨迹规划方法,以利于提高转向避撞的车辆稳定性,以及满足规划算法的快速和实时性需求。
与经典控制、最优控制和鲁棒控制等控制方法相比,模型预测控制具有滚动优化、鲁棒性好和可反馈校正误差等优点[12-15]。本文在转向避撞轨迹跟踪中采用模型预测控制方法,基于3自由度车辆动力学方程建立预测模型,以车辆运动位置和车身横摆角跟踪误差最小作为控制目标,以前轮转角、前轮转角增量以及轮胎侧偏角作为约束,实现智能车辆在紧急转向避撞时准确跟踪规划轨迹,并保证车辆避撞的稳定性。
1 紧急避撞轨迹规划
采用多项式法进行紧急避撞轨迹规划,综合考虑轨迹规划效果和计算量,多项式次数选5。5次多项式轨迹纵向位置X和侧向位置Y与时间t的关系表达式分别为:
(1)
(2)
式(1)和式(2)中多项式系数可用向量形式表示:
a=[a0,a1,a2,a3,a4,a5]T;
(3)
b=[b0,b1,b2,b3,b4,b5]T,
(4)
a、b的求解方法为:
a=T-1Qx;
(5)
b=T-1Qy,
(6)
其中:
Qx=[X(t0),Vx(t0),Ax(t0),X(tf),Vx(tf),Ax(tf)];
Qy=[Y(t0),Vy(t0),Ay(t0),Y(tf),Vy(tf),Ay(tf)];
其中:t0为规划起始时间;tf为规划结束时间;Vx为纵向速度;Ax为纵向加速度;Vy为侧向速度;Ay为侧向加速度;X、Y分别为纵向位置和侧向位置。
完成轨迹规划需确定Qx和Qy中t0和tf的各个运动状态参数。图1为纵向车速与纵向末位置对侧向加速度的影响。假定车辆t0从图1a原点出发,规划时各运动状态参数的已知或限制条件如下:
避撞过程时间很短,纵向车速Vx基本不变,故Vx(t0)=Vx(tf),且Ax(t0)=Ax(tf)=0。
Y(t0)=0,并定义轨迹侧向位移ye=Y(tf)-Y(t0),其大小由智能车辆根据由感知系统得到的障碍与自车间的横向距离实时选择。ye选得过小,不能保证避开障碍;ye选得过大,可能越出车道,且会使车辆侧向加速度过大,失稳风险增加。因此,ye取1.9~3.7 m。
侧向初速度Vy(t0)、侧向末速度Vy(tf)、侧向初加速度Ay(t0)和侧向末加速度Ay(tf)均为0。
在以上条件下,式(2)可表示为:
(7)
对式(7)求二阶导数,得到侧向加速度:
(8)
侧向加速度是评价车辆稳定性的一个关键参量,在轨迹规划阶段就考虑限制侧向加速度有利于保证转向避撞的稳定性。由式(8)可知:纵向车速Vx以及纵向末位置X(tf)影响侧向加速度的大小。令纵向末位置不变,得到不同车速下,侧向加速度关于时间的变化曲线,见图1a。图1a中,每条曲线为固定车速下,车辆在整个轨迹跟踪中的理想侧向加速度。由图1a可知:纵向车速越大,车辆的侧向加速度越大,并且存在较高的峰值,这对车辆稳定是不利的。若令纵向车速不变,不同纵向末位置与侧向加速度有相似的规律。
根据式(8)可求出轨迹规划时间段内的侧向加速度峰值Ay max,它是关于Vx和X(tf)的一个函数:
Ay max=f[Vx,X(tf)]。
(9)
根据式(9)可以得到侧向加速度峰值与纵向车速、纵向末位置的关系图,如图1b所示。为了提高车辆转向避撞的稳定性,设置一个侧向加速度峰值的限值M。车速Vx可由智能车感知系统得到,再根据关系式f[Vx,X(tf)]=M,可确定一个纵向末位置X(tf)。至此,Qx和Qy中所有参数都已确定,即轨迹规划已完成。

(a) 侧向加速度关于时间的变化曲线
图1 纵向车速与纵向末位置对侧向加速度的影响
2 车辆动力学建模
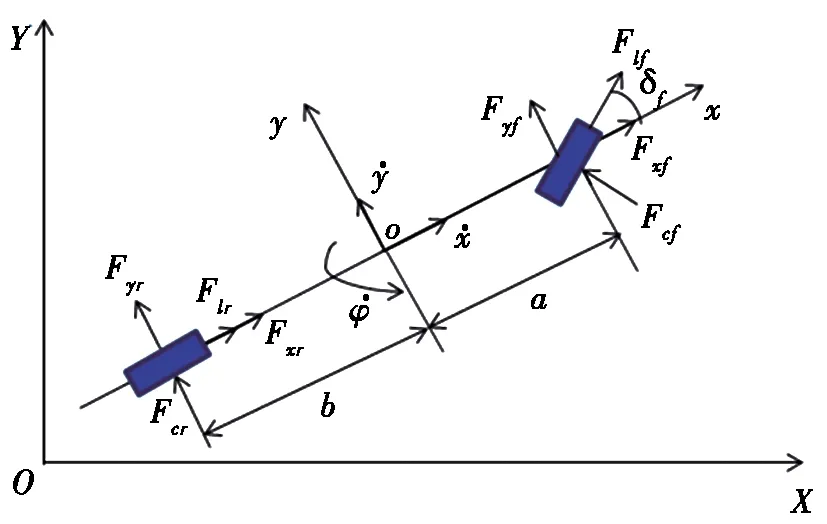
图2 3自由度车辆模型
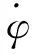
在x轴、y轴、z轴3个方向上的动力学方程为:
(10)
其中:Iz为车辆绕z轴的转动惯量;Fxf、Fxr、Fyf、Fyr为虚拟力,由轮胎纵向力与侧向力分别在x轴与y轴上的分力组成。采用Pacejka轮胎模型[16],得到前、后轮纵向力与侧向力:
(11)
其中:Clf、Clr分别为前、后轮胎纵向刚度;Ccf、Ccr分别为前、后轮胎侧偏刚度;sf、sr分别为前、后轮胎的滑移率。
将式(11)代入式(10),得到用于模型预测控制非线性的动力学模型:
(12)
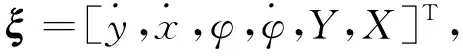

(13)

3 转向避撞模型预测控制
3.1 建立预测方程
对式(13)进行离散化处理得到:
ξ(k+1)=A(k)ξ(k)+B(k)u(k),
(14)
其中:A(k)=I+TA(t);B(k)=TB(t);T为采样周期;I为单位矩阵。
设定

(15)
则有

(16)

设预测时域为Np,控制时域为Nc,预测方程进一步写成:
W=ψkp(k|t|)+Θk△U(k),
(17)

3.2 目标函数设计
准确地跟踪规划轨迹的运动位置及车身横摆角是转向避撞的关键,故以车辆运动位置和车身横摆角跟踪误差最小化作为控制目标。定义系统输出量:
η=CW,
(18)

为实现车辆平稳地跟踪规划轨迹,防止前轮转角突变的危险情况,在目标函数中采用控制量的增量代替控制量,即采用前轮转角增量作为实际控制量,这样在每个控制周期,可将前轮转角限制在合理范围内,提高避撞的车辆稳定性。以前轮转角增量作为目标函数的控制量,控制目标函数表示为:
(19)
其中:ηref为规划轨迹的期望输出量;△u为前轮转角增量;Q和R为权重矩阵;ρ为权重系数;ε为松弛因子。
3.3 约束条件设计
为了保证避撞时车辆的稳定性,设计的约束包括前轮转角极限约束、前轮转角单位时间增量约束以及轮胎侧偏角约束。
在避撞轨迹跟踪过程中,控制器输出前轮转角值给转向执行机构,前轮转角及其增量约束应满足车辆前轮转角物理极限值,同时考虑避免车辆在较高速下转向过度的失稳危险,取前轮转角及其增量约束为:-15°<δ<15°,-0.4°<△δ<0.4°。
车辆动力学模型在线性化处理过程中,各个角度做了小角度的假设。另外,当轮胎侧偏角小于5°时,轮胎侧向力与侧偏角近似成线性关系。综上考虑,将前轮侧偏角约束值限定为:-3°<α<3°。
4 控制结果与分析
采用Carsim与Simulink软件进行联合仿真,在Carsim软件中建立整车模型,模型预测控制算法用m语言写入Simulink软件的S函数中作为控制器,输出控制变量给Carsim车辆模型进行执行。车辆主要参数为:整车质量1 723 kg,质心与前轴间距1.23 m,质心与后轴间距1.47 m,车身转动惯量2 550.3 kg·m2,预测时域15个采样周期,控制时域5个采样周期。轨迹规划时侧向位移选择2.0 m,侧向加速度峰值的限值为0.28g。

图3 制动和转向所需纵向安全距离
首先,计算各个车速下制动和转向所需纵向安全距离,如图3所示。由图3可知:当车速高于56.2 km/h时,制动避撞所需距离大于转向避撞所需距离。为验证多约束模型预测控制(model predictive control with multi-constrains,MMPC)轨迹跟踪能力,分别以60 km/h、70 km/h和80 km/h的车速进行轨迹规划和跟踪控制,结果如图4所示。
车速为60 km/h、70 km/h、80 km/h时轨迹跟踪规律相似,以80 km/h为例进行分析。80 km/h车速下的轨迹跟踪效果如图4a所示。由图4a可知: 车辆在整个避撞过程中均能较好跟踪规划轨迹,仅在第2次转向时出现超调量。由图4b可知: 最大超调量随车速的增加而增加,在80 km/h时仅为0.23 m,相较于车身宽度和道路宽度基本可以忽略。
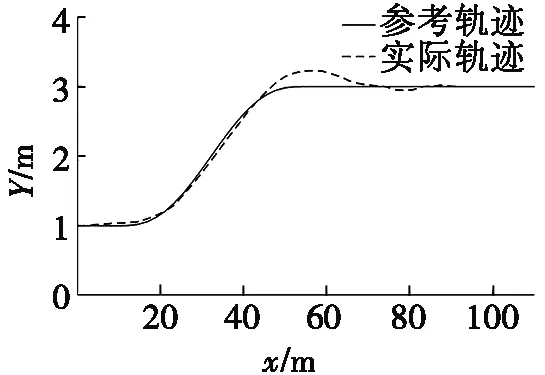
(a) 80 km/h车速下的轨迹跟踪效果

(b) 横向位置跟踪误差

(c) 前轮转角
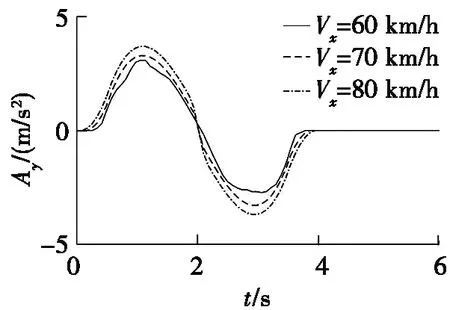
(d) 侧向加速度
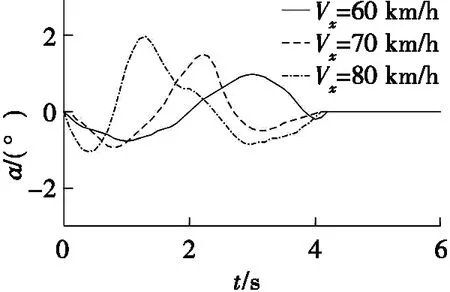
(e) 轮胎侧偏角
图4 MMPC轨迹跟踪性能
由图4c可知:自车在不同车速下,其前轮转角均在实际车辆前轮转角物理极限范围内,整个变道过程中前轮转角变化较平稳,无明显阶跃。随着车速的增加,前轮最大转角增大,80 km/h时仅比60 km/h时增大了0.3°。由于模型预测控制存在预测时域,对车辆的控制会出现超前或滞后现象,使得自车在转向避撞开始之前和结束之后有较小的前轮转角,但总体跟踪效果较理想。
由图4d可以看出:侧向加速度变化较平稳。随着车速的增加,侧向加速度的峰值也在增加,虽然在峰值时超过了轨迹规划时的预设值0.28g,但始终不超过0.40g,符合Pacejka轮胎模型的拟合要求,预测模型精度准确。由图4e可知: 随着自车车速的变化,轮胎侧偏角始终在侧偏角约束范围内,保证了车辆在转向避撞过程中的稳定性。
忽略目标函数中轮胎侧偏角因素,忽略约束条件中对轮胎侧偏角和前轮转角的限制,构建前轮转角增量单约束模型预测控制(model predictive control with single constrain,SMPC),与MMPC进行对比。仿真中,设定在80 km/h车速下对相同轨迹进行跟踪,结果如图5所示。
由图5a可以看出:SMPC和MMPC在第1次转向时均能跟踪轨迹,但SMPC在第2次转向时发生了较大的偏差,最大误差达到了1.1 m,相对于避撞宽度不可接受,并且由于误差过大,车辆逐渐失去了轨迹跟踪能力,发生车道偏离。MMPC在振荡后消除了误差,完成了转向避撞。由图5b可知:在开始阶段,SMPC的轮胎侧偏角处在约束值3°以内,车辆处于可控状态,随后车辆发生严重侧滑,侧偏角超过设定,车辆失控,在MMPC完成避撞动作后,SMPC依然存在3°左右的侧偏角,车辆处在不稳定状态。

(a) 轨迹跟踪效果
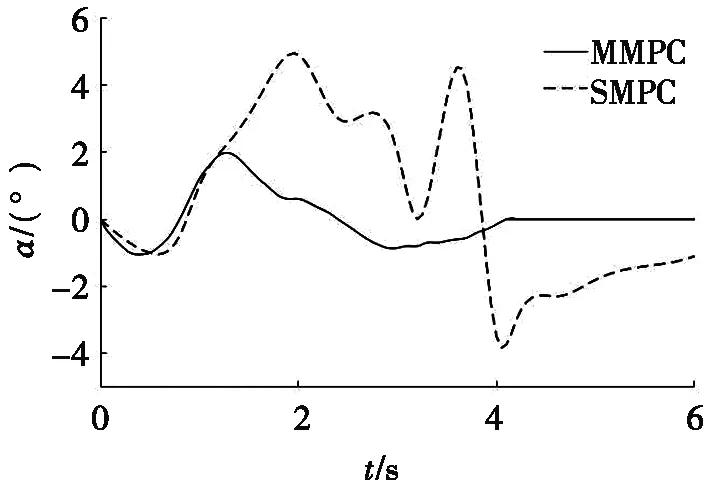
(b) 轮胎侧偏角
图5Vx=80 km/h时,MMPC与SMPC轨迹跟踪对比
5 结束语
基于五次多项式设计转向紧急避撞轨迹,提出根据一定限值下侧向加速度峰值方程式来确定各种车速时的轨迹纵向末位置。该方法得到的避撞轨迹平滑连续,易快速实现,有利于保持避撞车辆的稳定性。
采用多约束模型预测控制来跟踪转向避撞规划轨迹,控制目标是准确跟踪轨迹的运动位置和车身横摆角,设计了针对前轮转角、前轮转角增量和轮胎侧偏角的约束条件。60 km/h、70 km/h和80 km/h车速下的控制结果显示,横向位置跟踪误差小,跟踪效果较理想,跟踪过程中的侧向加速度和车轮侧偏角始终在安全范围内,保证了转向避撞的轨迹跟踪性能以及车辆稳定性。
