方程思想在初中几何中的运用

吴春红

【摘  要】初中阶段所涉及的各种知识点中都有方程思想的影子，方程思想从本质上说是一种同代数相关的思想，因此部分几何问题似乎同方程思想没有联系，不过在解决这类问题的过程中人们往往发现没有方程思想的参与是行不通的。所以，教师应培养学生掌握问题中“隐形”条件并借助此类条件对数学问题加以解决的能力，也就是要培养学生将方程思想运用于各类数学问题解决的能力。本文就方程思想在初中几何中的运用做了一点探索。

【关键词】方程思想;几何;运用

中图分类号：G633.63      文献标识码：A      文章编号：0493-2099（2020）35-0141-02

The Application of Equation Thought in Junior Middle School Geometry

（Xiting Junior High School， Tongzhou District， Nantong City， Jiangsu Province，China）WU Chunhong

【Abstract】The various knowledge points involved in the junior high school stage have the shadow of equation thinking. Equation thinking is essentially a kind of algebra-related thinking. Therefore， some geometric problems seem to have no connection with equation thinking， but they are solving such problems. In the process， people often find that the participation without equation thought is not feasible. Therefore， teachers should cultivate students' ability to master the "invisible" conditions in problems and use such conditions to solve mathematical problems， that is， to cultivate students' ability to apply equation thinking to solving various mathematical problems. This article does a little exploration on the application of equation thinking in junior high school geometry.

【Keywords】Thoughts of equation;Geometry; Application

一、初中几何知识概况

在初中数学学科中，方程思想是始终涉及其中的，初中阶段几何教学中的知识点主要涉及针对三角形、圆形以及四边形的求解。具体来说，初中阶段能应用的方程内容主要包括一元一次以及二元一次方程或方程组，同时也可能用到分式方程，一元二次方程也是解决初中问题时候会用到的方程内容。其中一元一次方程就是只包含一个未知数，其最高次数是1，同时等号两边均是整式的等式形式，这种方程的根的数量只有一个;如果一个一元方程，其中所包含的未知数数量只有一个，同时未知数项其最高次数为2，而方程又为整式方程，那么可以称其为一元二次方程;包含两个未知数，同时这些未知数它们的项的次数均为1，这样的一种整式方程就称为二元一次方程;分式方程属于方程的一种，这是一类有理方程，其分母中包含未知数或是未知数整式。

二、如何将方程思想应用在初中几何教学活动中

方程思想为初中阶段所学的代数知识中包含的核心思想，在整体初中代数学习内容中都有它的身影，可见它同初中代数之间的密切联系，然而，这并不意味着这种思想同初中几何之间就没有什么联系。初中教学所使用教材也指出这样一个事实，即方程是一种可以有效地将现实世界里存在的各种数量关系体现出来的数学模型，因此方程思想不光在代数问题的解决上有很广泛的应用，同时也可以用来解决很多几何领域的问题，具体来说就是借助图形所具有的一些形式建立方程，再通过方程解析找到答案。实际上，对于求解初中几何问题甚至是一切几何问题来说，方程思想都是一种重要的手段。

三、用方程思想解决初中几何问题常见的几个切入点

用方程思想解决初中几何问题常用的模式主要有六种，第一种是借由多边形内角和公式建立方程，很多同多边形相关的问题都是给出内角和度数，要求求边数，这个时候在这一公式基础上建立方程，再解方程就比较容易得到多边形边数;第二种是借由相似三角形具有的性质来建立方程，由于这类三角形对应边彼此成比例， 因此在解决相关的问题时经常要利用该性质在方程和几何之间形成联系，以解决有关问题;第三种是借由勾股定理建立方程，该定理不光在数学领域非常关键，而且也同现实生产生活有较为密切的联系;第四种是借由面积关系来建立方程，有些几何问题如果通过面积关系基础上建立的方程分析就会容易找到答案;第五种是借由三角函数来建立方程，该函数同数学学科和现实生活之间也具有重要的联系，特别适合解决测量方面的问题;第六种是借由圆的性质来建立方程，圆相关性质结合方程思想可以用来解决多种多样的问题。

四、利用方程思想解决初中几何問题的方案示范

（一）平面几何中的折叠问题

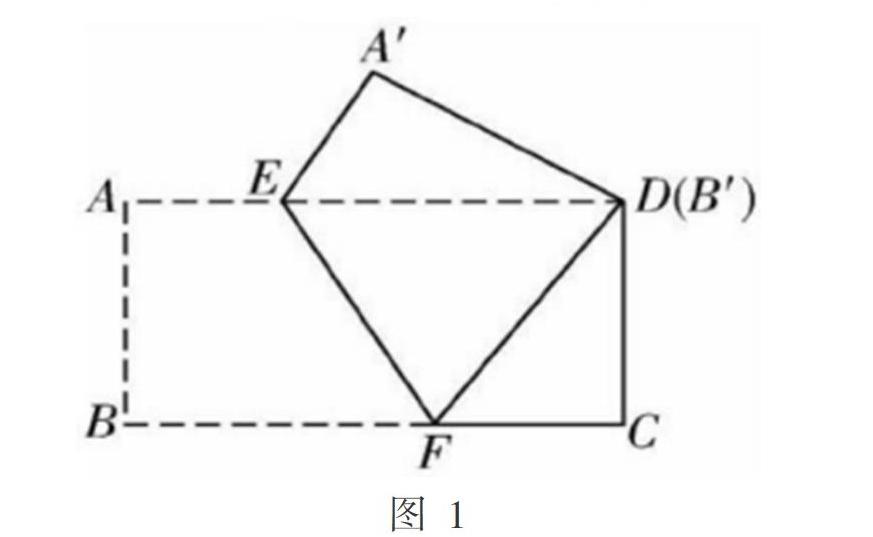
初中阶段的几何学习涉及平面几何的内容，其中的折叠问题比较具有代表性，除了线段及三角形几何形状的折叠之外，四边形折叠也是其中一种，这类折叠问题很多都可以通过方程思想来求解。例如人教版数学教材八年级下册中包含四边形的内容，这里就通过利用几何思想解决四边形折叠问题来一窥究竟。例：将矩形纸板[ABCD]根据图1中给出的方式进行折叠，让顶点[B]与点[D]互相重合，以EF作为折痕，假如[AB]长度为[6cm]，[BC]长度为[=10cm]，那么[DF]長度是多少，重叠部分△DEF其面积又是多少？

解题思路：设[DF]长度是[xcm]，则[CF]长度为（[8-x]）[cm]，通过勾股定理解得[x=7.5cm]，在此基础上就能继续求解，最终可以获得[△DEF]这个重叠部分的面积。通过本题的解题方案可以发现，试图对几何问题进行解决的时候，如果能基于图形本身的性质合理建立方程或方程组，并利用解方程的方法探索答案，解题就变得更容易了，所以利用方程思想处理这些问题应，成为初中生需要掌握的一种能力和技巧。

（二）利用方程思想解决平面几何中函数及几何图形类问题

利用方程思想还可以解决平面几何中函数及几何图形方面问题，此类问题中比较常见的关系主要包括函数同三角形之间的关系、函数同四边形之间的关系以及函数同圆之间的关系，在解决涉及这些内容的问题过程中都可以将方程思想运用进来。例如，在平面直角坐标系里面有一个直角梯形[OABC]，[AB]平行于[OC]，[OA]长度是5，[AB]长度是10，[OC]长度是12，[y=ax2+bx]这一抛物线经过两点[B]和[C]。（1）请将抛物线解析式算出来;（2）有一动点，假设是P，P从点A开始出发，并沿着[AC]朝点[C]方向前进，速度为两个单位长度/s，与此同时，另有一个动点，假设是[Q]，[Q]从点[C]开始出发，并沿着[CO]朝点O前进，速度为一个单位长度[/s]，一旦[P]前进到点[C]，则两点在同一时间停止运动，运动时间设为[T]秒，那么[T]的值是多少的时候[△PQC]构成直角三角形？

针对第一个问题，首先，根据0A、AB以及OC的长度值可以知道B点坐标为（10，5），C点坐标为（12，0），在此基础上将a、b的值计算出来，最终得到抛物线的解析式。针对第二个问题，首先还是使用勾股定理计算出AC长度为13，在此基础上首先根据已知条件计算出点P前进到点C花费的时间为6.5秒，那么CP的长度值为AC长度减去AP长度的差值，CQ=T，将角PQC为直角以及角CPQ为直角两种可能情况都考虑进去，就可以计算出当T的值是多少的时候，该三角形构成直角三角形。在解决该问题的时候，初中几何中涉及的相似问题以及函数内容和方程思想形成了有机的结合，这样学生不光可以深化对相关函数知识的理解，还可以提高逻辑思考能力。

五、结语

在初中几何学习中，初中数学教师应在充分认识到方程思想对学生几何学习的积极意义的基础上带领学生对其进行应用，这样不光能让学生更有能力解决一些几何问题，也能让学生学会一种新的解决问题的思考途径。

参考文献：

[1]孙玉勇.浅析中学几何解题中蕴含的方程思想[J].数学学习与研究，2014（07）.

（责任编辑  袁  霜）