长江航运景气指数预测模型构建与分析
2020-06-08李慧冯新双
李慧 冯新双
摘 要:长江航运景气指数作为长江航运市场主要监测手段之一,能反映和预测长江航运的宏观经济发展状况及其变化的过程。分析预测长江航运景气指数,有助于长江航运宏观经济政策的制定和实施。以长江航运景气指数为对象,使用指数平滑模型、多项式拟合函数模型、BP-GA模型分别对景气指数进行建模分析,结果表明将指数平滑模型与BP-GA模型结合,能更加准确预测长江航运景气指数在时间序列上的变化趋势,预测拟合度最佳。最后以该模型预测分析2020年1季度至4季度的景气指数值,为未来长江航运发展提供参考。
关键词:长江航运;景气指数;预测模型
近年来,长江航运快速发展,新时期长江经济带高质量发展对长江航运市场监测和宏观调控提出了更高的要求。长江航运景气指数作为市场监测体系里的重要组成部分,可视化地反映长江航运市场运行质量和趋势变化,影响政府部门对长江航运宏观调控的准确把握。同时长江航运景气指数作为长江航运市场主要监测手段之一,发挥了信息引导、预警管理作用,准确预测景气指数,一定程度上可以避免航运市场大起大落,对預判经济发展趋势,促进长江航运市场健康持续发展具有重要的意义。因此,有必要针对航运市场的景气指数预测开展专门研究,科学把握发展的态势和对于未来长江航运发展做出指导,以满足长江航运高质量发展的需要。
在景气指数预测方面已有相关研究,例如孙颖通过构建ARIMA模型对我国物流业景气指数进行预测[1];朱东红等人使用GM(1,1)预测、BP 神经网络预测和ARIMA预测三种模型对物流景气指数进行建模分析,并选择最适合的预测模型[2];另外,在房地产行业、工业、服务业等景气指数预测方面也有较多研究[3-6]。我国航运发展正处于由航运大国向航运强国转变的阶段,在航运方面也逐步开展了相关的景气指数研究和应用,例如,从企业角度反映航运发展情况的中国航运景气指数(CSPI)[7],侧重于反映航运企业经营以及航运市场动态情况的宁波航运经济指数(NSEI)等,但对于航运景气指数预测的研究相对较少,尤其是针对长江航运的景气指数,缺乏定量分析以及预测参考,因此需要进行更深一步的研究。景气指数预测方法较多,比如温特线性与季节性指数平滑法、自适应过滤法和ARIMA模型拟合法等,本文主要利用Matlab和Excel工具,探究更适合长江航运景气指数的预测模型。
1 预测模型分析
通过长江航务管理局官网发布的长江航运景气指数调查报告,收集了2012—2019年的数据,并进行预测分析。
1.1 指数平滑预测
指数平滑法是生产预测中常用的一种方法,也用于中短期经济发展趋势预测。它是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测,其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。Excel预测工作表其实是基于函数指数平滑函数(FORECAST.ETS)实现的,该函数原理是通过使用指数平滑 (ETS) 算法的 AAA 版本计算或预测基于现有(历史)值得出的未来值。程序代码为:
其中:target_date(目标日期)指向要预测值的数据点。目标日期可以是日期/时间或数字。values(值)指要预测下一个点的历史值。timeline(时间线)指日期或数值数据的独立数组或范围。时间线中的值之间必须具有一致步长,不能为零。seasonality(季节性)指表示季节性的数值。data_completion(数据完成功能)指尽管时间线需要数据点之间的固定步长,但是 Forecast_ETS 支持多达 30% 的缺少数据,并会自动对其进行调整。aggregation(聚合)指尽管时间线需要数据点之间的固定步长,但是 Forecast_ETS 聚合具有相同时间戳的多个点。
根据指数平滑法,基于2012-2018年数据进行预测,得出2019年景气指数预测数据,并与实际值比较,如表1和图1所示。
1.2 多项式拟合预测
对于给定的一组数据( )(0,1,2…),求作n次多项式( )
使其满足
利用Matlab软件进行拟合函数编程,画出拟合曲线如下图所示。
并得出拟合的曲线方程如下:
拟合函数是以 为自变量的多项式函数,将时间序列转换为数值形式而构建相应的拟合函数,根据拟合函数可以得出特定 值下的 值,即可进行预测。该方法不适用于景气指数的预测,根据图2可知,拟合值与实际值误差较大,曲线趋势与实际变化趋势有所出入,并且将时间转换为数值形式将导致随着时间 的增加, 值整体趋势将不断增加。因此,多项式拟合预测不适宜作为长江航运景气指数预测模型。
1.3 BP-GA预测模型
BP-GA算法是将神经网络与遗传算法两者结合,通过遗传算法优化神经网络的过程。利用遗传算法对所构建神经网络的权值及阈值进行优化,再将最优的初始权值及阈值赋给神经网络,由此得到优化后的神经网络,从而利用该网络进行训练和预测,使得预测结果更为精确。长江航运景气指数按照企业类型可划分为港口企业景气指数和航运企业景气指数,可根据港口与航运企业景气指数数据预测综合的景气指数。本文利用Matlab软件进行程序的编写以及算法分析。
1.3.1 BP神经网络
BP神经网络结构由输入层、隐含层及输出层构成。将港口企业景气指数和航运企业景气指数作为输入层,将长江航运景气指数作为输出层,故输入层节点数为2,输出层节点数为1。隐含层节点数可根据如下公式进行确定:
1.3.2 遗传算法(GA)
遗传算法是指模拟生物进化期间的自然选择和遗传学原理,从而寻找最优解的方法。包括种群初始化、适应度函数的确定、选择、交叉及变异操作。其中,对于神经网络初始权值、阈值的优化,其个体适应度值是指神经网络预测与期望输出值两者之间所产生的误差绝对值的和,即:
式中,n表示网络输出节点数; 和 分别表示网络第i个节点的期望输出和预测输出值;k为系数。对于选择操作,本文运用轮盘赌法,计算过程为:
式中, 表示个体i的适应度值,对于两次遗传算法优化,都需要个体适应度值越小越好,故在个体选择操作前需对适应度值求倒;k为系数;N表示种群个体数目。
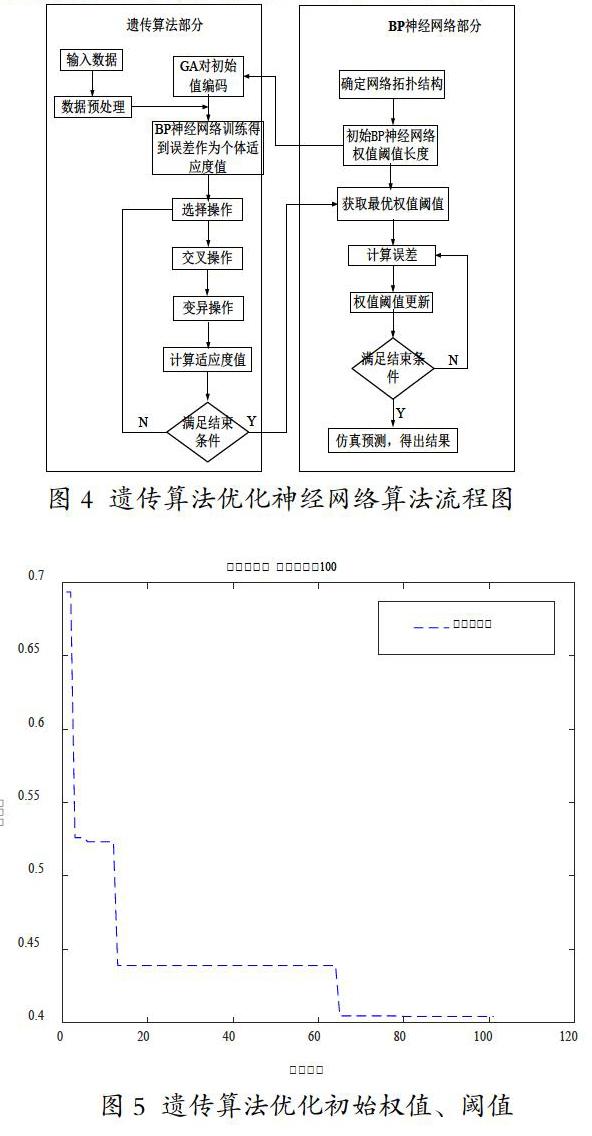
1.3.3 遗传算法优化神经网络
遺传算法优化神经网络主要包括确定网络结构、优化网络和神经网络预测三个部分。
本文神经网络有2个输入,1个输出,取隐含层节点数为5,故采用2-5-1的神经网络结构。
神经网络优化的算法流程如图4所示。
1.3.4 BP-GA预测
BP神经网络输入神经元2个,隐层神经元5个,输出神经元1个,训练函数使用trainlm函数,训练均方差目标为10-5,学习效率为0.01,总步数为100。遗传算法采取实数编码,初始种群规模数为10,进化次数为100次。经过约70代的遗传,算法找到最优的权值和阈值。
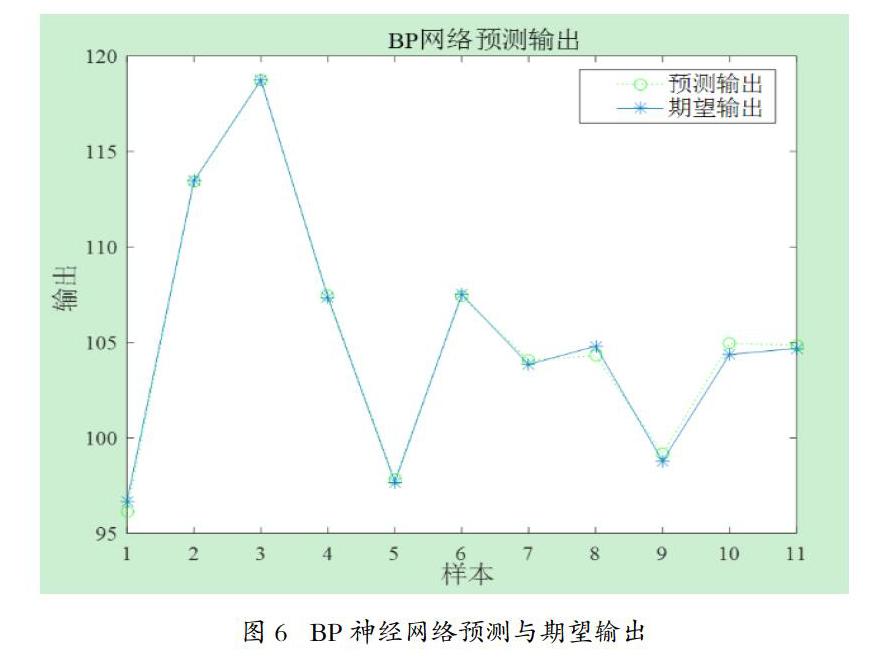
最优的网络状态下,11组测试数据的预测输出和期望输出结果如图6所示,误差非常小,说明经过遗传算法优化得到最优的神经网络权值和阈值后,将最优的值赋予神经网络,经过优化后的 BP神经网络响应面模型比较精准,可用于更为精确的预测。
2 模型比较与预测
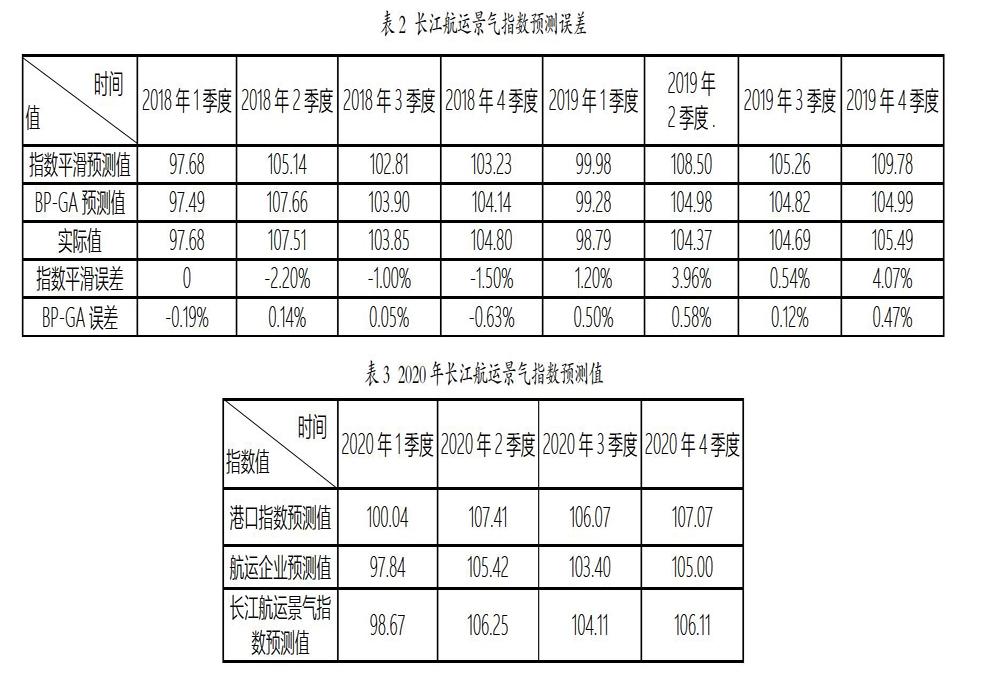
根据分析,多项式拟合预测方法不适宜长江航运景气指数预测,比较指数平滑法和BP-GA法,如表2所示。
由表2可知,两种预测方法误差均较小,由于长江航运景气指数具有一定的季节性,两种方法相比,利用港口企业景气指数和航运企业景气指数作为输入值综合预测长江航运景气指数的BP-GA模型预测结果更为准确。因此,可将两种方法结合,通过指数平滑法预测出港口和航运企业的景气指数,再通过BP-GA算法预测出最终的长江航运景气指数,使其更加精准的反映景气变化趋势。利用该模型,预测2020年1季度至4季度的长江航运景气指数如表3所示。
长江航运景气指数99-101为临界区,125点以上为良好景气区,75点以下为深度不景气区。故2020年1季度处于不景气区,2季度至4季度均可望处于景气区。
由于2020年受新冠肺炎疫情影响,航运业遭受巨大打击,尤其是2020年一季度,大部分企业停工停产,3月才逐步恢复,业绩面临断崖式下滑,经营受到严峻挑战。新冠肺炎疫情属于非季节性的突发因素,而预测模型无法将此突发因素考虑在内,故考虑新冠肺炎疫情影响,2020年1季度至4季度长江航运景气指数在预测结果的基础上,将进一步下滑,整体变化趋势仍呈震荡格局。
3 结论分析
本文通过统计2012年1季度到2019年4季度的长江航运景气指数以及各细分类别数据,利用指数平滑模型、多项式拟合函数模型、BP-GA模型对原始数据进行拟合,通过误差和分布图分析得到最佳预测模型,即通过指数平滑法预测出港口和航运企业的景气指数,再通过BP-GA算法预测出最终的长江航运景气指数,使其更加精准的反映景气变化趋势。
利用最优预测模型预测结果表明,2020年长江航运景气指数呈震荡格局,1季度景气指数位于最低谷,2季度之后将出现回升状态,并在2季度出现峰值。
参考文献:
[1] 孙颖.我国物流业景气指数的ARMA模型构建与预测研究[J].齐齐哈尔大学学报(哲学社会科学版),2017,(5):71-73.
[2] 朱东红, 钱叶霞, 陈东清.我国物流景气指数(LPI)预测模型的构建及分析[J]. 物流技术, 2019, 38(1): 88-93.
[3] 李星. 中国工业景气指数的预测研究[J]. 广东商学院学报, 2012, (3): 19-24.
[4] 张玉霞. 我国服务业景气监测预警研究[D]. 河北: 河北经贸大学, 2013.
[5] 陈志朋. 铁路移动设备景气指数研究[D]. 北京: 北京交通大学, 2014.
[6] 祝煦, 贺磊, 彭炎亮. 芜湖市房地产行业景气指数建模与预测研究[J]. 阜阳师范学院学报(自然科学版) , 2014,31(4):15-21.
[7] 周德全, 真虹. 基于中国航运景气指数的中国航运业发展趋势[J].水运管理, 2010, 32(03):11-13.
