面向物联网业务绿色接入的异构蜂窝网络优化

刘娅汐，皇甫伟

北京科技大学计算机与通信工程学院，北京 100083

近年随着信息技术的飞速发展，赛博空间（Cyberspace）使能的新业务不断涌现.[1]作为联系物理空间和赛博空间的桥梁，物联网（Internet of things）[2]是诸多赛博使能（Cyber-enabled）业务的重要底层支撑平台. 在物联网数据的诸多接入和传输方式中，蜂窝网络（Cellular network）是最关键的技术之一，尤其在广域覆盖方面具有不可替代的价值[3]. 物联网终端可以基于多种方式接入蜂窝网络，如NBIoT（Narrow band internet of things）[4]和第五代移动通信技术（The fifth generation, 5G）[5].考虑到物联网设备数量庞大且广泛分布于所部署区域，基于异构蜂窝架构的移动通信网络可以通过宏基站和小基站的协同实现对部署区域更为广泛的覆盖，从而更好地支持物联网业务. 在目前和未来的移动通信网络发展中，物联网业务均受到了广泛的关注[6]. 值得注意的是，由于无线通信是通信网络耗能的主要方面，绿色通信（Green communication）也得到了学界的日益重视，在网络规划中满足广域物联网业务覆盖率要求的条件下最小化基站下行功率是一类重要且具有挑战性的难题[7].

物联网业务通常需要满足通信带宽和数据延时等要求，这些需求在网络性能分析模型中均可归结为若干射频信号层面的指标，其中最基础的是参考信号接收功率（Reference signal receiving power, RSRP）[8]和信号与干扰加噪声比（Signal to interference plus noise ratio, SINR）[9]. 若某个地理位置的信号达到门限要求则称该位置满足覆盖条件. 对网络运营商而言，在蜂窝网络的服务区域中，需保证服务范围内满足覆盖条件的面积达到一定的覆盖比例要求.

在网络规划及运维阶段中可调参数主要是天线的下倾角[10]和下行功率[11]等. 绿色通信需要降低基站的下行发射信号功率，而区域内大量终端的覆盖则通常要求基站发射信号功率足够大. 因此，满足下行信道覆盖率的条件下最小化基站发射总下行功率是一个典型的工程优化问题，目前主要的方法包括贪婪算法、穷举法、元启发式算法与梯度下降方法等. Tabia等[12]使用贪婪算法调节下倾角和频率优化下行覆盖率指标. 贪婪算法收敛速度快，但得到的可行解并不总是全局最优的. 为了获得全局最优解，Klessig等[13]使用穷举法通过调节基站天线的下倾角来最大化网络的覆盖率和容量. Gao等[14]使用了一种搜索全部基站天线下倾角和下行功率组合的穷举法进行网络优化. 穷举法可以得到最优化问题的全局最优解，然而计算复杂度非常高. 为了权衡可行解的质量和算法的计算复杂度，学者们也引入了元启发式算法. Han等[15]使用蚁群算法寻找下行功率的最优解. 为了减少覆盖空洞，Yin等[16]使用遗传算法通过不断优化天线的下倾角来解决扇区的损耗补偿问题. Valavanis等[17]阐述了覆盖率和容量优化模型并使用多目标遗传算法优化了天线方向角、3 dB带宽和下行功率. Balasubramany与Lampe[18]设计了一个基于模拟退火算法的覆盖率和容量优化机制，该机制通过联合调整天线电子下倾角和下行功率来实现. Phan等[19]提出了使用粒子群算法来调节天线下倾角进而实现网络覆盖优化. Sousa等[20]提出了多目标粒子群算法，通过调节天线下倾角和天线方向角来最优化覆盖率和干扰. 值得注意的是，上述方法中均未利用优化目标的梯度信息. 梯度方法的优化方向为目标函数值最快速的下降（反）方向. 基于梯度的方法通常可以达到更高的收敛速度. Liu等使用梯度下降算法通过优化天线方向角和下倾角来最大化网络覆盖率[21]和优化网络功率[22]，在算法收敛速度上超过了现有的不依赖梯度的其他算法，然而其主要针对宏基站部署情况，尚未讨论异构蜂窝网络场景，且梯度下降在优化过程中易出现抖动情况.

本文通过联合调节宏基站的下倾角和下行功率以及小基站的下行功率，在满足覆盖一定比例的物联网终端的条件下，建立了最小化网络发射总下行功率的问题模型和算法. 通过罚函数方法转化了原始的约束优化问题，并提出了一种基于优化目标平滑近似和均方根传播策略的梯度下降算法（Smooth-based gradient descent with RMSProp,SGR），该算法一方面通过函数平滑技术求解了不可导的目标函数并利用其次梯度信息，另一方面采用均方根传播（Root mean square propagation,RMSProp）[23]方法改善了算法的收敛性能. 通过实验可知，在物联网的低能耗数据接入网络优化中，本文所提出的算法具有良好的性能.

1 系统模型

假设在异构蜂窝网络的部署区域R 内有NM个宏基站第i个宏基站上安装了pi部天线此处pi≥1且1≤i≤NM，通常有pi=3. 同时，区域R 内也部署着NS个小基站每个小基站上安装一部全向天线.为评估覆盖率，部署区R内选J个采样点s1,s2,...,sJ. 这些采样点可以均匀分布于所部署区域，也可以根据赛博业务的地理分布进行选取. 网络部署如图1所示.

图 1 网络部署图Fig.1 Network deployment

采样点sj接收到的宏基站上天线的下行信号功率，dBm：

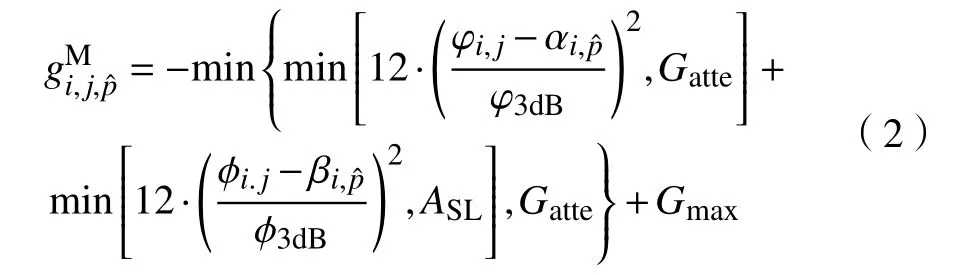
其中，函数min(x,y)返回x和y中的最小值；φ3dB和ϕ3dB分别为水平和垂直的半功率波束宽度，°；Gatte为最大天线回响增益，dB；ASL为天线辐射边带增益，dB；Gmax为 天线的最大增益，dB；分别为天线的方向角和下倾角，°. φi,j=arctan分别为相对采样点sj天线的垂直角度和水平角度，°. 其中为宏基站的挂高，m；为采样点sj的高度，m；为采样点sj与宏基站之间的欧式距离，分别为采样点sj与宏基站的位置坐标，m. 采样点sj接收到的来自小基站的信号功率，dBm：

采样点sj的RSRP表示接收到来自所有天线的信号功率的最大值，mW，可表示为

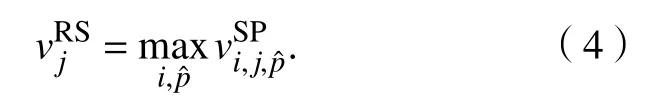
其中，Gau为服从高斯分布的背景噪声，mW. 此处考虑负载满载且不进行干扰抑制的恶劣条件. 设定分别为RSRP和SINR值的门限值，单位分别为dBm和dB. 则区域R 内的覆盖率Cov可表示如下：

其中，H(x)为阶跃函数，定义为自变量x≥0时，H(x)=1；反之H(x)=0. 区域R中所有基站的总下行功率，mW为：

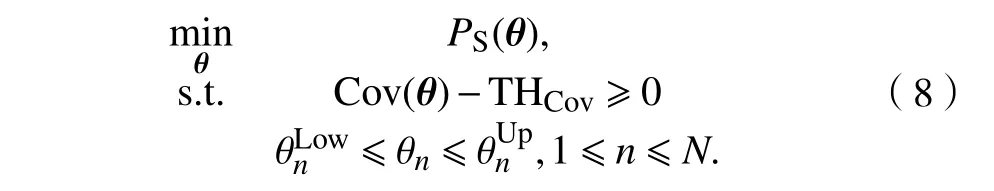
2 基于均方根传播的平滑化梯度下降

首先，式（8）是一个复杂条件约束下的优化问题，可首先运用罚函数方法将其转换为简单约束形式如下：

其中，λ为覆盖率的非负权重因子.Q(x)为保证约束条件Cov(θ)−THCov≥0成立的罚函数, 定义为Q(x)=min(0,x).

此时，优化目标函数L(θ)是关于可调参数的不可导函数. 为了利用梯度下降方法，需要对L(θ)进行平滑化，即利用与之近似但可导的函数替代它.

本文将最小值(函数min近似)替换为softmin(x1,···,xn)=−lne−cx1+···+e−cxn/c. 其中,c为较大的正常数，表明替换函数与原函数之间的近似程度，c越大则两者越接近. 类似的，将最大值函数替换为softmax(x1,x2,···,xn)=−softmin(−x1,−x2,···,−xn). 将阶跃函数H(x)替换为

此时，替换后的优化目标函数L(θ)关于可调参数是可导的，可以通过链式法则其各天线下行功率和下倾角进行求导，有

进一步可以根据链式法则逐步展开，以对下倾角的导数为例，有：

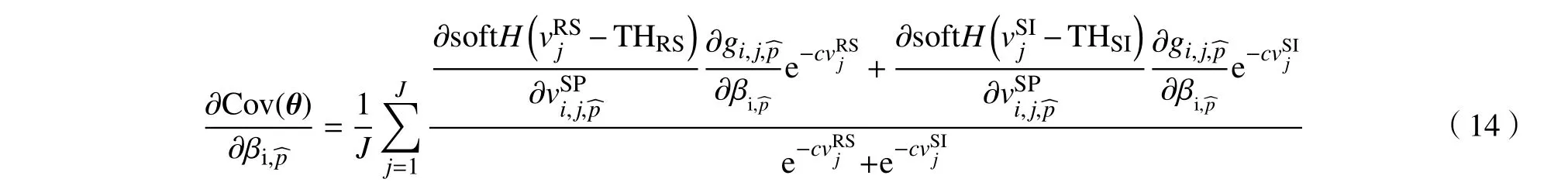
重复上述过程，最终可以得到目标函数关于各可调参数的闭式解形式的偏导数，从而获得梯度，此处1≤n≤N.

随后根据RMSProp加速方法[23]，本文提出了SGR算法，算法伪代码如下所示：

输入：初始可调参数θ={θ1,θ2,···,θN}及其他参数

输出：θ

3 仿真验证

本文拟在19扇区理想蜂窝场景下验证算法的准确性及性能，仿真场景如图2所示.

图 2 19扇区理想蜂窝仿真场景Fig.2 Simulation scenario of 19-cells ideal honeycomb

在图2中，宏基站分布在边长为300 m的正六边形蜂窝中点. 每个宏基站都安装了3部天线. 宏基站采用了集中化无线接入网络的架构. 小基站分布在部分六边形的顶点上，以模拟实际场景中弱覆盖区中的增补基站. 基站的挂高均为30 m.宏基站和小基站的下行功率可调范围分别为15～25 dBm和1～5 dBm. 宏基站天线下倾角的可调范围为0～10°. 假设该区域地形平坦. 宏基站上的3个天线的初始方向角分别设置为0°、120°和240°，天线初始下倾角设置为0°，下行功率初始设置为25 dBm. 小基站下行功率初始设置为3 dBm.图2中黄色圆点代表小基站上的全向天线，黄色扇形代表宏基站上的天线，其朝向对应天线方向角. 采样点均匀分布在部署区. 其余仿真参数如表1所示. 宏基站的路损使用COST-231模型[25]，可表示为

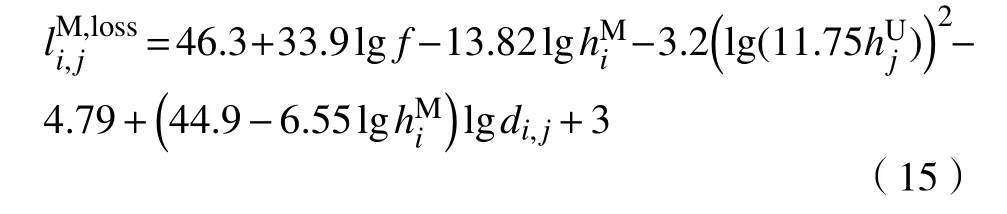
其中，f为工作频率，MHz. 仿真语言环境为Python 3.6，使用数学库Numpy 1.14.2及Numba 0.37等.

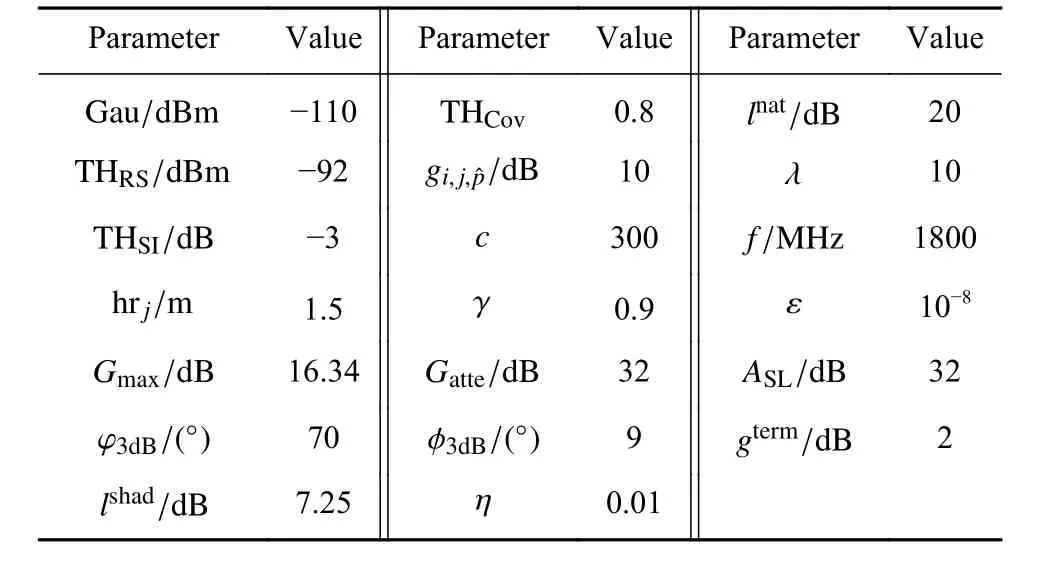
表 1 参数设置Table 1 Parameter settings

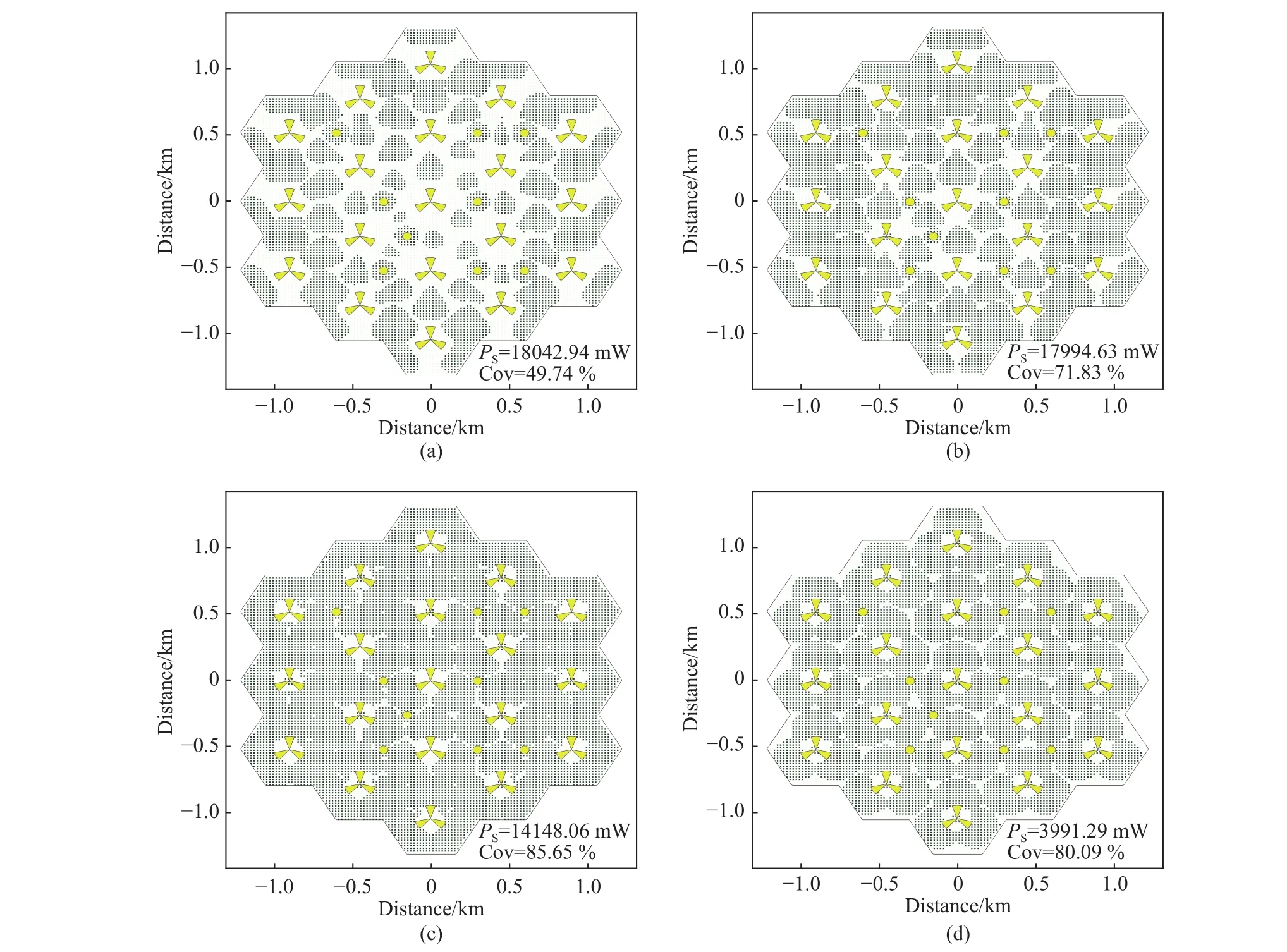
图 3 覆盖示意图. （a）初始状态（b）第1代（c）第100代（d）第1000代Fig.3 Illustration of coverage map: (a) initial state (b) the 1th iteration (c) the 100th iteration (d) the 1000th iteration

为了验证算法的准确性，图3给出了区域覆盖随迭代次数增加的变化示意图.

在每次迭代中，本算法计算一次目标函数的梯度，并根据梯度值进行一次参数更新. 图中深色区域代表覆盖的区域，白色区域代表未覆盖的区域. 由图3可以看出，随着迭代次数的增加，覆盖率逐步达到要求，下行总功率最终达到近优值. 具体优化过程说明如下. 初始情况下，部署区域的覆盖率不满足条件，即有Cov(θ)−THCov<0. 此时，在由原目标函数和罚函数组合构成的总优化目标中，梯度方向表明调整参数以提升覆盖率比降低下行总功率更为重要，因此在优化过程会优先提升覆盖率. 因此，覆盖率会逐渐上升，直到满足覆盖率条件Cov(θ)−THCov≥0. 当覆盖率满足时，罚函数为零，此时总目标函数以优化总下行功率消耗为主，在这一阶段中，总下行功率逐渐降低. 在此过程中，调整参数以降低下行功率可能会引起覆盖率的改变，甚至导致覆盖率再次不满足要求.当覆盖率降到门限以下时，优化过程仍将继续提升覆盖率，依次循环，直到覆盖率达到条件且总下行功率消耗趋于最小化. 图3（a）中给出了初始状态覆盖图；图3（b）给出了覆盖率处于上升阶段的覆盖图；3（c）给出了覆盖率超过门限但仍处下降状态的覆盖图；3（d）给出了下行功率稳定时的覆盖图.

为了进一步证明该算法的收敛速度，图4展示了覆盖率和总下行功率损耗与迭代次数的关系.图4（a）展示了梯度下降算法的优化过程，4（b）展示了使用RMSProp方法的梯度下降优化过程. 为了更清晰地展示优化初期覆盖率的上升情况，图4（c）展示了使用RMSProp方法的梯度下降优化前10代的局部过程. 对梯度下降算法，在初始阶段，由于覆盖率不满足约束，优化过程更倾向于提升覆盖率. 反之，在覆盖率满足约束时，优化过程则倾向于降低总下行功率损耗，通常会导致覆盖率降低. 上述过程反复进行，呈现出一种振荡的状态. 本文提出的基于RMSProp的梯度下降优化算法由于考虑了梯度的历史值，利用历史值进行了均方根传播，因此该算法的优化过程较为平滑，仅有少数次由于覆盖率不满足形成的小幅度跳跃，未出现反复的振荡. 梯度方法已经被证实为一种高效的最优化算法[17]，与缺乏梯度指导的其他算法相比，本文提出的算法在运行效率上有明显的优势.

4 结论

赛博空间和赛博空间使能业务已渗透到人类生活的诸多方面，在多个领域改变了人们的生活生产方式，尤其是物联网技术中心的蜂窝网络. 本文面向异构蜂窝中网络物联网业务的绿色接入问题，提出了一种基于平滑近似和RMSProp的梯度下降优化算法，通过使用罚函数将复杂约束的最小化总下行功率问题转化为简单约束的优化问题，并利用平滑近似将不可导的优化目标函数转化为可导的形式. 最后，使用RMSProp梯度下降算法解决了该优化问题.

本文在19扇区理想蜂窝场景下验证算法的有效性和效率，得到以下结论：

（1）在异构蜂窝网络中，本文提出的算法在优化覆盖率和下行总功率方面是有效的. 通过迭代过程的覆盖图可知，随着迭代次数的增加，覆盖率逐步达到要求，下行总功率最终达到近优值.

图 4 覆盖率和总下行功率损耗与迭代次数关系图. （a）梯度下降算法；（b）SGR算法前1000代；（c）SGR算法前10代Fig.4 Illustration of coverage and power consumption versus iteration:(a) gradient descent algorithm; (b) SGR algorithm with 1000 iterations;(c) SGR algorithm with 10 iterations

（2）本文提出的算法相比传统的梯度下降算法而言运行效率高，克服了传统梯度优化过程中容易产生的振荡问题，适合异构蜂窝网络场景和面向大规模网络场景的规划、部署和优化运维.

对于本文提出的基于平滑近似和RMSProp的梯度下降优化算法而言，虽然已经在理想蜂窝场景证明该算法的准确性和效率，但未来仍需在真实城市环境场景中验证该算法.