赛博空间中的天线散射特性研究

柴建忠，陈航宇，洪昊晖，钞 旭，赵京城✉

1) 航空工业第一飞机设计研究院, 西安 710089 2) 北京航空航天大学电子信息工程学院, 北京 100191

赛博空间（Cyberspace）现阶段主要指计算机及其网络中的虚拟现实（Virtual reality，VR），军事训练是VR应用最早、应用最多的领域[1]. 2000年之前，美国和中国就已经将VR应用于多兵种军事训练中. VR技术对于通信平台的性能提出很高的要求，传统4G网络已不能满足VR实时性的需求[2].5G网络可以满足VR技术需求[3]，5G核心技术主要包括大规模MIMO（Multiple-input multiple-output）天线阵列、超高密度网络等. 实际中放置大规模MIMO天线阵列的物理空间非常有限，互耦效应会大大降低香农容量[4]，天线间的互耦效应要被认真考虑[5-6]，在未来5G天线系统中,面临的最大挑战是如何有效消除阵列中单元天线间的互耦[7]. 针对MIMO天线阵互耦问题，可利用方位已知的校正源对天线阵列互耦进行校正[8-11]. 除校正方法之外，还可以利用缺陷地结构[12]、利用电磁带隙结构去耦[13]、利用寄生谐振单元法去耦[14]、利用去耦网络法去耦、利用中和线法去耦等，提高天线阵列的隔离度. 这些研究都在一定程度上降低了天线单元的互耦，或者降低了互耦对通信容量的影响，但是较少关注天线单元本身的散射特性. Kahn和Kurss[15]提出了最小散射天线的概念，当N个可触及的波导端口开路时，天线成为“不可见的”，这个概念对天线互耦特性研究有重要意义. 同样的天线辐射方向图，可能对应于多种不同形式的天线.而这些不同的天线，辐射特性相同，散射特性却有很大差别，选取低散射特性的天线单元对于降低大规模天线阵列的互耦是一个可行的研究方向.本文根据最小散射天线理论，研究单元天线散射机理，从而在大规模MIMO阵列天线设计时，选择有利于降低互耦的天线单元.

1 最小散射天线的散射矩阵

天线散射长期以来被分为模式项和结构项两大类[16-18]，这种分类方法有效分离了天线端口的失配反射，但是不能分离出由于天线形式不同引起的天线散射差别，分类不够细致，不利于工程应用. 根据最小散射天线理论，可将天线散射分成额外散射（Excess scattering）σI，伴随散射（Associated scattering）σII，失配散射（Mismatched scattering）σIII三个部分[19]. 最小散射天线是没有额外散射的天线，负载共轭匹配时，天线的总散射功率与接收功率相等.

Kahn提出最小散射天线的概念时，用到了四个假设条件：天线无损耗、可触端口无反射且无耦合、1～N端口开路和最小散射（与自由空间散射等效），由这四个条件，可以证明，规范的最小散射天线唯一的散射矩阵是

其中，Sβα为天线散射场对N个可触端口的散射矩阵，Iββ为无穷维单位矩阵，Sβα+为Sβα的共轭转置矩阵.

由于天线端口的开路状态并非端口直接断开，所以在应用该理论时有实际困难. 在微波传输线理论中，开路和短路状态密切相关. 根据最小散射理论，一个最小散射天线与一个透明的二端口网络串联，仍然为最小散射天线. 那么开路条件下的最小散射天线与一个四分之一波长的透明二端口网络串联，经推导可得新天线网络的散射矩阵为

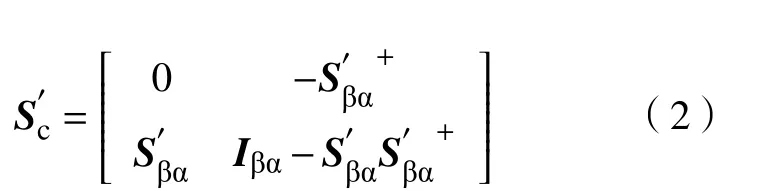
反射系数从1变为-1，正好符合网络端口的短路条件. 这也就证明了开路条件下的最小散射天线串联四分之一波长延迟线后，变为短路条件下的最小散射天线. 这一结论虽然简单，但是对于实际天线的最小散射实现却有重要意义，因为天线端口的开路并非端口直接断开，而短路却有很明确的实现状态.

2 X波段波纹喇叭天线散射的理论和实验研究

2.1 天线三部分散射从测量上分离的理论推导

一个波导端口波纹喇叭天线的结构示意图见图1.

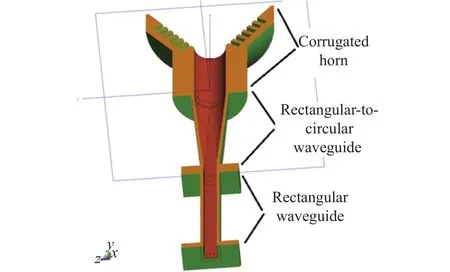
图 1 波纹喇叭天线结构示意图Fig.1 Structural sketch of a corrugated horn antenna

对于波纹喇叭天线而言，波纹喇叭本身和矩圆波导转换是必须的，直波导段根据连接需要选择适合的长度. 但是，对于天线散射来说，直波导段的长度会对散射场起到很大的影响. 如果忽略波导的衰减，直波导段可等效为透明网络处理，从而推导出波纹喇叭天线连接直波导后的散射矩阵为

单一平面波照射时，aγ=0，展开上面的矩阵，有

对测量来讲，关心的是b1和b2. 当天线在波导端口开路时，有a1=b1，代入式（4）中，可得

当天线在波导端口短路时，有a1=−b1，代入式（4）中，可得

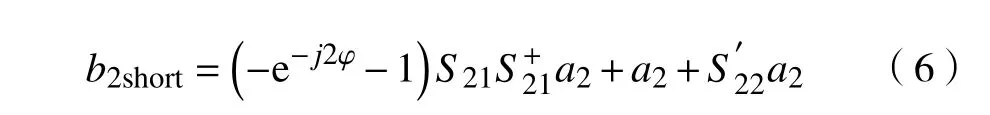
当天线在波导端口匹配时，有a1=0，代入式（4）中，可得

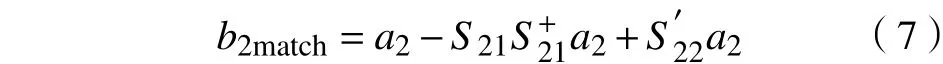
由天线产生的散射场f定义为当天线存在时的反射场与天线不存在时的反射场之差，则三种负载情况下的散射场分别为：

联立式（8）、（9）和（10）可以得到

式（11）表示天线负载匹配时的散射，属于二分类法中的结构项散射. 式（12）和（13）有明确的物理意义，其中式（12）表示模式项散射的最大值，也表示带相移的伴随散射，天线负载不匹配时，失配散射为式（12）由反射系数加权；式（13）表示额外项散射. 至此，天线的三部分散射，额外散射σI，伴随散射σII，失配散射σIII可以从测量上实现分离.

2.2 天线三部分散射的测量分离实现

实验研究的对象是X波段波纹喇叭天线，选择中心频率10 GHz进行测量，选择天线E面，测量系统收发天线和被测天线极化匹配，都是HH极化. 测量方位角度范围为-90～90°，间隔0.5°. 波纹喇叭天线的基本测量状态有三种，分别是短路、开路和匹配. 波纹喇叭天线的原始状态见图1，矩圆波导转换后接了一段120 mm直波导，短路状态采用在直波导末端连接短路片实现，开路状态通过在直波导末端连接四分之一波长延迟线和短路片实现，匹配状态采用在直波导末端连接匹配负载实现，由于匹配负载尺寸较长，实验中为了减少外形的影响，在负载外包裹了吸波材料. 波纹喇叭天线的三种负载状态如图2（a），天线短路、开路和匹配三种状态的测量结果见图2（b）.

从测量结果看，在小角度范围内，天线短路、开路和匹配三种状态的测量结果差别较大，此时失配散射和伴随散射应该是主要部分. 三条曲线中，短路反射最高，开路反射最低，匹配反射介于两者之间. 这个结果说明匹配状态的散射并非最低，匹配时的散射包括伴随散射和额外散射，有降低的可能. 另外，开路时的散射在方位角0°位置与匹配散射相当，说明未发生伴随散射被负载失配散射完全抵消的现象. 根据前面的推导，应该是因为串联了直波导，造成负载失配散射与伴随散射并非刚好反相，从而无法完全抵消.

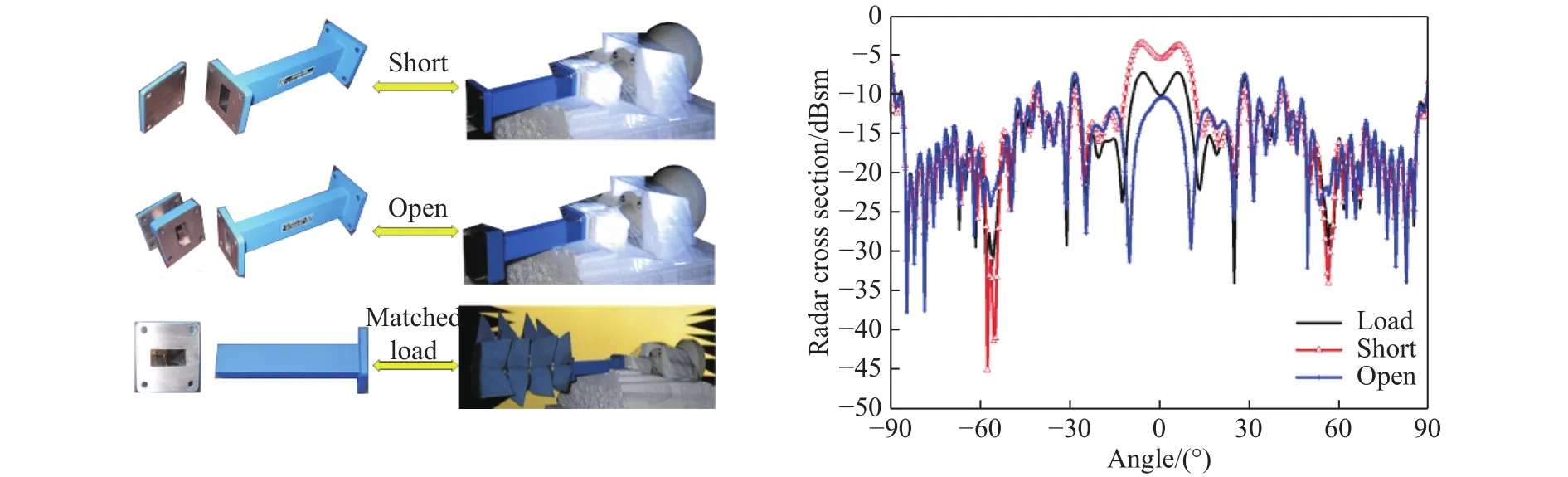
图 2 波纹喇叭天线的三种负载状态（a）及天线短路、开路和匹配三种状态的测量结果（b）Fig.2 Three load states of corrugated horn antenna (a) and measurement results of antenna under short-circuit, open-circuit, and matching states (b)

3 天线额外散射、伴随散射和失配散射的分离

根据式（11）～（13）可知：开路散射与短路散射矢量和的一半与匹配散射相等；开路散射与短路散射矢量差的一半等于伴随散射进行一定相移；匹配散射与伴随散射移相后可以抵消得到额外散射.

按照这个思路对测量结果进行处理，得到一些散射分量的结果（图3）.

图 3 运算得到的匹配散射、带相移的伴随散射Fig.3 Calculated matching scattering and phase-shifted associated scattering

运算得到的散射是否正确需要验证，马上可以验证的是匹配散射. 天线端接匹配负载的测量结果与运算得到的匹配散射曲线见图4和5.

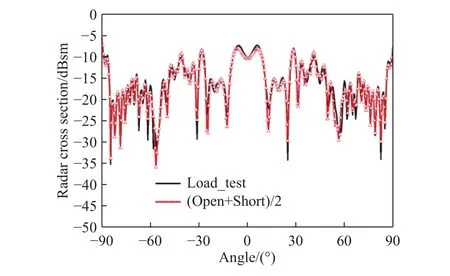
图 4 测量与运算得到的匹配散射Fig.4 Matched scattering obtained by measurement and calculation

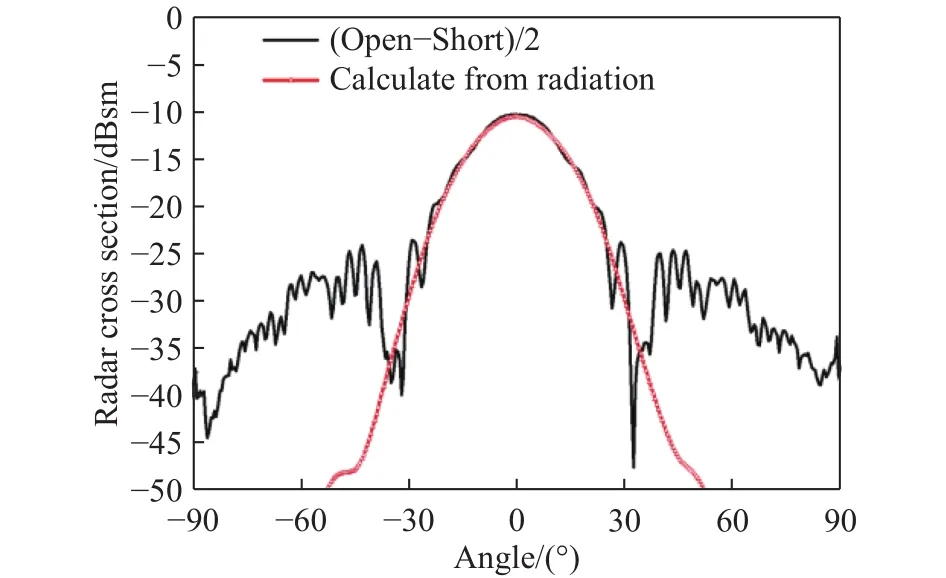
图 5 开路短路散射和方向图分别计算的伴随散射Fig.5 Associated scattering calculated by open-circuit and short-circuit scattering and pattern, respectively

从图4的结果看，匹配状态下测量得到的匹配散射与通过短路、开路运算得到的匹配散射一致性很好. 对于天线的伴随散射，根据推导，伴随散射与增益G有关，只要天线增益和工作波长确定，那么伴随散射也就随之确定. 根据前面仿真得到的波纹喇叭天线增益曲线可以计算得到天线的伴随散射，将此结果与通过短路、开路运算得到的伴随散射比较，见图5. 在±30°范围内，通过开路、短路散射计算的伴随散射和通过方向图计算的伴随散射一致性很好. 较大方位角处，由于伴随散射较低，通过测量数据进行的运算无法得到太低的数值，两者会有偏差，但此时伴随散射的量级很小，可以忽略. 从图2（b）可知，在小角度范围内，天线终端接匹配负载、开路、短路三种状态的散射差别较大. 根据分析，天线终端接不同负载时仅影响失配散射，因此可以判断，小角度时天线的伴随散射、失配散射占主要部分. 如果调整天线的终端状态，使伴随散射和失配散射相互抵消，则可能会得到较低的散射. 观察天线的匹配散射相位与运算得到的伴随散射相位，见图6，发现两者在方位角0°处有103.4°的相位差，说明运算得到的伴随散射带有相移.

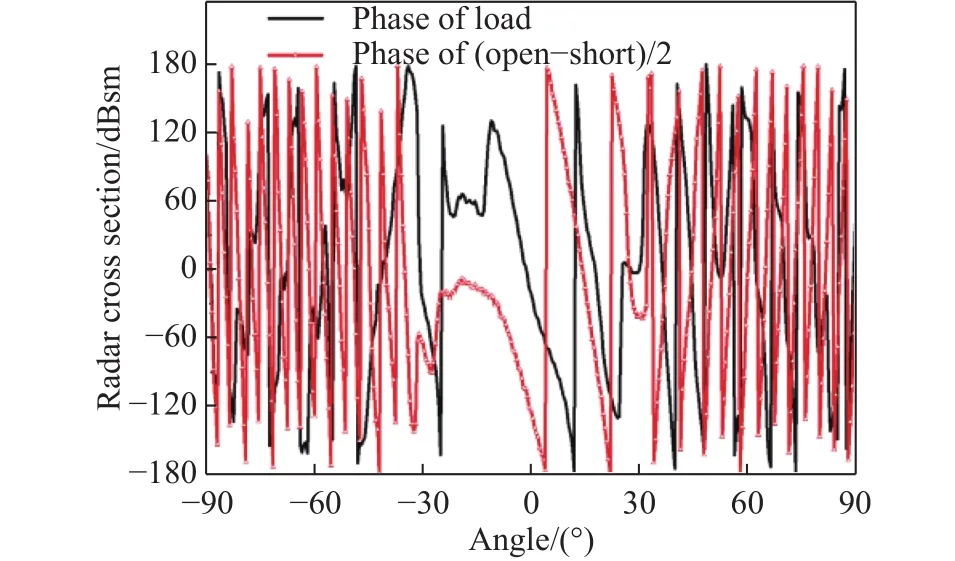
图 6 匹配散射、运算得到的带相移的伴随散射相位Fig.6 Phase of matched scattering and calculated associated scattering with phase shift

根据前面推导，串联直波导引起的作用就是使失配散射产生相移，而对失配散射强制相移也相当于模拟了串联直波导的长度. 因此，可以通过改变失配散射相移的方式，获得在实际短路点运算得到的失配散射与伴随散射的相位差. 判断的依据是匹配散射与失配散射叠加后，可以获得最小的额外散射. 如图7所示，当负载反射系数|Γ|=1时，失配散射和伴随散射幅度相等，但是由于串联了透明网络，两者相位差具有随意性，但是在失配散射矢量平面旋转一周肯定会有一个角度与伴随散射抵消，只剩下额外散射，如图8所示.

图 7 失配散射与伴随散射抵消示意Fig.7 Cancellation of mismatched scattering and associated scattering

图 8 波纹喇叭天线的额外散射Fig.8 Excess scattering of corrugated horn antenna

至此，通过运算得到了天线的三部分散射，即额外散射σI，伴随散射σII，失配散射σIII. 根据分析，天线的散射应该介于一个最大值和最小值之间，最小值基本上与额外散射σI相当，而最大值基本上与σI+2σII相当. 计算得到的最大值和最小值如图9所示.

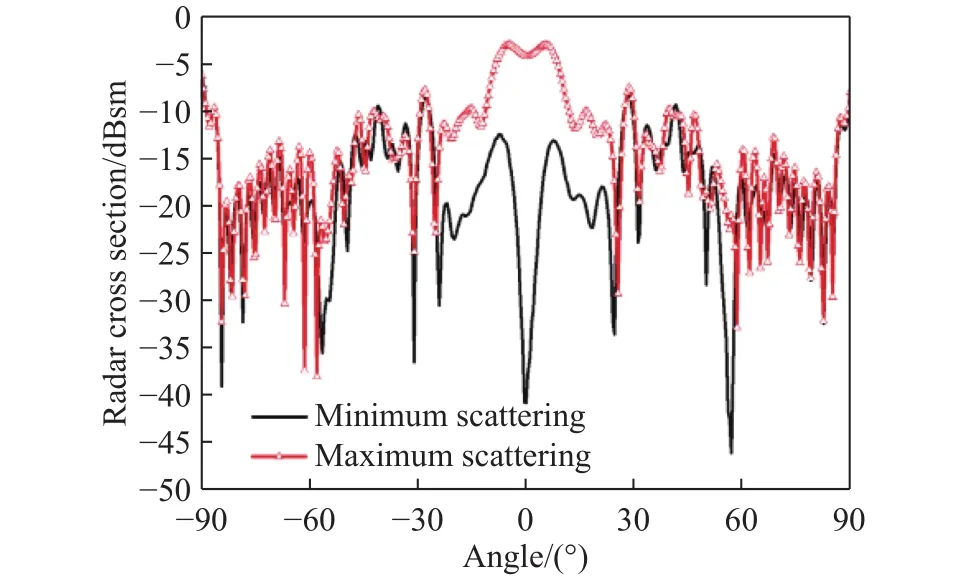
图 9 波纹喇叭天线散射的最大值和最小值Fig.9 Maximum and minimum scattering of corrugated horn antenna

实际测量得到的天线散射基本应该介于最大值和最小值之间.

4 天线最小散射实验验证

第3部分对波纹喇叭天线短路、开路和匹配的三种基本测量状态的散射进行运算，得到了波纹喇叭天线的可能散射区间. 那么，实际中是否存在运算得到的散射最大值和最小值呢？结果尚有待于实验验证. 按照第2部分推导，天线短路状态可以实现最小散射. 只要有一个可变长度大于半波长的可调短路器，就可以实现波纹喇叭天线的最小散射，这给波纹喇叭天线散射区间的验证带来很大方便. 实际使用的波导滑动短路器可调长度30 mm，大于10 GHz时的导内半波长，见图10.

图 10 验证天线散射区间用的滑动短路器Fig.10 Sliding shorter for verifying the scattering range of the antenna

而根据图6测量得到的相位关系，可知φ=-38.3°. 根据式（8），当e−j2φ=1时可获得额外散射，而当φ=k×180,k=0,±1,±2,···时，有e−j2φ=1.波导口延长会使φ增加，当φ增加38.3°后，φ变为0°，此时如果使天线开路，应该可以得到波纹喇叭天线的额外散射. 根据前面的推导，波导口再延长四分之一波长，则天线短路时也可以获得额外散射. 这相当于滑动短路器移动128.3°. 频率为10 GHz时，BJ100标准矩形波导的导内波长为40 mm，相移38.3°相当于移动4.26 mm，相移128.3°相当于移动14.26 mm. 滑动短路器移动4.26 mm相当于天线短路，此时应该获得最大散射，滑动短路器移动14.26 mm相当于天线开路，此时应该获得波纹喇叭天线较小的额外散射.

按此结果，在滑动短路器刻度14 mm处进行测量，结果如图11（a）所示.

从图11（a）可以看出，滑动短路器移动14 mm的散射与计算得到的额外散射有一定差距，不过已经比天线连接开路器的散射要低. 估计获得额外散射的位置就在14 mm附近，通过调整滑动距离应该可以获得与推算结果相当的额外散射. 经过多次调整，在滑动短路器移动13 mm处获得了与推算结果相当的额外散射，此时失配散射与伴随散射反相抵消，天线总散射较小. 与之相对应，在滑动短路器移动3 mm处获得了较大的散射，此时失配散射与伴随散射同相叠加，天线总散射较大，如图11（b）所示. 测量中出现额外散射的位置与推算的位置有一定偏差，出现偏差的原因应该是推算位置时用到了天线接匹配负载状态的散射相位，而天线匹配状态的散射除了伴随散射外还有额外散射. 受额外散射影响，天线接匹配负载状态的散射相位与天线伴随散射的相位不一致，所以用匹配状态的相位推算滑动短路器位置时会有偏差. 偏差的大小应该与额外散射的大小有关，对于波纹喇叭天线，方位角零度附近额外散射较小，推算出来的偏差有1.26 mm. 这样，就从实验中获得了理论推算的天线散射最大值、最小值. 从而也验证了天线散射可以分为额外散射、伴随散射、失配散射的结论.

图 11 滑动短路器的散射. （a）14 mm处；（b）3 mm和13 mm处Fig.11 Scattering while using sliding shorter: (a) at 14 mm; (b) at 3 and 13 mm

5 结论

针对大规模阵列天线的互耦问题，本论文专注于研究天线单元本身的散射特性. 推导了负载短路状态下最小散射天线的散射矩阵，比Kahn提出的负载开路状态下最小散射天线更适于进行仿真和实验研究. 对波纹喇叭天线连接短路器、开路器和匹配负载三种不同状态进行了散射测量，结合理论推导结果，对天线额外散射、伴随散射、失配散射进行了分离. 分离之后的伴随散射和由天线方向图计算得到的伴随散射一致性很好，验证了理论推导的正确性. 用分离之后的散射分量推算了波纹喇叭天线的散射最大值和最小值，用滑动短路器作为可变负载进行测量，实测结果验证了理论推算的正确性. 该结果也说明，在进行大规模阵列的单元天线设计时，除了考虑单元天线的辐射特性之外，也要考虑天线的散射特性，以降低天线的互耦效应.