协同式多目标自适应巡航控制

章军辉，李 庆，陈大鹏✉

1) 中国科学院微电子研究所，北京 100029 2) 江苏物联网研究发展中心，无锡 214135 3) 无锡物联网创新中心有限公司，无锡 214135

早期自适应巡航（Adaptive cruise control, ACC）系统设计主要是为了满足驾乘舒适性与车辆安全性需求，而随着智能交通系统（Intelligent transportation system，ITS）的快速发展，利用自动化高速公路（Automated highway system，AHS）来加强高速公路安全建设，缓解交通拥堵以及改善道路通行能力已引起研究人员与汽车制造商的高度重视[1−4].

目前，量产ACC普遍采用固定时距（Constant time headway, CTH）策略[1, 5]，该策略下对车间时距的选取极具挑战性. 当时距预设过小时，会造成驾乘人员心理紧张不适，亦增加了追尾碰撞的潜在可能性，而当时距预设过大时，不仅会降低道路通行能力与吞吐量，还可能会诱发邻道车辆并线、强插等不文明事件.

单车ACC系统设计时，对车间时距的选取，主要基于前后两车之间的跟驰安全性考虑[6−7]. 国外如英国与法国给出的时距参考值为2.0 s，德国的为1.8 s[8]，这些时距预设值相对偏保守，会造成一定的道路交通带宽浪费. 此外，不同驾驶群体对车间时距预设的偏好不一，存在用户体验友好性不足的问题，从而离线参数标定、在线学习更新亦成为一种设计趋势[9−10].

多车协同自适应巡航控制（Cooperative adaptive cruise control, CACC）作为AHS的典型应用，已成为研究前沿与热点. 文献[1]通过搭载毫米波雷达来组建Radar_ACC车队，采用滑模控制（Sliding mode control, SMC）方法，着重分析了车间时距的选取对车队稳定性的影响. 文献[2]分别搭建了基于毫米波雷达的Radar_ACC车队，以及基于车车（Vehicle-to-vehicle,V2V）通信的V2V_ACC车队，采用H∞控制方法，并给出Radar_ACC车队稳定所要求的最小车间时距要大于V2V_ACC车队的最小车间时距这一结论，从而也进一步表明V2V通信技术对道路通行能力的提升具有潜在优势. 文献[3]提出了一种最小安全车距的ACC车队控制策略，以避免由于前车加速度的不确定性而可能会导致的追尾事件.

关于多车协同控制系统稳定性问题，除了上述车间时距外，车队规模、瞬态工况、控制器设计（如巡航过程中控制目标权重分配、控制策略等）、车辆动力学特性、非常态环境等因素皆有可能会影响到车队稳定性以及车队整体品质（如车队响应时间、车距误差束波动幅度、工况适应能力等），因而，本文将对此进一步展开. 首先，考虑到V2V通信技术的先进性与优越性[11]，本文搭建了基于V2V通信的CACC车队模型，分别对同质与异质车队稳定性进行了量化分析. 接着，基于模型预测控制（Model predictive control，MPC）理论，综合协调驾驶员期望响应（如动态追踪性能、燃油经济性能、驾乘舒适性能等）、跟驰安全性、车队稳定性、车队整体品质等控制目标. 最后，设计了稳态舒缓工况、瞬态急加速工况以及瞬态急减速工况，对巡航过程中的车队稳定性、车队整体品质等车队响应进行了分析与探讨.

1 CACC车队稳定性

V2V车车通信技术能够实现一定范围内车辆之间速度、位置、油门、制动等信息实时可靠传递与共享，从而可将搭载V2V通信模块的CACC车队视为一个互联系统. 图1为CACC车队互联系统示意图，其中编号为0的视为领车.

图 1 搭载V2V模块的CACC车队示意图Fig.1 Sketch of CACC platoon equipped with V2V real-time communication technology

根据李雅普诺夫稳定性定理，作如下定义.

定义1车队互联系统稳定性

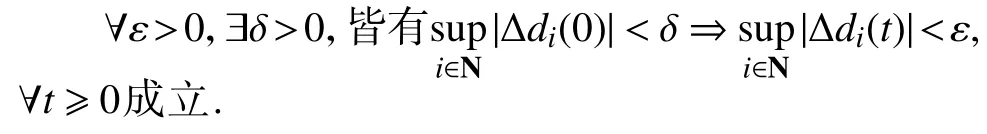
定义2车队互联系统渐近稳定性

式中，∆di=di−di,des为 车队中第i（i≥1）辆车与第i−1辆车之间的车距误差，di与di,des分别为第i辆车与第i−1辆车之间的实际车距与期望车距，∆vi(t)=vi−1(t)−vi(t)为第i辆车与第i−1辆车之间的相对速度，t为时间.

车队互联系统稳定则要求车队头部车距误差不会朝着车队尾部放大传播[1−2]. 车距误差是否衰减传播可由传递函数的无穷范数来判定，若车距误差传递函数的L∞范数不大于1，则车队互联系统是稳定的，即

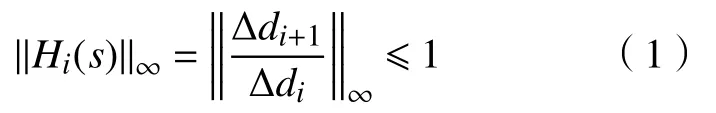
式中，Hi(s)为车队互联系统车距误差传递函数，s表示s域.

1.1 同质车队

假设每辆车所采用的控制律、CTH策略、车辆动力学特性等皆完全一致，即同质车队.

研究[1]表明，同质车队稳定的条件为

式中，τh为同质车队中邻车间的时距，TL为车辆执行系时滞，TD为通信时延.

当忽略时延TD时，选取大于2TL的时距τh，可维持车队稳定性；当忽略时滞TL时，选取大于2TD的时距τh，可维持车队稳定性.

1.2 异质车队

同质车队适宜于诸如物流车队等特殊作业场景，其稳定性分析具有一定的工程参考价值. 而实际应用中，由于汽车制造商、零部件供应商等之间没有统一的设计标准，ACC预设时距、控制律、车辆执行系等一般都存在着差异性.

研究[1]表明，异质车队稳定的条件为

综上，同质车队稳定时，车距误差呈衰减传播趋势；而对于异质车队，一则要求速度追踪能力，二则要求车距误差收敛于平衡点邻域范围内的保持能力.

当车队规模较小时，可适度放宽对上述条件的约束，而当突发瞬态工况时，又会进一步收紧约束，此外，多目标权重分配、路面附着能力等因素也会影响到车队稳定性，故需综合考虑这些实际因素来探讨车队稳定性.

2 多目标协同控制算法

如图2所示，CACC系统采用自顶向下式设计，其基本思路是：基于既定的纵向期望车距策略，决策控制层对协同跟随过程中多个且彼此相互冲突的子目标进行综合协调控制，寻求满足各个性能指标最优折衷时的自车纵向期望加速度ai,des；执行层通过控制油门/制动踏板使得自车的实际加速度ai收敛于决策层输出的期望加速度ai,des. 其中，i(i≥1)代表协同跟随过程中的第i辆车的编号，θi、Pi,brk分别为节气门开度与制动压力.

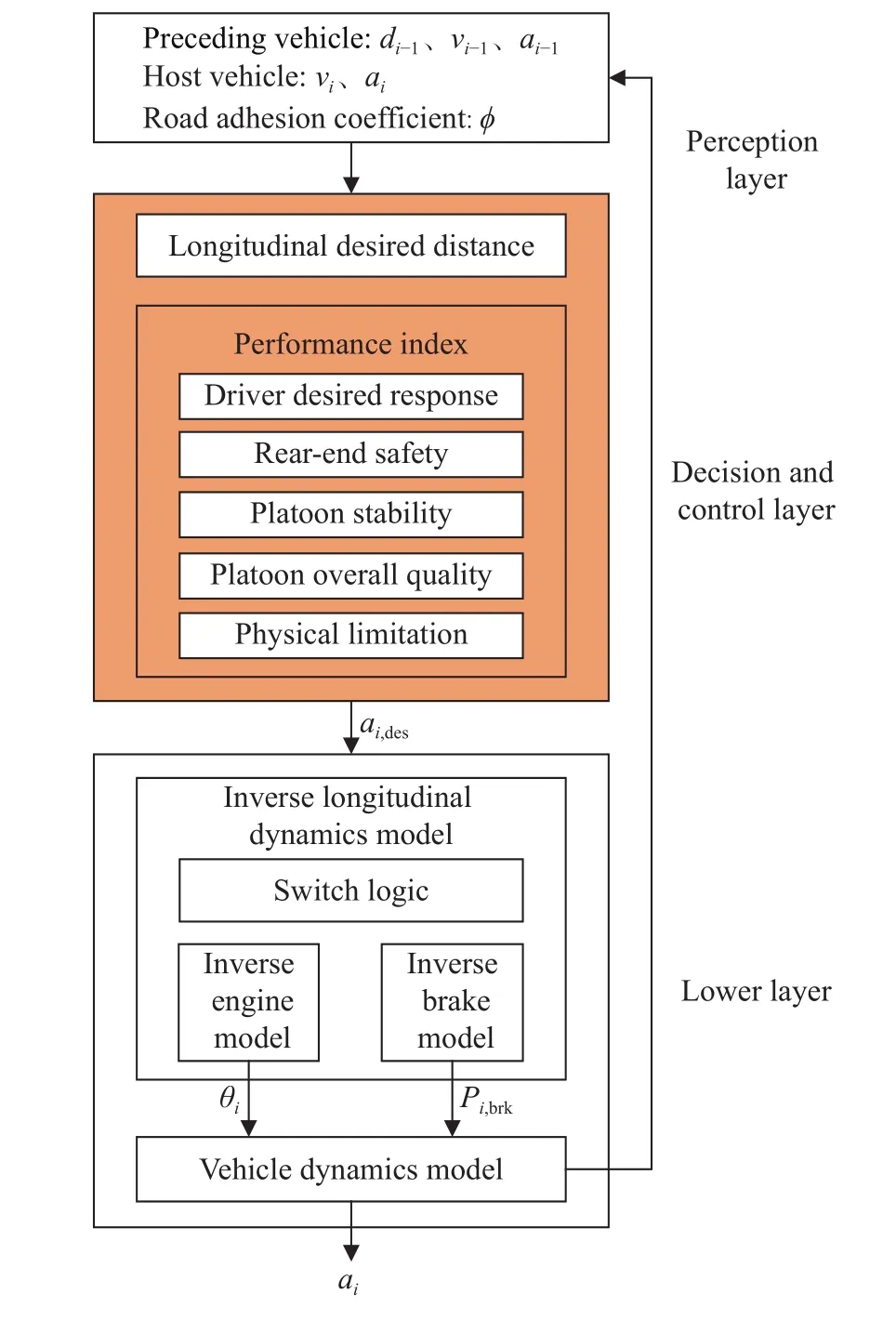
图 2 CACC分层设计Fig.2 Hierarchical architecture of CACC

2.1 数学建模

2.1.1 纵向运动学模型

如图3所示，为方便分析，将车队中第i（i≥1）辆车视为自车，第i−1辆车视为前车，当i=1时，前车即为领车，亦不失一般性.

假设期望车距采用CTH策略，车辆执行系满足一阶惯性环节. 根据纵向跟车运动学特性，令x(k)=[∆di(k),∆vi(k),ai(k)]T，以x(k)为状态向量，ui(k)为控制输入，前车加速度ai−1(k)为系统扰动，y(k)为系统输出，采用差分近似法建立离散状态空间方程

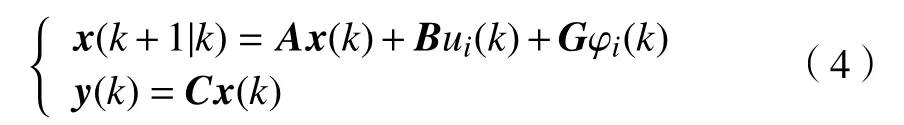
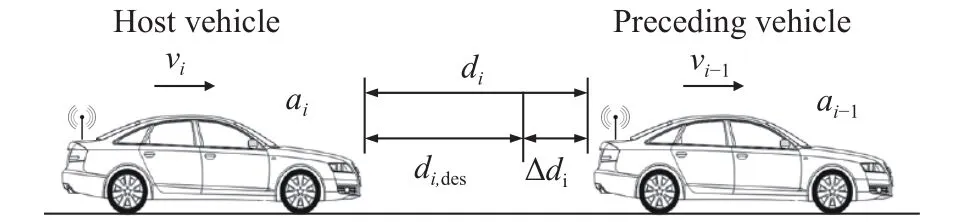
图 3 CACC纵向运动学示意图Fig.3 Longitudinal inter-vehicle dynamics of CACC

式中，ui(k)=ai,des(k)，φi(k)=ai−1(k)，k为离散时间，各系数矩阵满足

其中，I为单位矩阵，Ki,L为增益，Ti,L为时间常数.

2.1.2 鲁棒设计

考虑到工程实际路面附着情况，对CTH策略中的零速度车距d0进一步修正，以补偿路面湿滑所导致较长的安全制动距离.

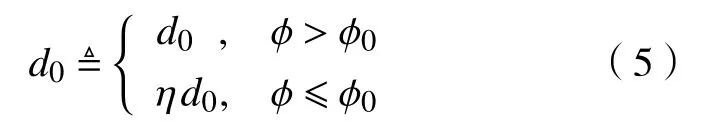
式中，ϕ为路面附着系数，ϕ0为参考值，η为修正系数.

此外，为提高式（4）对真实系统的辨识表达能力，基于闭环反馈校正思想，引入误差修正项e(k)，以期提高模型预测精度以及抗干扰能力[12].

所以，将式（4）改写成

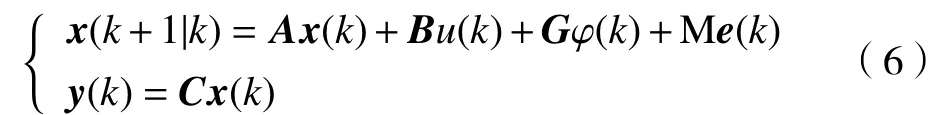
式中，M=diag(m1,m2,m3)为校正矩阵，e(k)=x(k)−x(k|k−1)为误差修正项，其中，x(k)为k时刻系统实际状态，x(k|k−1)表示k−1时刻对k时刻状态的预测.

2.1.3p步预测模型

假设当前时刻为k，p步预测时域为[k，k+p−1]，由离散状态空间方程（6），逐步迭代并整理得

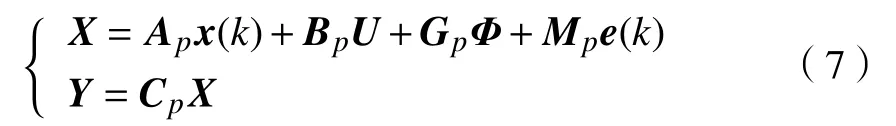
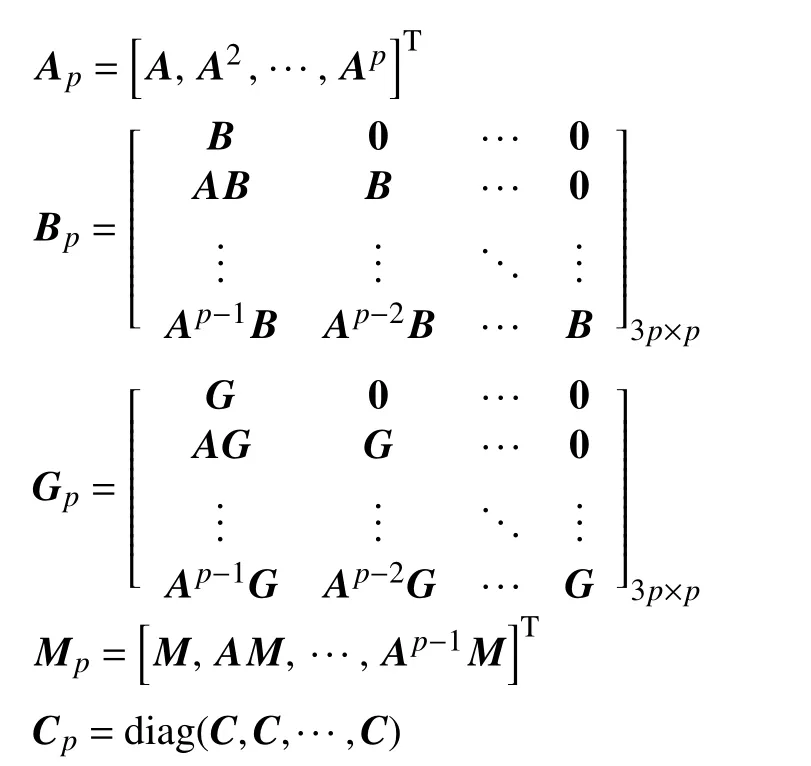
2.2 控制目标分析

2.2.1 驾驶员期望响应

采用二次型形式来间接表征动态追踪性能、燃油经济性能、驾乘舒适性能等性能指标，建立起相应的性能泛函，作为待优化的子目标[13].

（1）动态追踪性.

动态追踪性间接评价方法[14]：车距误差∆di与相对车速∆vi皆收敛于期望邻域U(0,σ)内的能力，其中，σ为邻域半径. 其二次型表示为式中，w∆di、w∆vi分别为∆di与∆vi的权重系数.

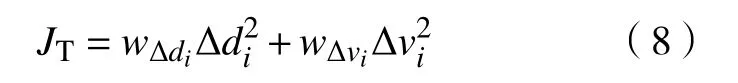
（2）燃油经济性.

燃油经济性间接评价方法[15]：利用期望加速度ai,des与冲击度ji的二次型来间接评估燃油经济性，即

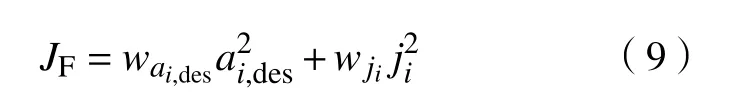
（3）驾乘舒适性.

良好驾乘体验间接评价方法[12]：跟驰过程中车距误差∆di的收敛性；ai,des与ji于可容许控制集内的保持能力；驾驶员主动干预后的响应能力.

由于部分性能指标已在式(8)、式(9)中有体现，故其二次型简化为

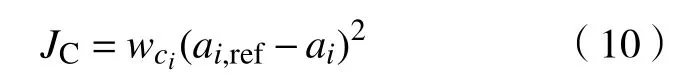
式中，wci为相应权重系数，ai,ref=kv∆vi+kd∆di为驾驶员参考加速度[16]kv、kd分别为相应权重系数.

2.2.2 跟驰安全性

跟驰安全性约束条件为

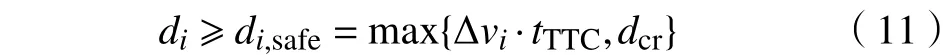
式中，tTTC为碰撞时间，表示制动安全性[13]，di为实际车距，di,safe为安全跟车车距，dcr为安全车距临界值.

2.2.3 车队稳定性

（1）车间时距.

由上文分析结论知，对于CTH策略而言，车间时距约束如下

式中，τcr为车队临界稳定时所对应的车间时距.

（2）车队规模.

当车队规模为2且满足式（11）时，车队是稳定的. 当车队规模逐渐扩大时，车队保持稳定的能力会下降，故而约束如下

式中，Ncr为车队临界稳定时的车队规模.

这里不考虑因邻道车辆并线而引入的外部扰动.

（3）其他因素.

车辆跟驰过程中过于追求追踪性等性能指标，抑或瞬态工况皆有可能使车队失稳[17]. 亦即，不同跟随工况下，需合理分配控制目标权重，谨慎松弛约束空间的边界约束.

2.2.4 车队整体品质

CACC巡航过程中，通过车队响应时间、车距误差束波动幅度、工况适应能力等指标来间接评估车队整体品质.

2.3 多目标决策控制算法

2.3.1 代价函数及线性约束条件

为满足驾驶员跟驰过程中的期望响应，基于MPC框架对多目标进行协调控制，建立预测时域为[k，k+p−1]的代价函数

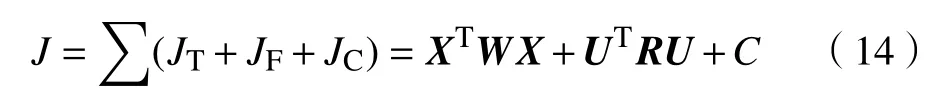
式中，C为常数项，

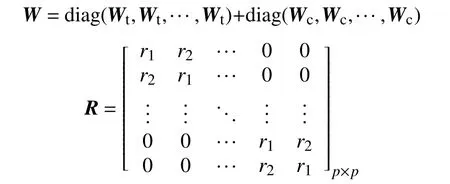
其中，

考虑到车辆自身物理限制等因素，需要对控制器工作域进行边界约束[12]，从而建立过程状态与系统I/O约束条件如下.

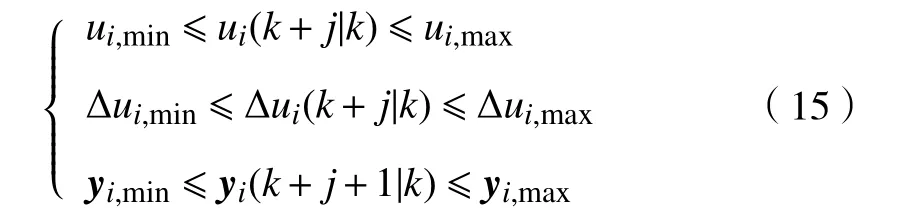
式中，j∈[0,p−1]，ui,min、∆ui,min分别为可容许控制与可容许增量控制下界，分别为可容许控制与可容许增量控制上界，为系统输出下界，为系统输出上界.

2.3.2 松弛向量约束管理

（a）用户注册：在权威数据源系统（例如人力资源管理系统）中对用户进行注册，确定用户要注册的部门、岗位分配等信息，并在权威数据系统中建立用户账户。

瞬态工况下，硬约束条件易致滚动优化过程中无可行解问题，故引入松弛向量对硬约束条件进行松弛化，以扩展求解可行域[12−13].

考虑到跟驰安全性与车队稳定性的硬性约束，仅对式（15）进行松弛化处理，即

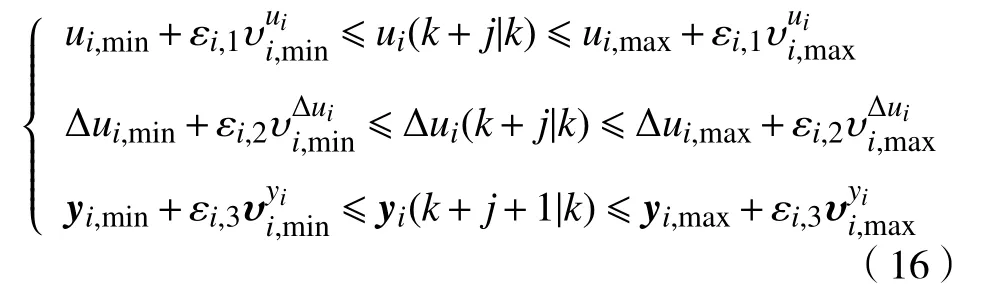
2.3.3 控制算法最终演变

为获得较好的控制品质，采用增量式控制策略. 定义当前k时刻与k−1时刻的控制输入之差为控制增量，即

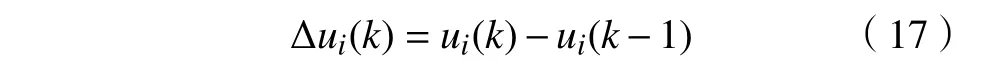
则在[k，k+p−1]预测时域内，满足

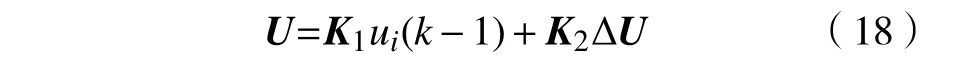
此外，求解过程中，若松弛因子自动调节过大，可能会使控制器工作域背离可容许范围，从而使得边界约束作用失效. 换句话说，此时约束最优化问题将退化成无约束最优化问题了，其实际应用场景有限.

为抑制松弛因子对约束边界的无限松弛能力，采用正则化方法，于代价函数中引入L2正则化项，使得闭环系统在约束最优化问题寻优可行性与约束边界松弛程度之间寻求平衡[7].

所以，将式（14）改写成

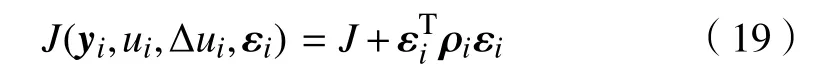
式中，εi=[εi,1,εi,2,εi,3]T为向量松弛因子，ρi=diag(ρi,1,ρi,2,ρi,3)为惩罚系数矩阵，用以惩罚松弛因子扩展约束边界的松弛能力[7].

再将式（7）、式（18）代入式（19）中，化简整理并忽略常数项得

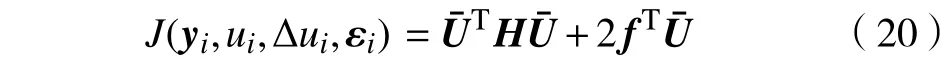
式中，

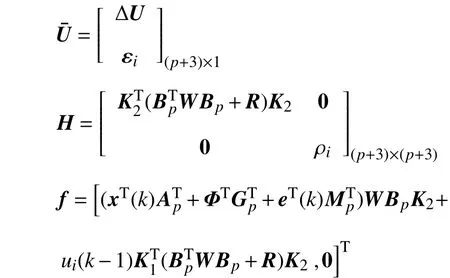
从而，在MPC模型预测控制框架下，综合协调驾驶员期望响应、跟驰安全性、车队稳定性等多个控制目标的CACC设计问题最终转化成带线性矩阵不等式约束的凸二次规划问题，即

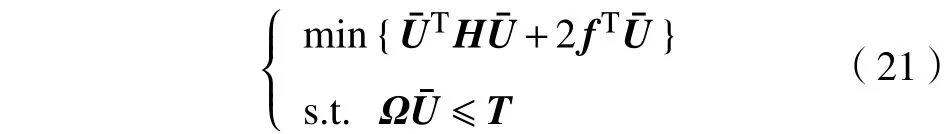
式中，

在p步有限预测时域滚动优化求解过程中，当ui,∆ui,yi未超出工作域约束边界时，松弛因子取值为0；而当其超出工作域约束边界时，相应松弛因子会自动正向增大以扩展控制器工作域，使得带约束的凸二次规划问题具有可行解.

在当前k采样周期内，通过式（21）进行优化求解，得到一串预测序列

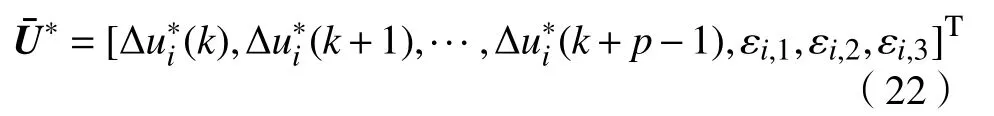
下一采样时刻，预测时域向前移动一步，并重复上述过程，从而实现CACC滚动在线控制.

3 仿真验证

本文利用Matlab/Simulink搭建了多目标CACC期望车距控制模型、逆纵向动力学模型、车辆动力学模型，稳态舒缓工况下控制算法仿真参数见表1，车辆动力学参数详见文献[10].

约定车队规模为11，领车编号为0，跟随车辆编号依次为1～10. 同质车队与异质车队的仿真参数分别见表2与表3，其中，组号表示仿真对比组号，编号即为车辆编号.

典型仿真工况如下.

（1）稳态舒缓工况.

领车初始速度为20 m·s−1，在t=10 s至t=130 s时间段内，领车保持加速度为±0.3 m·s−2的舒缓循环工况，之后保持速度为20 m·s−1的匀速状态.

表 1 控制算法仿真参数Table 1 Parameters of the CACC platoon

表 2 同质车队仿真参数Table 2 Parameters of the homogeneous platoon

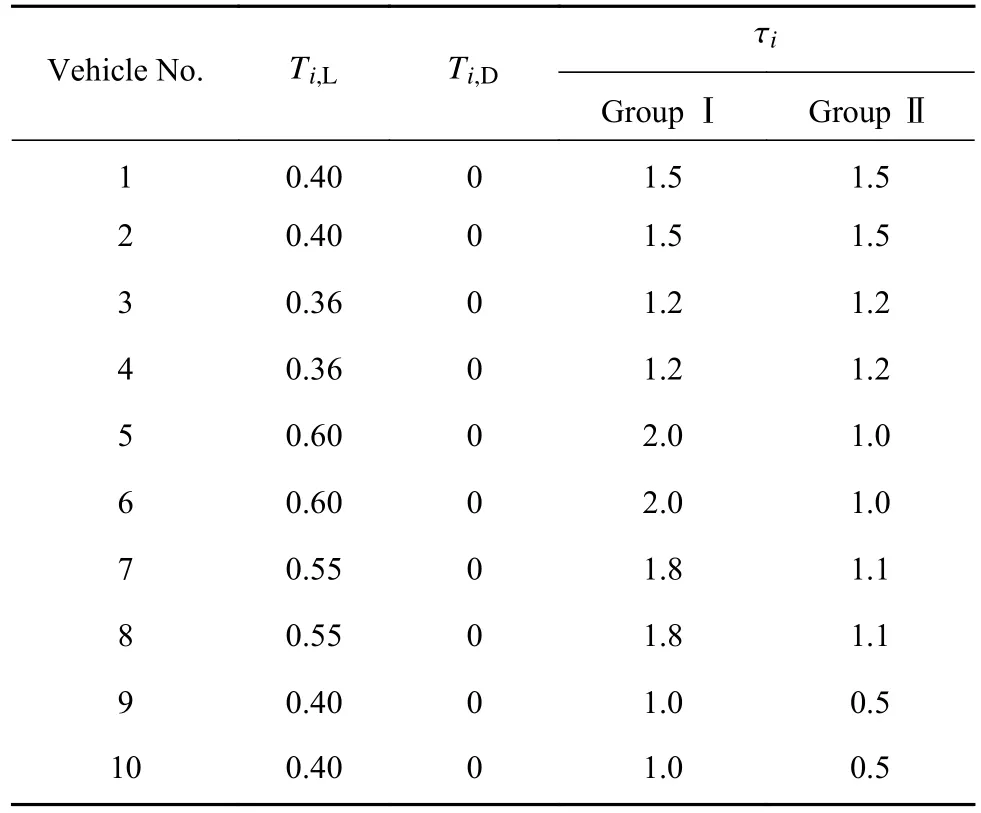
表 3 异质车队仿真参数Table 3 Parameters of the heterogeneous platoon

（2）瞬态急加速工况.

领车初始速度为20 m·s−1，于t=10 s时以1 m·s−2的加速度急加速至30 m·s−1.

（3）瞬态急减速工况

领车初始速度为20 m·s−1，于t=10 s时以−2 m·s−2的减速度急减速至10 m·s−1.

3.1 同质车队数字仿真

3.1.1 稳态舒缓工况

图4表示在稳态舒缓工况下选取不同时距τi时∆di的传播情况. 随着时距τi取值减小，车队总长逐渐变短，有益于改善道路通行能力；而另一方面，随着时距τi取值减小，误差束波动幅度逐步变大，即∆di对时距τi的敏感度渐增.

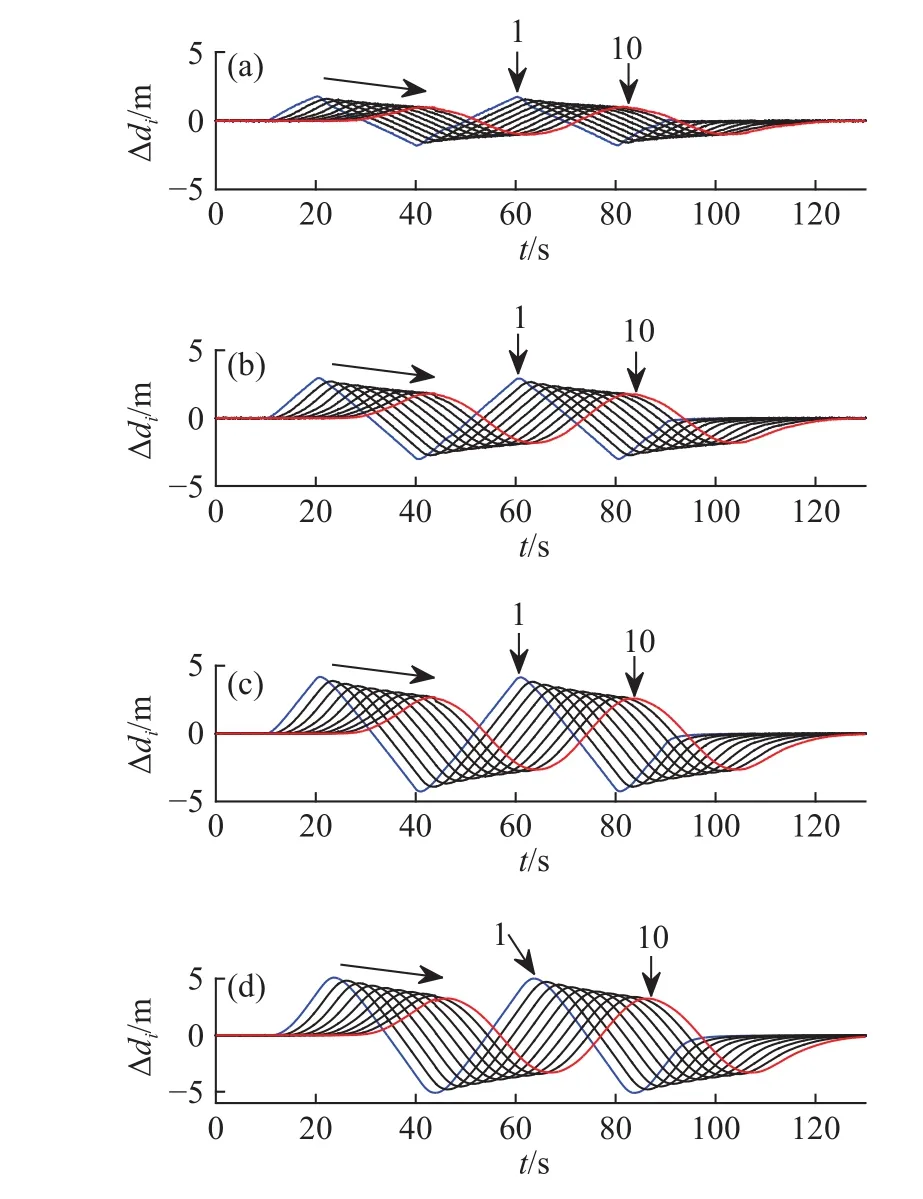
图 4 时距τi对同质车队响应的影响. （a）τi=2.0 s；（b）τi=1.5 s；（c）τi=1.0 s；（d）τi=0.5 sFig.4 Homogeneous platoon response with time gap τi: (a) τi=2.0 s; (b)τi=1.5 s; (c) τi=1.0 s; (d) τi=0.5 s

图5表示在时距τi=1.5 s的条件下，选取不同权重w∆di时∆di的传播情况. 比较易发现，随着目标权重w∆di增大，∆di传播过程中发生发散现象，表明车队行驶过程中过于追求追踪性能会影响车队稳定性.

图6亦表示在同样条件下，选取不同权重wji时∆di的传播情况. 比较易发现，随着权重wji取值增大，误差束波动幅度渐增，车队响应时间渐长，表明随着舒适性/经济性要求的提高，会带来误差束波动幅度增加、车队响应时间延长等额外开销.

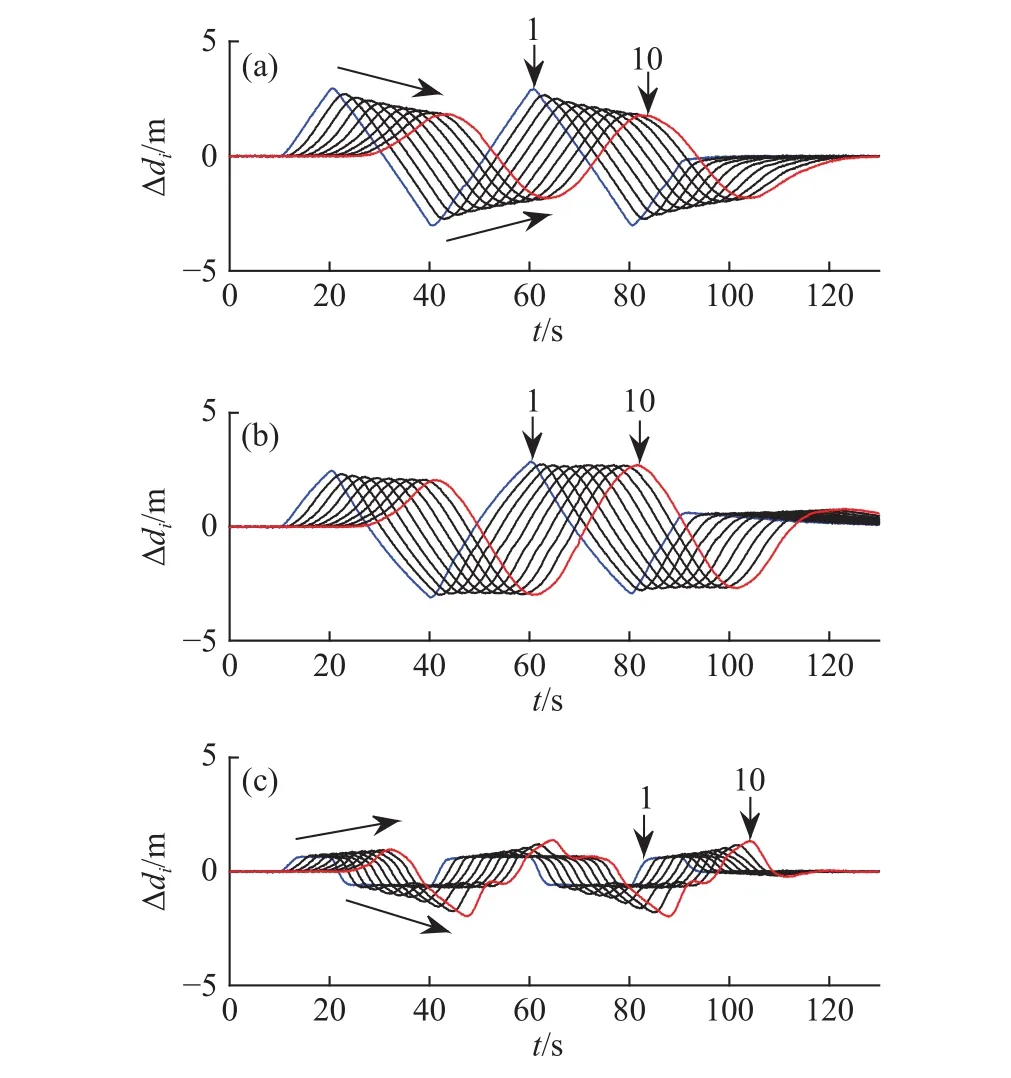
图 5 目标权重w∆di 对同质车队响应的影响. （a）w∆di=0.01；（b）w∆di=0.1；（c）w∆di=1.0Fig.5 Homogeneous platoon response with w∆di : (a) w∆di=0.01; (b)w∆di =0.1; (c) w∆di =1.0

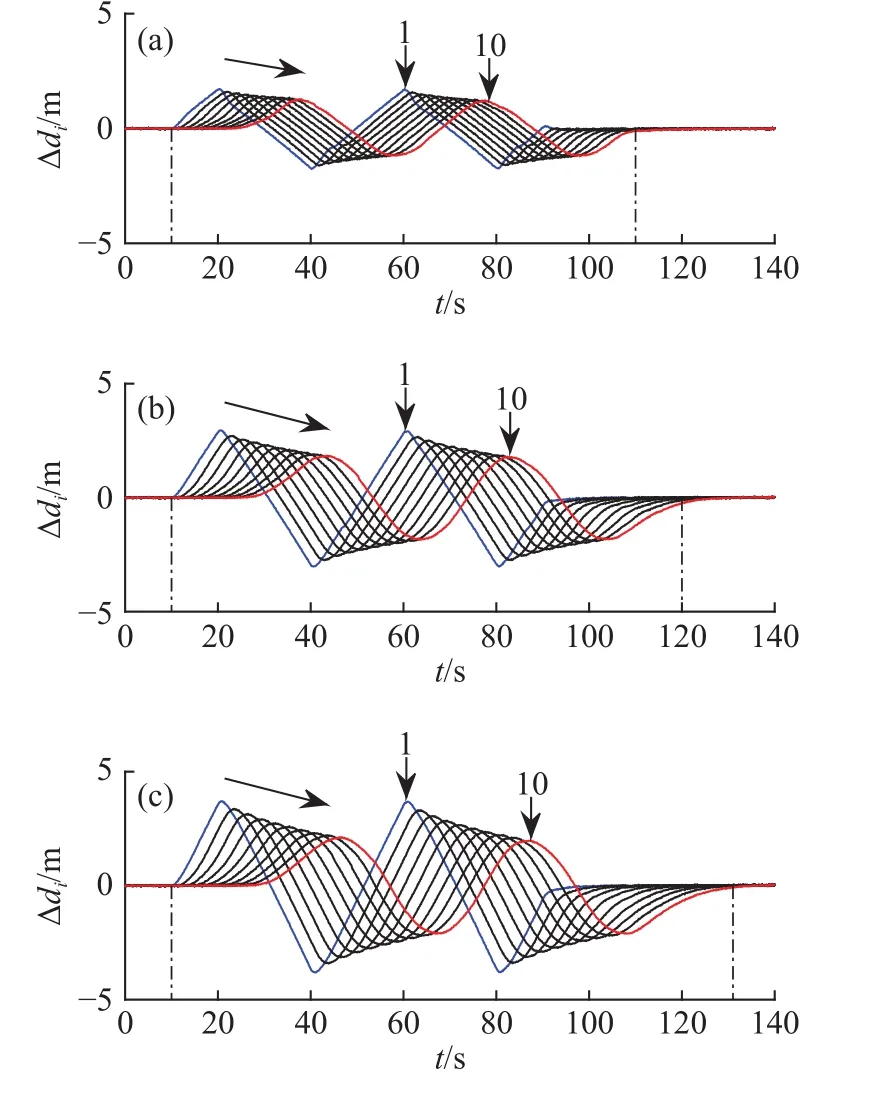
图 6 目标权重wji 对同质车队响应的影响. （a）wji=0.0006；（b）wji=0.001；（c）wji=0.0012Fig.6 Homogeneous platoon response with wji : (a) wji=0.0006; (b)wji=0.001; (c) wji=0.0012

3.1.2 瞬态急加速工况

图7表示在瞬态急加速工况下选取不同时距τi时∆di的传播情况. 如图7（a）和（b）所示，时距τi选取2.0 和1.5 s时，车队皆能保持稳定，且车距误差束波动幅度较小；而时距τi选取1.5 s时，对于CTH车距策略来说，期望车距相对较短，即车队总长相对较短，从而道路通行能力相对较好. 图7（c）中，时距τi选取1.0 s时，∆di约束能力略差. 图7（d）中，时距τi选取0.5 s时，邻车间初始车距仅有15 m，滚动求解过程中∆di边界松弛过大，追踪性能急剧下降，后车为了使∆di收敛，以超过前车车速进行追踪，使得车速被放大传播（见图8），且从第7辆车开始，边界约束条件已严重背离，从而导致车队失稳. 另一方面，时距τi选取0.5 s时，若控制好车队规模，亦有望维持车队稳定.

图 7 时距τi 对同质车队响应的影响. （a）τi=2.0 s；（b）τi=1.5 s；（c）τi=1.0 s；（d）τi=0.5 sFig.7 Homogeneous platoon response with time gap τi : (a) τi=2.0 s; (b)τi=1.5 s; (c) τi=1.0 s; (d) τi=0.5 s

图 8 时距τi=0.5 s时同质车队速度传播情况Fig.8 Propagation velocities of the homogeneous platoon when τi=0.5 s

3.1.3 瞬态急减速工况

图9表示在瞬态急减速工况下选取不同时距τi时∆di的传播情况. 如图9（a）与9（b）所示，时距τi选取2.0和1.5 s时，车队皆能保持稳定，且车距误差束波动幅度较小. 图9（c）中，时距选取1.0 s时，∆di负向约束能力稍差. 图9（d）中，时距τi选取0.5 s时，邻车间初始车距仅有15 m，∆di负向边界松弛过大，降低了跟驰安全性，最终导致整个车队失稳.

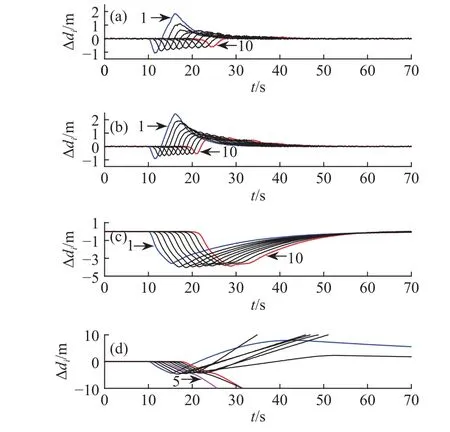
图 9 时距τi对同质车队响应的影响. （a）τi=2.0 s；（b）τi=1.5 s；（c）τi=1.0 s；（d）τi=0.5 sFig.9 Homogeneous platoon response with time gap τi : (a) τi=2.0 s; (b)τi=1.5 s; (c) τi=1.0 s; (d) τi=0.5 s

此外，仿真过程中发现，相对稳态舒缓工况而言，瞬态工况下车队稳定性对目标权重w∆di、wji较为敏感.

3.2 异质车队数字仿真

3.2.1 稳态舒缓工况

对于异质车队，跟随车辆的执行系时滞、车距策略的时距预设值不完全相同. 与组Ⅰ相比，组Ⅱ中部分时距预设值相对偏小，即邻车车距相对偏小.

图10表示在稳态工况下两组异质车队∆di的传播情况. 不难发现，与组Ⅰ相比，组Ⅱ车距误差束波动幅度稍大，是由于时距预设偏小而致，不过误差束波动幅度皆在可容许范围内，两组车队皆能维持稳定.

3.2.2 瞬态急加速工况

图11与图12表示在急加速工况下两组异质车队车距误差与车速的传播情况. 与组Ⅰ相比，组Ⅱ车距误差束波动幅度较大，车队追踪性能较差，从而导致该组车队维持稳定时的响应时间较长.

3.2.3 瞬态急减速工况

图 10 异质车队车距误差传播情况. （a）组Ⅰ；（b）组ⅡFig.10 Propagation spacing errors of the heterogeneous platoon: (a)group I; (b) group II

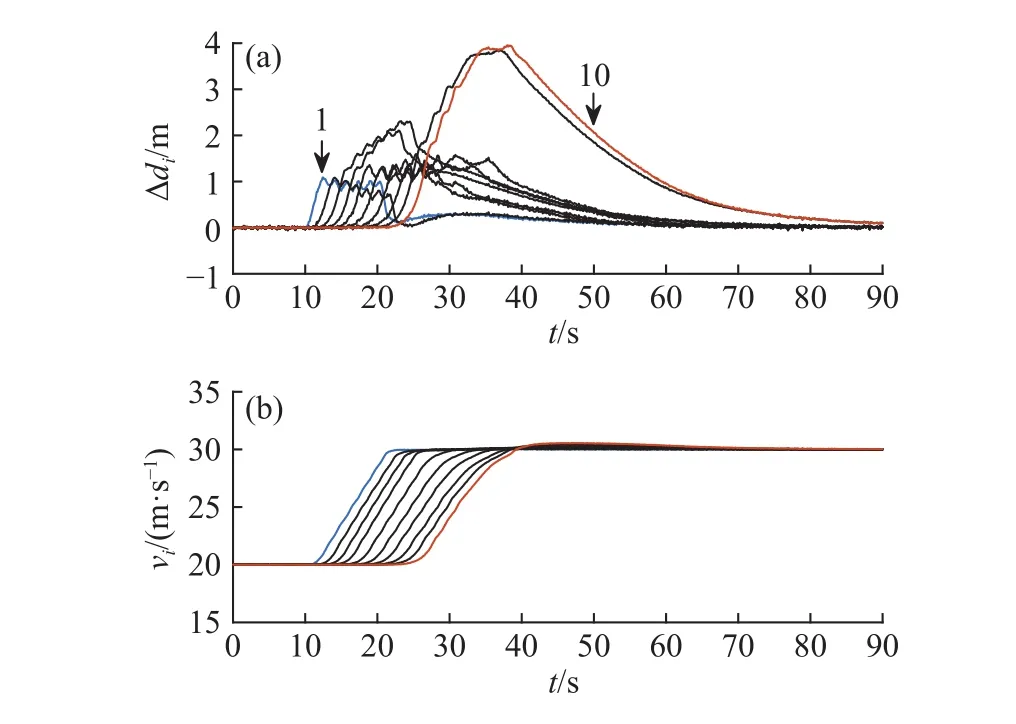
图 11 在组Ⅰ时距τi下异质车队响应. （a）车距误差；（b）车速Fig.11 Heterogeneous platoon response for group I with the preset time gap: (a) spacing error; (b) velocity

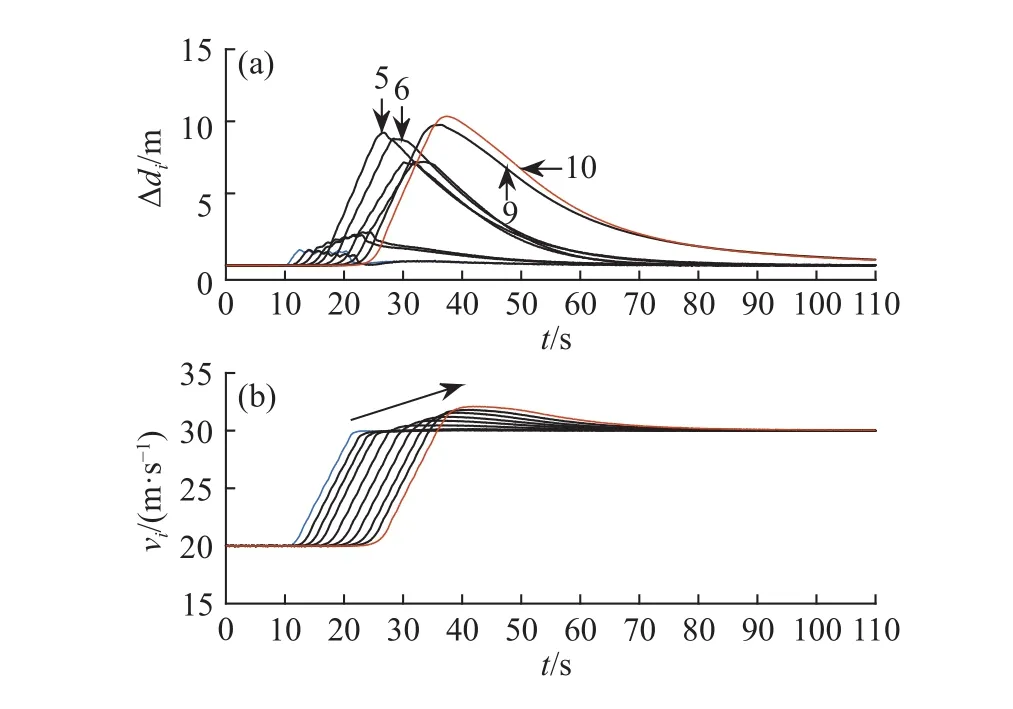
图 12 在组Ⅱ时距τi下异质车队响应. （a）车距误差；（b）车速Fig.12 Heterogeneous platoon response for group II with the preset time gap: (a) spacing error; (b) velocity

图13与图14表示在急减速工况下两组异质车队车距误差与实际车距的传播情况. 与组Ⅰ相比，组Ⅱ车距误差束负向波动幅度较大，且第9与第10辆车由于初始预设时距较小，从而在紧急制动过程中实际跟车距离较近（见图14（b）），降低了跟驰安全性.

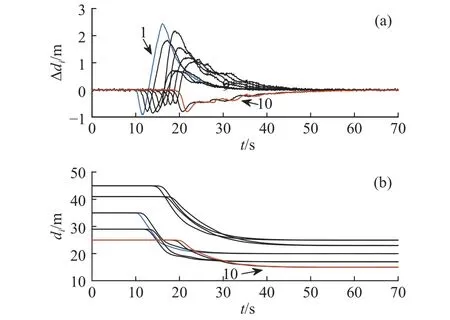
图 13 在组Ⅰ时距τi下异质车队响应. （a）车距误差；（b）实际车距Fig.13 Heterogeneous platoon response for group I with the preset time gap: (a) spacing error; (b) actual spacing

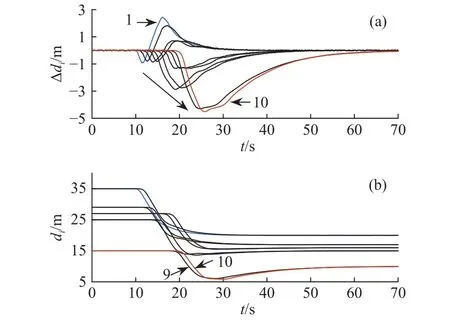
图 14 在组Ⅱ时距τi下异质车队响应. （a）车距误差；（b）实际车距Fig.14 Heterogeneous platoon response for group II with the preset time gap: (a) spacing error; (b) actual spacing

4 结论

（1）相比单车ACC而言，协同ACC的约束空间更为严苛.

（2）基于MPC框架，综合协调驾驶员期望响应、跟驰安全性、车队稳定性、车队整体品质等控制目标，采用加权二次型性能泛函以及线性矩阵不等式约束的形式，将协同ACC设计问题最终转化成带约束的在线凸二次规划问题. 同时引入松弛向量约束管理法以及抑制松弛因子作用的正则化项，使得闭环系统在约束最优化问题寻优可行性与约束边界松弛程度之间寻求平衡.

（3）仿真结果表明，车队行驶过程中过于追求追踪性等性能指标会影响到整个车队的稳定性；舒适性与经济性要求的提高，将带来车队响应时间开销以及误差束波动幅度的增加；时距取值增大使得误差束波动幅度减小，但也将导致道路通行能力下降；相对稳态舒缓工况而言，瞬态工况下车队稳定性对时距与控制目标权重较为敏感，为提高车队对瞬态工况的适应能力以及车队整体品质，建议在跟驰安全性、车队稳定性良好的前提下寻求一定的舒适性与经济性.