分布式一致性最优化的梯度算法与收敛分析

梁 舒，彭开香

北京科技大学自动化学院工业过程知识自动化教育部重点实验室，北京 100083

分布式优化是多智能体系统控制、网络通信和数学规划的赛博空间（Cyberspace）科学，在众多科学与工程中具有广阔的发展前景[1-2]. 以钢铁行业自动化为例，近年来我国钢铁生产企业普遍建立并实施了企业资源计划、生产执行系统、生产过程系统等多层次的集成自动化系统. 对于具有多层级、变工况、长流程等特点的复杂工业过程，其产品质量管控、生产计划与调度、能源综合调配等微观与宏观调控方面存在大量的优化决策问题[3]. 分布式优化理论与方法是促进两化融合战略决策和新一代工业革命的关键使能技术，其发展将增强人们对付大数据、大规模问题和复杂问题的能力，具有重要的实际应用意义并蕴藏着极大的经济效益.

分布式优化的一类抽象问题类型是一致性最优化，要求所有个体的决策变量最终实现一致性，并且一致点是一个凸优化问题的最优解. Nedic等[4−6]对该问题进行了较深入地研究，主要针对非光滑的目标函数，采用分布式次梯度的方法进行求解.其中，为了确保算法的收敛性，需要采用逐渐衰减并趋于零的步长. Shi等[7]针对无约束的光滑最优一致性，提出一种定步长并能精确收敛到最优解的分布式算法. 该算法主要的思想是对所有个体的梯度之和进行跟踪，并利用不精确梯度理论对算法的收敛性进行分析. 基于这种方法，Nedic等[8]改进了这种算法，并利用小增益的技术给出了算法的指数收敛证明. 需要指出，这类算法仅处理无约束的分布式一致性最优化问题，目前还不能推广到有约束的问题. Liu等[9]和Lei等[10]利用经典约束优化中的原始-对偶梯度方法，给出了分布式原始-对偶梯度算法. 这类算法也采用了固定的步长，能够精确收敛到最优解，而且可以处理带有约束的问题. Liang等[11]针对无约束情形下的分布式原始-对偶梯度算法，基于变分分析中的度量次正则性，给出算法指数收敛的判据，降低了对目标函数强凸性的要求. 此外，值得指出，有不少学者从连续时间微分方程的角度进行了分布式优化算法设计，如文献[12-16]. 总之，关于分布式一致性最优化问题已有不少研究，而近年来学者们更加关注分布式定步长算法，以及对它们收敛性质的分析论证.

本文考虑带有约束的分布式一致性最优化问题，给出定步长分布式原始-对偶梯度算法，并对算法的收敛性进行分析论证. 最主要的贡献在于提出一种基于李雅普诺夫函数的收敛分析范式：针对一般的定步长迭代格式，给出基于李雅普诺夫函数的收敛条件，类似于一般微分方程关于李雅普诺夫稳定的分析方法. 这种方法带来的好处在于将繁冗复杂的收敛性分析工作简化为构造李雅普诺夫函数并验证收敛条件. 在此基础上，本文将该方法应用到分布式原始-对偶梯度算法中，给出算法参数应满足的收敛条件. 与已有文献中的方法相比，如文献[9]和[10]，虽然它们从不同的角度利用算法具体结构设计构造了李雅普诺夫函数并辅助收敛分析，但本文提出的方法具有框架性和系统性，对其他类型分布式优化算法的收敛分析也具有参考价值.

下面介绍本文的记号. R 和Rn分别代表实数空间和n维 欧氏空间. 记〈x,y〉为向量x和y的内积，分别代表2-范数和无穷范数.对于N个列向量x1,···,xN，使用col(x1,···,xN)代表其堆栈而成的列向量. 用0n、1n分别表示分量全部为0和分量全部为1的列向量，用In表 示Rn×n中的单位阵. 对于矩阵A=[aij]，aij代表该矩阵在第i行第j列的元素. 符号⊗表示矩阵的Kronecker乘积.

1 预备知识

本节的主要目的是罗列后续论述所需的预备知识，包括凸集与凸函数，以及图论.

1.1 凸集与凸函数

本段介绍凸集及其投影的相关定义和性质，更详细的论述可参考专著[17]. 设Ω是n维欧氏空间Rn中的集合. 若对任意x,y∈Ω和0<τ<1，均有τx+(1−τ)y∈Ω，则称Ω为凸集. 若一个集合中任意点列的极限点仍然属于该集合，则称该集合是闭集. 定义为点z∈Rn到闭凸集合Ω的欧氏距离投影. 投影算子具有一个基本性质：〈z−PΩ(z),PΩ(z)−x〉≥0,∀z∈Rn,∀x∈Ω.

本段介绍凸函数的基本概念和性质，更多结论可参考文献[18]. 设Ω⊂Rn为凸集，f:Ω→R为一个实函数. 如果对任意x,y∈Ω和0<τ<1，均有f(τx+(1−τ)y)≤τf(x)+(1−τ)f(y)，则称f为凸函数.当f可微时，其梯度记为∇f(x). 可微凸函数具有一个基本性质：

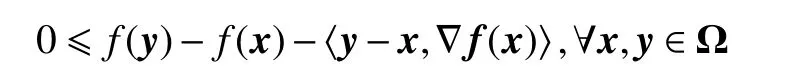
此外，若映射∇f(x)关于x是κ-Lipschitz连续的，其中κ>0为某个常数，则不论f是否是凸函数，都有下面不等式成立：

1.2 图论

网络节点之间的信息分享关系可以通过图论中的基本概念进行描述. 一个图G由 节点集合V和边集E 构成，记为G=(V,E). 对于具有N个节点的网络，通常记V={1,···,N}. 边集E⊂V×V刻画了节点之间的信息分享关系：若无序节点对(i,j)∈E，那么节点i和节点j可以相互通信. 如果对于任意i,j∈V，都可以从节点i出发通过若干条边连接到节点j，则称G为连通图. 另外，可以通过一些代数量对图进行描述. 定义图G的加权邻接矩阵A=[aij]：当(i,j)∈E 时，aij=aji>0，否则aij=0. 对于任意i∈V，节点i的度定义为进一步，图的度矩阵定义为，图的Laplace矩阵定义为矩阵L是对称半正定矩阵，且L1N=0n. 而且，若图G是 连通的，则L仅有一个零特征值，其他特征值都为正数. 有关图论和代数图论的详细内容可以参考文献[19].

2 优化问题与分布式算法

本节首先描述分布式一致性最优化问题，然后给出求解该问题的分布式算法.

2.1 问题描述

考虑由N个个体组成的多智能体网络，其信息分享关系图为G=(V,E). 对于i∈V，个体i可以控制本地的决策变量xi∈Ωi，其中，Ωi⊂Rn是本地可行集合. 多智能体一致性控制问题，是指设计分布式的控制律，使得所有决策变量可以从初态收敛到某个相同的末态，即渐近满足x1=···=xN. 这里的分布式，是指仅允许从本地数据和网络邻居个体中获得信息来更新决策变量. 进一步，考虑每个个体都有一个关于决策变量的目标函数（成本函数或效用函数），记为fi(xi). 分布式一致性最优化问题，是希望设计分布式算法，使得多智能体网络不仅能够实现一致性，还能实现总体目标函数的最优性.

结合上述多智能体网络背景，分布式一致性最优化问题的数学描述为

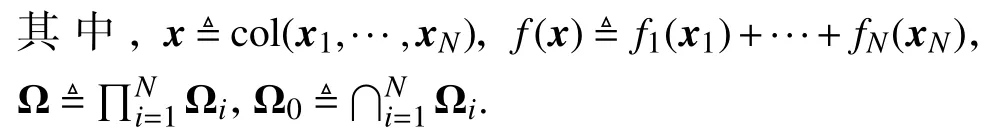
在求解问题（1）的过程中，假定每个个体i∈V的本地目标函数不能被全局共享或者被其他个体获取，而个体i能够根据本地数据获取目标函数在给定点的梯度值，但无法获取其他个体目标函数相关的任何信息.

下面给出问题（1）的基本假设条件.

假设1：对于每个i∈V，fi(xi)是可微凸函数，且∇fi(xi)是κf-Lipschitz连续的，其中κf>0为某个常数. Ωi是非空的闭凸集合. 并且，优化问题（1）至少存在一个有限的最优解.

假设2：图G是 一个连通图.

上述条件是最基本的，也常见于其他文献中.在假设1中，fi与Ωi的凸性保证问题（1）是一个凸优化问题.fi的可微性使得个体能够利用本地梯度信息进行寻优. 最优解集非空则确保了问题的适定性. 此外，假设2中的连通性使多智能体网络实现整体一致性和最优性成为可能.

注1：与文献[7]、[8]和[11]相比，本文的分布式优化的问题模型带有集合约束，所以具有更广的应用范围. 文献[4]考虑了集合约束，但仅对相同的约束情形进行了分析，即Ω1=···=ΩN. 而本文不需要该限制条件.

2.2 分布式算法

为了能够借助凸优化理论与算法对问题（1）进行求解，先将一致性等式约束x1=···=xN等价地转化为标准等式约束形式h(x)=0. 事实上，可以选取h(x)=L⊗Inx，其中L是图G的Laplace矩阵. 这是因为，在假设2的条件下，L⊗Inx=0nN当且仅当x1=···=xN. 于是，问题(1)的等价描述为

问题（2）是一个标准的约束优化问题，可以定义一个Lagrange函数

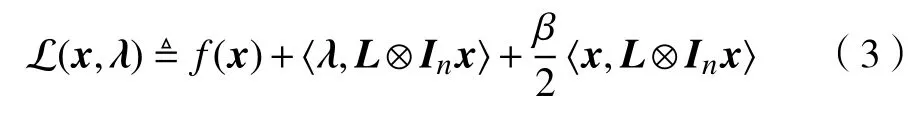
其中，λ≜col(λ1,···,λN)∈RnN为Lagrange乘子，β>0为一个常数. 通常也把x和λ分别称为原始变量和对偶变量. 在假设1的条件下，最优化问题（2）的一阶原始-对偶最优条件为

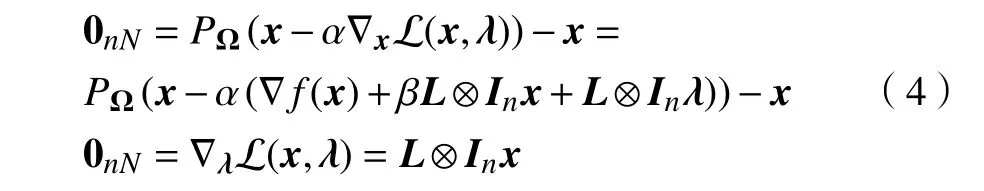
其中，α>0为任意常数.

根据最优条件（4），可以设计一个基于原始-对偶梯度的迭代算法：

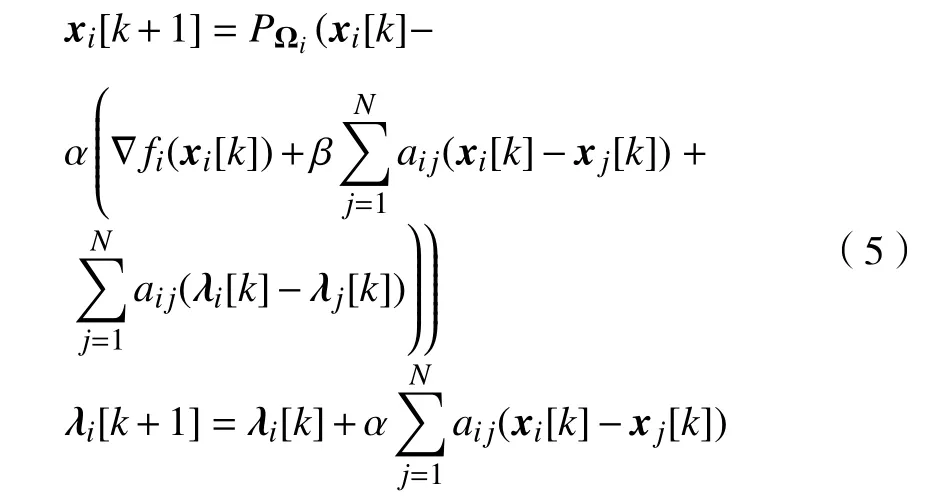
其中，常数α和β待定，它们将在收敛分析中根据收敛条件来确定. 算法（5）是一个分布式算法. 这是因为，个体i在更新xi和λi的过程中，仅利用了本地数据∇fi(xi)、Ωi、xi和λi，以及邻居个体的信息xj和λj.

将所有个体决策变量和对偶变量罗列起来，写成更紧凑的形式：

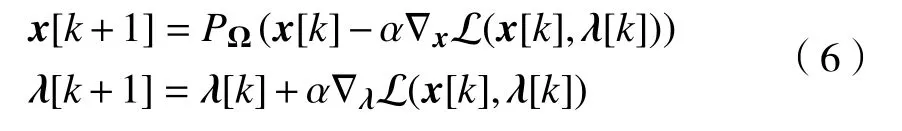
由式（6）可见，算法的设计上采用了求解L鞍点的梯度下降-梯度上升的方法. 其不动点满足一阶原始-对偶最优条件（4），从而确保了算法的正确性.

注2：文献[9-10]提出了类似的分布式原始-对偶梯度算法. 相比之下，本文考虑的算法具有两个可调参数：α和β. 因此，该算法更具灵活性，并且推广了文献中的算法.

3 收敛性分析

本节首先对一般的定步长迭代格式，提出基于李雅普诺夫函数的一种分析范式. 在此基础上，对本文的分布式算法进行分析，给出算法参数的选择范围.

3.1 基于李雅普诺夫函数的一种分析范式

考虑一般的迭代格式

其中F:Rm→Rm为连续映射，α>0为常步长. 集合Z 为迭代格式（7）的不变集，即z[k]∈Z,∀k≥0. 令为平衡点集合，这里假定Z∗不为空集.

为了分析论证迭代（7）的收敛性，本文提出一种基于李雅普诺夫函数的分析范式.

定理1：如果存在一个李雅普诺夫函数V:Rm×Rm→R满足：

1）对于任意的z∗∈Z∗，V(z,z∗)是正定的，即V(z,z∗)≥0，且V(z,z∗)=0⇔z=z∗；

2）对于任意的z∗∈Z∗，V(z,z∗)关于z是水平强制的，即对于任意的正数γ>0，V的水平集合有界；

3）对于任意的z∗∈Z∗，V(z,z∗)关于z可微，且映射∇zV(z,z∗)在z∈Z上 是κV-Lipschitz连续的，其中κV>0是一个常数；

4）存在某个常数δ>0，使得对于任意的z∗∈Z∗，都有，其中F(z)是（7）中的映射；

那么，由算法（7）产生的序列{z[k]}收敛到某一个平衡点，即存在某个满足

证明：任取z∗∈Z∗. 因为∇zV(z,z∗)是κV-Lipschitz连续的，有

3.2 分布式一致性最优化梯度算法的收敛分析

考虑分布式一致性最优化梯度算法（6）. 为了得收敛条件，采用上小节提出的基于李雅普诺夫函数的分析方法.

其中，

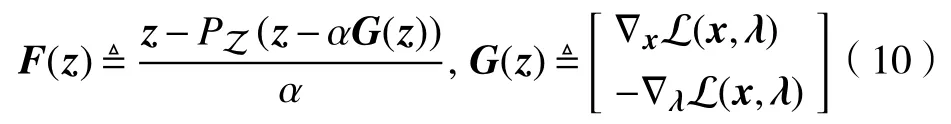
根据最优条件，映射G(z)满足

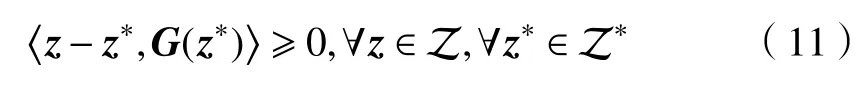
接下来，构造李雅普诺夫函数

由于L(x,λ∗)是关于x的凸函数，所以L(x,λ∗)−L(x∗,λ∗)−〈x−x∗,∇xL(x∗,λ∗)〉≥0. 于是，

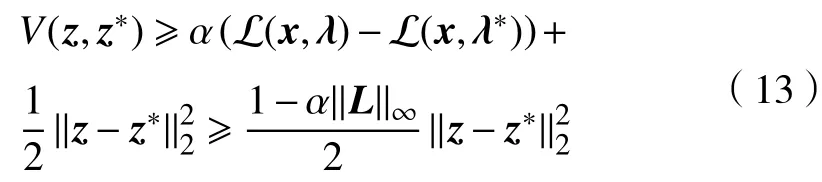
而且，V(z,z∗)是关于z的可微函数，可以通过计算得到

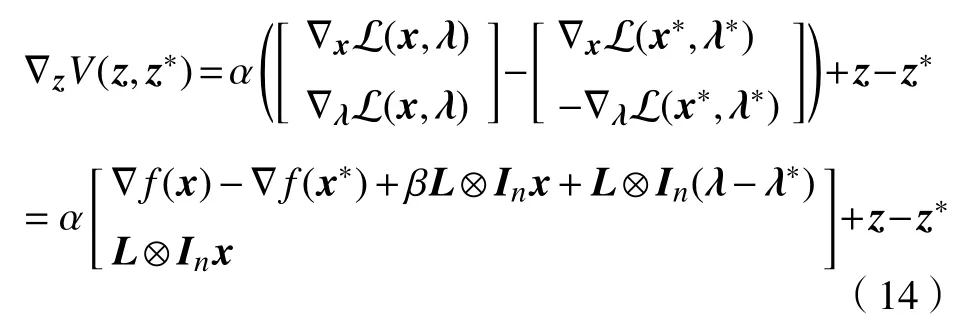
容易证明，∇zV(z,z∗)是关于z的κV-Lipschitz连续映射，其中

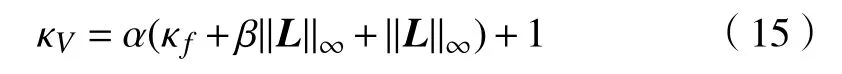
根据投影算子的基本性质和不等式(11)，容易证明

并且

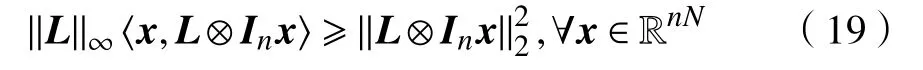
结合式（16）～（19），得到

至此，可以给出分布式算法（5）的收敛分析结果.

定理2：在假设1和假设2的条件下，如果分布式算法（5）的步长α和常数β满足

那么算法产生的迭代序列收敛到某个原始-对偶最优解.

证明：因为已经给出了定理1所述的基于李雅普诺夫函数的分析范式，所以这里仅需考虑式（12）构造的V(z,z∗)，并验证其满足各项条件.

首先根据（13），若0<α<1/‖L‖∞，则V(z,z∗)是正定的，也是水平强制的，即满足范式条件中的1）和2）. 然后，由（15）可知，V(z,z∗)满足条件3）. 再次，根据式（20），如果β≥2α‖L‖∞，则

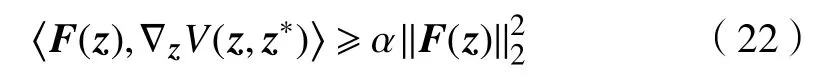
即V(z,z∗)满足条件4），且δ=α. 将范式条件5）及其他关于α和β的条件列在一起，得到

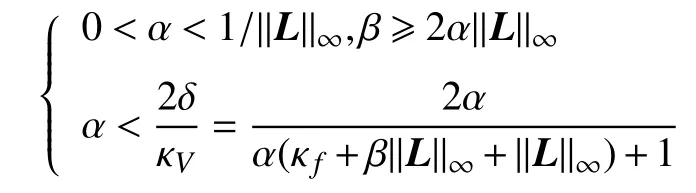
整理后即可得到式（21）中的参数条件.

证毕！

4 数值实验

本节给出一个数值算例来验证算法的有效性.

考虑优化问题（2），其中N=5，决策变量xi∈R，Ωi=[i−10,i−2]，i∈{1,2,3,4,5}. 每个个体的本地目标函数为

个体之间的信息分享关系如图1所示.

图 1 信息分享关系图Fig.1 Information sharing graph

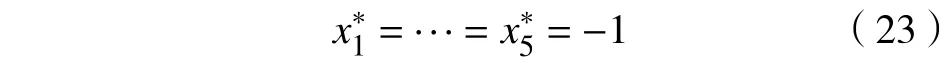
通过分析和计算得

因此，根据式（21），选择β=0.9，得到参数α的选择范围是0<α<0.075. 在数值实验中，选择α=0.07，得到的实验结果如图2～4所示. 可以看出，由于选择了合适的步长等参数，算法仅迭代300次后就已经收敛到最优解. 这些实验结果验证了本文提出的分布式算法及其收敛分析方法的正确性和有效性.

图 2 决策变量的更新轨迹Fig.2 Trajectories of decision variables

图 3 对偶变量的更新轨迹Fig.3 Trajectories of dual variables

图 4 李雅普诺夫函数的更新轨迹Fig.4 Trajectory of the Lyapunov function

5 结论

对分布式一致性最优化问题进行了研究，设计了具有两个可调参数的分布式原始-对偶梯度算法，并论证了算法的收敛性. 针对一般的定步长迭代格式，提出一种基于李雅普诺夫函数的分析范式，具有普适性和一般性，在收敛分析方面具有框架性和系统性. 提出的方法运用在论文所考虑的分布式梯度算法上，得到了算法收敛条件，确定出算法参数的选择范围，证实了方法的有效性. 给出的数值实验结果也验证了该方法的有效性. 接下来的工作将包括对其他类型的分布式优化算法进行设计和分析，如带有耦合等式或不等式约束的分布式资源分配问题等.