基于多目标支持向量机的ADHD分类

杜海鹏，邵立珍，张冬辉

北京科技大学自动化学院工业过程知识自动化教育部重点实验室, 北京 100083

注意力缺陷多动障碍（Attention deficit hyperactivity disorder, ADHD）是儿童期最常见的精神疾病之一，在大多数情况下持续到成年期. ADHD在DSM-5中被定义为神经发育障碍，主要表现为注意力缺陷，过度活动和行为冲动等症状[1]. 据报道，全球儿童和青少年中ADHD的发病率为3.4%.ADHD的病因和发病机制尚不清楚，目前ADHD的诊断主要依赖于医生的主观经验. 因此，ADHD的客观诊断和有效治疗是神经科学领域的重要课题之一.

近年来，脑电图[2]、磁共振成像[3]和功能性磁共振成像[4]等技术已被用于ADHD的辅助诊断.其中，静息态功能磁共振成像（Resting state functional magnetic resonance imaging, rs-fMRI）在精神疾病的病理分析中显示出其特有的优势，不仅可以用于诊断ADHD，还可以用于诊断精神分裂症[4]和老年痴呆症[5].

研究者们提出了各种特征提取、选择和分类方法用于基于rs-fMRI的ADHD分类中. Castellanos等[6]发现fMRI的功能连接信息可以成为ADHD诊断的一个突出特征. Du等[7]提出了一种判别子网络的方法来对ADHD进行分类，该方法挖掘了来自全脑网络的判别子网络，并使用基于图核的PCA来提取特征. Qureshi等[8]计算了fMRI的全局连通图，并利用基于图谱的皮质分割的平均连通性度量作为分层极限学习机分类器的输入特征. Miao和Zhang[9]提出了一种基于权重的relief算法来获得rs-fMRI中低频波动分数幅度的特征子集. Riaz等[10]集成了非影像数据和影像数据的机器学习框架，研究ADHD和正常受试者之间功能连接的改变. 考虑到数据不平衡性，合成少数类过采样技术（Synthetic minority oversampling technique，SMOTE）[11]用于生成少数类样本.

以上提到的大多数分类算法均假设样本是均衡的. 然而事实上，基于rs-fMRI的ADHD数据分类问题中数据集是不平衡的. 若采用传统的分类方法，通过不平衡学习会导致对多数类别样本的过度聚焦，分类器性能下降. 已有的不平衡数据处理方法大体分为两大类：数据层面的方法和算法层面的方法[12]. 数据层面的方法通过数据采样来处理数据不平衡问题，而算法层面的方法通常在决策过程中对不同的错分样本引入不同的惩罚因子. 在ADHD数据分类中，SMOTE方法已用于处理数据集不平衡问题. 但是，通过对少数群体/多数群体进行随机过采样/欠采样，这些创建平衡训练数据集的策略可能导致分类器性能欠佳[13].

考虑到分类问题的多目标性质，Shao等[14]提出了一种用于ADHD分类的双目标分类方法. 但是，该方法并没有考虑数据集的不平衡性. 因此，本文提出了采用基于SVM的多目标分类方案来解决ADHD数据不平衡问题，该方案通过多目标优化单独惩罚错分的正负样本，从而可以从算法层面有效地处理数据不平衡问题.

1 数据处理

本研究中使用的数据集来自于ADHD-200竞赛（http://fcon_1000.projects.nitrc.org/）[15]. 数据集主要从三个站点获取，分别是Kennedy Krieger Institute（KKI），New York University Medical Center（NYU）和Peking University（Peking）. 实验采用了五个数据集，分别为KKI，NYU和Peking-1，Peking-2和Peking-joint，其中Peking-joint由Peking-1，Peking-2和Peking-3三个数据集组成. 数据标签类型分为正常人群（Normal control, NC）和ADHD患者. 实验所用到的五个数据集的详细描述如表1所示.

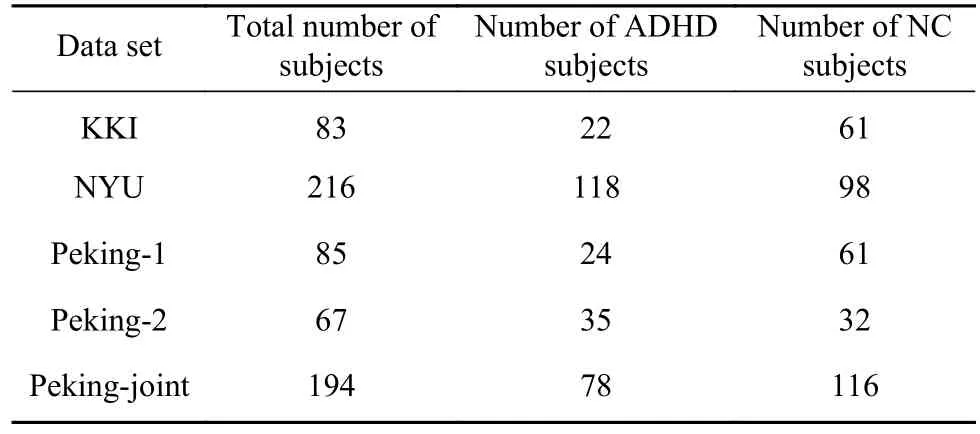
表 1 ADHD-200数据集描述Table 1 Description of ADHD-200 data sets

数据的预处理过程采用了DPARSF工具箱（http://rfmri.org/DPARSF）. 预处理主要包括移除前十张不稳定图像，时间层校正，头动校正，空间标准化，带通滤波和平滑处理. 接下来对90个脑区分别计算其平均时间序列值，进一步地计算90个脑区两两之间的皮尔逊相关系数，最终得到功能连接（Functional connection, FC）矩阵[16]，FC矩阵采集的流程图如图1所示. 由于FC的对称性，取下三角矩阵（(90×90−90)/2=4005）作为样本的特征.

由于实验所用数据集特征的个数远远大于样本个数，采用PCA（Principal component analysis）[17]对数据进行降维. 为了尽可能多地保留信息，每个数据集的特征维度降至比其训练样本的数量少1.

2 多目标分类方案

本文提出的基于多目标支持向量机的ADHD分类方案如图2所示. 首先建立三个目标分类模型，其次通过多目标优化算法求解多目标优化问题以得到帕累托（Pareto）最优分类器，然后评估分类器性能，在交叉验证集中选出最佳分类器，最后在测试集上进行测试.

2.1 三个目标SVM分类模型

在二分类问题中，数据集中每个类别下的样本数目相差很大，则该数据集被认为是不平衡的.数目少的一类称作少数类样本，数目较多的一类称为多数类样本. 文中所用数据集，多数类为NC样本，少数类为ADHD样本.

支持向量机（Support vector machine, SVM）是一种常用的有监督机器学习算法[18]. 给定一个具有m个 样本的训练集合S={(x1,y1),(x2,y2),···,(xm,ym)}，其中xi∈X⊂Rn表 示第i个样本的特征，yi∈{−1,+1}代表第i个样本的标签. SVM的基本思想是在特征空间上找到最佳的分离超平面使得训练集上正负样本间隔最大. 分类超平面可以用y=w·x+b表示，其中，w∈Rn表示法向量，b∈R表示截距.

图 1 功能连接矩阵采集流程图Fig.1 Flowchart of functional connection matrix acquisition

图 2 基于多目标支持向量机的ADHD分类方案Fig.2 ADHD classification scheme based on multi-objective SVM

传统的SVM对泛化能力和经验误差进行加权，它在本质上是一个双目标优化问题[19]. 文献[14]采用了基于1范数的双目标分类模型用于分类ADHD和NC受试者. 但是，该模型没有考虑不平衡数据分布，把正样本的误差和负样本的误差加和在了一起. 事实上，当存在类不平衡时，由于分类器的目的是最大化整体准确性，传统的分类器将倾向于多数类. 换句话说，分类器可能将所有样本分类为负值，从而提高过高的准确度.

本文使用如下三个目标SVM模型（T-SVM）对正负样本的误差成本分别进行处理，其中三个目标分别是最大化分类间隔，最小化正样本经验误差之和与最小化负样本经验误差之和[20].

其中，m+表示多数类样本个数，分别代表正负样本的经验误差，目标函数反映了最大化分类间隔的同时最小化正负样本的经验误差. 为使优化问题（T-SVM）可解，用两个正变量来表示w，即w=w++w−，因此第一个目标函数就表示为‖w‖1=eT(w++w−)，其中e是全为1的列向量. 该模型是一个多目标线性优化问题（Multi-objective linear programming, MOLP）. 基于多目标优化最优解的概念，本文给出如下Pareto最优分类器的定义.

2.2 多目标优化算法

本文采用法向边界交叉法(Normal boundary intersection method, NBI)[21]来求解MOLP问题.

其中，X={x∈Rn:g(x)=(g1(x),g2(x),···,gp(x))T≤0}代表决策变量可行域，假设其非空，则目标空间可行域为Y={f(x):x∈X}.

对于MOLP问题，如果不存在x∈X使得，则称∈X为MOLP问题的一个有效解. 有效解组成的集合表示为XE，称作决策空间中的有效集合. 相应地，称作一个非支配点，YN={f(x):x∈XE}称之为目标空间可行域中的非支配点解集. NBI方法就是为了求得MOLP问题中的非支配点集YN的子集R. 图3展示了NBI方法求解一个两个目标优化模型的示例. 该方法首先计算一个参考平面，并在参考平面上放置均匀分布的参考点，然后沿着法线方向将参考点投影到Y的边界，最终得到多目标优化模型的代表性非支配点集合R. 利用NBI解多个目标优化问题如算法1所示.

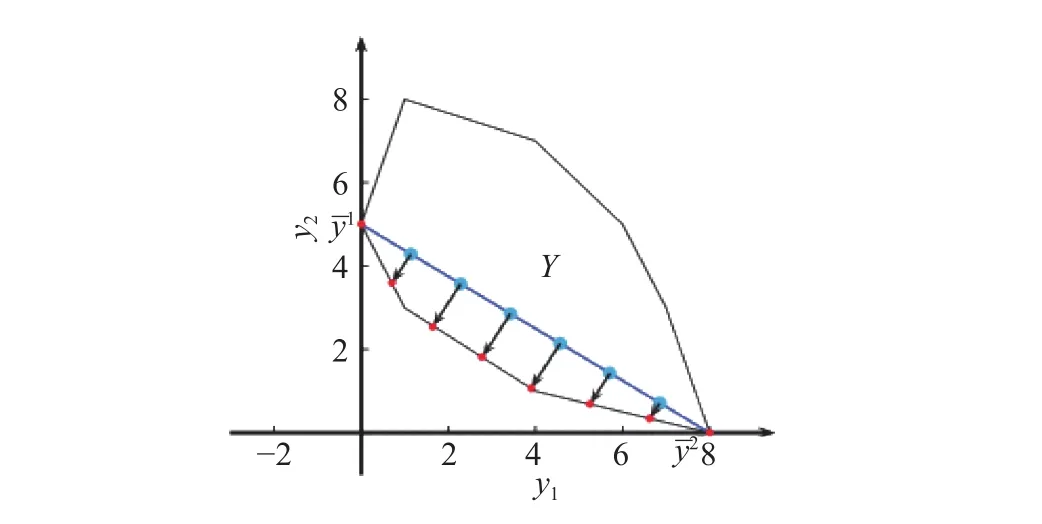
图 3 NBI方法中获得的非支配点Fig.3 Non-dominated points obtained using the NBI method

算法1 NBI算法求解MOLP问题

输入：优化问题模型

（2）在参考平面上布置均匀分布的参考点qi,i=1,···,k；

（3）遍历所有的k个参考点，求解最优化问题：

输出：代表性非支配点子集R

通过NBI方法可以求得一组MOLP的代表性非支配点. 对于（T-SVM）问题，每个非支配点都对应一个Pareto最优分类器. 决策者可以在交叉验证集上遍历所有的Pareto最优分类器，选择出性能最优Pareto分类器作为最终的分类器.

2.3 分类器性能评估

对于一组Pareto最优分类器，决策者需要根据交叉验证集上的性能选择最终分类器. 常用的衡量分类器性能的评价指标有灵敏度（Sensitivity）、特异性（Specificity）和准确性（Accuracy）. 敏感性表明少数群体的准确性，特异性表明多数群体的准确性.

一般情况下，准确率通常被视为评估标准之一. 但是，在数据集不平衡的情况下准确率不能完全反映分类器的性能好坏. 例如，对于正负样本比率为1∶9的数据集，即使判断所有少数类别的样本都错误，准确率仍然可以达到90%. 但是对于疾病诊断，正确分类少数类样本（患病）是很重要的.因此，本文使用灵敏度和特异性的几何平均值gmeans来评估分类器性能.

3 实验结果

本文使用提出的基于1范数SVM的三个目标分类方案对ADHD-200竞赛的五个数据集进行分类测试. 每个数据集都被随机分为三个数据集：训练集、交叉验证集和测试集，划分比例为6∶2∶2，即使用数据集的60%用于训练，20%用于模型交叉验证选取最终分类器，剩余的20%用来测试衡量最终分类器的效果.

下面以Peking-1数据集为例，给出分类器的选择过程. 首先，用NBI方法来求解由训练集构成的（T-SVM）问题，从而获得一组非支配点，共11个，如图4（a）所示，每个对应一个Pareto最优分类器，图中三个坐标轴分别代表分类间隔‖w‖1，正样本经验误差之和与负样本经验误差之和. 进一步地，计算出11个分类器在训练集和交叉验证集上的准确率和g-means值，见表2.

图 4 Peking-1数据集上非支配点集. （a）非支配点集；（b）非支配点1-5的权衡关系Fig.4 Non-dominated points on Peking-1 data set: (a) non-dominated points; (b) trade-off information of non-dominated points 1-5

表 2 训练集/交叉验证集上的性能评价Table 2 Evaluation of the training/cross-validation data set

为了清楚地展示非支配点三个目标之间的权衡关系，选取了前五个非支配点，在图4（b）和图5中展示其所对应的分类器的性能. 图4（b）展示了三个目标之间的权衡关系，可以看出随着‖w‖1的增加，正样本经验误差之和随之上升，而负样本经验误差之和随之下降. 图5进一步展示了这五个分类的性能，其中5（a）展示了分类误差，5（b）展示了g-means值. 两个子图中以菱形点绘成的曲线代表正样本的分类误差之和，图中具有相同横坐标值的其他点代表分类器在训练集与交叉验证集上的性能. 从图中可以看出，正样本（少数类）经验误差的减小是以牺牲多数类样本的准确性为代价的.

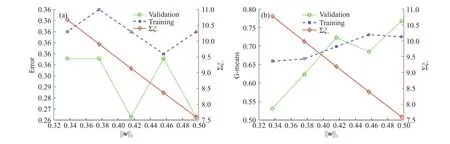
图 5 Peking-1数据集上1-5 Pareto最优分类器的性能.（a）范数与经验误差的关系；（b）范数与g-means的关系Fig.5 Performance of Pareto optimal classifiers 1-5 for Peking-1: (a) norm versus empirical error; (b) norm versus g-means

根据所有非支配点对应的Pareto最优分类器在交叉验证集的表现，对于Peking-1数据集，选择了具有最高g-means（值为0.7596）的分类器5作为该数据集的最终分类器. 其他几个数据集的处理过程与Peking-1数据集一样，由于篇幅限制这里不再给出.

为了进一步地展示本文提出的三个目标分类方案的性能，将本文提出的方法与1范数SVM（L1SVM）、2范数SVM（L2SVM）、随机森林（random forest, RF）[22]、极限学习机（extreme learning machine,ELM）[23]以及两个目标分类方案（B-SVM）进行了对比分析. 其中，L1SVM和L2SVM中的超参数C=0.8；RF中树的个数为50，每棵树的最大深度为5；ELM中隐层节点个数为30. 实验运行了十次，最终给出了每个数据集下十次的平均结果，如表3所示. 表中每个数据集最高的准确度以及最高的g-means值均以黑体加粗的形式给出. 对比结果表明，本文提出的三个目标的方案在所有ADHD数据集上的表现都优于其他对比方法.

除ADHD数据集外，本文也选取了University of California Irvine（UCI）Machine Learning Repository上的MNIST数据集来测试提出的方法的有效性.MNIST数据集有10类，我们对其进行下采样并随机选取标签为“9”的50个样本作为正样本，其他类均为负样本构造分类问题. 分类结果如表3所示，结果表明本文提出的方法对一般的不平衡数据集也具有较好的分类效果.

表 3 不同方法的平均准确度/g-means值Table 3 Average accuracy/g-means value for different methods

4 结论

本文提出了一种基于多目标支持向量机的ADHD数据分类方案. 该方案使用基于1范数SVM的三个目标优化模型，分别考虑了正负样本的经验误差，从而可以从算法层面有效地处理类不平衡问题. 通过求解多目标优化问题，可以得到一组代表性的Pareto最优分类器以供决策者进行选择. 该分类方案在ADHD-200数据集上进行了测试并和文献中的方法进行了对比分析. 实验结果表明，本文提出的三个目标SVM分类方案在所有测试数据集上的表现优于1范数SVM，2范数SVM，随机森林、极限学习机和双目标SVM方法.