基坑上跨既有盾构隧道坑底土体加固方式探究

2020-06-08施成华李翔雷明锋彭立敏

铁道科学与工程学报 2020年5期

施成华，李翔，雷明锋，彭立敏

施成华，李翔，雷明锋，彭立敏

(中南大学土木工程学院，湖南长沙 410075)

基于非线性接触理论，建立三维非连续地铁隧道模型。考虑管片接头之间、管片衬砌与围岩之间、螺栓与螺栓孔之间的相互作用，以及基坑施工全过程的影响，对基底纵向加固、横向抽条加固和格栅加固3种不同形式的加固措施在控制隧道整体竖向变形、管片接头混凝土应力、螺栓内力方面进行对比分析。研究结果表明：格栅加固效果最为理想。以此模型为基础，进一步研究隧道与基底加固区夹角与隧道隆起变形、接头混凝土应力的关系，得到最优隧道与基底加固区夹角应为2倍土体内摩擦角与45°之间。

盾构隧道；共线；管片接头模型；格栅加固；隧道与基底加固区夹角

随着城市化的不断发展，对已建成的地铁隧道上方进行基坑开挖的现象也越来越常见。基坑开挖引起的土体卸载会破坏下方既有地铁隧道的应力平衡，造成隧道整体隆起，变形较大处的管片接头、螺栓等破坏尤为明显，进而影响隧道结构及列车运营的安全。因此在既有地铁上方进行基坑开挖施工必须采取非常严格的变形控制措施。LIU等[1]采用三维黏弹塑性有限元数值计算方法，对临近隧道施工影响下既有隧道衬砌结构的受力状态进行了分析；梁荣柱等[2−5]将隧道−地层简化为Timoshenko- Winkler模型，得到了隧道变形曲线与附加应力的对应关系，可用于研究邻近基坑施工对既有隧道的影响。张治国等[6−7]运用有限元软件对深基坑开挖对邻近地铁产生的影响进行研究分析；刘波[8]通过对超深大基坑的信息化监测，研究了上海陆家嘴基坑邻近地层的时空位移特征，分析了深大基坑邻近地层的变形机理与影响因素；李瑛等[9]以三维数值模拟的手段，对基坑上跨既有地铁进行全过程分析，从施工工序以及加固方式上进行对比分析。SHI等[10]从基坑开挖对邻近既有地铁隧道的安全性在管片接头、螺栓应力等方面做了细致的研究分析。已有的研究虽然从隧道整体变形行为上分析了上方土体卸载带来的影响，但是缺乏管片接头、螺栓等细部结构的分析研究。本文以深圳桂庙路快速化改造工程为背景，研究明挖隧道与既有地铁共线段的地铁隆起变形控制问题，通过模拟施工全过程，从隧道整体变形行为、接头混凝土应力等方面出发，对比几类常见的基坑底部土体加固方式，并进行优化，为控制地铁隧道隆起提供参考。

1 工程简介

1.1 工程概况

桂庙路快速化改造工程实施范围西起规划振海路，止于后海滨路，道路全长约4.9 km，按城市快速路标准建设，主路为双向6车道加集散车道，地面辅路为双向6车道。工程建设的内容包括：隧道2座(振海路隧道和前海路至后海滨大道隧道)、现状立交改造1座(南海立交)、人行天桥、地面道路、市政管线、交通工程及其他附属设施。其中，振海路到南海立交段范围为地铁共建段，其余为非共建段。

共建段结构底板距离地铁盾构外轮廓8 m左右，地铁左右线均在开挖基坑内，既有地铁区间隧道与上跨基坑位置关系及地层条件如图2所示。

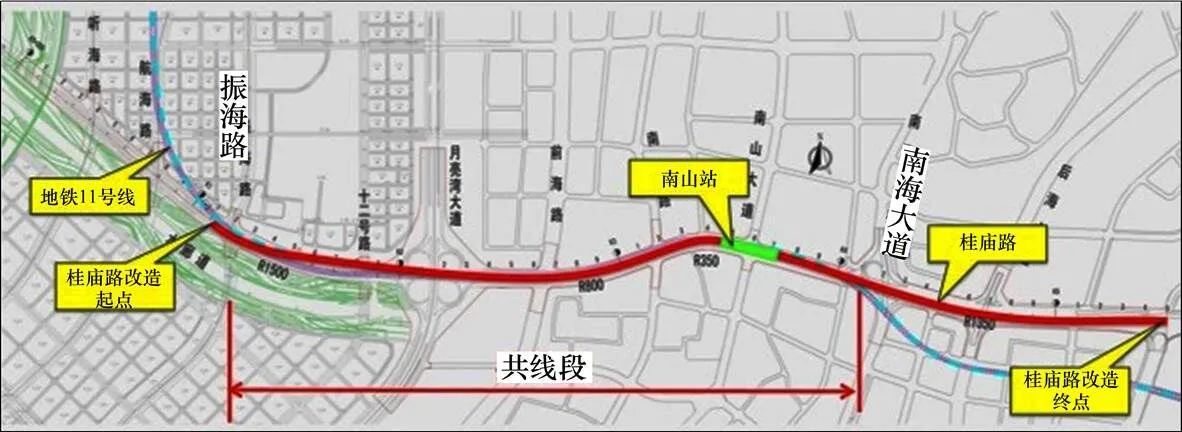
图1 桂庙路与地铁11号线的关系示意图

单位：cm

1.2 现场控制标准

地铁11号线采用装配式管片，过大的隆起差异变形必定会引起管片接缝张开量增大，造成渗漏水，重则导致管片破损，危及人民生命财产安全。故该工程中对既有隧道变形控制有以下几个控制标准：1) 地铁隧道的绝对变形量应不超过10 mm；2) 控制地铁隧道的差异变形不超过4 mm/10 m； 3) 水平收敛变形不应超过20 mm。

2 三维有限元非连续接触模型

2.1 模型建立及材料参数

本工程属于浅埋隧道，地应力场以自重应力为主，可不考虑构造应力。该模型主要针对桂庙路改造工程的K3+866~K3+966里程段，共计100 m。模型尺寸为长×宽×高=150 m×100 m×80 m，如图3所示。基坑底部距盾构隧道外缘8 m，基坑尺寸为长×宽×深=30 m×40 m×14 m，围护结构有1 m厚地下连续墙，1道混凝土支撑(截面1 m×1 m，间距4.5 m)，2道钢支撑(609 mm，=16 mm，水平间距2.2 m，竖向间距3.0 m)。既有地铁11号线隧道分块采用1个封底块K(17.5°)，2个邻接块(68.5°)和3个标准块(68.5°)，内外径分别为6 m与6.7 m，管段长1.5 m，接缝连接包括16个环缝螺栓和12个纵缝螺栓。

图3 三维有限元计算模型

模型钢支撑采用梁单元模拟，混凝土支撑采用实体单元进行模拟，螺栓尺寸依据M27高强螺栓确定，并考虑30 kN预紧力。围岩弹塑性采用Mohr- Coulomb本构模型，其余结构均采用线弹性本构模型[11]。各结构力学参数如表1所示。

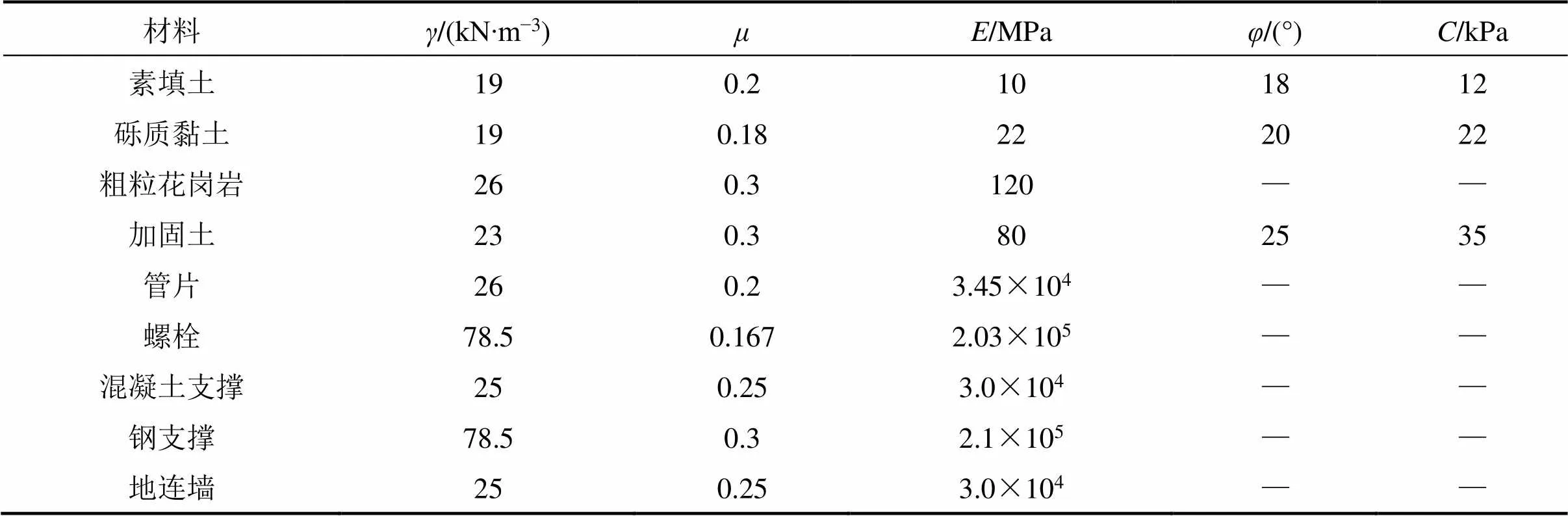
表1 地层及结构力学参数

2.2 接头及三维接触模型

为准确模拟衬砌管片接头的受力状态，运用AutoCAD和Hypemesh等对管片接头进行精确建模及前处理工作。建立包括螺栓孔、手孔及螺栓实体模型。如图4所示。

(a) 螺栓孔；(b) 螺栓细部模型

管片与管片、螺栓与螺栓孔之间的接触面法向行为采用“硬接触”，即2个物体在压紧状态下才会传递法向压力，一旦有空隙就不会传递应力，接触属性为惩罚刚度模型[12]：

式中：为接触法向压力；为嵌入量；k为接触面嵌入惩罚刚度；为惩罚函数，本文采用指数函数形式的罚函数。

接触面切向行为中，若接触面闭合，接触面定义为可传递摩擦力。本模型中，管片接头摩擦因数取0.62，螺栓孔摩擦因数取0.5。

管片与围岩接触对中，考虑到围岩力学参数较弱而不可避免出现接触面穿透的情况，通过设置接触法向刚度及最大允许过盈量来控制接触面穿透量，以上步骤在数值建模中实现。

该接触面切向行为中，依旧采用Coulomb定律计算，摩擦因数取0.88。

3 方案比选

3.1 计算工况

为研究基坑底旋喷桩加固区域形式的影响，设置3种工况，各工况下加固区域总体积保持不变，研究纵向加固与横向成条加固的效果差异，加固区范围与隧道相对位置如图5所示。

表2 各工况相关参数取值

为了更加贴近真实情况，模拟开挖工序按照“纵向分段、竖向分层”的原则，步长6 m，竖向分为4+4+4+2共4层，开挖方案示意图如图6所示，模型30 m范围内共计8个开挖步。考虑到模型计算效率问题，在基坑开挖影响范围外的隧道采用等效均质模型替代管片模型，刚度上取0.78的折减系数[12]。基坑开挖步与纵向位置关系如图6所示。

(a)基底纵向加固；(b)基底横向抽条加固；(c)基底格栅加固

图6 开挖工序示意图

3.2 纵向变形分析

各工况下的右线隧道轴线最终隆起曲线如图7所示。

图7 右线隧道轴线最终隆起曲线

间隔10 m的实测值为现场所布监测点的监测值，现场没有采取加固措施，最终隧道实测变形结果与模型无加固工况计算结果接近，可见该三维模型具备较高的准确度。

3种加固方案工况下隆起曲线最大值分别为8.61，8.36和7.61 mm，相比于无加固的11.16 mm，降幅达到20%~35%，可见对基坑底部进行加固是非常必要的。对比前2个工况，工况2有比较明显的变形控制效果。即在相同工程量的前提下，横向抽条加固在隧道隆起变形控制方面比纵向全幅加固效果好。

对比3个工况可知，格栅加固在控制隧道隆起变形方面效果最好，但由于本案例中基坑宽度达到40 m，基底格栅加固宽度亦为40 m，而既有隧道外径仅6.7 m，格栅加固的范围宽度尚可进一步优化。

3.3 管片接头应力分析

基底无加固工况下提取精细化管片整体变形图如图8(a)所示，可以发现，基坑处盾构隧道虽然呈整体上升趋势，但也可以划分为2种状态：精细化管片两端的“扁平段”和中心部分的“隆起段”。作最小主应力云图剖面图如8(b)所示，根据拱腰内侧是否受拉可知该2种状态的分界限分别为从前往后第13环与第25环。即管片从前往后第1~13和26~30环处于“扁平段”，第14~25环处于“隆起段”。对应到基坑范围为距基坑边缘6.5 m范围内均为“扁平段”，约为基坑长度的1/5。

(a) 右线隧道最终变形图；(b) 右线隧道最小主应力剖面图

分别选取“扁平段”、“隆起段”状态下管片接头压应力最大的环段：1号环与24号环。作出其接头处的混凝土压应力在3种基底加固方案下的图线如图9所示。

由图9(a)可知，在基坑两端的“扁平段”范围内，位于拱脚、拱底处的2号，1号，6号和5号接头压应力较大，且远离基坑中心线的2号接头压应力有最大值。对比3条折线，基底横向抽条加固和格栅加固能在一定程度上减小这6个接头的混凝土压应力，且拱脚和拱底接头压应力减小程度明显。综合来看，基底格栅加固效果更优。

由图9(b)可知，靠近基坑中心部分的“隆起段”管片接头混凝土压应力分布极不对称，远离基坑中心线的拱底4号接头混凝土压应力最大，拱腰处3号接头和拱脚5号接头压应力次之，拱顶1号和6号与靠近基坑中心的拱腰2号最小，基底加固后压应力分布趋势也基本一致。整体来看，纵向加固接头最大压应力为4.19 MPa，横向抽条加固接头最大压应力为4.51 MPa，格栅加固接头最大压应力为3.56 MPa，且分布较为均匀。

3.4 螺栓内力分析

该模型的螺栓内力从2个方面分析：纵缝螺栓和环缝螺栓。由于该模型下“扁平段”螺栓受力较小，故此处仅选取23号环与24号环之间的一组环缝螺栓与24号环内部的纵缝螺栓进行分析。环缝螺栓从顶部顺时针编号为1号~16号环缝螺栓，各基地加固方案下23号环与24号环之间环缝螺栓内力大小如图10所示。

单位：MPa

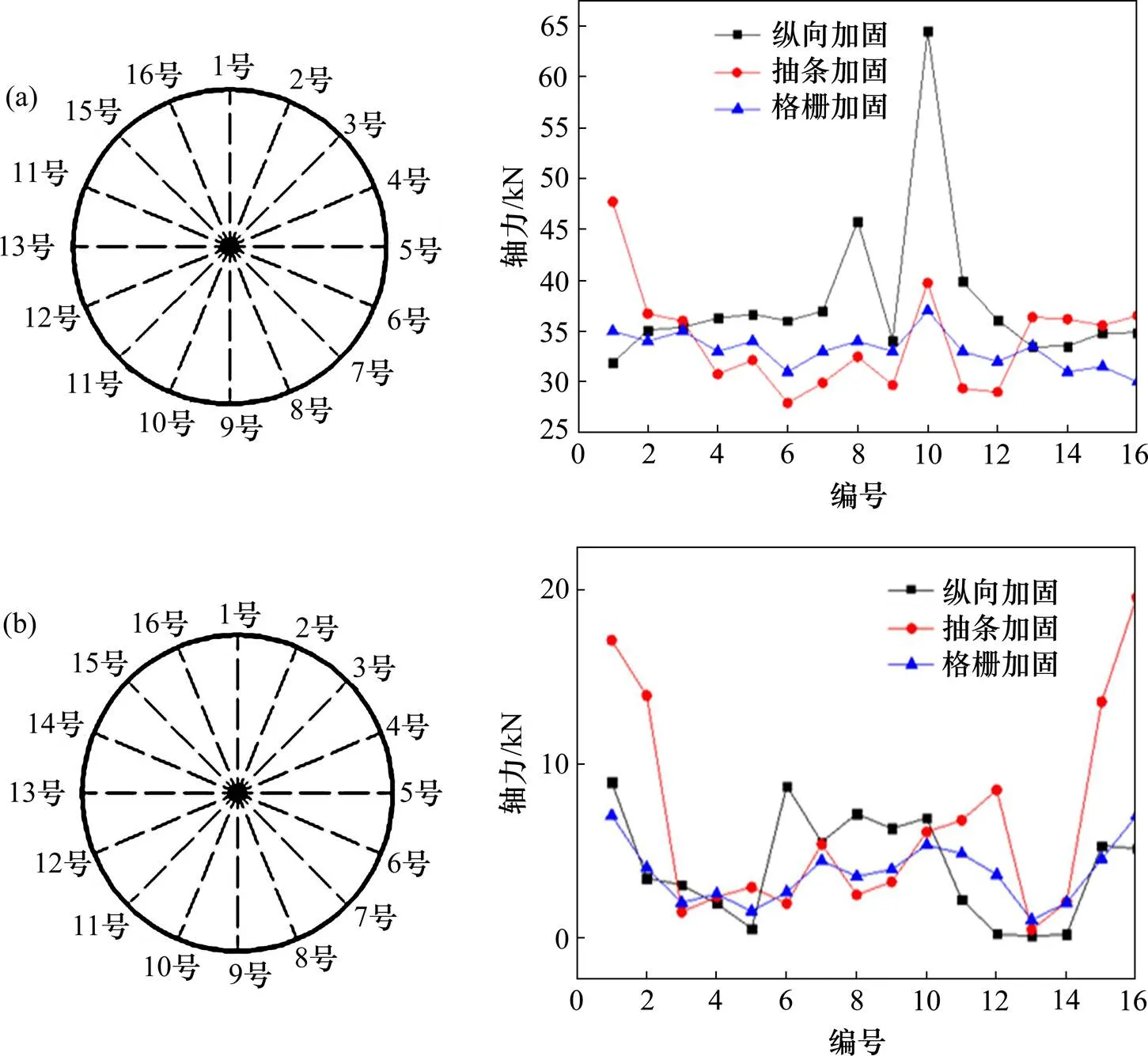
(a) 轴力；(b) 剪力

由图10(a)可知，基底纵向加固方案下，位于盾构隧道底部的环缝螺栓有较大的轴力，高达64.3 kN，明显大于抽条加固和格栅加固方案下的螺栓轴力。抽条加固和格栅加固方案下的环缝螺栓轴力各有高低，但总体较稳定在35 kN左右，相差不大。

由图10(b)可知，3种加固方案下环缝螺栓剪力分布趋势基本一致，即在隧道顶部和底部，环缝螺栓剪力较大，拱腰处剪力较小。明显发现基底抽条加固方案对控制隧道顶部环缝螺栓剪力效果较差，其螺栓剪力高达21 kN，近乎纵向加固和格栅加固螺栓剪力的2倍。

24号环纵缝螺栓内力如图11所示，由图11(a)可知，远离基坑中心的拱腰5号、拱脚4号纵缝螺栓轴力较大，3种加固方案下分布趋势基本一致。在5号纵缝螺栓处，横向抽条加固有比较明显的变化，轴力达到50 kN。纵向加固和格栅加固在纵缝螺栓轴力方面控制效果接近，各位置螺栓轴力相差不大，稳定在30~40 kN之间。

(a) 轴力(kN)；(b) 剪力(kN)

由图11(b)可知，远离基坑中心的拱腰5号和拱顶6号纵缝螺栓剪力较大，在抽条加固方案下有最大值6 kN，可见在环缝螺栓剪力控制方面，抽条加固效果不如纵向加固和格栅加固。

4 方案优化

综合前文分析可以看出，基底格栅加固在整体纵向变形、接头混凝土压应力、螺栓内力方面表现更优，但是上文模型中格栅加固范围宽度达40 m，尚有优化空间。提取基底无加固工况下的隆起曲线，其中峰值偏向既有隧道一侧，可见盾构隧道的存在影响着基坑底部土层的隆起变形大小[13]。相反，隧道上方一定范围内的围岩也会影响隧道的隆起变形，由此本文引入隧道与基底加固区夹角，用此角度来描述基底加固宽度、与隧道相对位置等关系[14]，如图12所示，可以更好地对比分析不同加固宽度对既有隧道隆起变形的影响。

图12 旋喷桩加固区域与隧道位置关系

通过三维混合数值模型求解，在保证相同基底加固工程量的前提下，各工况右线隧道隆起最大值及接头混凝土最大压应力如图13所示。

表3 加固区域宽度L取值

图13 隧道与基底加固区夹角α与隧道隆起最大值、接头应力最大值关系曲线

由图13可知，基底旋喷桩格栅加固宽度过小、过大，作用效果均较差，隧道隆起明显，接头混凝土压应力过大。格栅加固最优宽度应处在2tan2与2tan45°之间，即最优隧道与基底加固区夹角应为2倍土体内摩擦角与45°之间。

5 结论

1) 既有隧道上方基坑开挖会导致隧道整体隆起，最大隆起量达11.16 mm，已经超过该项目既定的10 mm绝对变形控制值，基底加固十分必要。距基坑边缘1/5范围内的隧道处于“扁平段”，中间部分变形为“隆起段”。2种形态下隧道结构受力变形完全不同，应分开进行分析。

2) “扁平段”管片混凝土接头应力最大值位于拱脚和远离基坑中心的拱腰处。“隆起段”管片混凝土接头应力最大值位于远离基坑中心的拱脚处，分布趋势基本一致，但在接头混凝土压应力控制方面，格栅加固最优，纵向加固最差。

3) 在螺栓受力方面，纵向加固对控制环缝螺栓剪力以及纵缝螺栓轴力、剪力大小方面，效果与格栅加固相近，且优于抽条加固。抽条加固在环缝螺栓轴力方面表现更好。总体来看，纵向加固和抽条加固各有优劣，但都不及格栅加固。

4) 基底格栅加固宽度过大过小均会造成隧道变形、接头混凝土应力增大。最优隧道与基底加固区夹角应处在2倍土体内摩擦角与45°之间。

[1] LIU H Y, Small J C, Carter J P, et al. Effects of tunnelling on existing support systems of perpendicularly crossing tunnels[J]. Computers and Geotechnics, 2009, 36(5): 880−894.

[2] 梁荣柱, 林存刚, 夏唐代, 等. 考虑隧道剪切效应的基坑开挖对邻近隧道纵向变形分析[J]. 岩石力学与工程学报, 2017, 36(1): 223−233. LIANG Rongzhu, LIN Cungang, XIA Tangdai, et al. Longitudinal deformation analysis of adjacent tunnels due to excavation of foundation pits considering tunnel shear effect[J]. Journal of Rock Mechanics and Engineering, 2017, 36(1): 223−233.

[3] LIANG Rongzhu, XIA Tangdai, HUANG Maosong, et al. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect[J]. Computers and Geotechnics, 2017(81): 167−187.

[4] LIANG R, WU W, YU F, et al. Simplified method for evaluating shield tunnel deformation due to adjacent excavation[J]. Tunnelling & Underground Space Technology, 2018(71): 94−105.

[5] 梁荣柱, 夏唐代, 胡军华, 等. 新建隧道近距离上穿对既有地铁隧道纵向变形影响分析[J]. 岩土力学, 2016, 37(增1): 391−399. LIANG Rongzhu, XIA Tangdai, HU Junhua, et al. Analysis of the influence of the close-up of the new tunnel on the longitudinal deformation of the existing subway tunnel[J]. Geomechanics, 2016, 37(Suppl 1): 391−399.

[6] 张治国, 张谢东, 王卫东. 临近基坑施工对地铁隧道影响的数值模拟分析[J]. 武汉理工大学学报, 2007(11): 93−97. ZHANG Zhiguo, ZHANG Xiedong, WANG Weidong. Numerical simulation analysis of influence of adjacent foundation pit construction on subway tunnel[J]. Journal of Wuhan University of Technology, 2007(11): 93−97.

[7] 李伟强, 孙宏伟. 邻近深基坑开挖对既有地铁的影响计算分析[J]. 岩土工程学报, 2012, 34(增1): 419−422. LI Weiqiang, SUN Hongwei. Calculation and analysis of influence of adjacent deep foundation pit excavation on existing subway[J]. Journal of Geotechnical Engineering, 2012, 34(Suppl 1): 419−422.

[8] 刘波. 上海陆家嘴地区超深大基坑邻近地层变形的实测分析[J]. 岩土工程学报, 2018, 40(10): 1950−1958. LIU Bo. Field measurement and analysis of deformation of adjacent stratum of super deep and large foundation pit in Lujiazui area of Shanghai[J]. Journal of Geotechnical Engineering, 2018, 40(10): 1950−1958.

[9] 李瑛, 陈金友, 黄锡刚, 等. 大面积卸荷对下卧地铁隧道影响的数值分析[J]. 岩土工程学报, 2013, 35(增2): 643−646. LI Ying, CHEN Jinyou, HUANG Xigang, et al. Numerical analysis of the effect of large-area unloading on the underlying subway tunnel[J]. Journal of Geotechnical Engineering, 2013, 35(Suppl 2): 643−646.

[10] SHI Chenghua, CAO Chengyong, LEI Mingfeng, et al. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints[J]. Tunneling and Underground Space Technology Incorporating Trenchless Technology Research, 2016(51): 175−188.

[11] SHI Jiangwei, Ng C W W, CHEN Yonghui. Three- dimensional numerical parametric study of the influence of basement excavation on existing tunnel[J]. Computers and Geotechnics, 2015(63): 146−158.

[12] 艾辉军. 基于三维非连续接触模型的管片与接头结构力学特性研究[D]. 长沙: 中南大学, 2014. AI Huijun. Structural and mechanical properties of segment and joint based on three-dimensional discontinuous contact model[D]. Changsha: Central South University, 2014.

[13] 周俊宏, 宫全美, 周顺华. 基于透明土的隧道上浮过程结构与土相互作用模型试验[J]. 华东交通大学学报, 2016, 33(3): 1−6. ZHOU Junhong, GONG Quanmei, ZHOU Shunhua. Model test of interaction between structure and soil during tunnel uplift based on transparent soil[J]. Journal of East China Jiaotong University, 2016, 33(3): 1−6.

[14] 曾英俊, 杨敏, 熊巨华, 等. 双线盾构长距离穿越深基坑底部引起地下连续墙沉降分析及控制措施[J]. 建筑结构学报, 2012, 33(2): 135−141. ZENG Yingjun, YANG Min, XIONG Juhua, et al. Settlement analysis and control measures of diaphragm wall caused by double-line shield tunneling long distance through the bottom of deep foundation pit[J]. Journal of Architectural Structures, 2012, 33(2): 135−141.

Study on reinforcement method for foundation pit of existing shield tunnel under foundation pit

SHI Chenghua, LI Xiang, LEI Mingfeng, PENG Limin

(School of Civil Engineering, Central South University, Changsha 410075, China)

Based on the nonlinear contact theory, a three-dimensional discontinuous subway tunnel model was established, which considered the interaction between segment joints, interaction between the segment and the surrounding rocks, and the interaction between the bolt and the bolt hole as well as the influence of the whole process of excavation construction.Contrast and analysis were made on controlling the whole vertical deformation of tunnel, the stress of segment joint concrete and the internal force of bolts based on three different reinforcement measures, i.e. longitudinal reinforcement, transverse strip reinforcement and grid reinforcement.The results show that the grid reinforcement effect is the optimal solution. On the basis of this model, the relationship between the width and diffusive angle of grille reinforcement and the deformation of tunnel uplift and the stress of joint concrete is further studied.The optimum diffusion angle should be between the 2 times the friction angle in the soil and 45 degrees.

shield tunnel;collineation; segment joint model; grille reinforcement; diffusion angle