基于集对可拓与三角模糊数的列控运营安全风险评估
2020-06-08王瑞峰吝天锁张振海
王瑞峰,吝天锁,张振海
基于集对可拓与三角模糊数的列控运营安全风险评估
王瑞峰,吝天锁,张振海
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
针对现有列控运营安全评估方法不足,以及列控运营过程中的复杂性与不确定性等问题,将集对分析和物元可拓理论引入其风险评估中。以影响列控运营安全的列控设备、环境和更新改造等6个主要因素建立评估指标,利用三角模糊数确定列控运营指标权重,并构建集对可拓耦合的列控运营评估模型,通过耦合模型的综合联系隶属度评估列控运营风险。研究结果表明:该列控系统运营风险为低度风险,且模型能够真实反映列控运营安全风险评估中的不确定性,可以帮助风险管控部门对运营风险提前预判,保证列车安全运行。
集对可拓;三角模糊数;列控运营;风险评估
随着我国高速铁路和客运专线的大规模建设与开通,我国高铁未来将逐步从“建设施工阶段”进入“运营维护阶段”,运营和维护的需求日益增大。对于列控运营系统而言,我国当前的重点工作是选择合适的评估方法,利用运营风险数据库中积累的风险因素数据,对其运营风险的不确定性进行研究,进一步提高运营风险提前预判水平。可见对列控运营风险新评估方法的研究将成为各大院校及科研院所的重点研究课题之一。目前,对高速铁路系统的安全管理和安全评估已有很多评估方 法[1−3],但对列控系统运营安全风险评估的方法略显不足。主要有云模型[4]、三维矩阵[5]和多级可拓评估法[6]等。云模型可以较好的处理不确定性系统的模糊性和随机性,但是未考虑风险趋势的转化问题。三维矩阵是在风险矩阵的基础上演化而来,也存在风险矩阵的通病[7]。多级可拓评价法无法解决待评物元体中的元素超出节域的情况,其在列控运营风险评估中有一定的局限性,无法准确体现系统的不确定性。针对以上问题,本文采用集对分析与物元可拓理论耦合的方式。集对分析法是处理不确定性系统随机性和模糊性问题的一种新方法,通过同异反的分析,可处理列控运营风险的转化问题,结合物元可拓理论从定性与定量分析列控运营安全的特点,构造两者的集对可拓耦合评估模型,并将该模型首次应用到列控运营安全风险评估中,以期对列控运营安全进行更加全面的分析。
1 列控运营安全风险评估体系与权重
1.1 列控运营安全评价指标体系
列控运营安全的风险评价,国内外主要采用的是EN 50126中的风险矩阵方法[8],在此基础之上,根据文献[6]建立的列控运营安全评估指标,只针对一级指标主要影响因素进行分析,如图1所示。

图1 列控运营风险评估体系
1.2 评估指标权重确定
现有的列控运营指标权重主要采用主观赋权的方式,为提高其评估的准确性,利用模糊层次分析法[9−10]计算各评估指标的权重,以三角模糊数确定指标重要程度,具体计算过程如下。
假设评估指标Z和Z分别为评价指标集对应的第,个指标(,,=1,2,…,6);比较评价指标Z和Z,可得到两者的三角模糊数r;与之对应的最小值、特征值和最大值分别表示为a,b和c。评价指标重要程度判断准则如表1所示。
根据表1中列控运营评价指标重要程度的判断准则,然后两两比较确定其重要性,用三角模糊数表示其重要程度,从而得到模糊判断矩阵=(r)6×6。
根据矩阵,可得到评价指标Z和其他指标的模糊判断程度(Z)为

同理,可得到指标集Z的总模糊判断程度()为

因此,评价指标Z和其他指标的模糊综合程度F为


表1 评价指标重要程度判断准则
若评价指标Z大于其他指标重要程度,则可能度向量(Z)为

则式(4)对应的三角模糊数可能度为:

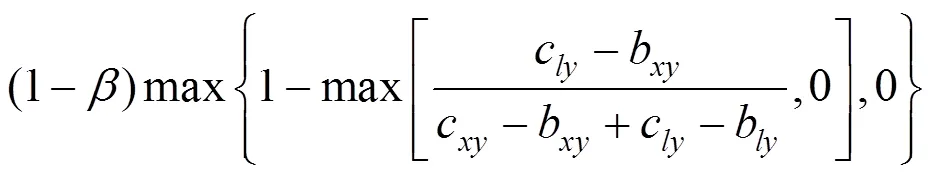
式中:表示决策者对列控运营风险控制系数,且取值范围为[0,1],当<0.5时,表示决策者对风险持积极态度;当0.5时,为中立;当>0.5时,为消极。本文取0.5。
评价指标集的可能度矩阵为
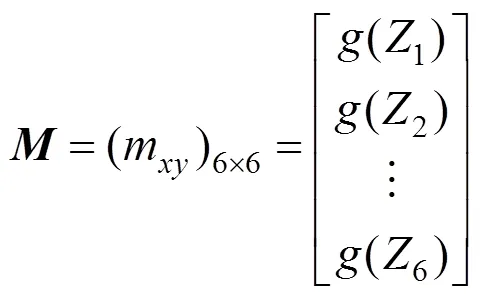
评价指标Z的权重为

则权重向量=(1,2,…,6),归一化处理后,得到评价指标集的权重向量为=(1,2,…,6)。
2 集对可拓耦合模型建立
2.1 物元可拓基本理论
物元理论可参考文献[11],本文不再介绍。具体分析如下:若事物以个特征1,2,…,和相应的量值1,2,…,v描述,则
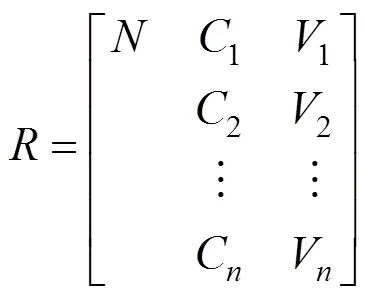
式中:,和分别为评价对象、评价指标和指标量值,通常以三元组=(,,)作为基本元。
依据物元理论,设评估对象={1,2,…,N} (=1, 2, …,)为总样本集合,C为第(=1,2,…,)个特征。选取N为评估对象,则V为特征C的量值范围,所以构造的经典域为
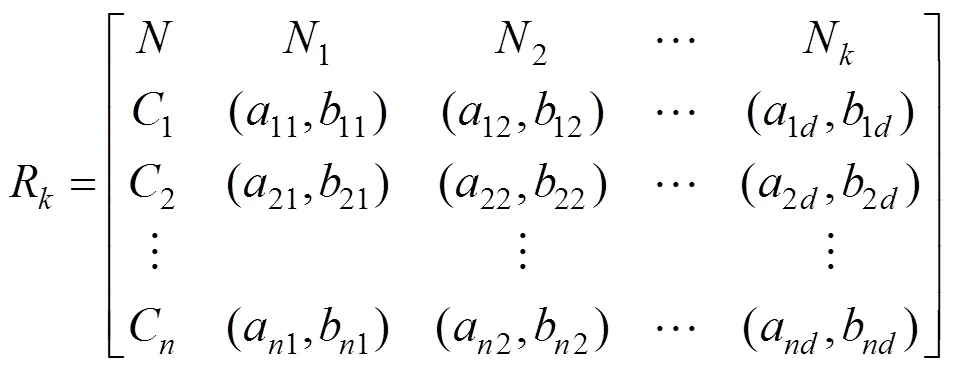
相对应C的节域为

式中:(a,b)为评价指标对应的量值范围。
结合构造的经典域和节域,可得到整体的同征物元体R(=1,2,…,)为
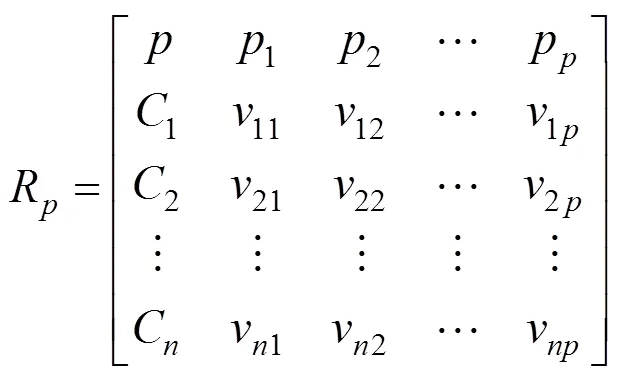
2.2 基于集对可拓构建联系隶属函数
集对分析[12−13]是基于一分为三原理对构成集对的2个集合间关系进行同异反分析,整体处理确定和不确定性的相互作用和转化关系。可拓理论[14]从定量关系和空间形式扩展到事物的性质、特征和向量,并从各个角度对系统进行客观地分析,两者具有一定的共性。以列控运营实际得到的指标量值与标准的评估等级构成集对,然后与可拓集合论域进行耦合[15],对应关系如图2所示。
根据集对分析和可拓理论,分析图2可知:若比较待评估指标C的实测值x和评估等级(=1,2,…,)且x位于内,可用SPA同一性描述两者关系,也可用可拓集合标准正域0=(F,F+1)表示其数值范围。因此,可得到如下的联系隶属关系
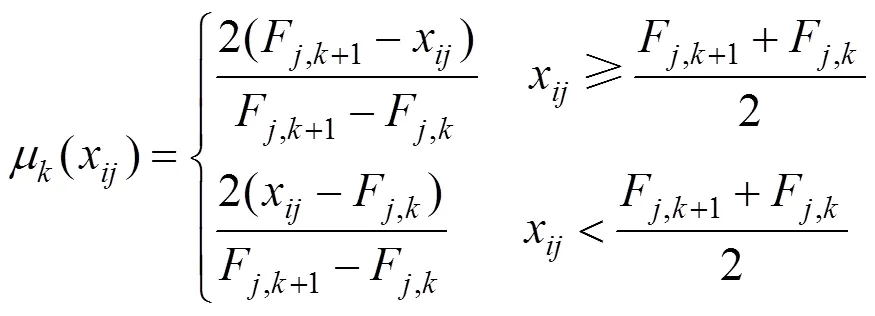
式中:Fj,k和Fj,k+1分别为评估等级k的左右界限值;μk(xij)为待评估对象i对评估等级k中的指标j形成的标准正域的联系隶属度,且μk∈(−1,1)。
若比较待评估指标C的实测值x和评估等级(=1,2,…,)且x位于相邻−1(>2)或(+1)等级内,用SPA差异性和可拓集合过渡正域1=(F−1,F)或2=(F1,F2)表示。其联系隶属关系如下

其中


式中:F,k和F,分别为讨论等级的左右界限值;(x,0)和(x,)分别为样本指标C的实测值与评估标准等级中构成的可拓正域和标准正域的距。式(15)中,当1时,F,k−1取F,k;而当时,F,k+2取F,k。
若比较待评估指标C的实测值x和评估等级(=1,2,…,)不满足以上两者规定,则用SPA对立性表示,此时联系隶属度μ(x)=-1。
风险评估等级可由综合联系隶属度μ来同等反映,结合权重可求其综合联系隶属度,如式(16)所示,对应的评估等级见表2。


表2 评估标准等级
2.3 评估流程
基于以上理论和模型,设计评估流程如下。
1) 采用现场调研,对某路局列控运营情况综合考评,确定风险评估指标和风险等级。

图3 列控运营风险评估流程
2) 根据该路局的调研结果,构造评估物元,根据物元可拓理论得到各个评估指标的经典域和 节域。
3) 依据SPA的同异反理论与可拓理论分析研究对象,并构建相应的联系隶属度函数。
4) 利用三角模糊数确定各评估指标的权重值。
5) 根据步骤3和步骤4确定的综合联系隶属度对风险等级进行判定。评估方案流程如图3所示。
3 实例分析
3.1 实际运营概况
以某高速铁路记录的某列控运营数据库中得到定量指标,以及相关部门记录的综合考评记录得到定性指标,并结合专家经验,从而得到样本数据见表3。
3.2 经典域与节域确定
根据6个主要风险指标的大数据统计状况,综合分析后按照均分(最高评分为100)的方法划分为4个评估等级,具体见表4。

表3 列控运营风险评估指标实测值
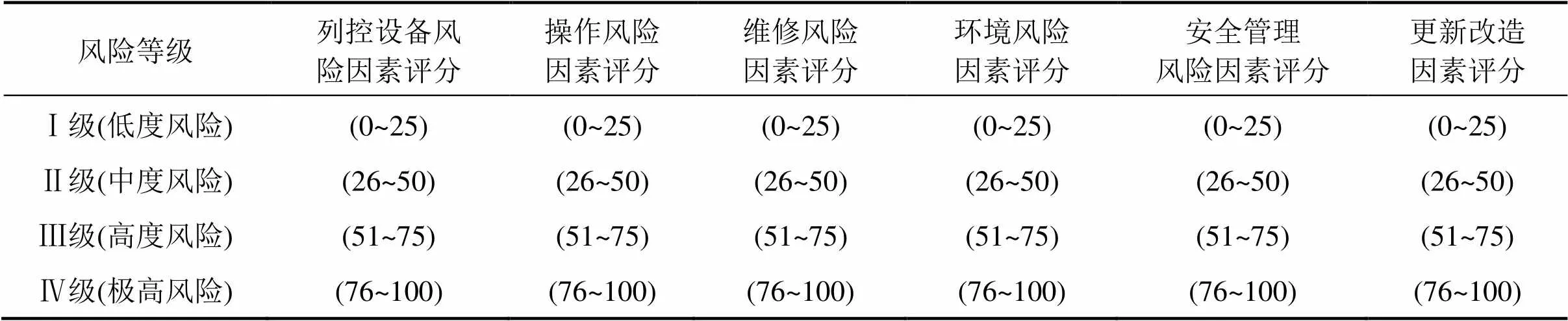
表4 评价指标分类标准
因此,列控运营风险评估指标经典域R如下:

同理,列控运营风险评估指标节域如下:
因此,列控运营风险评估整体的评估同征物元体R为
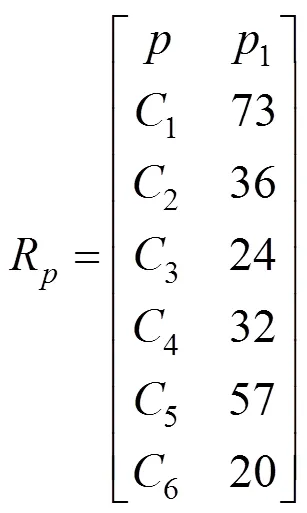
3.3 确定联系隶属函数
根据集对可拓耦合模型图2以及式(12)~(15)可得各指标的联系隶属度,以第1组数据为例。



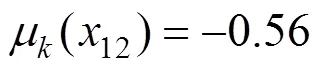


3.4 指标权重的计算
邀请列控运营维护、风险管控等方面的专家,根据表1对指标集=(1,2,3,4,5,6)进行比较,得到风险评估指标集的三角模糊判断矩阵为

由式(1)~式(3)可得评价指标的综合重要程 度为:
由式(4)~(7)可得指标权重,结果如表5所示。

表5 评价指标权重
3.5 列控运营安全风险等级确定
根据式(16)求出该列控系统的运营风险的综合联系隶属度μ=-0.623 8,计算另外2组数据得到的联系隶属度分别为-0.665 4和-0.604 4,根据表2的标准评估等级,3组数据同时验证该列控系统运营风险等级为Ⅰ级(低度风险)。根据实地调研发现由于列车车次较多,操作人员的一些不规范操作,上次考评结果为低度风险,模型分析结果与实际运营情况相符。
3.6 模型评估方法对比
在评价指标体系和指标权重不变的基础上,利用文献[4]提出的云模型方法和文献[6]提出的多级可拓评价法对本文方法进行对比验证。生成的标准云和综合云模型如图4所示,为低风险;计算多级可拓方法的综合关联度为(−0.158 7(低),−0.095 4 (中),−0.488 1(高),−0.213 6(极高))根据最大隶属原则,为中风险,对比结果如表6所示。

图4 标准云与综合评价云
通过对比发现,云模型和集对可拓模型的评估结果与实际情况更加相符,也更加验证了集对可拓模型对列控运营安全风险评估的准确性与实用性。为现场的风险评估提供了一种新方法。

表6 评估模型对比
4 结论
1) 建立基于集对分析与物元可拓原理耦合的集对可拓模型,从系统的角度分析列控运营安全风险,较好的处理了列控运营过程中的确定性与不确定性的关系,并且评估模型清晰客观,计算过程 简单。
2) 基于三角模糊数确定权重的方法比以往主观权重的方法更加客观,降低了专家评估打分的主观性,使列控运营安全风险指标权重更加准确,且可真实反映评估样本。
3) 根据实例的分析结果验证了集对可拓评估模型在列控运营安全风险评估中的可行性。说明本模型可对列控运营提供风险预判,及时提出防控措施,减少事故发生频次,保障列车安全运营。
[1] 刘超, 唐涛, 李开成. 高速铁路信号系统的安全管理评价研究[J]. 中国安全科学学报, 2013, 23(1): 129−135. LIU Chao, TANG Tao, LI Kaicheng. Safety management evaluation of high-speed railway signal system[J]. Chinese Journal of Safety Sciences, 2013, 23(1): 129− 135.
[2] 刘敬辉, 戴贤春, 郭湛, 等. 铁路系统基于风险的定量安全评估方法[J]. 中国铁道科学, 2009, 30(5): 123− 128. LIU Jinghui, DAI Xianchun, GUO Zhan, et al. Quantitative risk-based safety assessment method for railway systems[J]. China Railway Science, 2009, 30(5): 123−128.
[3] 马艳霞, 郑云水, 马兵, 等. 基于可拓学的铁路信号系统安全风险评价[J]. 控制工程, 2019, 26(3): 525−531. MA Yanxia, ZHENG Yunshui, MA Bing, et al. Safety risk assessment of railway signal system based on extenics[J]. Control Engineering, 2019, 26(3): 525−531.
[4] 郭荣昌, 陈光武, 赵小娟. 基于云模型和不确定AHP的列控运营安全评估[J]. 铁道学报, 2016, 38(11): 69− 74. GUO Rongchang, CHEN Guangwu, ZHAO Xiaojuan. Train control operation safety assessment based on cloud model and uncertain AHP[J]. Journal of the China Railway Society, 2016, 38(11): 69−74.
[5] 郭荣昌, 赵小娟, 张振海. 列控运营风险评价的三维矩阵模型研究[J]. 铁道学报, 2017, 39(5): 78−83. GUO Rongchang, ZHAO Xiaojuan, ZHANG Zhenhai. Research on three-dimensional matrix model of train control operation risk assessment[J]. Journal of the China Railway Society, 2017, 39(5): 78−83.
[6] 张亚东, 郭进, 戴贤春, 等. 基于多级可拓评价法的列车运行控制系统运营安全风险评价[J]. 中国铁道科学, 2013, 34(5): 114−119. ZHANG Yadong, GUO Jin, DAI Xianchun, et al. Operation safety risk assessment of train operation control system based on multi-level extension evaluation method[J]. China Railway Science, 2013, 34(5): 114− 119.
[7] 吴穹, 张春艳. 三维危险评价方法的探讨[J]. 沈阳航空工业学院学报, 1994(2): 47−51. WU Qiong, ZHANG Chunyan. Discussion on three- dimensional risk assessment method[J]. Journal of Shenyang Institute of Aeronautical Technology, 1994(2): 47−51.
[8] EN 50126, Railway application-the specification and demonstration of reliability, availability, maintainability and safety[S].
[9] 苏哲斌. 基于一致性逼近的三角模糊数互补判断矩阵的排序方法[J]. 模糊系统与数学, 2009, 23(4): 126− 130. SU Zhebin. Ranking method of triangular fuzzy number complementary judgement matrix based on consistency approximation[J]. Fuzzy Systems and Mathematics, 2009, 23(4): 126−130.
[10] 杨妮, 张友鹏, 王思华. 基于AHP和比较可能度关系的列控车载系统安全可靠性分析[J]. 安全与环境学报, 2017, 17(5): 1676−1680. YANG Ni, ZHANG Youpeng, WANG Sihua. Safety and reliability analysis of train control vehicle-mounted system based on AHP and comparative probability relationship[J]. Journal of Safety and Environment, 2017, 17(5): 1676−1680.
[11] 左静. 基于物元可拓性的物元可拓域[J]. 郑州工业大学学报, 2001(3): 51−52. ZUO Jing. Matter element extension domain based on matter element extensibility[J]. Journal of Zhengzhou University of Technology, 2001(3): 51−52.
[12] 蒋云良, 赵克勤. 集对分析在人工智能中的应用与进展[J]. 智能系统学报, 2019, 14(1): 28−43. JIANG Yunliang, ZHAO Keqin. Application and progress of set pair analysis in artificial intelligence[J]. Journal of Intelligent Systems, 2019, 14(1): 28−43.
[13] WU A, MA Z, ZENG G. Set pair fuzzy decision method based on cloud model[J]. Chinese Journal of Electronics, 2016, 25(2): 215−219.
[14] 汪明武, 周天龙, 叶晖, 等. 基于联系云的地下水水质可拓评价模型[J]. 中国环境科学, 2018, 38(8): 3035− 3041. WANG Mingwu, ZHOU Tianlong, YE Hui, et al. Extensive evaluation model of groundwater quality based on Lianyun[J]. China Environmental Science, 2018, 38(8): 3035−3041.
[15] 何忠明, 刘可, 付宏渊, 等. 基于集对可拓粗糙集方法的高边坡爆破施工安全风险评价[J]. 中南大学学报(自然科学版), 2017, 48(8): 2217−2223. HE Zhongming, LIU Ke, FU Hongyuan, et al. Safety risk assessment of high slope blasting construction based on set pair extension rough set method[J]. Journal of Central South University (Natural Science Edition), 2017, 48(8): 2217−2223.
Safety risk assessment of train control operation based on set pair extension and triangular fuzzy number
WANG Ruifeng, LIN Tiansuo, ZHANG Zhenhai
(School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
In view of the insufficiency of existing train control operation safety assessment methods, as well as the complexity and uncertainty in the process of train control operation, set pair analysis and matter element extension theory were introduced into its risk assessment. The evaluation index was established by six main factors which affected train control operation safety, such as train control equipment, environment, renewal and transformation. The weight of train control operation index was determined by triangular fuzzy number. A train control operation evaluation model with set-pair extension coupling was constructed. The risk of train control operation was evaluated by the comprehensive connection membership degree of the coupling model. The results show that the operational risk of the train control system is low risk, and that the model can truly reflect the uncertainty in the safety risk assessment of the train control operation. It can help the risk management department to predict the operational risk in advance and ensure the safe operation of the train.
set pair extension; triangular fuzzy number; train control operation; risk assessment

TN929.5
A
1672 − 7029(2020)05 − 1105 − 08
10.19713/j.cnki.43−1423/u.T20190771
2019−09−02
国家自然科学基金资助项目(61763025)
王瑞峰(1966−),女,内蒙古卓资人,教授,从事列控系统研究;E−mail:784703662@qq.com
(编辑 蒋学东)
