现代有轨电车无砟轨道列车荷载取值研究

2020-06-08孙魁冯青松

铁道科学与工程学报 2020年5期

孙魁，冯青松

现代有轨电车无砟轨道列车荷载取值研究

孙魁，冯青松

(华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013)

为确定现代有轨电车无砟轨道的设计轮载和常用轮载的具体取值，根据轮轨相互作用原理，建立现代有轨电车-无砟轨道垂向耦合动力学计算模型。详细分析不同行车速度下车轮扁疤和美国6级线路不平顺谱对轮轨垂向力的影响，并比较上凸型和下凹型钢轨焊缝不平顺所引起的轮轨接触力变化规律的不同之处，同时也对轮轨垂向力数据进行统计分析，从而得到设计轮载和常用轮载的取值。研究结果表明：在车轮扁疤激励下，轮轨垂向力和动载系数随着行车速度的增加，呈现先增大后减小的趋势；下凹型钢轨焊缝不平顺对轮轨相互作用力的影响较大，而上凸型钢轨焊缝不平顺对轮重减载率的影响较显著；与钢轨焊缝不平顺相比，车轮扁疤对轮轨相互作用力的影响更大，因此在有轨电车车辆的日常养护维修过程中应及时对车轮扁疤进行维修；建议现代有轨电车无砟轨道的设计轮载和常用轮载分别取为静轮载的1.45倍和1.25倍。

现代有轨电车；无砟轨道；设计轮载；常用轮载；统计分析

现代有轨电车因具有舒适性好、振动噪声污染小和适应性强等突出优点，在国内的发展较为迅速。而且与传统城市轨道交通相比，现代有轨电车的全生命周期成本较低，可以有效地缓解中小型城市所面临的交通拥堵问题[1−2]。在进行高速铁路无砟轨道设计时，设计轮载和常用轮载分别取为静轮载的3倍和1.5倍。然而现代有轨电车在我国的发展刚刚起步，目前关于现代有轨电车无砟轨道关键设计参数尚无相应的规范可以参考。因此，亟需基于车辆−轨道耦合动力学原理开展有轨电车无砟轨道关键设计参数的研究。国内外学者围绕高速铁路无砟轨道动力学进行了大量的研究工作[3−7]。李斌等[8]以我国高速铁路有砟轨道为研究对象，选取扣件刚度和道床刚度为随机变量，借助蒙特卡洛法对轮轨力的概率分布特性进行研究，提出了不同行车速度下设计轮载的建议取值；蔡成标等[9]从车辆−轨道耦合动力学的角度针对高速铁路无砟轨道中的设计轮载、轨道刚度和路基不均匀沉降限值等关键设计参数进行了详细的研究；杨荣山等[10]选取Ⅰ型板式轨道的CA砂浆损伤为研究对象，综合运用理论研究和现场试验分析了CA损伤对车辆−轨道大系统动力特性的影响，并基于分析结果提出了CA砂浆损伤的限值；高亮等[11]借助UM软件建立了精细化的重载铁路车辆−轨道耦合动力学计算模型，详细分析了曲线地段的线路参数对轮轨系统动力响应的影响；邓永权等[12]建立了有轨电车−嵌入式轨道空间耦合动力学模型，选取轮重减载率作为评价指标确定了钢轨焊缝不平顺的限值。通过上述文献综述可知，目前关于现代有轨电车无砟轨道列车荷载取值的研究尚未见报道。因此，开展有轨电车−无砟轨道耦合动力学研究，并确定无砟轨道列车荷载取值具有重要的工程意义。本文以现代有轨电车长枕埋入式无砟轨道为研究对象，基于轮轨耦合动力学原理建立100%低地板有轨电车−无砟轨道垂向耦合动力学计算模型。首先，分析不同行车速度下车轮扁疤对轮轨垂向力的影响，并引起轮轨接触力的区别。然后，选取美国6级线路不平顺谱为输入激励，研究常规行车速度下轮轨垂向力的变化规律，并对轮轨垂向力数据进行统计分析。最后，综合考虑动力学分析结果和实际工况提出现代有轨电车无砟轨道设计轮载和常用轮载的建议取值。

1 有轨电车−无砟轨道耦合计算模型

1.1 现代有轨电车车辆模型

本文选取典型的100%低地板有轨电车车辆为研究对象，该车由4个模块组成，其中2节车为一组，整列车共2组，每节车体的中部正下方都安有转向架。车体与车体间通过铰接装置使4节车的地板面贯通，每节车辆之间上、下铰接各一个，并全部设置在车体间的中间位置，上部铰接为转动铰，下部铰接为固定铰，如图1所示。

图1 车辆编组示意图

在有轨电车车辆模型中，车体和转向架均具有沉浮、伸缩和点头3个自由度，轮对具有沉浮和伸缩2个自由度，故单节有轨电车车辆共有10个自由度。同时，将固定铰简化为垂向和纵向的大刚度弹簧−阻尼单元，以限制车辆与车辆之间在垂向和纵向上的相对位移，而将转动铰简化为纵向的大刚度弹簧−阻尼单元，以限制车辆与车辆之间在纵向上的相对位移[13]。现代有轨电车的车辆动力学计算参数如表1所示。

1.2 长枕埋入式无砟轨道模型

长枕埋入式轨道结构从上至下主要包括：60R2槽型钢轨、扣件、混凝土长轨枕和轨道板等部分，如图2所示。

表1 有轨电车车辆动力学计算参数

图2 长枕埋入式无砟轨道示意图

在长枕埋入式无砟轨道结构中，60R2槽型轨采用基于欧拉梁理论的梁单元进行模拟，扣件采用离散的弹簧−阻尼单元进行模拟，为了提高计算效率，轨道板采用壳单元进行模拟，下部的基础则采用均布的弹簧−阻尼单元进行模拟。无砟轨道结构的计算参数如表2所示。

1.3 轨道不平顺

由于国内目前尚无有轨电车无砟轨道不平顺谱的相关规定，但考虑到高速铁路的建造技术也引入到城市轨道交通领域，从而使得无砟轨道的铺设质量得到了大幅提高，故本文选取美国6级线路轨道不平顺谱作为轮轨系统的输入激励。轨道不平顺波长范围取为0.01~50 m，列车运行速度取为70 km/h，则对应的频率范围为0.39~1 944.44 Hz。当轨道不平顺波长大于1 m时，采用美国6级线路轨道不平顺谱；当波长小于1 m时，则采用短波不平顺谱，如式(1)所示：

式中：()为高低不平顺功率谱密度函数，mm2/m−1；为空间频率，m−1。

表2 长枕埋入式无砟轨道结构计算参数表

采用较为常用的三角级数法生成线路高低不平顺样本，如图3所示。

图3 高低不平顺样本

1.4 轮轨接触模型及动力系统求解

轮轨之间的垂向相互作用采用非线性赫兹接触理论进行模拟[13]，计算公式如式(2)所示：

式中：为轮轨接触挠度系数，m/N2/3；为车轮与钢轨之间的相对位移；为车轮滚动圆半径。

根据上述理论，建立的有轨电车−长枕埋入式无砟轨道垂向耦合动力学计算模型，如图4所示。

图4 现代有轨电车−无砟轨道垂向耦合计算模型

采用有限元法对车辆和轨道结构分别进行离散，从而得到车辆−轨道耦合系统的动力学方程，即：

本文借助ANSYS/LS-DYNA软件编制计算程序进行车辆−轨道耦合系统的动力学分析[14]。

1.5 模型验证

为了验证本文所建立车辆−轨道耦合动力学计算模型的正确性，将本文计算结果与文献[2]中的现场测试结果进行对比，如表3所示。分析表3可知，本文所建立模型得到的钢轨和轨道板的垂向加速度与文献[2]中的测试结果吻合良好，从而证明了本文所建立计算模型的正确性。

表3 计算结果与测试结果对比

2 设计轮载的动力学研究

设计轮载是在综合考虑了车轮扁疤和钢轨焊缝不平顺对轮轨作用力的放大作用之后所采用的无砟轨道结构设计荷载[15]。因此，本节将分别分析车轮扁疤和钢轨焊缝不平顺对轮轨相互作用力的影响。

2.1 车轮扁疤的动力学分析

车轮扁疤主要分为新擦伤和旧擦伤，而新擦伤在出现之后将会迅速发展为旧擦伤，故本文选取车轮旧擦伤进行研究。旧擦伤可以采用余弦函数进行描述，如式(5)所示[16]：

参考《铁路技术管理规程(TG/01—2014)》中的相关规定，车轮扁疤长度取为40 mm。由参考文献[3]可知，车轮扁疤引起的轮轨冲击力存在一个临界速度，其计算公式如式(6)所示：

式中：cr为车轮扁疤的冲击临界速度；1和2分别为车辆一系簧上和簧下质量；为重力加速度。

根据式(6)和式(7)可计算得到本文采用车辆所对应的临界速度约为30 km/h。故车辆运行速度分别取为20，30，40，50，60和70 km/h，将车轮扁疤不平顺引入到车辆−轨道耦合计算模型中进行分析，导向轮的轮轨垂向力计算结果如表4所示。

表4 轮轨垂向力极值及动载系数

通过表4可以看出，随着有轨电车行车速度的增加，轮轨垂向力极值和动载系数先增加后减小；当行车速度为30 km/h时，轮轨垂向力极值和动载系数取得最大值，这与文献[9]中的分析结果相同，从而证明了本文分析结果的正确性。故车轮扁疤引起的最大轮轨相互作用力为静轮载的1.45倍。

2.2 钢轨焊缝不平顺的动力学分析

钢轨焊接接头处的不平顺一般由波长1 m左右的较长波叠加波长0.1 m左右的较短波所形成，如式(8)所示[12]：

式中：为列车运行时间；为列车运行速度；1和2分别为较长波和较短波的波幅；为较短波波长。

在钢轨焊缝不平顺的动力学分析过程中按不利情况进行考虑，取较长波的波长和波幅分别为1 m和0.1 mm，取较短波的波长和波幅分别为0.1 m和±0.1 mm[12]，波幅为正则为上凸型钢轨焊缝不平顺，波幅为负则为下凹型钢轨焊缝不平顺。根据文献[17]可知，钢轨焊缝不平顺激励下轮轨垂向力与行车速度成正比。因此，本文运行速度取为70 km/h，即有轨电车最高运行速度，不考虑常规轨道不平顺的影响，则钢轨焊缝短波不平顺所引起的轮轨之间相互作用力如图5所示。

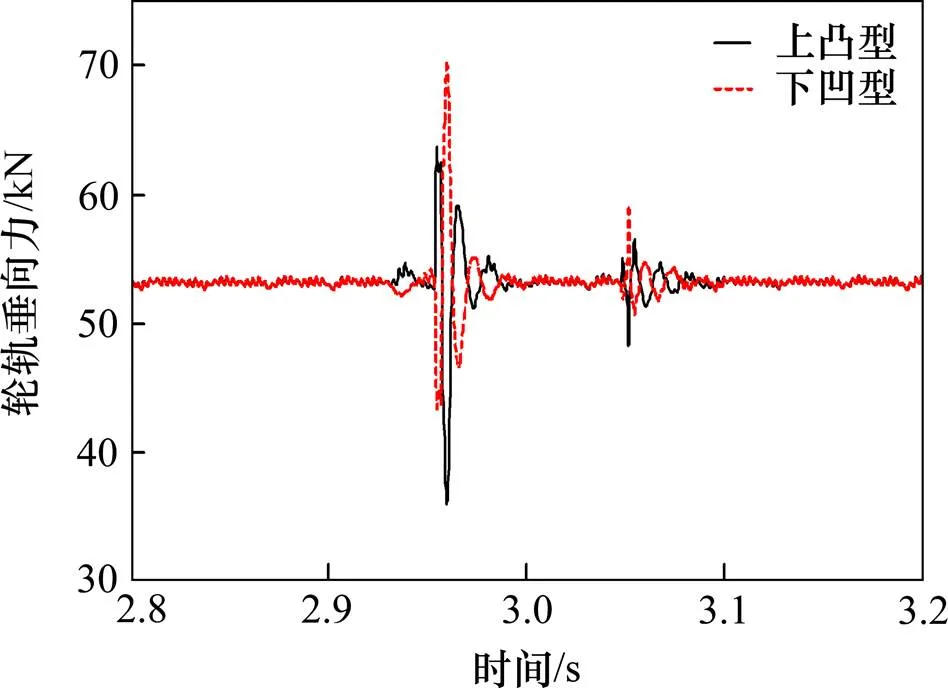
图5 钢轨焊缝不平顺引起的轮轨垂向力

由图5可知，上凸型和下凹型钢轨焊缝不平顺所引起的轮轨垂向力最大值分别为63.63 kN和70.22 kN，则动轮载系数分别为1.17和1.29，从而说明下凹型钢轨焊缝不平顺对轮轨相互作用力的加剧更显著。同时，上凸型和下凹型钢轨焊缝不平顺所对应的轮重减载率分别为0.34和0.19，表明上凸型钢轨焊缝不平顺对行车安全性的影响更大。

通过上述分析可知，当有轨电车的行车速度分别为40 km/h和70 km/h时，车轮扁疤和钢轨焊缝不平顺所对应的动轮载系数分别为1.45和1.29，故建议现代有轨电车无砟轨道的设计轮载取为静轮载的1.45倍。同时可以看出，与钢轨焊缝不平顺相比，车轮扁疤对轮轨相互作用力的影响更大，因此在有轨电车车辆的日常养护维修过程中应及时对车轮扁疤进行维修。

3 常用轮载的动力学研究

在进行无砟轨道结构设计时，一般取轮轨力数据的1~3倍标准差加上平均值作为常用轮载。在无实测数据时，也可以借助车辆−轨道耦合计算模型得到轮轨之间的相互作用力，然后对其进行统计分析，从而得到常用轮载[14]。

在动力学分析过程中，有轨电车行车速度分别取为50，60和70 km/h，只施加随机不平顺，不考虑车轮扁疤和钢轨焊缝不平顺的影响，导向轮的轮轨垂向力时程曲线如图6所示。

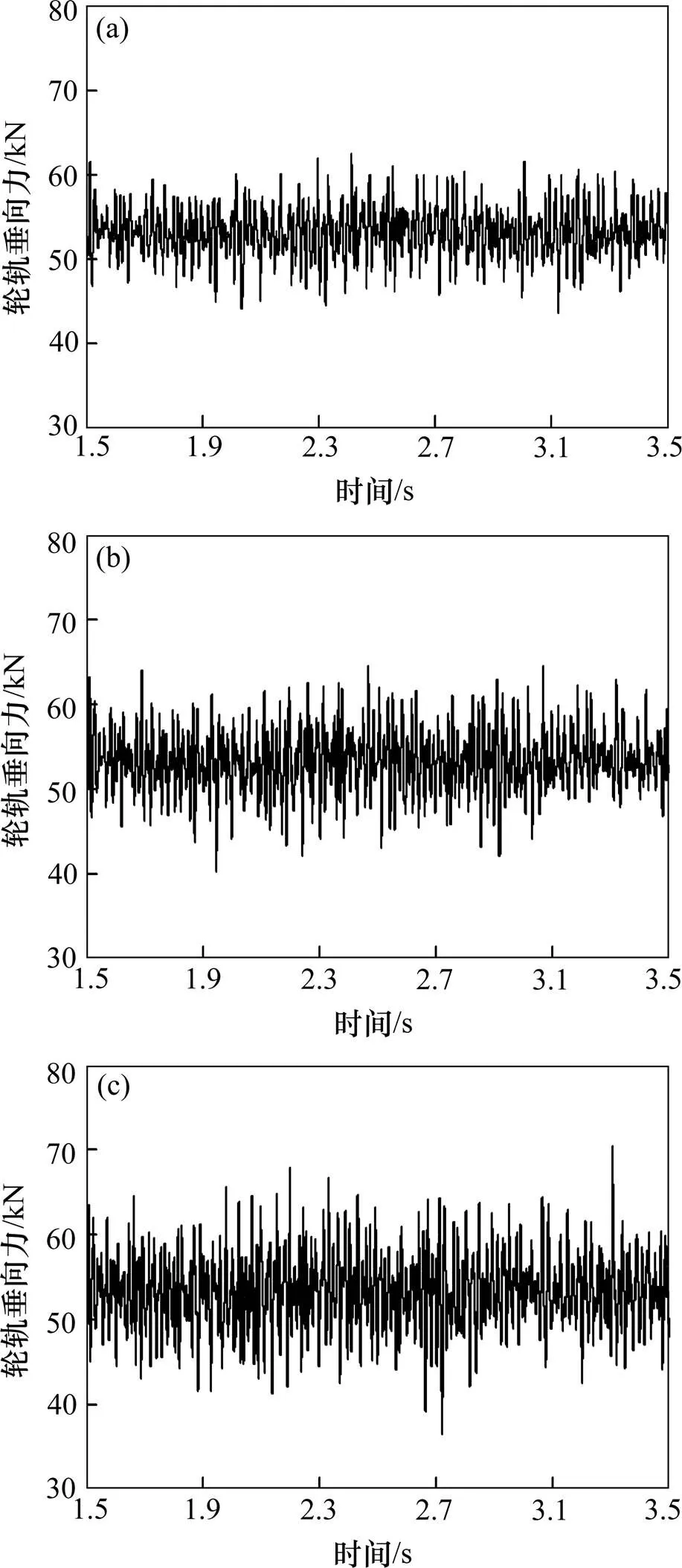
(a) 行车速度为50 km/h；(b) 行车速度为60 km/h；(c) 行车速度为70 km/h

分析图6可知，随着有轨电车行车速度的增加，轮轨垂向力呈迅速增大趋势；当行车速度从50 km/h增加到70 km/h时，轮轨垂向力最大值也随之从62.24 kN增加到69.75 kN，从而说明行车速度对轮轨垂向力的影响较为显著。

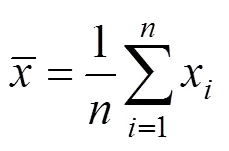
式中：为轮轨垂向力的样本总数；x为第个样本值。轮轨垂向力的统计分析结果如表5所示。

表5 轮轨垂向力的统计分析结果

由表5可知，随着行车速度增加，轮轨垂向力的均值基本保持不变，而轮轨垂向力的标准差显著性增加。当分别按1倍，2倍和3倍的标准差进行考虑时，常用轮载的动载系数分析结果如表6所示。

表6 常用轮载的动载系数

分析表6可知，当有轨电车的行车速度为70 km/h时，按1倍，2倍和3倍的标准差进行考虑所得的常用轮载动轮载系数分别为1.06，1.14和1.23，在考虑一定的安全系数的基础之上，建议现代有轨电车无砟轨道的常用轮载取为静轮载的1.25倍。

4 结论

1) 在车轮扁疤激励下，轮轨垂向力和动载系数随着行车速度的增加，呈现先增大后减小的趋势；当行车速度为30 km/h时，轮轨垂向力和动载系数均取得最大值。

2) 下凹型钢轨焊缝不平顺对轮轨相互作用力的影响较大，而上凸型钢轨焊缝不平顺对轮重减载率的影响较显著。

3) 与钢轨焊缝不平顺相比，车轮扁疤对轮轨相互作用力的影响更大，因此在有轨电车车辆的日常养护维修过程中应及时对车轮扁疤进行维修。

4) 综合考虑动力学分析结果和实际工况，建议现代有轨电车无砟轨道的设计轮载和常用轮载分别取为静轮载的1.45倍和1.25倍。

需要说明的是，设计轮载和常用轮载的取值受车辆、轨道和线路的参数影响较大，故在确定设计轮载和常用轮载的具体取值时，需要考虑不同有轨电车车辆、无砟轨道类型和线路条件。本文的主要结论和计算方法可为今后有轨电车无砟轨道结构的设计和相应规范的制定提供一定的理论指导。

[1] 曹克非, 陈世浩, 曹宏宇. 亚的斯亚贝巴现代有轨电车适应性研究[J]. 铁道工程学报, 2015, 32(12): 97−102. CAO Kefei, CHEN Shihao, CAO Hongyu. Adaptability research on Addis Ababa tramcars[J]. Journal of Railway Engineering Society, 2015, 32(12): 97−102.

[2] LING L, HAN J, XIAO X, et al. Dynamic behavior of an embedded rail track coupled with a tram vehicle[J]. Journal of Vibration & Control, 2017, 23(14): 2355− 2372.

[3] 翟婉明. 车辆−轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. ZHAI Wanming. Vehicle-track coupled dynamics theory and application[M]. 4th Edition. Beijing: Science Press, 2015.

[4] 蔡成标, 朱胜阳, 刘秀波, 等. 高速铁路无砟轨道疲劳检算轮载的动力学分析[J]. 中国科学: 技术科学, 2014, 44(7): 707−713. CAI Chengbiao, ZHU Shengyang, LIU Xiubo, et al. Dynamic analysis of fatigue check load for ballastless track in high-speed railway[J]. Scientia Sinica Technologica, 2014, 44(7): 707−713.

[5] LEI X, ZHANG B. Analyses of dynamic behavior of track transition with finite elements[J]. Journal of Vibration and Control, 2011, 17(11): 1733−1747.

[6] FENGQ, SUNK, CHENH, et al. Lifetime performance assessment of railway ballastless track systems affected by a mortar interface defect[J]. Journal of Aerospace Engineering, 2019, 32(4): 04019037.

[7] GUO Y, ZHAI W. Long-term prediction of track geometry degradation in high-speed vehicle-ballastless track system due to differential subgrade settlement[J]. Soil Dynamics and Earthquake Engineering, 2018, 113: 1−11.

[8] 李斌, 刘学毅. 基于随机振动理论的我国中高速铁路有砟轨道设计轮载研究[J]. 铁道学报, 2010, 32(5): 114−118.LI Bin, LIU Xueyi. Study on designed dynamic wheel loads of middle-speed and high-speed railways in China based on theory of random vibration[J]. Journal of the China Railway Society, 2010, 32(5): 114−118.

[9] 蔡成标, 徐鹏. 高速铁路无砟轨道关键设计参数动力学研究[J]. 西南交通大学学报, 2010, 45(4): 493−497.CAI Chengbiao, XU Peng. Dynamic analysis of key design parameters for ballastless track of high-speed railway[J]. Journal of Southwest Jiatotong University, 2010, 45(4): 493−497.

[10] 杨荣山, 刘克飞, 任娟娟, 等. 砂浆伤损对轮轨系统动力特性的影响研究[J]. 铁道学报, 2014, 36(7): 79−84.YANG Rongshan, LIU Kefei, REN Juanjuan, et al. Research on effect of cement asphalt mortar damages on dynamic characteristics of wheel-rail system[J]. Journal of the China Railway Society, 2014, 36(7): 79−84.

[11] 高亮, 王璞, 蔡小培, 等. 基于多车精细建模的曲线地段重载列车−轨道系统动力性能研究[J]. 振动与冲击, 2014, 33(22): 1−6, 12. GAO Liang, WANG Pu, CAI Xiaopei, et al. Dynamic characteristics of train-track system in curved track sections based on elaborate multi-vehicle model[J]. Journal of Vibration and Shock, 2014, 33(22): 1−6, 12.

[12] 邓永权, 凌亮, 肖新标, 等. 嵌入式轨道钢轨焊接不平顺安全限值研究[J]. 城市轨道交通研究, 2016, 19(5): 30−34.DENG Yongquan, LING Liang, XIAO Xinbiao, et al. On the safety criterion of welding irregularities on the embedded rail track[J]. Urban Mass Transit, 2016, 19(5): 30−34.

[13] GUO Y, ZHAI W, SUN Y, et al. Mechanical characteristics of modern tramcar–embedded track system due to differential subgrade settlement[J]. Australian Journal of Structural Engineering, 2017, 18(4): 1−12.

[14] John O Hallquist. LS-DYNA Theory Manual[EB]. Livemore: Livemore Software Technology Corporation, 2006.

[15] 刘学毅. 客运专线无砟轨道设计理论与方法[M]. 成都: 西南交通大学出版社, 2010. LIU Xueyi. Design theory and method of ballastless track for passenger dedicated line[M]. Chengdu: Southwest Jiaotong University Press, 2010.

[16] DING J, LIN J, WANG G, et al. Time-frequency analysis of wheel-rail shock in the presence of wheel flat[J]. Journal of Traffic and Transportation Engineering (English Edition), 2014, 1(6): 457−466.

[17] 高建敏, 翟婉明. 高速铁路钢轨焊接区不平顺的动力效应及其安全限值研究[J]. 中国科学(技术科学), 2014, 44(7): 697−706. GAO Jianmin, ZHAI Wanming. Dynamic effect and safety limits of rail weld irregularity on high-speed railways[J]. Scientia Sinica Technologica, 2014, 44(7): 697−706.

Research on the train load value of ballastless track of modern tram

SUN Kui, FENG Qingsong

(Engineering Research Center of Railway Environmental Vibration and Noise, Ministry of Education,East China Jiaotong University, Nanchang 330013, China)

In order to determine the specific values of the design wheel load and the common wheel load of the modern tram ballastless track, according to the principle of wheel-rail interaction, the tarm-ballastless track vertical coupling dynamic model was established. The effects of wheel flat and the irregularity spectrum of grade five lines in the United States on the vertical wheel-rail force under different driving speeds were analyzed in detail. And the difference of wheel-rail force caused by concave and convex rail welding irregularity was compared. Then the statistical analysis of the wheel-rail vertical force data was carried out, and the values of the design wheel load and the common wheel load were obtained. The results show that the wheel-rail vertical force and dynamic load coefficient tend to increase first and then decrease with the increase of driving speed under the excitation of the wheel flat. Secondly, the concave rail welding irregularity has a greater influence on the wheel-rail vertical force, and the convex rail welding irregularity is more significant for the wheel unloading rate. Thirdly, compared with the rail welding irregularity, the wheel flat has a greater influence on the wheel-rail force. Therefore, the wheel flat should be repaired in time during the routine maintenance and repair of the tram vehicle.Finally, it is suggested that the design wheel load and the common wheel load of the modern tram ballastless track are taken as 1.45 times and 1.25 times of the static wheel load respectively.

modern tram; ballastless track; design wheel load; common wheel load; statistical analysis