有序 有道 有度——中考数学复习模拟训练阶段的教学分析与构想

□付 英 廖帝学

（1.重庆市第八中学校，重庆 400033；2.重庆市大渡口区教师进修学院，重庆 400084）

一、中考数学复习模拟训练阶段的三种倾向

综观各地的教学情况，从时间进程来看，很多教师的中考数学复习教学大致可以分为三个阶段：基础复习阶段、专题复习阶段、模拟训练阶段.当然，在每个阶段里完成的教学任务不一定有清晰的界限，通常会在完成该阶段主要任务的同时会兼顾其他.比如，在基础复习阶段，同时也可能会涉及专题复习、模拟训练.

在基础复习阶段，教师会对初中数学各板块知识进行全面梳理，引导学生构建起整体知识结构体系.在专题复习阶段，教师会从数学思想方法总结的角度设计一些专题进行教学，借以提升学生的解题能力和学科素养.在这两个阶段的教学中，教师和学生无疑都是十分紧张和忙碌的.接下来，就是模拟训练阶段了.模拟训练阶段的时间短则一两周，长则三四周.由于经历前面两个阶段的“紧张”和“忙碌”，尽管离中考还有一段时间，但是，一些教师产生了“船到码头车到站”的念头.常见的说法有：

到这个阶段，学生的成绩已经定型，成绩差的不可能再提升，成绩好的也不大可能变差；

这个阶段的主要任务就是心理调适，不必再讲新的内容，适当练一练，适当看一看，只要学生“在状态”就行；

这个阶段，完全看学生自己的“造化”，教师帮不了什么忙……

正是因为有了这些想法，我们看到在这个阶段的教学中有下面几种值得注意的倾向.

倾向一：无序地练

按照中考的要求，教师让学生进行模拟训练，这可以让学生熟悉考试流程，熟悉考试题型，积累应考经验，减缓对考试的紧张情绪.但是，在实际教学中，一些教师在这个阶段的“练”处于无序状态，具体表现有两方面.一是对每次模拟训练的考查目的不明确.每一次模拟训练中都按中考试题的模式进行练习，每一次练习的题目都差不多.这样导致的结果是练得不全面，也助长了学生盲目地猜押考题的风气.二是在这个有限时间段里，对模拟训练的次数比较随意.临近中考，一些教师也随之产生担心，害怕学生“没练到”或“练少了”，随意增加模拟训练次数，加重学生的学习负担.

倾向二：自由地看

一些教师认为，中考复习已近尾声，每个学生的学习情况各有不同，这个阶段应该把时间还给学生，让学生自主地查漏补缺.他们采取的方式是在课堂上让学生结合自己的情况查漏补缺，可以看自己做过的练习本、错题本，可以看教材、查教辅……有问题可以问教师.这种方式，表面上尊重学生的个体学习差异，让学生自主地进行复习.实际上，从数学学科的学习特点来看，这种让学生“自由地看”的方式效果很不好.面对中考，面对三年学的课程，每个学生都不会认为自己每一块内容都百分百没有问题了.每一块都可能有“漏”有“缺”，什么才叫“漏”？什么才叫“缺”？学生不容易想清楚.在这种情况下，让学生“自由地看”，就变得有些漫无目的，浪费时间.

倾向三：重复地讲

在模拟训练阶段，教师难免对训练的情况进行讲评.一些教师讲评的理由和出发点是：“这类问题，我在新课教学时讲过，在基础复习阶段讲过，在专题训练阶段也讲过，学生怎么还会错呢？”接下来的情形就是，教师又针对一个他曾经讲过几次的问题重复了一遍.越到后期，我们越会发现，学生出现的问题大都还是我们平时遇到过的问题.这个阶段的“讲”，稍不注意，就会变成“重复讲”，让学生不敢不听，听了又发现和以前讲的差不多，耽搁了学生的时间.

二、中考数学复习模拟训练阶段的教学构想

（一）有序——模拟训练的“规划”

中考复习的每一个阶段承载着不同的功能，如果把中考复习比作一次跑步的话，“基础复习阶段”相当于“热身起跑阶段”，“专题训练阶段”相当于“加速追赶阶段”，而“模拟训练阶段”则应该是到达终点前的“奋力冲刺阶段”.这种描述，既是针对学生说的，也是针对教师说的.每一个阶段都是“教”和“学”的统一.“行百里，半九十”，如果我们认为最后阶段大都是学生的事，都让学生自己“练”“看”，这样的中考复习不会达到理想效果.所以，对这个阶段的教学，学校、教研组、教师要以模拟训练为主线，整体“有序”地推进.

1.合理规划模拟训练阶段的时间表和路线图

模拟训练的次数不宜过多.每一次训练都应该是在学生有充足的准备之后才进行.模拟训练的主要功能有综合训练、模拟中考、查漏补缺、心理调适等功能.对每一次训练要达到的目的要有准确定位，然后在这个定位下再确定试题的选用.总之，模拟考试是要让学生看到自己的进步，要考出学生的“士气”.

2.教研组要精心研究和命制模拟训练阶段试题

在经历基础复习和专题复习后，教研组可以组织教师结合复习进程再次分析历年中考试题的风格、命题趋势以及在区域内有影响力的一些学校命制的模拟试题，然后再集体确定每一次模拟考试的命题方向.这样可以让教师在这个阶段的“教”和学生在这个阶段的“学”有方向.

在试题命制时，虽然不可能做到完全原创，但一些关键性的题目尽可能地选或编一些利于后期教学的试题.比如，在各地的中考试题中，都有一些“填空题压轴题”“选择题压轴题”，这些题目是很多学生解题的拦路虎.命题者可以通过一些改编题引导学生去尝试逐步解决类似题.

例 1如图 1，在正方形ABCD中，AB=12，点E在边CD上，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长OF交CD于点G，若AB=3EF，则FG的长度是____．

图1

此题是摘取2016 年重庆中考B 卷试题中的填空压轴题的一部分而改编的试题.图形线条减少，计算的步骤减少，让更多的学生能完成.同时，又为教师的评讲作铺垫，连接BF、BG就成为与中考题接近的试题.

例2如图2，菱形ABCD的边长为4，∠A=60° ，E是AD的中点，F是AB边上的一个动点，EG=EF，且 ∠GEF=60° ，则GB+GC的最小值为____．

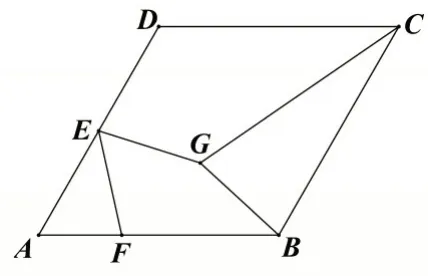
图2

此题中，当点F在AB上运动时，由旋转的知识可知点G也将在一条线段上运动.求GB+GC的最小值就变成学生熟悉的“将军饮马”问题.这样的题目可以让学生知悉试题的命制方式，减少对压轴题的神秘感和恐惧感.

总之，对这个阶段要做什么、怎么做，在思想上和行动上都要有整体架构，思想统一，复习迎考这件事才会变得“有序”.

（二）有道——模拟训练的“讲练”

在模拟训练阶段，教学工作的重点必然是以训练为主.但是，因为有既定的几次模拟考试，教师的“教”和“学”很容易局限于这几套试卷或者被这些试卷牵着鼻子走.一不注意，教师的“讲”“导”的作用就会被削弱.所以，这个阶段，教师要特别注重讲练的“道”，追求讲练的“艺术性”.

1.评讲“全卷”，引导学生经历和体验

精心打磨后的模拟考试的试卷与中考试题有一定的相似度，所以在评讲试卷时，教师常常会引导学生去“理解试卷”，比如让学生体会命题的意图，了解知识点的分布、试题的来源、难度、得分情况、解答的时间安排和先后顺序、全卷的评分标准、书面表达……

学生有前阶段的复习，知识和能力已经有一定程度的积累，这个时候的“经历”和“体验”，可以唤醒学生曾经的“经历”和“体验”，是对学生知识和技能的又一次提升.对解答时间安排和先后顺序、书面表达等的体验，则是从“如何考试”的角度对学生进行指导.

要评讲好“全卷”，教师应有相当丰富的积累，对近年与中考相关的试题应该相当熟悉.特别重要的是，在评讲前，最好能从头到尾将试卷做一遍，评讲时可以与学生分享自己的解题心得，达到与学生“共情”的效果.

2.评讲“错误”，驱动学生整理和反思

在对模拟训练的试题进行批阅后，教师对学生的错误情况已经比较清楚.教师结合这些错误，深入分析产生错误的原因，引导学生由此及彼，整理错误，反思错误.

例3从这六个数中，随机抽取一个数，记为a，若数a使关于x的不等式组至少有三个整数解，且关于y的分式方程有正整数解，求这六个数中所有满足条件的a的值之积是____．

此题涉及含参不等式组和含参分式方程，在对它们的解的情况进行分析时稍稍不慎就不能得出正确答案.在评讲此题时，教师可以多用一些时间对此题的错误进行归类，比如知识性错误、逻辑性错误、策略性错误、心理性错误.由此形成这类题目的解题策略.

3.讲“难点”，促进学生归纳和提升

对模拟训练中的难点问题，教师不能就题论题，“只见树木，不见森林”.重要的是，教师引领学生从某一个难点出发，去归纳突破难点的方法，提升解题能力.

比如，在评讲涉及全等三角形在几何证明中的应用时，教师以北京中考题为例，将2015年～2018 年北京中考几何证明题的图形进行分析，如表1.这样，学生能够结合实例看到全等三角形的各种模型，对试题的理解更深刻，也积累了解题经验.

例 4如图 3，在△ABM中，∠ABM=45°，AM⊥BC，垂足为M.点C是BM延长线上一点，连接AC.（1）略；（2）如图4，点D是线段AM上一点，MD=MC，点E是△ABC外一点，且EC=AC，连接ED并延长交BC于点F，若点F是线段BC的中点.求证：∠BDF=∠CEF．

图3

图4

几何证明一直是学生学习的“痛点”“难点”.此题是以△BMD和△AMC这两个全等三角形为背景命制的试题.问（2）是“求证∠BDF=∠CEF”，证明的方法有很多.教师可以围绕“中点的作用”“辅助线中位线的作用”等信息进行挖掘，让学生经历“证明两个角相等”的多种情形，获得解题体验.

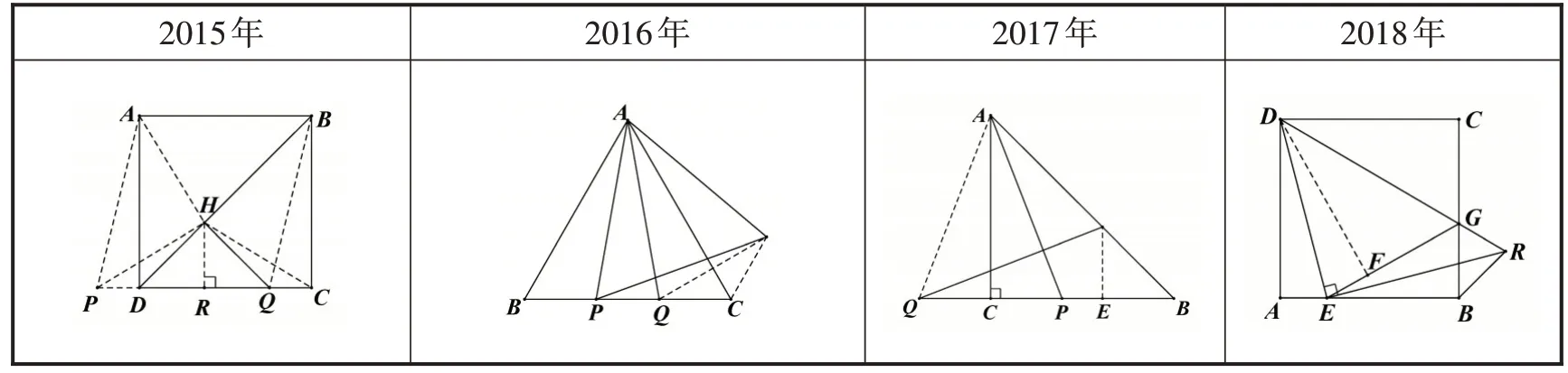
表1

（三）有度——模拟训练的“取舍”

仍然不要放弃每一个学生，仍然要关注试卷上的每一个知识点，仍然既要讲又要练……似乎模拟训练阶段的教学仍然是“面面俱到”，没有什么重点.所以，在这个阶段，我们更要思考教学的“度”，灵活取舍.

1.教师“牵引”有度，让学生自主体验

中考复习的最后阶段，时间紧，任务重.见到学生不会做、出了错教师就着急，一着急就开始“说教”.所以，还是多让学生练习，多让学生量力而行，自己“悟”，自己体验，形成个性化的学习经验.

2.教师“给予”有度，让学生自主获取

由于中考数学的高利害性，社会对中考数学的关注一直处于过度状态.有关中考数学的信息、资源不断地产生.教师对它进行了解、分析，是应该的.在“给予”学生时，要考虑方式和数量，不能增加学生的认知负荷，最好让学生自主获取.

3.教师“激励”有度，让学生自主调适

中考很重要，考高分很好，但是，总是以“中考的重要性”和“高分的优越性”来激励学生也不妥.越到复习的后期，越应注意“激励”的度.这个阶段的学生，心理的调适很重要.教师要找准学生的期望，多鼓励、关爱学生.