例谈初中数学教学中的“德育渗透”*

□于 彬

（东营市胜利第六中学，山东东营 257000）

近日，在一次市级青年骨干教师优质课评选活动中，笔者有幸执教鲁教版“7.1两条直线的位置关系（1）”一课，获得听课教师和评委的一致好评，并获得大赛一等奖的优异成绩.下面对教学设计以及在“德育渗透”方面所做的尝试进行简单介绍，并给出几点思考，不当之处，敬请指正.

“7.1 两条直线的位置关系（1）”选自鲁教版六年级下册第七章第一节第一课时，作为章起始课，本课的教学内容主要包括相交线和平行线的概念、对顶角、互余（互补）的概念及其性质等，是在前面学习了线段、角、多边形等简单基本几何图形的基础上，对相关几何对象的进一步认识和学习.同时，本节课也为后续垂直、平行线的判定和性质的学习奠定了坚实的基础，在教材中起着承前启后的重要作用.本节课力图在使学生掌握必要的“鱼”（知识）、“渔”（技能）、“欲”（兴趣）的基础上，能够在学科育人方面——“育”（德育）进行有益的尝试，进而使学生成为“完整的人”.

一、教学设计简述及德育渗透点说明

（一）创设情境 疑点反思

播放《人民日报》客户端介绍“港珠澳大桥”的一段视频，引导学生在感受其雄伟壮观的同时，从实际物体中抽象出两条直线相交和平行的形象，进而引入课题，并出示学习目标.

追问1：教室和校园里还有相交和平行形象的实物吗？请举例说明.

追问2：这两幅图片（图1和图2）中的直线有什么不同？你能分别给相交和平行下个定义吗？

图1

图2

【德育渗透点说明】以视频的形式引入新课，意在调动学生学习的积极性和主动性，引导学生初次抽象现实世界中相交和平行的形象；同时对学生进行爱国主义教育，以达到学科育人的目的.此外，追问1 继续引导学生观察熟悉的现实世界，对相交线和平行线进行再次抽象；追问2 则直抵问题的本质，促使学生用自己的语言归纳、概括出相交线和平行线的定义.

（二）尝试解疑 问题反思

将图2 中相交线形成的四个夹角分别记为∠1、∠2、∠3和∠4（如图3），它们两两之间有什么关系？（提示：可从数量关系和位置关系两个角度进行回答）

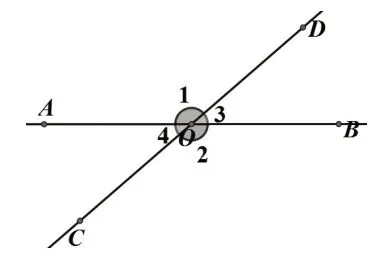
图3

预设1（先发现数量关系）：学生最先发现∠1＋∠3＝180°，∠2＋∠3＝180°，进而得出∠1＝∠2.然后追问：图3 中还有具有这样数量关系（和为180°或相等）的角吗？它们在位置上有什么不同？在此基础上，引导学生对角进行分类，接着得出（邻）补角、对顶角、互补的概念，最后引导学生在理解、类比互补概念的基础上得出互余的概念.

预设2（先发现位置关系，这种可能性较小）：学生也可能说出它们都有公共的顶点，有的有一条公共的边，另一边互为反向延长线；有的两边都互为反向延长线.在此基础上，教师引导学生进行分类，做到不重不漏，得出（邻）补角和对顶角的概念.最后再研究它们两两之间的数量关系，进而得出对顶角的性质以及互补的概念，然后再得出互余的概念.

【德育渗透点说明】上述设计的着力点意在培养学生对几何图形研究的基本方法，即从位置和数量两个方面入手来研究几何图形，为后续学习其他几何图形打下坚实的基础.这样的设计对初学几何的六年级学生来说可能会有难度，但是一线教师应该坚持，用开放性的设问，直抵几何学习本质的思考方式，让学生核心素养的培育成为现实.同时，这样的设计在培养学生严谨的思维（比如条理分明、严谨细致等）和理性的精神（比如勇于探索、善于思考等）方面进行了努力，达到了预期的效果.

（三）牛刀小试 应用反思

牛刀小试1：下列各图中（如图4），∠1 和∠2是对顶角吗？为什么？

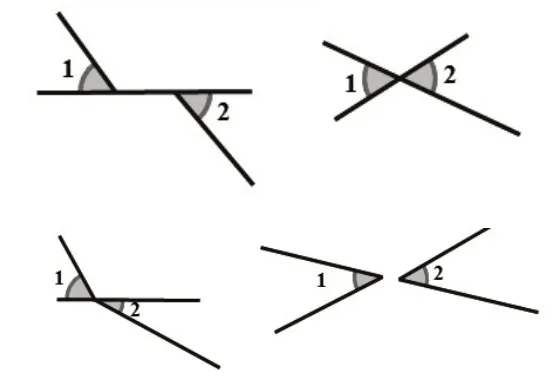
图4

牛刀小试2：下列各图中（如图5），∠1 和∠2互为余角吗？为什么？

图5

【德育渗透点说明】通过上述两个牛刀小试，进一步加深学生对对顶角、互余（补）概念的认识.互余（补）关注的是两个角之间的数量关系，而对顶角则是位置关系决定了数量关系，在掌握相关知识的同时，引导学生从“位置和数量”两个角度去审视对顶角、互余（补）等概念，进而体会数学美，感受真善美.

（四）变式训练 方法反思

图6

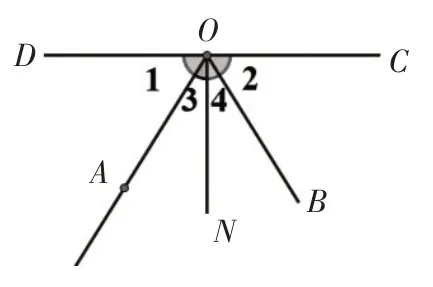
图7

将图6（一个现实生活中的实际问题——台球游戏）简化为图7，ON与CD相交所成的∠DON和∠CON都等于90°，且∠1＝∠2.

问题1：有哪些角互为余角？∠3 和∠4 有什么关系？为什么？

问题2：有哪些角互为补角？∠AOC和∠BOD有什么关系？为什么？

【德育渗透点说明】设计问题1和问题2的主要目的是引导学生在互余和互补概念的基础上分别得出互余和互补的性质.其中问题1在独立思考的基础上，进行小组合作，辅以教师讲解，进而将问题解决；问题2 则是在类比问题1 的解决方法前提下，学生先自行思考，然后辅以学生到黑板上讲解的方式解决，为培养“学会学习和勤于反思”的学生进行有益的探索和尝试.最后，此处还可以进一步培养学生思维的严密性（互余和互补的角能否找全？）和语言表达的准确性（学生如何用自己的语言概括归纳互余或互补的性质？），是进行德育渗透的良好载体.

（五）问题解决 总结反思

问题解决（课堂检测）部分限于篇幅，略.

总结反思环节见图8.

图8

【德育渗透点说明】在师生互动和生生互动中进一步完善板书，指出：我们用数学的眼光观察世界，发现了生活中平行和相交的现象，并抽象出了相交的几何图形；其次，我们用数学的思维分析世界，得出了它们的定义；接着，我们用数学的语言表达世界，得到了它们的性质；最后，我们用所学的知识解决了现实生活中的一些实际问题.

二、对数学教学中“德育渗透”的再思考

笔者认为，“选准‘德育渗透’的切入点、培育‘德育渗透’的延伸线、设计‘德育渗透’的拓展面”都是“德育渗透”的载体，下面给出进一步的思考.

（一）选好“德育渗透”的载体——“鱼”

“德育渗透”最好的载体就是相应的学科知识，即“鱼”.上述课例的“德育渗透”的切入点是借助“港珠澳大桥”中给人以平行和相交形象的实物，得出相交线和平行线的概念这一教学环节；延伸线则是在抽象出两条直线相交的基本图形后开展的对顶角的定义和性质、互补和互余概念的学习；拓展面则是在台球游戏的基础上，再次抽象出几何图形，进而探究互补和互余的性质.以上“德育渗透”点、线、面的设计与实施在对学生进行爱国主义教育、培育理性精神、培养严谨思维以及数学审美观等方面进行了很好的尝试，值得其他一线教师积极践行.

（二）瞄准“德育渗透”的途径——“渔”和“欲”

“德育渗透”的途径则是培养学生对应的学科技能和激发学生对本学科学习的兴趣和欲望.比如该课例中的视频“港珠澳大桥”和动态呈现“白球击打红球，红球进入袋内”的过程，都是在为调动学生学习的积极性和主动性进行尝试，进而增强学生学习的兴趣和欲望——“欲”；此外，教学中用类比相交线的概念得出平行线的概念，以及类比互余研究互补，这些都为学生掌握相关学习方法和研究思路奠定了一定的基础，只有这样才能够在学生的心灵中种下几何学习“基本套路”这粒种子——“渔”，进而倾心浇灌，静待花开.

（三）指向“德育渗透”的归宿——“育”

“德育渗透”的最终归宿则是实现学科育人的目的，为立德树人、培养“完整的人”做出应有的贡献.

上述课例的“总结反思”环节应该是直指“德育渗透”的归宿，即学科育人.在进一步构建知识网络体系的过程中引导学生回忆本节课所学习的知识和解决问题过程中使用的数学思想方法，特别是最后将本节课和数学学科核心素养的“三会”进行深度融合，达到了本节课“德育渗透”的高潮，此乃“点睛之笔”.

我们为此所做的尝试未必准确，更不一定正确，欢迎更多的一线教师参与进来，开发出更多的“德育渗透”的教学案例，为实现“学科育人”的目的贡献一份自己的力量.