基于GBDT的标记分布学习算法研究

2020-06-08王远志陆文成田文泉

安庆师范大学学报(自然科学版) 2020年2期

王远志，陆文成，田文泉，高标

（安庆师范大学计算机与信息学院，安徽安庆246133）

标记是对样本的描述与反映，传统标记学习一般分为单标记学习和多标记学习，单标记学习是假定数据集中的每个样本对应一个标记的学习范式，而多标记学习是将样本对应多个标记的学习范式，且每个相关标记对于整个样本是同等重要的[1]。多标记学习可以更好地处理标记域地不确定问题，能够知道哪些标记描述样本，却不清楚这些标记如何描述样本。但在实际问题中，需要更细致地了解标记对样本的描述程度，而标记分布学习（LDL）则可以很好地处理这类需要了解标记分布强度的问题。Geng[2]等提出了标记分布思想概念，并设计了IIS-LDL算法并应用在自动年龄的估计上，获取到更多的样本信息，从而降低了由于年龄训练数据稀缺带来的风险。后来Geng等[3]规范化定义标记分布学习，设计相关算法，提出衡量算法效果的指标，建立了一套完整的标记分布学习框架。随着不断的研究与发展，标记分布学习在机器学习领域运用越来越广泛[4]，对相关算法预测标记分布的准确度要求也越来越高，因此需要设计出预测结果更加理想的算法。

决策树（Decision Tree）是很常用的机器学习方法，单个决策树处理问题十分有限，通常采用集成学习的思想组合多算法或多分类器得出更理想的结果[5]。在以往研究中，决策树算法能够有效解决多标记学习的问题，如多标记模糊粗糙决策树和基于标记相关特征的多标记决策树算法[6]，通过改进Adaboost处理多标记数据的Adaboost.MH与Adaboost.MR算法[7]等。GBDT（Gradient Boost Decision Tree）是一种迭代的决策树算法，能灵活处理各种类型的数据，适用于大多数回归或分类问题，广泛应用在科研和工业领域[8]。由于标记分布的数据集样本特征较少，需要进行特征变换，相对于其他算法，GBDT能够选择出具有代表性的特征，避免无效特征的干扰，防止过拟化，是非常高效实用的算法。

因此，本文结合GBDT的特性，提出一种基于GBDT的标记分布学习算法GBDT-LDL。该算法是将现有样本特征进行变换组合，生成新的组合特征以提高标记分布的准确程度。在实验部分，采用PTBayes算法、AA-kNN算法、AA-BP算法和SA-IIS算法[9]与该算法做对比，实验结果表明GBDT-LDL比其他算法更具优越性。

1 标记分布学习

1.1 标记分布学习理论

令x表示标记样本，y表示能够代表x的标记，则定义dyx表示y描述样本x的重要程度，该数值取值范围是0到1，且越大越能代表样本。所有标记的描述度构成一种类似概率分布的数据结构称为标记分布，标注样本学习的过程称为标记分布学习[10]。作为一种新的学习范式，在一定条件下，单标记和多标记都可看作标记分布学习的特例，这使得标记分布学习更具泛化性，再运用合适的算法使标记分布学习在实际研究中更具广泛性和实用性。标记学习算法的设计思想可分为3类：问题转换、算法改造和专用算法。问题转换（Problem Transformation）是将标记分布问题转换为传统学习范式处理，典型算法是PTBayes算法。算法改造（Algorithm Adaption）是通过改造某些机器学习算法来适应标记分布学习，典型算法有AA-kNN算法和AA-BP算法。专用算法（Specialized Algorithms）则是设计专门的算法更直接地解决标记分布问题，相关算法有SA-IIS算法。这些算法能有效提高标记分布学习的预测效果。

1.2 评价指标

标记分布学习的预测结果是各个标记的分布形式，类似于数理统计中的概率分布。因此可将衡量两个概率分布之间相似度或距离大小的指标来评价标记分布预测结果的准确度[1]。即将样本的标记分布预测结果和真实数据作比较，通过二者的距离或相似度大小来衡量算法的准确度。其中，二者距离越小或者相似度越大，两个标记分布越接近，结果越好；反之距离越大或者相似度越小，得出的结果越差。本文选用了具有代表性的4个距离标准（Chebyshev距离、Clark距离、Canberra距离和Kullback-Leibler距离）和2个相似度标准（Cosine相似度和Intersection相似度）来作算法的评测指标。

2 结合GBDT的标记分布学习算法

2.1 GBDT算法

GBDT的核心是计算上一轮迭代的负梯度，往减少残差(残差指预测值与真实值的差值)的梯度方向上建立新的决策树，通过不断迭代改进来得到更准确的预测结果[11]。

输入训练集{(x1,y1),(x2,y2),…,(xN,yN)}，损失函数为L(y,f(x))。定义轮数为t=1,2,3,…,T。

对t轮第i个样本计算残差：

对回归树的每个叶子节点计算最小损失函数，得到最佳的叶子节点输出值：

其中Rtj是第t棵决策树对应叶子节点区域，j为树的叶子节点个数，θ为初始常数，则本轮最终的算法模型：

上述是GBDT算法的基本框架，在每轮迭代中，拟合损失函数的负梯度，不断改进从而得出最佳结果，以解决分类或回归问题。

2.2 GBDT-LDL

本文提出GBDT-LDL算法，其原理是利用已有特征让GBDT模型学习，以GBDT中决策树的每个叶子节点对应新的特征，将特征向量取值为0或1。输入的样本点通过某棵决策树中的一个叶子节点，则该叶子节点赋值为1，而该树其他叶子节点为0[12]。GBDT所有树的叶子节点总和将构成新的特征向量长度，利用此原理对特征进行变换与组合。算法主要过程是对于标记分布数据集，将原始数据集分为训练集和测试集，其中训练集分为训练集1和训练集2，首先将训练集1通过GBDT进行特征学习，然后将训练集1通过特征学习模型进行特征变换，对特征变换之后的特征进行归一化处理，与训练集2合并形成新的样本特征数据集。将新的数据集通过GBDT 进行训练，建立特征变换之后的标记分布GBDTLDL模型，通过对测试样本的预测，可以得出准确的样本标记分布。

3 实验过程与分析

3.1 实验数据描述

本文实验总共采用了12组数据集，其中Yeast的9种数据集都是酿酒酵母的数据集，每组有2 465个酵母菌基因样本，每个样本有24个特征，记录各个时间点的酵母菌基因表达水平为标记分布。s-JAFFE和s-BU_3DFE是有243个特征的人类表情数据集，以6种表情作标记，不同人对照片以6种表情作评分处理，然后以评分结果得出标记分布数据。Movie是7 755部电影的评分数据，1 869个特征，5种电影级别作为标记，以该级别人数占总人数比例得出标记分布。具体数据集如表1所示。

表1 实验数据集

3.2 实验方案及结果分析

本文以Windows 10为实验平台，Matlab 2016a为实验环境。采用表1的12组标记分布数据集通过PT-Bayes、AA-KNN、AA-BP、SA-IIS 和本文的GBDT-LDL 5 种算法及6 项评价指标进行对比，实验结果如表2到表7所示。其中，表2到表5代表实验距离度量，数值越小越好；表6、表7代表实验相似度距离度量，数值越大越好。最好的结果已加粗表示。再利用十折交叉验证来测试算法准确性，将原数据集分为10份，轮流实验，得出5种算法的平均值mean和方差sd，再以6个评测指标利用统计分析对比来检验算法。图2表示5种算法在0.05显著性水平下的Nemenyi检验结果，是按照表2到表7的数据结果以算法平均排名建立坐标轴，每个子图横坐标轴中从左至右算法效果依次降低，其中彩色线条连接表示算法之间没有显著差异。

表2 Chebyshev距离实验结果↓

表3 Clark距离实验结果↓

表4 Canberra距离实验结果↓

续表4

表5 Kullback-Leibler距离实验结果↓

表6 Cosine相似度实验结果↑

表7 Intersection相似度实验结果↑

续表7

每个算法对于其他算法有24种比较结果，由图1可知：

①GBDT-LDL 算法在大部分评价指标上性能较优，在37.5%的统计下与其他算法无显著性差异。其中图1（a）显示，在Chebyshev 距离指标上，GBDT-LDL、AA-KNN 和SA-IIS 三者无显著性差异。图1（b）显示，在Clark距离指标上，GBDT-LDL与AA-KNN相比无显著性差异。图1（c）显示，在Canberra距离指标上，GBDT-LDL 与AA_KNN 相比无显著性差异。图1（d）显示，在Canberra 距离指标上，GBDTLDL 优于算法PT-Bayes。图1（e）显示，在 Kullback-Leibler相似度指标上，GBDT-LDL 与 AA-KNN 相比无显著性差异。图1（f）显示，在Cosine 相似度指标上，GBDT-LDL 与AA-KNN 相比无显著性差异。而GBDT-LDL在62.5%的水平下，在统计上对比其他算法效果更优。

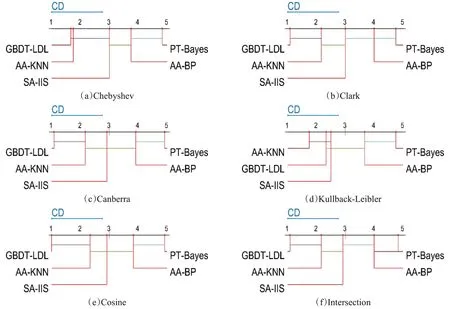
图1 5种标记分布学习算法的Nemenyi检验CD图

②AA-KNN算法在41.7%情况下在统计上优于其他算法，在58.3%情况下与其他算法无显著性差异。

③SA-IIS算法在20.8%情况下在统计上优于其他算法，在79.2%情况下与其他算法无显著性差异。

综上所述，GBDT-LDL 算法性能最优，以62.5%的统计水平优于其他算法，其次AA-KNN 以41.7%情况下优于其他算法，之后SA-IIS以20.8%情况下优于其他算法，最后是AA-BP、PT-Bayes算法。

从不同数据集的数值中相比较可以看出，虽然GBDT-LDL在某些情况下对于其他算法没有显著差异，但整体上按效果由好到差排序是GBDT-LDL、AA-KNN、SA-IIS、AA-BP、PT-Bayes，而GBDT-LDL在各类数据集以及6项指标的实验结果中比其他算法都具有优势，这说明本文算法比其他算法更加能够描述整个标记分布，提高标记分布描述样本的准确性，对标记分布学习在未来实际运用方面更具利用价值。