非线性中立型分数阶微分方程解的存在性

勾明志，付 洋，蔡克珍

（安庆师范大学数理学院，安徽安庆246133）

早在十七世纪七十年代Leibniz就提出了微分方程的概念，其应用非常广泛。分数阶微积分[1-4]的诞生最早可以追溯到创立微积分的时代。它与整数阶微积分是统一的，并且是整数阶微积分的推广，具有遗传与记忆的效应。如今，分数阶作为描述物理及相关学科理论的工具已被接受。分数阶与微分方程二者的结合是有重要意义的，它们的结合便有了更广泛的应用空间。文献[5-8]讨论了下列非线性常微分方程解的存在性

本文对方程（1）进行推广，讨论非线性中立型微分方程解的存在性问题，即

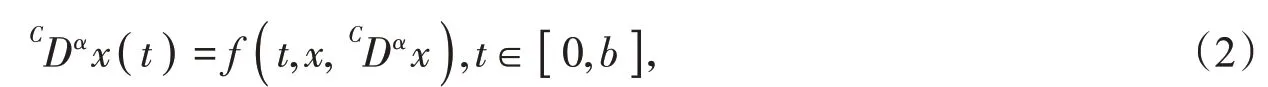
和初值问题x( 0 )=x0，其中，x(t)是在区间[ 0 ,b]上的连续可导函数。当方程（1）利用Lipschitz条件时，只用到一个Lipschitz 常数，即 |f(t,y1)-f(t,y2)|≤k1|y1-y2|,k1∈ ℝ+，而方程（2）要用到具有两个常数的Lipschitz条件 ，即 |f(t,y1,z1)-f(t,y2,z2)|≤k1|y1-y2|+k2|z1-z2|,k1,k2∈ℝ+。当方程（2）用到Picard逐次逼近时，随着逼近的次数越多，分裂的项也就越多，逼近到n次的时候就分裂成了n项。这时再用牛顿二项式定理，将n项进行放大，然后再判别无穷级数的敛散性。与方程（1）不同的是，方程（1）只用到一个常数的Lipschitz条件，无论逼近多少次分裂的项始终是一项。

1 预备知识

下面介绍分数阶微积分中的定义、性质和引理。

定义1[1]设f∈C([ 0 ,+∞ ),ℝ ),t≥ 0,对 ∀α∈ ℝ+，称为f(t)的α阶分数积分，其中Γ(⋅)为Gamma函数。

定义2[2]设f∈C([ 0 ,+∞ ),ℝ ),t≥ 0,∀α∈ (0,1)，称的α阶Caputo型分数导数。

性质1[3]分数阶积分算子满足如下线性关系

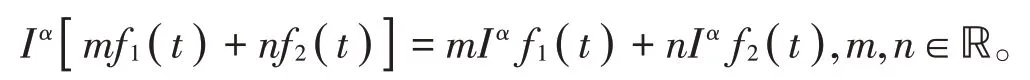
性质2[3]分数阶积分算子满足合成复合运算性质。

引理1[10]对于（2）式和满足初值的积分等价方程为

条件（H） 对于函数f(t,y,z)满足Lipschitz条件可表示为

其中k1,k2称为Lipschitz常数。

2 主要结果

利用Picard逐次逼近法获得满足初值问题的微分方程（2）解的存在性结果。

定理1若满足初值问题的常微分方程（2）满足条件（H），（i）当b≤ 1时，且满足，则方程有解；（ii）当b＞ 1时，且满足时，则方程有解。

证明根据引理构造如下Picard逐次逼近函数列。取，

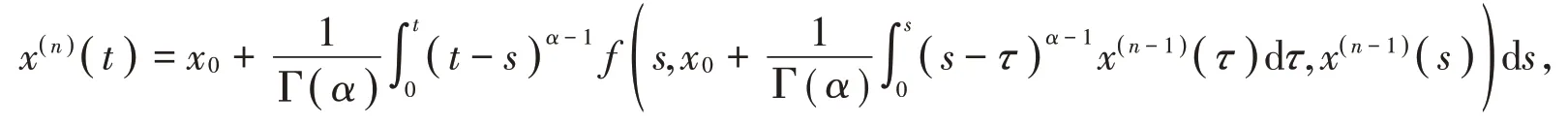
即

为了得到结果，需要考虑函数列x(n)的敛散性，首先，把x(n)作如下分解，

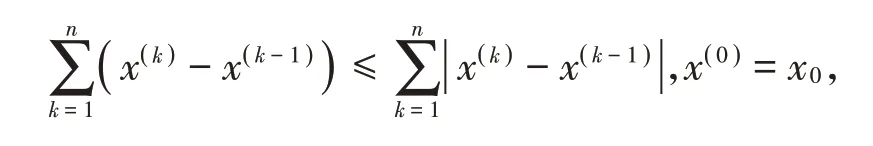
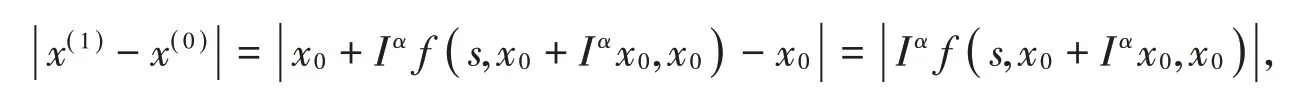
存在正实数M，使得成立，可得

以此类推可得

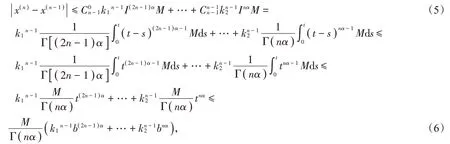
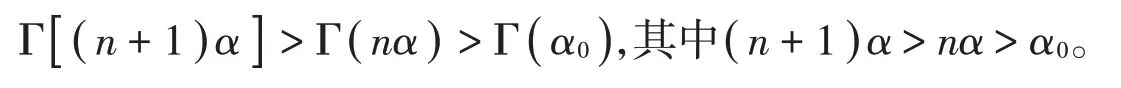
接下来分两种情况讨论。

（i）当b≤ 1 时，由（4）式可得根据 D,Alembert判别法可得：

接下来讨论第二种情况。

（ii）当b＞ 1 时，由（4）式可得根据D,Alembert判别法可得

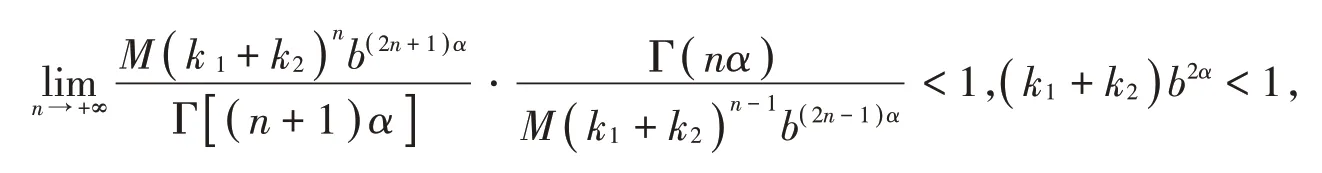
当对（5）式采取不同方法缩放时，得到的结果也不同，接下来的定理是对（5）式采取不同的处理方法得到的结果。

定理2若满足初值条件的方程（2）满足条件（H），且则方程（2）有解。

证明由（5）式，得

其中t∈ [ 0 ,b],n=1,2,…。对于α＞ 0，存在唯一α0∈ (1 ,2 )使得Γ(nα)＞ Γ[(n-1)α]＞ Γ(α0)，其中nα＞ (n-1)α＞α0，可得

用D,Alembert判别法可得

接下来证明解的唯一性。设满足条件（H），φ(t)和φ(t)是方程（2）在t∈ [ 0 ,b]上的两个解。由（3）式可得

根据D,Alembert 判别法可得：当时 ，级 数收 敛 ，即故方程具有唯一解。用同样的方法也可以证明定理1有唯一解。

3 应用举例

下面通过举例来说明定理的适用性。

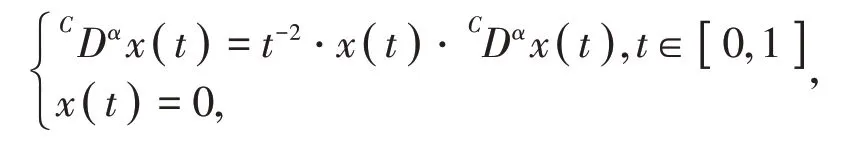
其中x(t)＞0且导数连续。

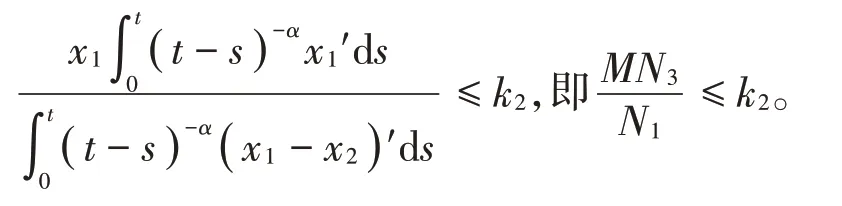
4 总 结

本文巧妙地运用了二项式定理讨论了一类中立型分数阶常微分方程初值问题解的存在性，从而将复杂的公式简便化。文章虽然对一些已有结果进行了推广，但不足之处是此类微分方程并不含有时滞项，所以本文还可以推广到含有时滞的微分方程中去。