一类数字半群容许的型
2020-06-08孙广人
潘 萍,孙广人,吴 琳,凌 燕
(安庆师范大学数理学院,安徽安庆246133)
令ℕ是所有非负整数构成的集合,若ℕ的子集S包含0,对加法封闭,且S在ℕ中补集有限,则称S是数字半群。S中最小的非零整数称为S的重数,用m(S)表示。S的导子是唯一的整数c∈S,使得c-1∉S且c+N∈S[1]。不属于S的最大正整数称为S的Frobenius数,用F(S)表示,F(S)=c-1。令x∉S,若对任意的正整数s∈S,有x+s∈S,则称x是S的伪Frobenius 数,用PF(S)表示。令A是 ℕ 的非空子集,由A⊆ℕ生成的ℕ的幺子半群是最小的包含A的幺子半群,通常用A表示,即
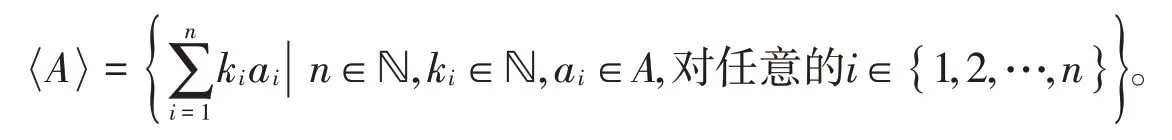
不难证明当且仅当A中元素的最大公约数为1时,A是数字半群[2]。因为当A中元素的最大公约数大于1时,A在ℕ中的补集不是有限的,故在此情况下A不是数字半群。若S是数字半群且A是S的子集,则A是S的生成元系,即A=S。若没有A的其他真子集生成S,则称A是S的极小生成元系,用E(S)表示。每个数字半群都有唯一的极小生成元系,且极小生成元系具有有限多个元素[3],称极小生成元系的基数为S的嵌入维数,用e(S)来表示。
目前数字半群及其理想的型(pattern)是一个研究热点问题[4-9]。文献[4]中引入了数字半群的型的概念,并描述了至少可以被一个数字半群容许的型,并定义为可容许型,还介绍了减法型以及布尔型;文献[5]研究了非齐次线性型被容许的条件;文献[7]介绍了数字半群的理想的型。本文是在此基础上,研究形如的数字半群所容许的型。
文中集合{ 0 ,m,→ }中的“→”表示m后续的所有自然数都属于这个集合表示数字半群S中的非零元素n的 Apéry 集,即{x∈S|x-n∉S};amodb表示a除以b的余数;I-J表示集合对任意的a∈J};nM(S)表示几个M(S)集合相加,即集合。
1 型
长度为n的型p是关于x1,x2,…,xn的具有非零元系数的线性多项式,即若对数字半群S中的任意n元非增序列(x1,x2,…,xn),有p(x1,x2…,xn)∈S,则称数字半群S容许型p(x1,x2…,xn)。当a0=0时,称型p为齐次线性型;a0≠0时,则称型p为非齐次线性型。
命题1给定一个型则下列条件等价:(1)存在一个数字半群容许p,(2)ℕ容许p,(3)对任意n′≤n,有满足这3个条件中的任意一个条件的型称为可容许型。
定义1[4]给定一个型设
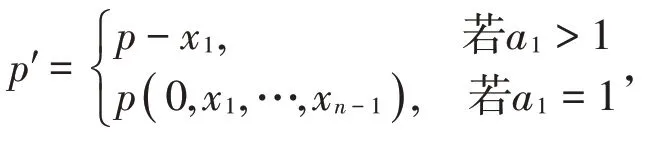
若p是容许型,且p′也是容许型,则称型p是强容许型。
命题2[4]令是长度为n的强容许型,则对任意的x1≥x2≥…≥xn,有p(x1,x2,…,xn)≥x1≥…≥xn。
定义2若除最后一项系数为-1外,其余项系数都为1,则称型p为减法型,且减法度为n-1。
定义3若型的系数全为1或-1,则称型为布尔型。
命题3[4]若型p具有有限正容许度k,则型p为

其中,f中所有系数为正,g,h都是可容许的,且g中所有系数之和为0,h中系数之和非负。
称数字半群{ 0 ,m,→ }为常半群,即半群{ 0 ,m,→ }={ 0 }⋃{z∈ ℕ|z≥m}。令q∈Q,定义是所有整数的集合)。
引理1令m为正整数,则是数字半群。
证明已知显然 0 ∈S。对任意的a,b∈S,满足a+b∈S,因此可得S对加法封闭。又因为{ 0 ,m,→ }是数字半群,{ 0 ,m,→ }⊆S,故S在ℕ中补集有限。因此,S是数字半群。
引理2令m为正整数,则数字半群具有极大嵌入维数。
证明①当m为奇数时,有,
其中

②当m为偶数时,有,
其中

引理3令m为正整数,则数字半群是Arf数字半群。
证明已知故c=m-1。要证明S是Arf数字半群,需证明对任意的x,y,z∈S且x≥y≥z,有x+y-z∈S[10]。
①若x≥m-1,则对任意的x,y,z∈S且x≥y≥z,故y-z≥ 0,因此有x+y-z≥x≥m-1∈S;
②若x<m-1,因为x,y,z∈S且x≥y≥z,所以有。又因为S是数字半群,故S对加法封闭,因此对任意的x,y,z∈S且x≥y≥z,有x+y-z∈S。综上所述,对任意的x,y,z∈S,x≥y≥z,有x+y-z∈S,故S是Arf数字半群。又由文献[7]可知Arf数字半群容许Arf型,因此数字半群容许Arf型。
定理1令m为正整数,则数字半群容许任意的强容许型。
证明令是强容许型。已知由命题2可知,对S中任意的非增序列(x1,x2,…,xn),有p(x1,x2,…,xn)≥x1≥…≥xn。
①若x1≥m-1,则p(x1,x2,…,xn)≥m-1∈S。
②若x1<m-1,则对任意的有因此分3种情况讨论:
(i)当x1=0=x2=…=xn时,有;

综上所述,数字半群S容许任意的强容许型。
定理2令m为正整数,则数字半群容许任意的减法度大于等于2的减法型。
证明令型p(x1,x2,…,xn-1,xn)=x1+x2+…+xn-1-xn是减法度为k的减法型,即

假设k≥ 2,且(x1,x2,…,xk+1)是S的非增序列。要证p(x1,x2,…,xk,xk+1)∈S,则需要分2种情况讨论:

正如假设的k≥ 2,则p(x1,x2,…,xk,xk+1)≥( 2 -1 )(m-1 )=m-1。又由引理2可知F(S)=m-2,因此p(x1,x2,…,xk,xk+1)>F(S),故p(x1,x2,…,xk+1)∈S。
假 设k< 2 ,且 数 字 半 群S容 许 型p。 由x1=m,x2=m-1 可 得p(x1,x2)∈S。 然 而m-(m-1 )=1∉S,这与上述条件矛盾,故S不容许任意的减法度小于2的减法型。
定理3令m为正整数,则数字半群容许任意的可容许度大于等于2的布尔型。
工程高边坡危害后果分析是通过对边坡影响范围内的承灾体进行识别,分析承灾体价值、灾害到达承灾体概率、承灾体时空概率、承灾体易损性,进而估算人身伤害损失和财产损失[15]。
证明令型p是长为n、可容许度为k的布尔型。令f、g、h如命题3所示,f中所有系数为正,g中所有系数之和为0,且h中的系数之和非负,记为X。
假设k≥ 2,且(x1,x2,…,xn)是S的非增序列。要证p(x1,x2,…,xn)∈S,则分2种情况讨论:① 若,则因此可得,其 中b,c∈ℕ 。 于 是 有p(x1,x2,…,xn)=f(x1,x2,…,xk-1)+。
假设k<2且S容许型p。由文献[4]中命题43可知减法度为k的减法型诱导可容许度为k的布尔型,因此S也容许减法度小于2的减法型。然而,由定理2可知S不容许减法度小于2的减法型,这与前面的条件矛盾。故S不容许可容许度小于2的布尔型。即S容许任意的可容许度大于等于2的布尔型。
例1令m=8,有数字半群S={ 0 ,4,7,→ },则S容许型p=x1+x2-x3+x4-x5。
命题4令m为正整数,则数字半群被S容许,则对任意的a0∈S,有S容许型。
例2令m=10,有数字半群S={ 0 ,5,9,→ },则S容许型p=x1+x2-x3+11。但因为有0 ∈p(S),所以只有满足a0>0时,非齐次线性型是可容许型。因此,若要研究a0<0,则需要在S的理想上进行研究。
数字半群S的相对理想是满足对d∈S,有H+S∈H且H+d∈S的集合H,H∈ℤ。S中包含的相对理想是S的理想,若S的理想不同于S,则称这个理想是S的真理想。S的真理想集中的最大元素称为S的极大理想,即S的非零元素集,用M( )S表示[7]。
命题5令m为正整数,则被S的极大理想M(S)容许,则对a0∈PF(S),有S的极大理想M(S)容许型。
定义4[7]令I和J是数字半群S的两个理想。对于d∈ℕ{ 0 },定义集合
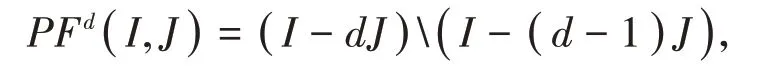
且称PFd(I,J)为从I相对于J的距离为d的元素集。
数字半群S相对于它的真理想J的李普曼半群是L(S,J)= ∪h≥1(hJ-hJ)[10-11],这也称为J的单相交。半群L(S)=L(S,M(S))也称为S的李普曼半群或S的单相交。若存在h0≥1,使得对每一个h≥h0,L(S,J)= (hJ-hJ)或(h+1)J=hJ+m(J)成立,则称h0为J的约化数。
定理4当数字半群S具有极大嵌入维数时,则PFn(S,M(S))=E(S)-nm(S)。
证 明定 义D(d,M(S))={z∈ ℤ|z+dM(S)⊆S,z+dM(S)⊄dM(S) },即D(d,M(S))={z∈ ℤ|z+dM(S)⊆S,z+dM(S)⋂(SdM(S))≠ ∅}。
对n进行归纳假设。当n=1时,结果显然成立。假设n-1时,结果也成立。下面证明当n时结果也成立。
根据定义,若d使得L(S)= (dM(S)-dM(S)),则(S-dM(S))=L(S)⋃D(d,M(S))。当S具有极大嵌入维数时,则对任意h≥1,S的李普曼半群L(S)= (hM(S)-hM(S) )[7]。因为

故有D(n,M(S))D(n-1,M(S))={z∈ ℤ|z+nM(S)⊆S,z+nM(S)⊄nM(S),z+ (n-1)M(S)⊄S},则PFn(S,M(S))= (S-nM(S))(S-(n-1)M(S))=D(n,M(S))D(n-1,M(S))=
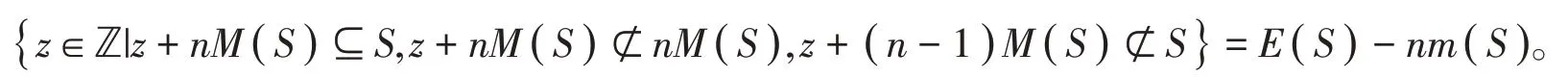
推论令m为正整数,数字半群则对任意

例3令m=9,有S={ 0 ,4,8,→ },则M(S)容许型p=2x1-x2+x3-1。因为-1∈E(S)-3m(S)={-8,-3,-2,-1 }。因此,M(S)也容许p=2x1-x2+x3-8。
4 总 结
目前数字半群理论与交换代数、组合学、图论、代数几何以及编码理论等领域联系紧密,而对于数字半群上的型的研究可用于探索容许它们的数字半群的性质。本文针对文献中引入的数字半群上的型的概念以及数字半群容许型所需要满足的条件,将研究对象推广到具体的数字半群S=上,探究其容许的齐次线性型和非齐次线性型。
