冰晶颗粒的浮升融化过程
2020-06-08张雨龙
张雨龙,张 鹏,马 非
(上海交通大学 制冷与低温工程研究所, 上海 200240)
随着经济和社会的发展,能源消耗量越来越大,由此导致的能源紧缺和环境污染等相关问题也日趋严重,能源的高效利用就显得尤为重要.蓄热技术是提高能源利用率最有潜力的技术之一,采用蓄热系统可以高效利用可再生能源和余热资源,通过对能量实现短期或长期的储存以及再释放,能够有效提高能源的利用率[1-3].例如,在制冷领域将蓄冷技术可以应用于二次制冷回路,从而减少制冷剂用量并提高制冷效率[4].使用相变材料的蓄热系统已经广泛地应用于建筑、电力设备、制冷、空调以及食品等行业[5].近年来,相变浆体由于既可以作蓄热介质又可以作换热介质,被广泛地应用于各个领域[6-8].由于相变浆体是固液两相流体,固相颗粒和液相载流体之间的热质传递对相变浆体的流动与传热有重要的影响和作用.为了更好地利用相变浆体,需要对相变浆体中固相颗粒和液相载流体之间的热质传递机理有更深入的认识.冰浆因具有良好的流动性以及较高的潜热而在蓄冷和载冷方面有较大的优势.
目前对固相颗粒在流体中的运动相变过程的研究主要集中在数值计算方面.刘汉涛等[9]使用了任意Lagrange-Euler(ALE)算法对椭圆颗粒在竖直通道中的沉降过程进行了模拟,结果表明流体的对流、颗粒的质量以及形状的变化对颗粒在沉降时的尾迹和沉降速度有较大的影响.Shabgard等[10]假定颗粒的形态在融化过程中保持为球形,采用移动网格的方法研究了多个相变颗粒在竖直平行管道内的换热过程.研究表明,在颗粒所占固相体积分数较大的情况下,改变颗粒的初始半径对管道整体的换热性能影响很小.上述数值模型在假定颗粒保持球形融化的条件下能够获得平滑的相界面,有利于研究固液两相间的动量交换和能量交换特性,在处理固液之间相互作用的问题上有一定的优势,但在实际融化过程中固相颗粒的形态很难保持为球形.Gan等[11]在二维情况下用ALE算法对固体颗粒受自然对流换热以及强制对流换热作用下的融化过程进行了直接数值模拟,发现颗粒的融化不仅会改变颗粒的形态而且会直接影响颗粒的运动过程,并获得了沿相界面的局部换热系数分布.研究结果表明,相界面上的局部换热系数有明显差异,各个位置的融化速率也不相同.实际上,在颗粒运动融化过程中,由于固液两相界面上不同位置附近的流场有差异,极易使颗粒的形态发生不规则的变化.
为了更深入地理解颗粒非均匀融化过程中涉及的热质传递过程和机理,本文在文献[12]的基础上建立了冰晶颗粒在水中自由浮升融化过程的数值模型,采用焓-多孔介质法追踪固液界面的移动.考虑固体颗粒内部导热以及初始状态下颗粒内部过冷的影响,对冰晶颗粒浮升融化过程中的温度场、速度场及两相间的热质传递特性和机理进行了研究.
1 模型描述
1.1 物理模型
所建立的物理模型如图1所示.其中:r为径向坐标;z为z向坐标.竖直通道内充满温度为T0的水,直径dp=0.002 m的冰晶颗粒在初始位置(0.0, 0.0) m处自由浮升并受到周围流体的加热而逐渐融化,通道长H=10dp,宽W=20dp.有关参数:水的密度ρf=998.2 kg/m3,热导率λf=0.6 W/(m·K),运动黏度μf=1.001×10-3m2/s;冰晶颗粒的初始温度为Tp,密度ρp=913.0 kg/m3,导热系数λp=2.2 W/(m·K);相变温度Tm=273 K.
计算区域为二维轴对称的矩形区域,重力方向向右.颗粒的密度较小,在浮力作用下进行浮升运动,由于浮升距离过长,在绝对坐标系下的计算区域过大,会消耗大量的计算资源.为了节省计算资源,采用移动坐标系(MRF)法研究颗粒在流体中的运动,以通道为绝对坐标系.在浮升过程中颗粒保持相对静止,通过每一个时间步长求出颗粒在绝对坐标下的浮升速度.在移动坐标系下,流体以相同的速度沿颗粒运动的反方向从入口流入.
1.2 数值模型
在计算中采用如下假设对模型进行简化:① 固相和液相的热物性不同,但是均不随温度发生变化;② 忽略由于流体密度变化引起的自然对流;③ 不考虑微尺度下颗粒的Gibbs-Thomson效应,即颗粒在融化过程中的相变温度恒定为Tm;④ 颗粒雷诺数Re从初始时刻到完全融化的过程中比较小,颗粒的旋转效应可忽略.
焓-多孔介质法的主要思路是采用焓和温度一起作为待求变量,在整个区域(包括液相、固相和两相区域)建立统一的能量方程,利用数值方法求出焓的分布,然后确定两相界面.因此,无需跟踪界面,而是在每一个时间步长通过液相分数来捕捉两相界面.由于颗粒和通道均为轴对称的,模型采用极坐标,其连续性方程为
(1)
式中:vr为径向速度;vz为z方向速度;ρ为密度;t为时间.动量守恒方程为
(2)
能量守恒方程为
(3)

href为基准焓,Tref为基准温度,cp为颗粒比定压热容.另外,ΔH可以认为是与液相分数成正比的量,固相时潜热为0,液相时为Lf,则有
ΔH=βLf
(6)
(7)
式中:Tsol为相变温度下界,取为273 K;Tliq为相变温度上界,取为273.3 K.
对于固相颗粒,其在流体中的运动过程受到多个力的作用,因此需要对其受力和运动进行描述.冰晶颗粒在初始速度为0的状态下浮升,受到重力、浮力、流体的曳力、因加速运动而产生的虚质量力以及Basset力的作用.因此,颗粒运动的动量方程为
(mp+CAρfVp)dvp/dt=
(8)

图2 数值计算结果与文献结果对比Fig.2 Comparison between numerical results and results from the literatures
式中:mp,d,Vp分别为颗粒的质量、直径、体积;CD为无量纲的曳力系数,这里采用文献[13]的经验关系式;t′为积分变量;CA和CH分别为虚质量力常数和Basset力常数[14];g为重力加速度.
针对以上数学模型,计算中所有网格均采用四边形网格,并对颗粒及颗粒周围的网格进行局部加密.根据试算,在网格数量大于4×105时的计算结果随网格密度的变化较小,因此采用的网格数量为5×105.连续性方程、动量方程以及能量方程离散均采用二阶迎风格式,收敛标准分别为10-4、10-5以及10-8,采用SIMPLE算法进行求解.另外,由于采用了移动坐标系进行研究,需考虑坐标系变化对动量守恒的影响,在动量方程中加上了额外的源项(式(2)中z方向动量方程的右端最后一项),且通过测试计算,发现该项对整体计算结果的影响很小,可以忽略.根据能量方程解得的温度可以获得液相分数分布.一般来说,液相分数越接近于1,得到的界面越接近于实际情况.分别在计算中取液相分数区间[0.94,1], [0.95,1], [0.995,1],[0.999 5,1]为两相之间的界面,发现颗粒半径随时间的变化曲线没有明显差异,故取液相分数[0.95,1]的区域为两相之间的界面.由于颗粒的形态可能会发生不规则的变化,以相界面上各点与颗粒中心点距离的平均值作为等效半径R,以便于曳力的计算以及分析颗粒的粒径变化.
2 模型验证
上述数值模型涉及到颗粒在流体中运动和传热两个过程,通过数值结果与实验及经验公式的对比(见图2)来分别验证这两个过程模型的准确性.
2.1 单颗粒在竖直通道中的沉降
针对颗粒在流体中的运动过程,Ten等[15]通过实验研究单颗粒在充满硅油的箱体中沉降的过程,采用粒子图像测速(PIV)法测量获得了不同工况下,颗粒运动速度随时间的变化过程.根据其实验条件计算了单个颗粒在等温流体中由于重力作用的沉降过程,流体与颗粒之间无质量和热量交换.颗粒直径为 0.001 5 m,密度为 1 120 kg/m3,按照文献中的实验条件,当Re=1.5, 4.1, 11.6, 31.9时,颗粒沉降速度随时间变化的曲线,如图2(a)所示.从图2(a)中可以看到,数值结果与Ten等[15]的实验结果有较好的一致性.
2.2 水平通道中颗粒与流体的对流换热
通过计算不考虑传质过程的静止颗粒与稳定来流的对流换热过程来验证颗粒与流体之间的换热.温度为273 K的颗粒固定于水平通道的中心处,温度为283 K的流体以恒定速度流过颗粒并进行换热.在不同的来流速度条件下,可以获得不同Re下的换热努塞尔数Nu,如图2(b)所示.由图2(b)可知,本文结果与文献[16]所给出的经验公式非常吻合.这说明了本文数值模型在分析计算颗粒与流体换热方面具有较好的准确性,能够用于描述冰晶颗粒与流体的换热过程.

表1 不同工况的初始条件Tab.1 Initial conditions for different cases
3 结果与讨论
对于2.1节中所描述的冰晶颗粒浮升融化过程,针对不同温差(流体与颗粒)下的颗粒浮升融化和颗粒内部有过冷条件下的浮升融化进行了对比研究.冰晶颗粒在浮力作用下从初始位置开始浮升运动,与流体之间发生热质交换并逐渐融化.为方便分析,假设颗粒由初始状态融化至颗粒半径为初始半径的5%时所经历的时间为颗粒融化的总时间ttot,定义无量纲时间t*=t/ttot.考虑到当流体与颗粒之间温差过大时,冰晶颗粒的融化时间太短不利于研究颗粒的换热特性和运动状态的变化,故在研究时将流体与颗粒之间的温差定为10 K及13 K.为了研究换热温差及颗粒内部过冷的影响,设计了6组对比工况1~6,具体参数如表1所示,其中Tdos为过冷度.颗粒与流体换热的平均Nu根据下式计算:
(11)
QA=LfΔVρp+cpdTmp
式中:ΔV为前一个时间步长内冰晶颗粒由于融化产生的体积减小量,dT为当前时间步下颗粒的温升.
3.1 冰晶颗粒浮升融化过程分析
冰晶颗粒在浮升过程中受到多个力的作用,其中虚质量力和Basset力是由于颗粒从静止状态突然开始加速运动而产生的,只在颗粒初始的加速阶段对颗粒的运动状态有较大的影响.颗粒从初始状态到融化结束时刻的速度变化曲线如图3所示.在初始阶段,冰晶颗粒由于运动速度小,所受曳力也比较小,而颗粒由于融化较少,体积变化不大,因此颗粒所受浮升力(为方便分析,定义浮升力为重力与浮力的合力)起主要作用,浮升力所产生的加速度较大.随着颗粒浮升速度的增加,颗粒所受曳力逐渐增大,且颗粒所受浮升力由于颗粒的融化而减小,所以颗粒浮升的加速度逐渐减小.当t=0.479 s时,颗粒所受的浮升力与其他力相平衡,颗粒的加速度为0,其浮升速度达到最大值.在此时刻之后,颗粒的浮升速度开始逐渐减小.这是由于此时颗粒的运动速度较大,即所受流体作用的曳力起主要作用,而颗粒由于融化导致体积减小,使得颗粒所受的浮升力小于曳力.因此颗粒虽然仍向上浮升,但加速度方向与运动方向相反,颗粒逐渐减速.随着颗粒的持续融化,浮升速度由于冰晶颗粒的体积越来越小而持续降低,直至冰晶颗粒融化完全,颗粒运动速度减小至0.

图3 冰晶颗粒浮升融化过程中的速度变化曲线Fig.3 Evolution of ice particle velocity during melting and floating process
为了更好地理解颗粒在浮升融化过程中的运动及非均匀融化过程,在工况1条件下,液相场以及温度场分布如图4所示,其中yflo为当前时刻冰晶颗粒向上浮升的距离.取t*=0.015,0.345,0.895时的分布进行对比.相应时刻的速度矢量场分布及其局部放大图如图5所示,其中v*为无量纲速度,v*=v/vp.

图4 工况1下不同时刻的液相场及温度场分布Fig.4 Distribution of liquid phase and temperature at different instants in Case 1
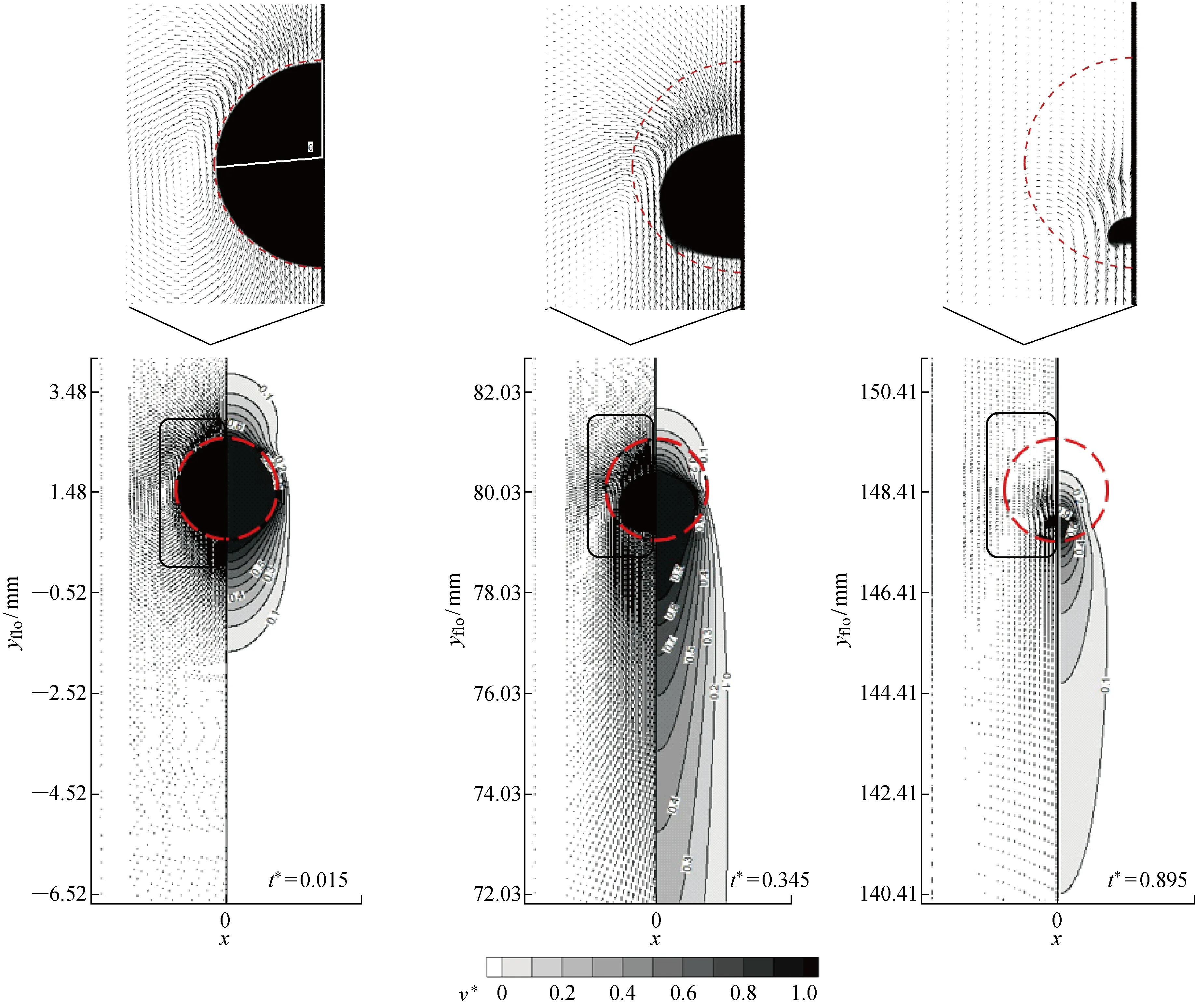
图5 工况1下不同时刻的速度矢量场(左侧)及其局部放大图和速度场(右侧)分布Fig.5 Velocity vector field (leftcolumn) with its local magnification and velocity field (right column) distribution at different instants in Case 1
图4中右半部分为温度场,左半部分为其相应的液相分数场.其中,温度T*为无量纲温度,T*=(T-Tp)/(T0-Tp).为了方便观察,图中用红色虚线表示颗粒初始的轮廓.由液相分数的分布可以看到,颗粒的形状由规则的圆形逐渐向不规则的椭圆形转变,颗粒的尾端越来越平坦,最后变为不规则的类似方形的小颗粒,颗粒呈现出非均匀融化的特性,这是以往研究中假设颗粒保持球形融化所无法得到的.对比红色的虚线颗粒轮廓可以看到在t*=0.345时,冰晶颗粒的顶端由于融化已经向下移动了1/2的距离,而颗粒的尾端只有少许融化,这说明冰晶颗粒顶端融化速率明显快于尾端.
由图5可以看到,冰晶颗粒的顶端流体的速度明显高于尾端,由于冰晶颗粒浮升过程中颗粒与流体之间的换热主要为对流换热作用,颗粒附近区域的流体速度越快,颗粒与流体间的对流换热作用越强,因此颗粒顶端融化的速率相比于底端更快.此外可以看到,冰晶颗粒角度θ=100°时附近有涡旋产生,t*=0.345时颗粒的浮升运动的Re较大,所以涡旋更为明显.从图5所示的速度矢量场放大图中可知,颗粒尾端区域流体的速度要高于θ=100° 时颗粒附近的流体速度,尾部区域冰晶颗粒与流体间的对流换热作用较强.因此,颗粒尾部的融化速率高于颗粒侧面,使得颗粒尾端逐渐变得平坦.从图4中t*=0.895的液相分布可知,颗粒底端从初始的圆弧线变为近似于直线.
3.2 换热温差及内部过冷度对冰晶颗粒浮升融化的影响
从上述分析可以看出,冰晶颗粒的浮升融化过程受到速度场和温度场的耦合作用,其浮升速度与颗粒的体积有关,而颗粒的体积受到融化速率的影响.同时,由于颗粒的非均匀融化,使得颗粒周围流体的速度分布也发生了变化,进而影响换热.对6种不同工况下的计算结果进行分析,以研究换热温差以及内部过冷度对冰晶颗粒浮升非均匀融化过程的影响.由图3可知,不同工况下的颗粒由静止到加速直至浮升速度达到最大值的过程大致相同,且在t=0.479 s左右,而减速过程则出现了明显的差异.这是因为加速过程进行的时间较短,不同工况之间颗粒粒径的变化相差不大,颗粒与流体间的换热对速度的影响较小.而颗粒的减速过程持续时间较长,在此阶段,由于不同工况下换热温差的不同以及初始过冷度的影响,颗粒的尺寸变化会有差异,颗粒尺寸减小的越快,其速度减小的也越快.这是因为减速过程中,相同运动速度下颗粒所受的曳力几乎相同,而颗粒的体积越小则所受的浮升力就越小.不同工况下颗粒等效半径的变化情况如图6(a)所示.由图6(a)可以看到,不同工况下颗粒半径减小的趋势与图3中颗粒浮升速度的减小趋势相对应.另外,与工况1相比,工况2、工况3中颗粒的过冷度逐渐增加,其融化时间也逐渐增加.工况2相比于工况1的颗粒融化时间增加了9.8%左右,工况3相比于工况1的颗粒融化时间增加了14.1%.此外,对比工况4~6,也能观察到上述规律.这说明颗粒内部过冷对于冰晶颗粒的融化有极大的阻碍作用.而相比于工况1,工况4下由于冰晶颗粒与流体之间的换热温差增加了3 K,颗粒融化时间减少了18.3%左右.对比工况5与工况2、工况6与工况3,也能发现类似现象.这说明增大颗粒与流体之间的换热温差可以加速颗粒的融化.
不同工况下冰晶颗粒融化过程Nuave随时间的变化如图6(b)所示.由图6(b)可知,不同工况下颗粒Nuave变化趋势大体相同,都是随着时间的增加先增大然后逐渐减小.这是因为颗粒的Nuave受颗粒运动速度的影响,其变化趋势与图3中颗粒运动速度的变化趋势相同.分别对比工况1~3以及工况4~6,可以发现随着过冷度的增加,颗粒最大Nuave出现的时间发生了延后,且过冷度越大,延后的时间越长.这是因为在计算Nuave时,颗粒获得的总热量包含颗粒升温的显热,流体与颗粒间的换热温差随着颗粒升温而逐渐减小,因此Nuave持续上升,直至过冷度完全消失时Nuave达到最大值.而初始的过冷度越大,过冷度完全消失的时间就越长,造成了颗粒最大Nuave出现的延后时间越长.在Nuave达到最大值以后,颗粒融化的Nuave由于颗粒速度的下降而逐渐减小,且由于不同工况下颗粒浮升速度的变化趋势不同,颗粒融化的Nuave下降的趋势也不同.与图3速度变化图相对应,颗粒速度减小的越快,Nuave下降的就越快.这是因为颗粒运动速度大代表颗粒与流体之间的相对速度大,颗粒周围的流场扰动增加,增强了颗粒与流体之间的对流换热作用.
在工况3下颗粒浮升融化的液相场和温度场的分布如图7所示.为方便对比分析,选取了与图4相同的3个无量纲时刻.可以看到由于初始时刻颗粒内部有3 K的过冷度,在t*=0.015时冰晶颗粒内部有明显的温度分布,说明此时从流体传递到颗粒的热量并没有全部用来使颗粒融化,而是有一部分通过导热进入颗粒内部使颗粒温度上升.另外,由于糊状区域常数的影响,在θ=100°附近产生了固液相界面的畸变.与工况1相对比,可以看到右侧坐标对应的颗粒浮升的距离有所增加,这是因为相同时刻下工况3中冰晶颗粒的浮升运动速度大于工况1下的浮升速度(见图3).工况3下颗粒的总融化时间增加,相同的无量纲时间下浮升的实际时间较长.
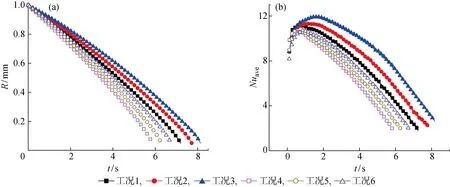
图6 不同工况下的颗粒半径变化以及平均换热系数对比Fig.6 Variation of particle radius and average heat transfer coefficient over time in different cases

图7 工况3下不同时刻的液相场及温度场分布Fig.7 Distribution of liquid phase and temperature at different instants in Case 3
4 结论
本文采用焓-多孔介质法对冰晶颗粒的非均匀融化过程进行了数值研究,并采用液相分数追踪固液界面,研究了不同的换热温差条件下以及颗粒内部有无过冷度的条件下颗粒的浮升融化过程,得到以下结论:
(1) 冰晶颗粒在浮升融化过程中先加速至速度最大值,然后开始逐渐减速直至颗粒融化完全.颗粒减速过程的速度变化与颗粒尺寸的变化有关.由于速度场和温度场的耦合作用,冰晶颗粒各个位置融化速率不同,颗粒的形状发生不规则的变化,由圆形逐渐变化为椭圆形,最后变化为不规则的方形直至融化结束.
(2) 增加颗粒与流体之间的换热温差能够减少冰晶颗粒的融化时间,而初始情况下颗粒内部过冷会造成冰晶颗粒的融化时间增加.这是由于增大温差相当于增大了换热驱动势,而在有过冷度的条件下有一部分热量被传递至颗粒内部用于颗粒显热升温.
与以往的研究相对比,本文提出了以焓-多孔介质法来捕捉颗粒与流体两相之间的界面移动和变形,对颗粒运动过程中的非均匀融化过程进行了研究,考虑了颗粒内部过冷对颗粒运动融化的影响,捕捉到了颗粒融化过程中颗粒内部的温度变化情况,为研究固液两相的之间的作用规律提供了新思路.
