考虑广义时间价值的串行退化生产系统维护更新策略
2020-06-06李雨青张秀芳潘尔顺
杜 煜,李雨青,张秀芳,潘尔顺
(上海交通大学 机械与动力工程学院, 上海 200240)
随着现代制造类企业生产规模的不断扩大,对生产系统的稳定性和可靠性的要求越来越高,因此,良好的维护和更新策略对于生产系统的健康运行有着至关重要的作用.串行系统是一类常见的生产加工系统(如汽车发动机5C件生产线),对于多工序流水生产线,机会维护策略可以有效节省因设备维护产生的停产损失,提高生产的连续性,故采用机会维护策略进行维护,并在维护策略的基础上制定系统的更新策略.关于多设备系统的维护策略,许多学者进行了研究.余佳迪等[1]以带缓存的两设备串行系统为研究对象,考虑上下游设备同时故障的情况,构建了系统总成本最小的设备预防性维护模型.Lu等[2]针对具有中间缓冲的多设备串行系统进行了建模优化.以上研究均考虑缓存空间,但没有考虑设备退化时引起的次品率上升的问题.陶红玉等[3]用Gamma分布描述设备的退化过程,构建了随机退化串行系统的机会维护模型,并确定了最优检测周期,但其结果是在设备退化量被定周期连续监测的条件下求得,且设备服从同一退化分布,很难与实际相符.候文瑞等[4]以串行生产系统为研究对象,采用机会维护策略,利用费效比决策系统内设备的维护更新行为,但在计算成本时仅考虑了系统维护时的成本,未考虑生产引发的成本,也未对维护阈值进行优化决策,且其系统可能存在可用度过低的风险.Zhou等[5]通过最小化系统成本,对串行系统提出了基于机会维护下的预防性维护算法.Xia等[6-8]提出了多特征值模型,在同时考虑成本及可用度两个目标函数前提下,决策设备最优的预防性维护周期.通过设定维护时间窗,动态地利用混联系统中的维护机会,从而实现缩减系统成本的目的,并且提出联合生产计划以及预防性维护的调度问题,通过机会维护方式,降低了系统维护成本.以上研究的不足之处在于,均未考虑广义时间价值的作用.
在制定设备的更新策略时,大多数生产企业仍然采用以固定的工作年龄、故障次数或维护次数为依据的传统策略,主要采用更新过程定理和平均成本率最低的方法.贾积身等[9]针对修理工单重休假的可修系统,比较了以工作时间和故障次数为依据的更新策略,但现实中修理工往往会轮班,不存在休假,故实际应用意义不大.Gao等[10]利用更新过程理论,研究了具有两类故障模式(可修和不可修)的单机系统,求出了长期运行单位成本最低的维护次数,但未考虑系统可用度的变化.Song等[11]研究了受限于δ随机冲击的退化系统最优更新策略,将系统维护时间和失效机制分别假设成几何过程和δ冲击过程,以长期运行单位成本最低为目标求解最优维护次数,但仍未考虑系统可用度的变化.Wang等[12]研究了具有定周期检测和随机故障的可修-替换系统,结合更新过程决策使系统成本率最小的检测时间和故障次数,但假设维护行为是对设备年龄的影响,而不是对退化状态的影响.Zhao等[13]针对某施工企业混凝土搅拌车基于网络模型,将设备更新问题转化为图论的最短路径问题,解决了设备更新方案的选择问题,但是该方法并没有考虑不同维护策略下的改变.Chang[14]提出了工作时间-故障类型的二元更新策略,并且对该模型进行了二次延展,进而给出了延展模型的最优预防性维护排程.类似地,以上文献提出的更新策略均未考虑广义时间价值的作用.
设备的广义时间价值(generalized time value, GTV)指的是随着技术进步,市面上出现了性能更优、效率更高以及经济性更好的设备并被广泛采用,导致企业当前设备的重置成本降低,使用费用相对变高,所生产商品的竞争性下降,最终致使设备在因老化失效无法完成规定功能之前,用新设备代替旧设备成为必然,因此缩短了设备的服务寿命.目前,针对设备具有广义时间价值的问题,对相关维护更新策略进行数学分析的研究尚属空白.
鉴于此,本文提出了一种全新的考虑广义时间价值的串行退化生产系统维护更新策略.首先建立设备层维护模型,将设备的维护时间看作关于设备退化度和维护次数的函数,提出退化度恢复因子;随后根据考虑广义时间价值的设备维护成本、维护效果以及设备可用度决策设备的维护更新行为,建立系统层维护更新模型.算例仿真对设备维护阈值进行了优化决策,并给出了系统的维护排程以及各组成设备的更新时间,证实了广义时间价值对串行退化系统内设备更新时间的影响.
1 问题描述与假设
串行生产系统如图1所示.系统由n台设备串联而成,分别负责n道不同的工序.工序之间不设置缓冲站,且负责不同工序的设备不同.设Ex为负责系统第x道工序的设备,当设备Ex停机时,整个系统停机.采用机会维护策略对系统进行维护,维护行为主要包括:预防性维护,机会预防性维护(简称机会维护),设备更新以及设备机会更新.其中预防性维护和机会维护均为不完美维护(如除尘、润滑、更换部分零配件等),只能使设备的退化状态在一定程度上得到恢复,不能使设备恢复如初.更新和机会更新均为完美维护,即用新设备替换旧设备或用新部件替换旧部件,使其恢复如新.当系统运行至某一时刻t,设备Ex的退化度Fx第i次到达预防性维护阈值DPM,系统须停机对设备Ex进行预防性维护或者更新.与此同时,对退化度达到机会维护阈值DOM的其他设备进行机会维护或者机会更新.DPM和DOM可以通过分析历史运行数据得到,也可以通过设定目标函数优化求得.研究串行生产系统在该机会维护策略下的维护排程,各组成设备的更新时间以及广义时间价值对设备更新时间的影响是本文的主要研究目标.

图1 串行生产系统模型Fig.1 Model of series system
假设:
(1) 串行系统中的所有组成设备在正常工作中的突发性故障用小修恢复,小修不改变设备的退化状态,仅恢复设备功能,且时间和费用很小,可忽略不计.
(2) 串行系统各工序在任意时刻的生产能力均保持平衡,除设备维修维护和更新外,系统无停机.
(3) 设串行系统所有组成设备的生产能力保持不变,设备生产的在制品中出现次品的概率与该设备的退化度成正比.
则有:
式中:rx(t)和Fx(t)分别表示设备Ex在t时刻的次品率和退化度.
2 设备层维护策略建模
2.1 设备层退化模型
Gamma过程为随机退化过程提供了有效工具,本文采用Gamma过程对设备的退化进行建模.Gamma过程具有以下特性:
(1)X(0)=0;
(2) {X(t),t≥0}具有独立稳定的增量;
(3)对于任意的t>0,Δt>0,
ΔX(t)=X(t+Δt)-X(t)~Ga(αΔt,β)
其中:X(t)为退化量;α为形状参数,β为尺度参数,满足α>0,β>0;G(αΔt,β)为Gamma分布密度函数,
G(x|αΔt,β)=
Δt为时间差;Γ为Gamma函数,且有

为指示函数,当x∈(0,∞)时,I(0,∞)(x)=1,其他情况为0.
对于一台设备而言,当其退化量达到某一事先预设的阈值后就会失效.设设备Ex的退化量阈值为dx,在t时刻的退化量为Xx(t),将设备Ex在t时刻的退化度Fx(t)定义为Xx(t)>dx的概率,具体可用下式表示:
(3)
式中:fXx(t)(x)=G(x|αt,β)表示t时刻设备Ex退化量的概率分布密度函数.
2.2 设备层维护模型
2.2.1维护效果 如图2所示,设备每次维护后的退化度应不低于设备前一次维护后的退化度,引入退化度恢复因子ε,第i次预防性维护对设备Ex的维护效果可表示为
(4)

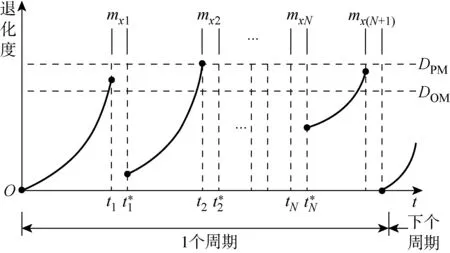
图2 设备退化度演化模型Fig.2 Evolution model of degradation degree
2.2.2维护时间 预防性维护时间的长度通常依赖于F(t),并与设备已经历的维护次数i有关.一般而言,相较于一台年轻设备,维护一台严重老化的设备需要消耗更多的时间.因此,设设备Ex第i次预防性维护的时长mx i可表示为
(5)
式中:h,b为维护时间参数,且满足0
3 系统层维护更新策略建模
3.1 维护策略
假设串行系统在ti时刻有设备的退化度达到DPM,系统进入第i次停机维护,引入维护因子axi判别设备Ex在第i次系统维护时是否需要维护或者更新:
(6)
式中:ax i=1表示设备Ex需要进行维护或者更新;ax i=0表示设备Ex不需要维护或者更新.再引入状态因子ωx i判断设备Ex采取的维护方式:
(7)
式中:ωx i=-1表示设备Ex停机,ax i=0时必然有ωx i=-1;ωx i=0表示设备Ex进行更新或机会更新;ωx i=1表示设备Ex进行预防性维护或机会维护.ωx i具体如何决策将在3.3节中详述.结合ax i和ωx i可得设备Ex在系统第i次停机维护过程中需要占用的维护时长mx i为
(8)
式中:px为设备Ex所需的更新时长:φx i表示系统第i次停机前,设备Ex已进行的预防性维护次数.经推导φx i满足关于i的递推数列:
(9)
系统第i次停机维护的时间Mi取决于所有待维护或更新的设备中所需耗时最长的设备.将所有设备的维护时间mx i写成矩阵的形式Ai,则Mi为矩阵Ai中的最大值:
对设备Ex在系统第i次停机维护前后的退化度Fx(t)变化进行推导.
(1)axi=0,ωxi=-1,设备Ex停机,则Fx(t)变化如下:
(12)

(2)ax i=1,ωx i=0,设备Ex更新或者机会更新,则Fx(t)变化如下:
(13)
(3)axi=1,ωxi=1,设备Ex进行预防性维护或者机会维护,则Fx(t)变化如下:
(14)
经推导,Txi满足关于i的递推数列:
(15)
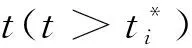
Fx(t)=
(16)

(17)
式(17)中的其他参数可以从系统的维护记录中获得,则设备Ex在任意时刻的退化度均可求出.
3.2 维护成本
维护成本一直是生产系统维护更新策略中用来衡量策略表现的重要指标,从不同的角度考虑,其所包含的项目不同.如果不考虑广义时间价值,本文中设备Ex的维护成本包括预防性维护成本、更新成本、停产损失成本以及次品成本.如果考虑广义时间价值,维护成本除了以上提到的项目还包含:① 因设备重置成本持续降低导致单位时间折旧费用增加的成本;② 因技术落后导致的单位时间生产费用上升的成本;③ 因技术落后导致系统生产的商品缺乏竞争力,致使单位商品利润率下降的成本.


(18)

(19)


(20)
(3) 设备Ex在t时刻次品率的表达式为rx(t)=rFFx(t).故系统生产出次品在设备Ex分摊额为
(21)
(4) 设备的折旧时间不仅包含工作时间,还包含维护时间和停机时间,故设备Ex因广义时间价值增加的折旧费用为
(22)
(5) 设备Ex由于广义时间价值增加的生产费用为
(23)
(6) 由于次品不能用于销售,在计算产成品利润时需要减去.故系统所生产商品的利润下降额在设备Ex上的分摊额为
(24)
综上,考虑广义时间价值,系统第i-1次停机维护结束至第i次停机维护结束期间,设备Ex的总维护成本Cxi可表示为
(25)
3.3 更新策略
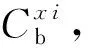
(26)

(27)
通过对比设备Ex进行预防性维护和更新时Kxi的大小,即可对ωxi的取值进行决策,同时还要考虑设备Ex可用度的变化.设备可用度表示设备在一段时间内工作时间与总时间的比值,由于在本文中,设备的停机是由于其他设备需要进行维护,系统无法进行生产造成的,并非出自自身原因,故这里没有将设备的停机时间计入总时间,设备Ex在ti时刻的可用度Axi可表示为
(28)
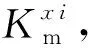
(29)
则依次可得到该串行生产系统各设备在系统每次维护时的维护行为,进而得到各设备的更新时间.
4 算例分析
4.1 算例建模与求解

图3 串行生产系统示意图Fig.3 Structure of series system
本文以某发动机零部件串行生产系统为例,对以上维护更新策略进行数值分析.该生产系统有负责5道不同工序的5种不用类型的设备,分别为磨床、车床、铣床、辊压机床和抛光机,该串行生产系统模型及设备编号如图3所示.各设备的退化过程服从参数不同的Gamma分布,根据生产实际以及部分参考文献[3-4],设置:
ε=0.85,rF=50%
h=5,b=0.95
px=5 d (x=1,2,…,5)
A0=0.6,Ld=10 000
d=100件,cpro=100元


其他维护与成本参数见表1.
首先对设备的DPM和DOM进行优化决策,以串行生产系统500天内的所有设备的维护成本和Csys为优化判据,Csys可表示为
(30)

表1 维护与成本参数Tab.1 Parameters of maintenance and cost

表2 预防性维护计划Tab.2 PM schedule
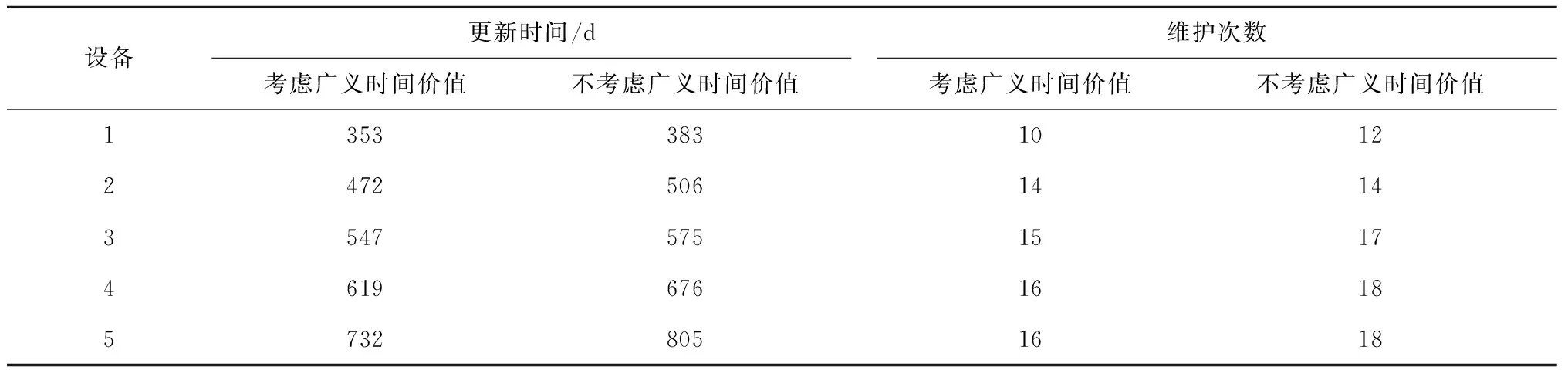
表3 设备更新时间与维护次数Tab.3 Replacement time and PM times
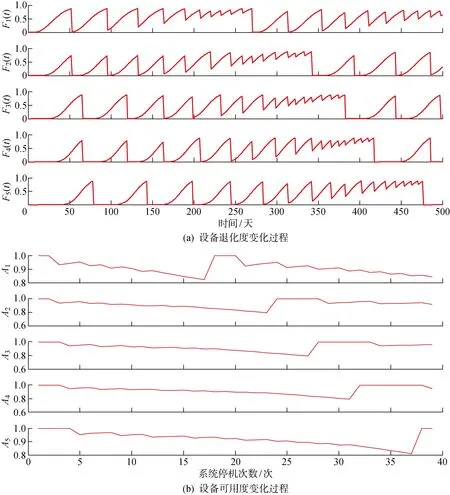
图4 设备退化度与可用度变化过程Fig.4 Evolution of degradation degree and availability
取使得Csys最小的阈值组合(DPM,DOM)作为该串行系统维护阈值.采用MATLAB编程计算,通过遍历DPM∈[0.1,0.9],DPM∈[0.1,DPM]内的所有组合得到使Csys最小的阈值组合为DPM=0.85,DOM=0.7,所得的最小成本Csys=347.69万元.
令DPM=0.85,DOM=0.7,采用MATLAB编程计算得到该串行生产系统在所有设备均完成一次更新前的维护工作排程如表2所示(由于篇幅有限,只列举了系统前4次停机和有设备更新时的维护排程).表中:1代表预防性维护和机会维护;0代表更新;空白代表停机;…代表省略的维护排程.各工序设备的首次更新时间以及更新前经历的维护次数如表3所示.各设备的退化度随时间的演变过程以及可用度随维护次数的演变过程如图4所示.
4.2 结果分析
由图4可知:所有设备的更新原因在于Km>Kp,设备可用度均未超出限值.分析表3可知:负责不同工序的设备,其更新时间均相差较大,说明针对串行生产系统的更新策略应该针对单台设备具体实施,此操作比系统整体更新的策略更加准确.
由表3可知:不考虑广义时间价值下,各设备的更新时间均大于考虑广义时间价值下的值.进一步说明,广义时间价值会加速设备的老化,缩短设备的使用寿命.
5 结语
考虑广义时间价值,针对串行退化生产系统进行了维护更新策略的研究.提出了设备层维护模型以及系统层的维护更新模型,算例仿真优化了设备维护阈值,证实了广义时间价值会加速设备的老化,缩短设备使用寿命的作用,为企业制定串行系统维护更新策略提供了新的尝试.然而,本文在建立生产系统模型时未考虑缓存空间的作用,故还有待进一步深入研究.
