模型-数据联合驱动的船舶舵机电液伺服系统早期故障检测

徐巧宁，艾青林，杜学文，刘 毅

(1. 浙江工业大学 特种装备制造与先进加工技术教育部重点实验室， 杭州 310023；2. 浙江大学宁波理工学院 机电与能源工程学院， 浙江 宁波 315100)

船舶舵机电液伺服系统主要用于控制船舶运动和航向，一般情况下，船舶出海时间长且海上工作环境恶劣，因此保持舵机电液伺服系统正常、稳定地运行，对于船舶的安全航行至关重要[1-2].船舶舵机电液伺服系统是集机械、电气和液压为一体的复杂非线性系统，且其工作环境恶劣多变，由于各类不确定因素的存在，早期故障信息往往会被掩盖，不易发现.因此，要对船舶舵机电液伺服系统的故障，特别是早期故障进行有效的检测和判断，该工作具有较大的挑战性[3-4].

一方面，基于模型的故障检测方法采用解析冗余代替硬件冗余，应用较为广泛，然而该方法对模型的精确性要求较高[5].舵机伺服系统本身为一个复杂非线性系统，系统中存在诸多如水动力负载、摩擦负载以及未知参数等不确定因素，所造成的模型不确定会严重影响故障检测结果.因此，如何对模型不确定性进行有效处理，提高故障检测的鲁棒性，同时保持故障检测的敏感性一直以来都是各国学者研究的热点[6-7].Sepasi等[8-9]采用事先测量或算法估计来获取摩擦力、外干扰力的值及变化范围，以提高模型精度，从而增加故障检测的准确性，该方法的局限性在于如果外干扰是时变且无规则的，则难以准确获得.另一类方法是先将系统模型看作为准确模型，然后构建相应的观测器/过滤器，将得到的输出残差作为随机变量数组，采用鲁棒故障决策的方式提高鲁棒性，如Khan等[10]采用Wald序贯检验来判断系统中有无故障，Shi等[11]采用自适应阈值进行故障判断.需要注意的是，如果不确定干扰对残差的影响是否大于故障，那么一些早期故障信息将被掩盖.还有一类方法则是采用鲁棒故障检测观测器，该方法产生的残差只对故障敏感而对干扰鲁棒，有利于早期故障检测，如Bahrami等[12]采用自适应观测器，Palli 等[13]采用滑模观测器对电液系统故障进行检测与重构[12-13]，该类方法一般有一定的使用限定条件.此外，系统中还存在诸多非结构化不确定性等，早期故障检测时需要考虑[14].

另一方面，计算机技术的飞速发展使得采集和存储大量数据成为可能，因此基于数据驱动的故障诊断方法也得到了长足的发展[15-16].如，Sharifi等[15]采用神经网络，He[16]等采用模糊自回归，Fu等[17]采用了同胚映射，配合适当的故障特征提取方法来进行系统故障诊断.基于数据的方法可实现难以建模系统的有效故障诊断，与基于模型的方法形成了有效互补，是近年来的研究热点.然而，要获得各类故障特征样本进行事先学习训练并非易事，一旦系统中存在未知项和干扰项，则训练的难度将大大增加[20].

本文结合了基于模型和数据方法两者的优势，提出了一种模型-数据联合驱动的故障检测方法，详细考虑了系统中的各类不确定因素，并逐层分步对其进行了处理.通过本文所提混合式方法，可保证对干扰的鲁棒性并提高对故障的敏感性，从而实现早期故障的有效检测.

1 舵机电液伺服系统建模与分析

1.1 系统简介

常见的阀控型船舶舵机电液伺服系统如图1所示，该系统包含自动和手动两种操作模式，通过隔离阀10进行切换，比例阀7和液动操舵阀8分别在两种模式下进行舵机油缸的控制.当隔离阀处于左位，系统处于自动控制模式，通过比较实际舵角和指令舵角，由控制器计算得到相应的输出控制信号，该信号输入比例阀电控端，通过控制比例阀阀芯的位移来控制进出舵机油缸的油液流量，从而控制舵机油缸活塞的运动，舵机油缸的位置信号又通过齿轮齿条机构转变成转角信号，由编码器采集输入控制器，周而复始，最终达到指令舵角，进行船舶航向的控制.实际船舶舵机中舵机油缸的活塞杆通过一系列机械结构与舵叶相连，舵叶则承受着各种水动力负载，在实验系统中，舵机油缸活塞一般与加载系统相连，通过加载系统进行负载模拟对其进行加载.

1.2 系统分析与建模

针对系统的自动控制模式进行研究，依据与电液控制系统建模相关的理论[21]，建立各部分的系统方程.

流体比例阀的流量方程表示如下：

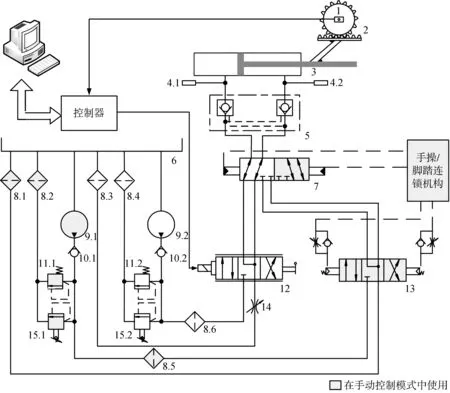
1—角度传感器, 2—齿轮齿条, 3—舵机油缸, 4—压力传感器, 5—液压锁, 6—油箱, 7—隔离阀, 8—过滤器, 9—定量泵, 10—单向阀, 11—安全阀, 12—比例阀, 13—液动操舵阀, 14—节流阀, 15—溢流阀图1 船舶舵机电液伺服系统原理图Fig.1 Schematic diagram of the RESS

(1)

式中：q+与q-分别为进出液压缸无杆腔和有杆腔的流量；kq为流量系数；xv为比例阀的阀芯位移；w为比例阀的死区；ps+与ps-分别为供油和回油压力；p+与p-分别为油缸无杆腔和有杆腔的压力.比例阀的动态方程可用一阶模型表示为

(2)

式中：τ与kv分别为描述比例阀动态特性的时间系数与增益系数；u为输入电压.

液压缸的流量连续性方程为

(3)

式中 ：a+与a-分别为液压缸无杆腔和有杆腔的面积；xp为舵机油缸活塞的位移；ci与ce分别为液压缸的内外泄露系数；V+与V-分别为液压缸无杆腔和有杆腔的有效容积；βe为油液的有效体积弹性模量.液压缸和负载的力平衡方程为

(4)

式中：m为负载及折算到负载上的总质量；bp为粘性阻尼系数；f为其它外负载，包括水动力负载，惯性负载、摩擦负载及干扰负载等，实际系统中的粘性力及外负载是未知时变.

(5)

式中：A,B,C,D为系统的参数矩阵，

d为系统的干扰项

g(x)为系统中的非线性项

g±(xv,p±)=

1.3 故障分析与建模

通过分析图1的船舶舵机电液伺服系统可知，常见的执行器和元件故障包括系统供油压力异常(Δps+)，舵机油缸内泄漏(Δci)，比例阀故障(Δkv)以及角度传感器故障(Δθ)，舵机舵角θ=kdxp，kd为舵机油缸的位移转换成角度的比率.因此，含有故障项的系统状态方程可表示为

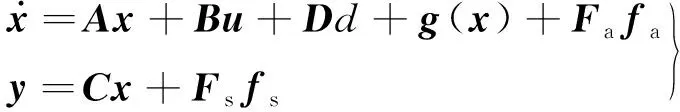
(6)

式中：Fa和Fs为分别为执行器和传感器的故障定位矩阵，

1.4 模型不确定性分析

正如其他基于模型的系统研究一样，所建立的船舶舵机电液伺服系统也难以避免模型的不确定性，总的来说，该系统的不确定性主要包括以下几个方面.

(1) 参数的不确定性，液压系统中的一些参量在不同的工作环境下是不同的，比如βe，ci，ce以及kq等，对于每一个液压系统，这些参数的具体数值都会有所不同且一般为未知数.有些采用实验测量的方式获取这些值，但是这些实验操作起来比较复杂，而更多的则采用经验试凑的方式.试凑的方法一般先根据经验定几个初值，再通过与实际系统的相应输出参量比对来不断调整，由于舵机电液伺服系统中不只有一个未知参数，因此具体调哪个，每个调整值为多少均为位置，该过程一般需要花费大量的时间精力，存在很大的不确定性，且估算结果的准确性会影响系统的早期故障诊断.

(2) 实际的船舶舵机在水中承受的外负载包括水动力负载，惯性负载，摩擦负载, 浪涌和舵面空拍干扰负载等，这些外负载力学关系复杂，往往是未知和时变的，且难以准确测得，再加上舵机油缸运行时的粘性阻尼力和摩擦力等，对于系统来说相当于存在未知时变的输入项，这些未知力会引起系统状态量的变化，对系统故障的判断造成混淆，因此会对系统的故障诊断带来很大的挑战.

此外，其他难以通过建模描述的不确定性如系统的固有非线性、非结构化模型不确定性、干扰、噪声等，也会影响早期故障检测.

2 舵机电液伺服系统故障检测

2.1 不确定参数辨识

正常状态下的系统模型往往会作为标准来进行故障检测观测器、滤波器的构建，因此，正常系统模型的准确性非常重要，要能保证相同输入下模型输出和系统输出的一致性.由式(5)可知，系统中主要不能确定的参数包括βe,kq,ci和ce，为了能够进行下一步的故障检测，需要获得这些参数值，考虑到实验测量这些参数时存在困难，而若以经验试凑的方式面对4个参量的调整，不仅费时费力，而且存在较大的偶然性.因此，提出在系统数学模型的基础上，采用正常状态下系统的输入输出数据对这些参数进行辨识.

由式(5)可得到：

Φθ=Γ

(7)

式中：

定义标准函数为

(8)

(11)

2.2 鲁棒故障检测观测器构建

假设1对于非线性项g(x)，存在一个正常数γ使下式成立：

(12)

评述在船舶舵机电液伺服系统中的非线性项即使不是全局Lipschitz的，至少也可以看成是局部 Lipschitz 的，因为系统的状态变量是有界的[24].

假设2传感器发生的是渐变故障.

评述这类故障在系统中较常见的，如传感器的逐步零漂和增益变化，且这类故障一般难以察觉.

图2 故障检测观测器框图Fig.2 Block diagram of fault detection process

依据基于模型的故障诊断技术理论及故障检测观测器设计理论[25-26]，针对船舶舵机电液伺服系统，由图2构建的非线性未知输入观测器如下：

(13)

式中：N=TA-KC；G=TB；L=K-NE；T=I+EC，I为单位矩阵.

如果式(13)是式(6)的故障检测观测器，那么必须满足以下3个要求：

(2)d变化不会影响残差；

(3) 当fa或fs变化时会引起残差变化.

理论1如果存在两个矩阵E,K和1个对称正定矩阵P使得以下3个条件得到满足：

TD=0

TFa≠0or (NE+L)Fs≠0

NTP+PN+γPTTTP+γI<0

则式(13)是式(6)的一个故障检测观测器.

T[Ax+Bu+Dd+g(x)+Fafa]=

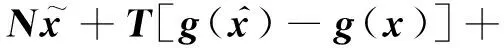
(G-TB)u-TDd-TFafa+

(NE+L)Fsfs+(N+NEC+LC-TA)x

(14)

根据式(13)各参数矩阵的表达式可得G=TB，N+NEC+LC=TA，因此

TFafa+(NE+L)Fsfs

(15)

由上式可知，如果TD=0，则d变化将不会影响残差，与故障检测观测器的要求②相对应，因为D为列满秩，如果rankCD=rankD，则由TD=0可以解得

E=Ea+YEb

(16)

式中：Ea=-D(CD)-1；Eb=I-(CD)(CD)-1且(CD)-1=[(CD)T(CD)]-1(CD)T.

(17)

(18)

上述不等式一般很难直接求得，可以根据Schur 补引理，将上式进行调整，采用线性矩阵不等式(LMI)的方法进行求解[27-28]，计算过程如下：

(1) 根据式(CD)-1计算Ea和Eb.

(19)

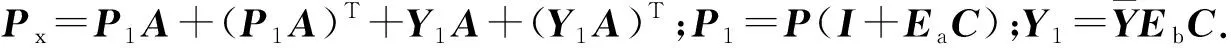
(4) 计算观测器的参数矩阵N=TA-KC，G=TB，L=K-NE和T=I+EC.

2.3 基于神经网络的补偿方法

通过上述步骤，尽管系统的不确定参数得到了初步辨识，且系统的非线性和未知外负载得到了处理，但是，实际系统正常状态下的故障检测观测器输出依旧会呈现非零状态，这主要是因为系统中还存在诸如难以建模的非结构化不确定因素，以及干扰噪声等剩余不确定部分.这些剩余不确定因素会覆盖系统故障信息，造成混淆，尤其使得一些早期故障难以被发现，因此需要进行补偿处理.

考虑剩余不确定因素后系统正常状态下的模型可表示为

(20)

式中：Λ(x,u,t)，γ(u,t)分别为建模不确定性和测量不确定性，t为时间.

由上式可得到

[Bu(τ)+Dd(τ)+g(x(τ))]dτ+

(21)

x(t)=C-1y(t)-C-1γ(u,t)

(22)

通过式(21)和(22)可知，消除x后，该式变成1个有关系统输入、输出和不确定项的关系式，完全解出此关系式存在一定难度，但该式也说明了系统中的不确定部分和系统的输入输出存在一定的关系，即可以用系统的输入输出来表示剩余不确定部分.此外，还可知，系统的输入输出和剩余不确定部分关系复杂，存在强非线性，一般的建模和估计算法难以实现系统输入输出到剩余不确定部分的计算.近年的研究表明，神经网络对于未知连续函数具有很好的逼近能力，特别适用于难以进行传统建模的场合[29-30].因此，利用系统输入输出，采用神经网络的方式对系统剩余不确定性的影响进行模型补偿是可行的.

为了有效描述剩余不确定性对残差的影响，用于训练补偿模型的数据应采用不受故障影响的状态量.由于不受所有故障影响的状态量难以获得，所以需要针对不同情况建立多个补偿模型.对于执行器故障来说，第i个补偿模型的输入为系统正常状态下的ui和y，其中ui代表除第i个输入外的所有系统输入，y代表所有系统输出；对于传感器故障来说，第j个补偿模型的输入为u和yj，其中u代表所有系统输入，yj代表除第j个输入外的所有系统输出，图3所示为神经网络补偿模型的构建过程.

图3 神经网络补偿模型构建框图Fig.3 Block diagram of fault detection with compensation models

通过模型补偿正常状态下输出的残差趋于0，而存在故障时输出残差会发生偏离.对于执行器故障，由故障项引起的残差偏差量为

(23)

式中：

同理可得，当t→∞时，由传感器故障引起的残差偏差量为

其中故障参数矩阵

2.4 舵机系统早期故障检测总体方案

将上述几类不确定因素处理方法进行有效组合，可形成系统总体早期故障检测框图如图4所示，该系统数据库中的数据仅需正常运行状态下的系统输入输出数据即可.该方案将基于模型的故障检测方法与基于数据的辨识构建方法相结合，在保留故障信息的基础上，对系统的不确定干扰因素进行了逐层削减，以减少对故障信息的影响，从而实现早期微小故障信息的有效检测.

图4 模型-数据联合驱动早期故障检测框图Fig.4 Flow chart of the integrated model-based and data-driven fault detection algorithm

3 仿真与实验研究

3.1 仿真与实验系统建立及参数辨识

在实验系统及MATLAB环境中搭建的仿真系统中验证故障诊断方法的有效性，实验系统如图5所示.图5右下角为进行船舶舵机电液伺服系统故障诊断研究的实验台，舵机油缸的活塞杆上连接 4 000 kg的质量块，以进行负载模拟.一般的船舶舵机系统控制器是专门定制的，不能随意改变，以保证可靠性，因此所增加的在线故障诊断系统不能影响原系统的控制和运行.基于上述原因，如图5所示系统中单独搭建了基于NI-PXI系统的数据采集和故障诊断系统，与原系统并行运行，该系统的主要模块包括：双核控制器(PXIe-8108 RT)，多功能I/O模块(PXI-6229)，PXI机箱(PXIe-1071)及相应附件等.实时采集的信号包括指令和实际舵角信号，舵机油缸两腔的压力以及控制器的输出电信号，采样率为1 kHz，该系统的相应参数如表1所示，其中dp为舵机油缸内径,dr为活塞杆杆径,ld为舵机油缸的有效行程，Ln为比例阀的名义流量.

图5 船舶舵机电液伺服系统实验台Fig.5 Experimental test rig of RESS

表1 船舶舵机电液伺服系统的参数

Tab.1 Parameters of the ship rudder electro-hydraulic servo system

参数数值dp/mm260dr/mm100ld/mm380V+/m30.0104V-/m30.0089Ln/(L·min-1)100w/mm0.3kv/(mm·V-1)0.5τ/ms12.5m/kg4000ps+/MPa3ps-/MPa0.1kd/(mm·(°)-1)7.6

3.2 正常状态下的检测性能

为验证所搭建系统及辨识参数的有效性，将表1中的系统参数以及辨识得到的系统参数均代入系统模型式(5)中，同时将力，速度系数设置为6×105N/(m·s-1)，在实验和仿真系统中输入相同的指令舵角信号，得到的系统输出，如图6所示.

由图6可知，仿真结果与实验虚线吻合，说明所搭建模型及辨识得到参数与实际相符；通过图6(e)、6(f)即液压缸两腔压力局部放大曲线可发现，虽然仿真结果与实验曲线整体趋势一致，但是由于实际系统存在的各种摩擦、干扰以及运行过程中的力波动等问题，难以对外力进行准确估计，仿真曲线不可能完全与实际曲线吻合，在实际舵机系统中外负载力还包括其他未知时变的水动力负载，浪涌和舵面空拍干扰负载等，这些都将影响早期故障的诊断，由此也验证了最初的设计想法，即无需测量或估计外负载力，只是将其作为未知干扰项进行解耦处理.因此，在后文的观测器搭建过程中未对粘性阻尼力、摩擦力等其它干扰力进行过任何估计，也无需获取过其变化范围，在所受力信息缺失的情况下，实现系统的鲁棒故障检测.

图6 实验测量和仿真输出结果Fig.6 Measured and simulated results

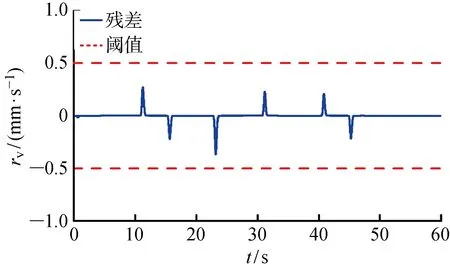
图7 仿真正常状态下输出残差Fig.7 Simulated observer performance in normal state

图8 实验正常状态下输出残差Fig.8 Experimental observer performance in normal state

依据2.2节所述，可设计船舶舵机电液伺服系统鲁棒故障检测观测器，将系统正常状态下活塞的实际输出速度与观测器估计输出速度做差值，可得如图7所示的速度输出残差(rv).由图7可见，在整个运行过程中，残差几乎为0，只有一些小的毛刺，这些小毛刺主要出现在启停和突然换向过程中，在仿真中可以通过设置上下固定阈值(±0.5 mm/s)来进行故障决策.

图8所示为实验得到的正常状态下输出速度残差，v+与v-分别表示活塞运动的两个方向.由图可见，实验曲线与仿真曲线整体趋势一致，除在启停换向时会有毛刺，其它阶段在0值附近波动，这说明了之前辨识得到的参数的有效性以及所构建的故障检测观测器在正常状态下的有效性.然而，与仿真曲线比较，相较于仿真输出，实验输出残差与零值的偏离量和波动性均较大，这也说明了实际系统中依然存在剩余不确定性和干扰，这些不确定性将会影响故障诊断的结果，尤其影响早期故障的发现.

由于图8中实际系统呈现的毛刺造成的残差幅值变化较大，因此不能采用图7仿真中的固定阈值，为避免故障的误判同时保持对故障的敏感性，设计了如下自适应阈值进行故障决策：

(24)

k=1,2,…

图9 正常系统在不同外干扰力下的输出残差Fig.9 Forces and residuals in normal state

图8中的虚线表示自适应阈值，可见，采用自适应阈值后，残差曲线均在阈值范围内，因此表示系统正常无故障.

由图9可见，无论外干扰力如何变化，所输出的速度残差基本不发生变化，除了在启停换向瞬间有些小毛刺，其余几乎为0，且在阈值范围内，不会造成误报警.由此也验证了所提出的故障检测方案对未知时变干扰力的鲁棒性.

表2 自适应阈值参数设置Tab.2 Parameters setting of adaptive threshold

3.3 故障状态下的检测性能

为检验所提出方案的故障检测性能，在仿真和实验环境分别设置了4类常见故障，方法如下：

(1) 供油压力异常故障.将溢流阀的设定压力由3 MPa调为2.8 MPa.

(2) 舵机油缸内泄漏故障.在进出舵机油缸两腔管路间加上1个内径3 mm的节流孔来模拟(在仿真系统中将内泄漏系数由0.01 mm3/(s·Pa) 设置为0.1 mm3/(s·Pa)).

(3) 比例阀故障.比例阀的输入设为0.9u.

(4) 角度传感器故障.角度传感器的输出设为0.87θ.

上述几类常见故障会造成舵机不能达到指定舵角，或者转舵慢等问题，而在故障初期，这些现象并不明显，再加上系统中各类不确定因素以及干扰的混淆，很难进行系统有无故障的判断，在故障值的设置上，尽量小的偏离标准值，以模拟早期故障参量偏离状态.

上述4类故障检测的仿真和实验结果分别如图10和11所示.

图10 故障检测仿真结果Fig.10 Simulated fault detection performance

可以看出，图10中4类故障的输出残差曲线在活塞的两个运动方向上v±均超出了阈值，说明所有故障均可得到有效检测，从仿真上验证了所采用的故障检测方法的有效性；将图11与图8正常状态下实验输出残差相比较发现，发生4种故障后，实验得到的残差曲线在活塞两个运动方向上均发生了偏离，且偏离的方向与图10仿真曲线一致，由此也从实验上验证了所采用的故障检测方法的有效性；与图10的仿真结果不同，虽然图11中所有故障残差曲线发生了偏离，但是这些残差却很难超过阈值，即故障不能全部得到有效检测.这是因为实际系统不像仿真系统那么理想，存在着剩余不确定干扰，而所设置的故障偏差又很小，属于早期故障，因此这些故障信息被系统的剩余不确定干扰所覆盖了，实验发现，如果进一步加大故障偏差量，则所有故障均可超出阈值得到检测.

针对上述早期故障敏感性不高的问题，采用2.3节所述的基于神经网络的补偿方法，采用RBF神经网络，训练数据为正常情况下系统的输入、输出和残差，具体选择时选取不受故障影响或影响相对较小的系统输入输出量来进行补偿模型的构建，可通过合理设置观测器参数矩阵，再通过式(24)，(25)进行校验来调整，选择采用比例阀输入电压，舵机油缸进出口压力值以及正常运行状态下的观测器输出残差进行补偿模型训练构建，采样率为100 Hz.

图12为采用了神经网络补偿模型后的4类故障检测结果.由图可见，所有故障的残差曲线在两个运动方向上均超过了阈值，表明这些早期故障均可得到检测，证明了补偿方法的有效性.此外，采用补偿模型后，启停和速度突变时的残差波动也变小，因此采用固定阈值即可进行故障决策.

图11 故障检测实验结果Fig.11 Experimental fault detection performance without compensation model

图12 采用补偿模型后的故障检测实验结果Fig.12 Experimental fault detection performance with compensation model

4 结语

针对船舶舵机电液伺服系统，提出了一种模型-数据联合驱动的故障诊断方法.建立了系统状态方程和常见故障模型，对系统中的各类不确定因素进行了分类解析并制定了逐层削减策略.系统的不确定参数难以准确测量，采用了基于系统输入输出数据的参数辨识法可进行有效辨识；系统的外负载力未知时变，会干扰早期故障的检测，针对系统的未知时变外干扰及固有非线性，设计了基于系统模型的非线性未知输入观测器，可对系统的非线性进行有效处理并对外干扰进行有效解耦，而不影响对故障的敏感性.系统中的剩余不确定性会影响早期故障的检测，提出了基于神经网络的补偿方法，可以对剩余不确定性的影响进行有效削减，从而提高故障检测的敏感性，仿真和实验结果均说明了该方法的有效性.